智能驾驶规划控制理论学习-基于采样的规划方法
目录
一、基于采样的规划方法概述
二、概率路图(PRM)
1、核心思想
2、实现流程
3、算法描述
4、节点连接处理
5、总结
三、快速搜索随机树(RRT)
1、核心思想
2、实现流程
3、总结
4、改进RRT算法
①快速搜索随机图(RRG)
②基于运动学的快速搜索随机树(Kinematic-based RRT)
一、基于采样的规划方法概述
基于采样的方法就是在状态空间中不断地随机撒点,将这些节点根据一定的规则与周围的节点进行连接,以此构造一条条局部路径,最终找到一条从起点到终点的路径。随着采样点的不断增多,最终得到的解会不断逼近最优解。
一般步骤:
- 为图表添加随机数种子
- 以某种策略或者给定条件采样到起始节点
- 选择和哪些其他节点进行连接
- 选择添加或者移除哪些边
二、概率路图(PRM)
1、核心思想
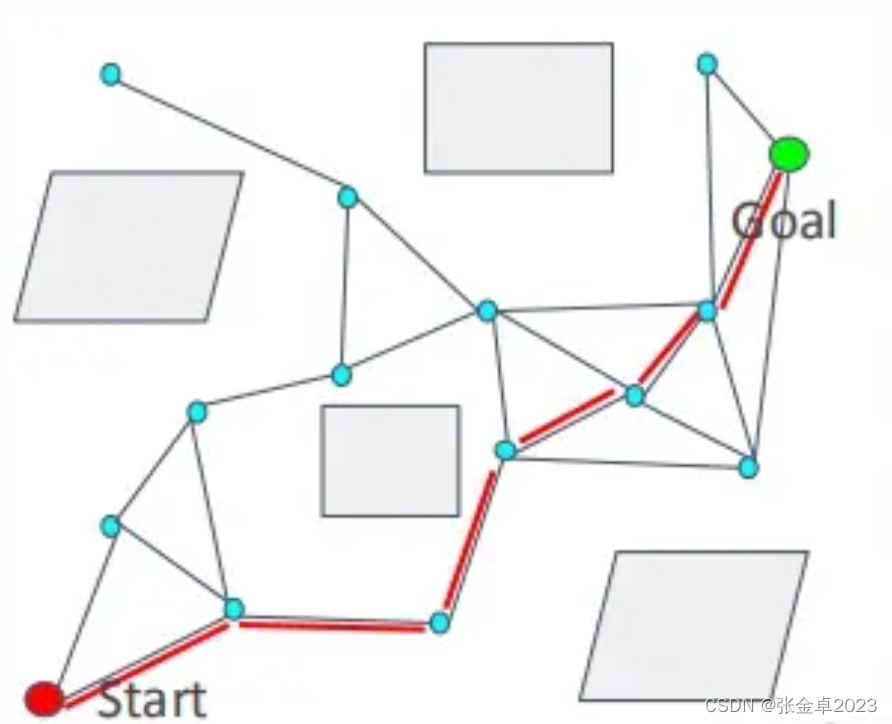
PRM有两个阶段分别是学习阶段(Learning Phase)和查询阶段(Query Phase)。
学习阶段:
- 在配置空间中随机采样足够数量的点;
- 将相互之间能够到达的节点进行连接。
查询阶段:
- 利用图搜索算法寻找图表中从起始节点到目标节点的路径。
2、实现流程

(a)图中所示为一个用于采样的配置空间,在配置空间中,自动驾驶车辆可以被近似看成一个质点,环境中的障碍物等信息都被近似为图中的forbidden space,自动驾驶车辆在free space空间中运动,二无需考虑其几何形状和运动状态;
(b)图中通过随机采样的方式获得一个坐标点,采样的方法也要根据特定的场景做出不同的选择,常见的采样算法有均匀分布采样(在未知场景中采样)、高斯分布采样(在自动驾驶场景中通常以车道中心线为均值)等;

(c)图中通过采样大量的点来获取地图的形状;
(d)图中对采样点进行碰撞检验,删除forbidden space中的采样点;
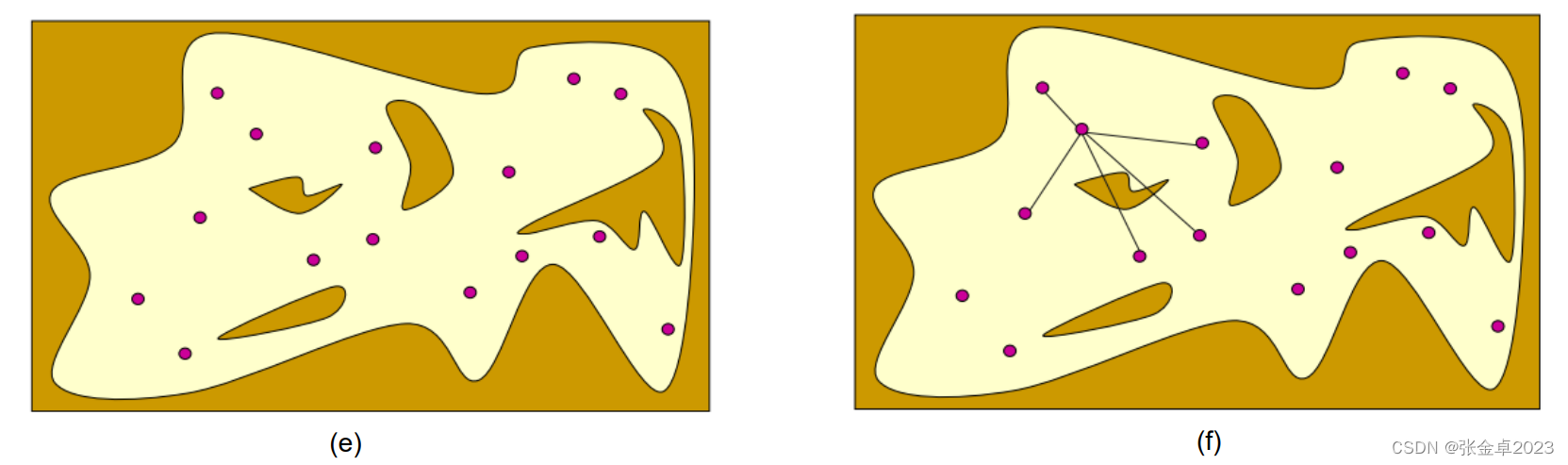
(e)图中为删除forbiden space中的采样点后,在free space中保留下来的有效采样点;
(f)图中每个有效采样点会连接以当前节点为圆心,半径r圆形范围内的所有采样点
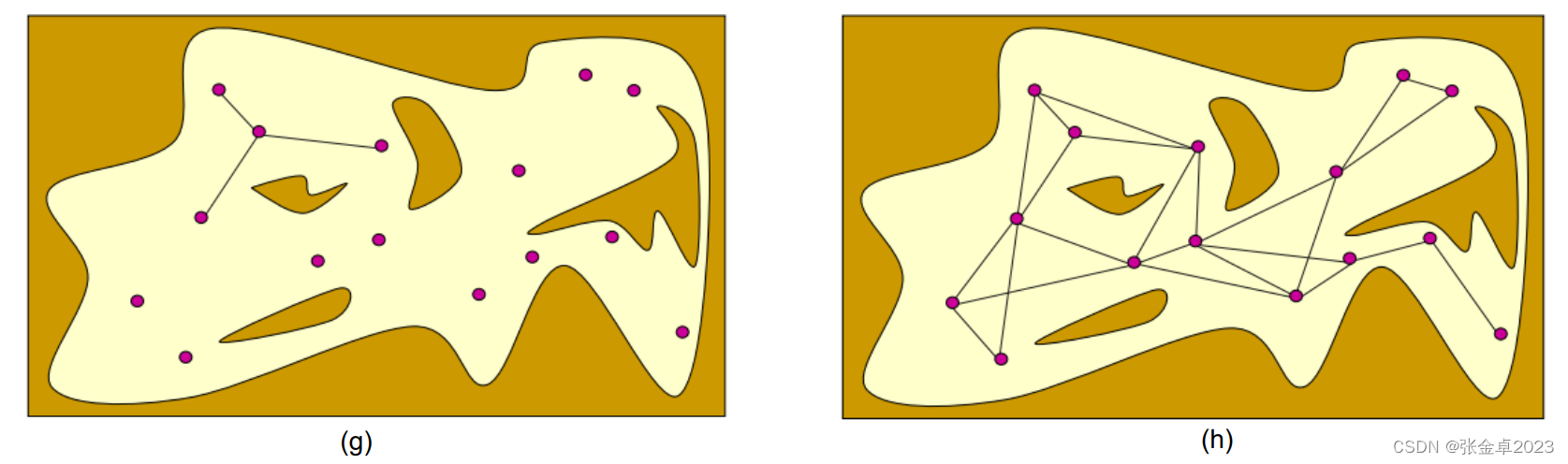 (g)图中若采样点之间的连线与forbiden space相交则发生碰撞,删除发生碰撞的连线;
(g)图中若采样点之间的连线与forbiden space相交则发生碰撞,删除发生碰撞的连线;
(f)图中碰撞检测通过的连线得到保留,作为构成图表graph的边;
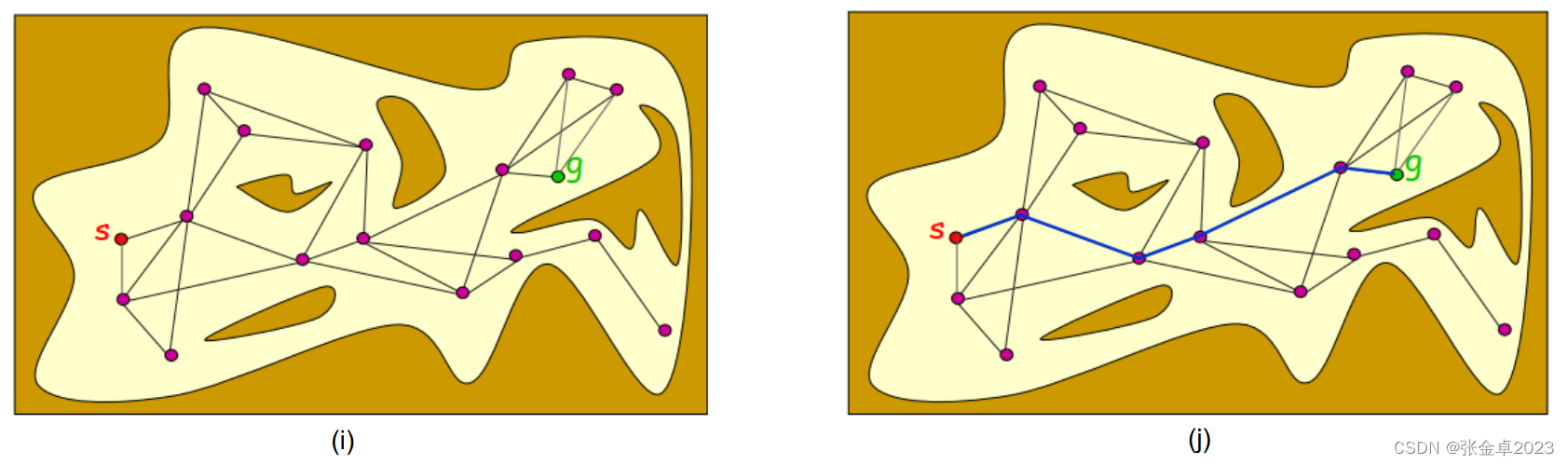
(i)在连线得到的图表graph中添加起始节点和目标节点;
(j)在graph图中利用图搜索算法寻找最优路径。
3、算法描述
用伪代码的方式对PRM进行简要描述:
V <- ∅; E <- ∅ // 分别维护两个集合,一个存放顶点,一个存放边
for i = 0,...,n do //假定最大采样点为n,进入循环x <- SampleFree; //在freespace通过特定的采样策略采样得到一个节点U <- Near(G = (V,E), x, r); //将节点半径r范围内要专注的邻居节点加入集合U中V <- V ∪ {x}; //将当前采样点x加入集合V中,更新集合Vforeach u in U, in order of increasing ||u - x||, do //对集合U中存入的节点进行处理,为了避免节点过于密集,u和x不能过于接近if x and u are not in the same connected component of G = (V,E) then // 保证u和x之间的连线与其他连线不重合if CollisionFree(x,u) then E <- E∪{(x,u),(u,x)}; // 通过碰撞检验则将x和u的连线加入集合E
return G=(V,E); // 返回V和E表示的图上面是经典的PRM算法描述,也可以对其进行简化:
V <- {x}∪{SampleFree}; E <- ∅;
foreach v in V do U <- near(G=(V,E),v,r)\{v};foreach u in U doif CollisionFree(v,u) then E <- E∪{(v,u),(u,v)}
return G=(V,E);主要就是减少了剔除部分节点的步骤,因此在算法实现上效率会降低。
4、节点连接处理
在PRM实现过程中,选择那些节点相连也是需要考虑的问题,下面给出三种可行的方法:
- k-Nearest PRM:选择当前节点最近的k个邻居节点
U ← kNearest(G=(V,E),v,k)
- Bounded-degree PRM:对半径范围内添加的最近节点添加一个边界值k
U ← Near(G,x,r) ∩ kNearest(G=(V,E),v,k)
- Variable-radius PRM:让连接半径称为对应节点个数的函数,而不是固定的参数
5、总结
PRM优点:具有概率完备性,只要采样点足够多,并且生成的图表有解那么一定可以结合图搜索算法找到一条最优解路径;
缺点:
- 如果是连接特定起点和终点,那么通过PRM的两个阶段先建图在搜索是比较浪费资源的;
- 搜索得到的路径是节点之间通过直线连接的,不符合车辆的运动学约束。
三、快速搜索随机树(RRT)
1、核心思想
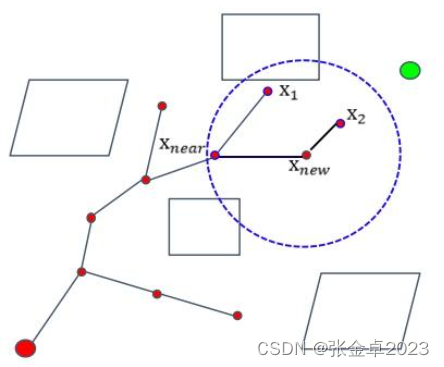
与PRM有学习和查询两个阶段,并且在学习阶段构造的是一个图不同,RRT只有一个阶段,在采样结束的同时就能确定路径,RRT在采样的过程中维护的是一个树结构。相比图描述的网络关系,树结构描述的是一种层次关系。
在RRT算法中,通常将起始节点作为树的根节点,在采样搜索到目标节点时通过回溯就可以确定路径。
2、实现流程
依然使用伪代码对实现流程进行简要描述:
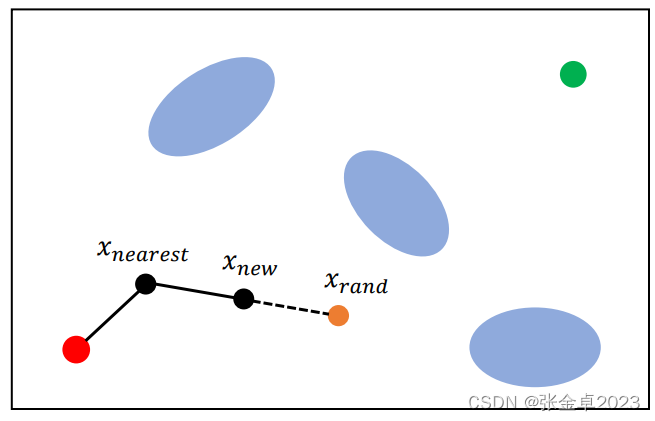
V <- {root}; E <- ∅; // 维护集合V和E,分别存放节点和边,在V中先将初始节点作为根节点放入
for i = 1,...,n doxrand ← SampleFree; // 在freespcace中得到采样点xrandxnearest ← Nearest(G=(V,E),xrand); // 设置离xrand距离最近的树节点为xnearestxnew ← steer(xnearest,xrand); // 通过特定的方式将xnearest与xrand进行连接,此处直接设置了一个中间节点,比较经典的方式设置一段弧长if ObtacleFree(xnearest,xrand) then // 进行连线障碍物检测V ← V∪{xnew}; E ← E∪{xnearest,xnew}; // 检测通过将边保存到集合E中
return G={V,E};

3、总结
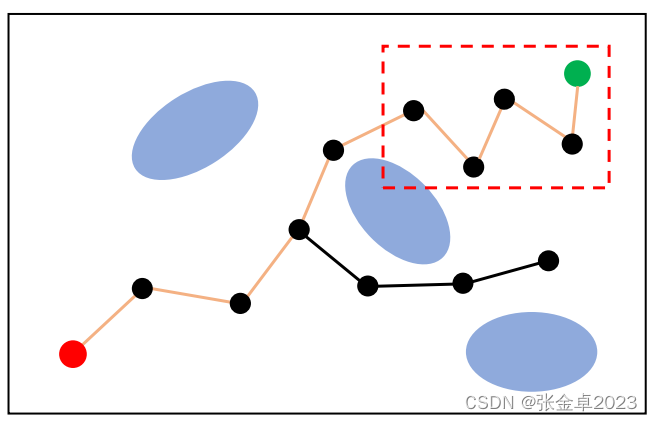
优点:如果是找寻找两个特定节点间的路径,RRT的效率会显著地优于PRM;
缺点:RRT不具备概率完备性,因为它每次都是树的最近节点连接,如下图红色区域中搜索得到的路径显然不是最优解。
4、改进RRT算法
为了解决RRT算法不具备概率完备性的缺陷,后来又提出了多种改进的RRT算法。
①快速搜索随机图(RRG)
V <- {root}; E <- ∅;
for i = 1,...,n doxrand ← SampleFree; xnearest ← Nearest(G=(V,E),xrand); xnew ← steer(xnearest,xrand);if ObtacleFree(xnearest,xrand) then Xnear ← Near(G=(V,E),xnew,min{γRRG(log(card(V))/card(V)^(1/d),η); // 将xnew附近给定半径内的所有节点都存入Xnear集合中V ← V∪{xnew}; E ← E∪{xnearest,xnew};foreach xnear in Xnear doif CollisionFree(xnear,xnew) then E ← E∪{xnearest,xnew}; // 将通过碰撞检测的所有Xnear集合中的节点与xnew的连线都存入集合E中return G={V,E};核心思想:不仅仅只是连接xnew和xnearest,将xnew半径范围内的所有符合非碰撞条件的节点都连接。
虽然RRG使得算法具有概率完备性,但是却违背了RRT算法提高效率的初衷,因为RRG算法在实现过程中并没有在维护树结构,输出的依然是一个图,相当于是PRM的学习阶段,还要再利用搜索算法进行最优路径确定。
②基于运动学的快速搜索随机树(Kinematic-based RRT)
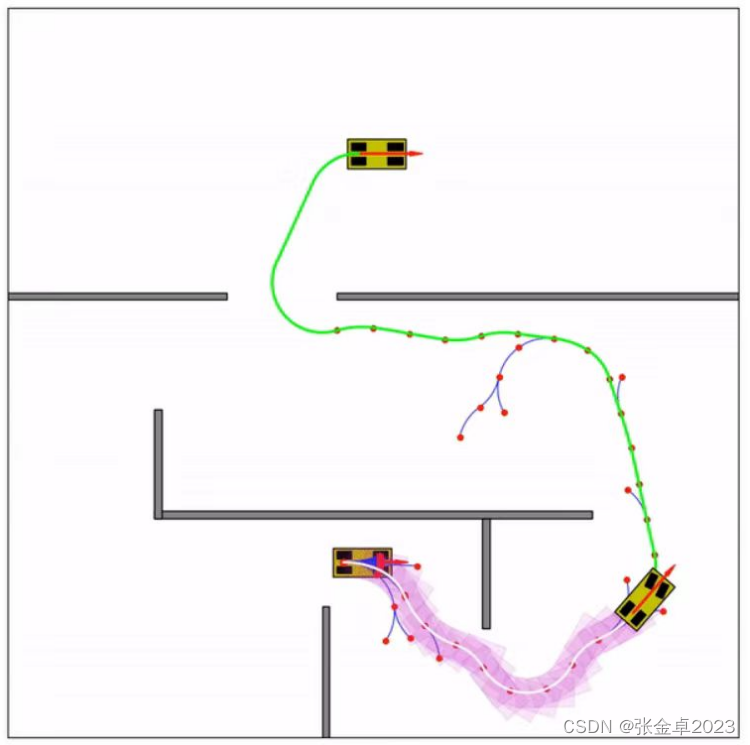
核心思想:利用车辆运动学方法在两个节点之间进行转向,主要在于RRT伪代码中xnew获取步骤的优化。
上图所示是基于杜宾斯规划(dubins_path_planning)得到的路径,可以看出在引入车辆运动学方法后,得到的最终路径是一条较为平滑的曲线。dubins_path_planning的具体介绍在后面会具体介绍。
相关文章:

智能驾驶规划控制理论学习-基于采样的规划方法
目录 一、基于采样的规划方法概述 二、概率路图(PRM) 1、核心思想 2、实现流程 3、算法描述 4、节点连接处理 5、总结 三、快速搜索随机树(RRT) 1、核心思想 2、实现流程 3、总结 4、改进RRT算法 ①快速搜索随机图&a…...
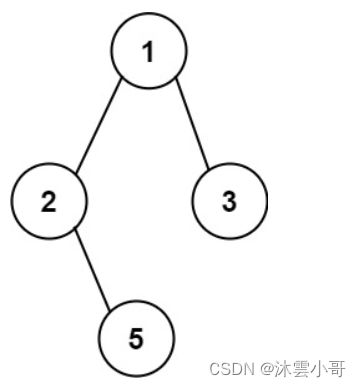
二叉树——二叉树所有路径
二叉树所有路径 给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。 叶子节点 是指没有子节点的节点。 示例 1: 输入:root [1,2,3,null,5] 输出:["1->2->5","1-…...
,动态规划6)
算法训练营day38(补),动态规划6
package main func max(a, b int) int { if a > b { return a } return b } 背包最大重量为4。 物品为: 重量价值物品0115物品1320物品2430 每件商品都有无限个! 问背包能背的物品最大价值是多少? func package03(weight, value []…...

【java、微服务、nacos】nacos服务分级存储模型
Nacos服务分级存储模型 ① 一级是服务,例如userservice ②二级是集群,例如杭州或上海 ③ 三级是实例,例如杭州机房的某台部署了userservice的服务器 配置实例集群属性 改变服务的yml文件 spring:cloud:nacos:discovery:cluster-name: H…...

共享旅游卡:打开0费用旅游新纪元,探索40+精彩线路
随着现代生活节奏的加快,旅游成为了许多人释放压力、寻求乐趣的方式。然而,面对琳琅满目的旅游线路和不断上涨的旅游费用,许多人望而却步。 今天,我们要为您介绍一种颠覆传统旅游方式的创新产品——共享旅游卡。它不仅能让您以0费…...
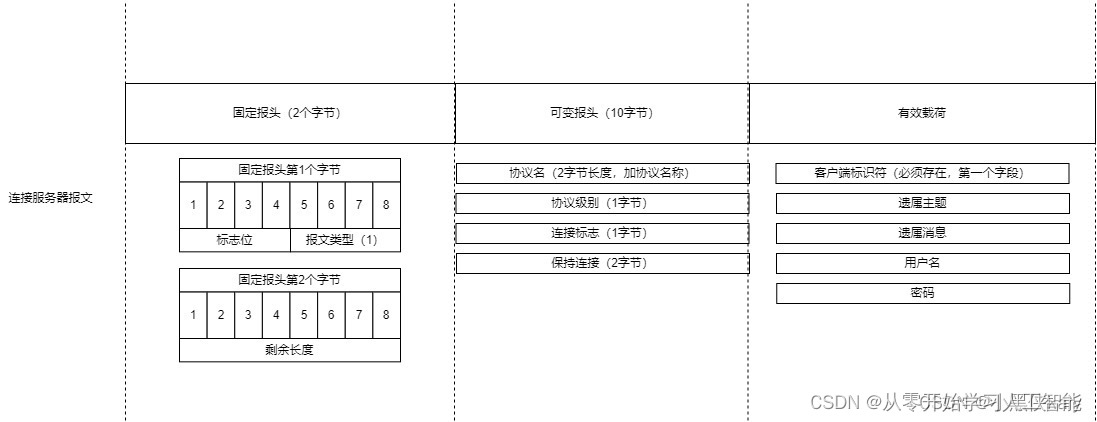
MQTT协议解析:揭秘固定报头、可变报头与有效载荷的奥秘
MQTT(Message Queuing Telemetry Transport,消息队列遥测传输协议)是一种轻量级的通讯协议,常用于远程传感器和控制设备的通讯。MQTT协议基于发布/订阅模式,为大量计算能力有限且工作在低带宽、不可靠网络环境中的设备…...
备战蓝桥杯---树形DP基础3
上一次我们讲了二叉苹果树,现在我们加一点难度,从二叉变成了多叉苹果树。 这样子我们就不可以直接按照上次的方法DP,我们其实可以发现,我们可以用类似背包的思想求解,这就是所谓的树上背包。 我们先加进第一个儿子来…...
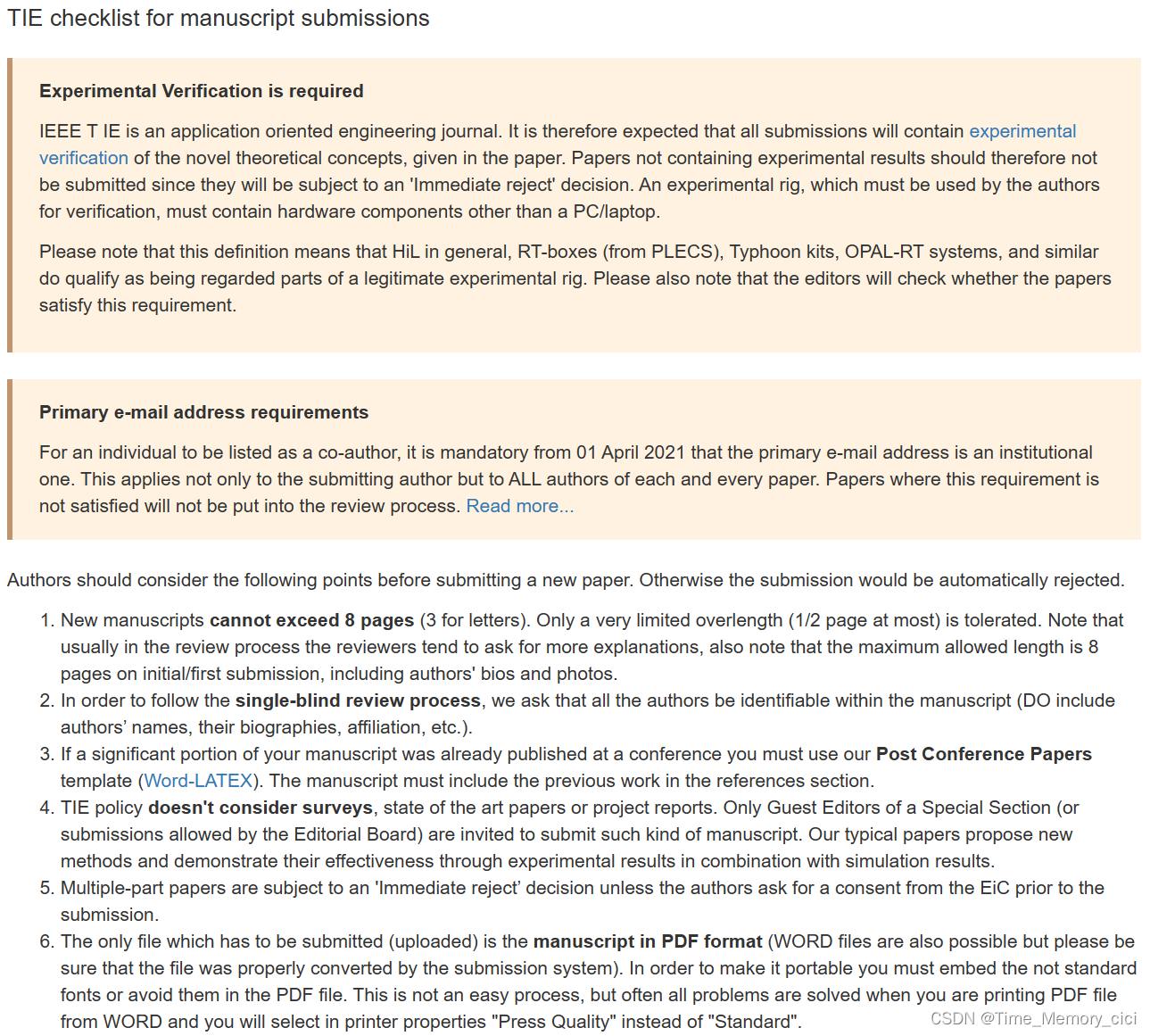
IEEE Transactions on Industrial Electronics工业电子TIE修改稿注意事项及提交须知
一、背景 兔年末投了一篇TIE,手稿初次提交的注意事项也整理成了博客IEEE Transactions on Industrial Electronics工业电子TIE论文投稿须知,获得了许多点赞和收藏。最近也收到了审稿结果,给的意见是大修major revision,总之只要不…...

c#委托的三种实现方式
委托是实质一个类,主要目的是将方法当作参数进行传递。 委托是.NET编程的精髓之一,在日常编程中经常用到,在C#中实现委托主要有Func、Action、delegate三种方式,本节主要就这三种委托的用法通过实例展开讲解。 Func用法解析 【F…...

c/c++|红黑树|分析应用|锚点
红黑树是一种自平衡的二叉查找树,它保持着良好的平衡,能够在插入和删除等操作后通过一系列旋转和重新着色操作来保持树的平衡。这种平衡性质使得红黑树在搜索、插入和删除等操作的平均和最坏情况下的时间复杂度都是O(log n)。以下是红黑树的一些关键特性…...

2-29算法习题总结
贪心问题 小A的糖果 题目描述 小 A 有 n n n 个糖果盒,第 i i i 个盒中有 a i a_i ai 颗糖果。 小 A 每次可以从其中一盒糖果中吃掉一颗,他想知道,要让任意两个相邻的盒子中糖的个数之和都不大于 x x x,至少得吃掉几颗糖…...

当Linux 磁盘满了,查看大文件并删除
当你的Linux磁盘空间满了时,可以通过以下步骤查找大文件并删除它们: 检查磁盘空间: 使用以下命令检查磁盘空间的使用情况: df -h这将显示文件系统的使用情况,包括每个文件系统的总大小、已用空间、可用空间和挂载点。 …...

STL -萃取特性迭代器
1. STL简单概述 a. STL六大组成部分 容器(Container)空间配置器(allocator)算法(Algorithm)迭代器(Iterator)仿函数(Function object)适配器(Ad…...

python pandas写入csv
在Python的Pandas库中,可以使用to_csv方法将DataFrame对象写入CSV文件。以下是一个简单的示例: import pandas as pd# 创建一个DataFrame对象 data {Name: [Alice, Bob, Charlie, David],Age: [25, 30, 35, 40],City: [New York, Los Angeles, Chicago…...

oracle 数据库建集群式数据库的DBLINK的语法
根据需要修改以下红色字体的部分即可。 1、连接集群式数据库DBLINK语法 create public database link 自定义的dblink名字 connect to 连接对方数据库的用户名 identified by "密码" using (DESCRIPTION (ADDRESS_LIST (FAILOVER ON) (LOAD_BALANCE OFF) …...

基于JAVA的毕业设计分配选题系统 开源项目
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 专业档案模块2.2 学生选题模块2.3 教师放题模块2.4 选题审核模块 三、系统展示四、核心代码4.1 查询专业4.2 新增专业4.3 选择课题4.4 取消选择课题4.5 审核课题 五、免责说明 一、摘要 1.1 项目介绍 基于JAVAVueSpri…...

Android 接入指纹识别
接入指纹框架:https://github.com/Tencent/soter implementation com.github.Tencent.soter:soter-wrapper:2.0.91.Application中初始化 class IApplication : Application() {override fun onCreate() {super.onCreate()instance thisinitSort()}private fun in…...

如何通过代理IP安全使用Linkedln领英?
LinkedIn是跨境外贸必备的拓客工具,世界各地的许多专业人士都使用领英来作为发布和共享内容的主要工具,这使得它成为跨境出海必备的渠道工具。 但是不少做外贸的朋友都知道,领英账号很容易遭遇限制封禁,但如果善用工具࿰…...

嵌入式驱动学习第一周——定时器与延时函数
前言 这篇博客一起学习定时器,定时器是最常用到的功能之一,其最大的作用之一就是提供了延时函数。 嵌入式驱动学习专栏将详细记录博主学习驱动的详细过程,未来预计四个月将高强度更新本专栏,喜欢的可以关注本博主并订阅本专栏&…...

Tips杂记
🥲 🥸 🤌 🫀 🫁 🥷 🐻❄️🦤 🪶 🦭 🪲 🪳 🪰 🪱 🪴 🫐 🫒 🫑…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...
