c#委托的三种实现方式
委托是实质一个类,主要目的是将方法当作参数进行传递。
委托是.NET编程的精髓之一,在日常编程中经常用到,在C#中实现委托主要有Func、Action、delegate三种方式,本节主要就这三种委托的用法通过实例展开讲解。
Func用法解析
【Func】:Func是带返回值的委托:
原型函数如下(以下展示的是有两个参数的情况):
public delegate TResult Func<in T1, in T2, out TResult>(T1 arg1, T2 arg2);用法举例1: 定义方法StringAddA
public int StringAddA(string a, string b){return int.Parse(a) + int.Parse(b);}
定义委托func,然后把方法StringAddA委托给它,接下来执行委托并获取结果,注意:
Func<string, string, int> func = StringAddA;是Func<string, string, int> func = new Func<string, string, int>(StringAddA);的简写
Func<string, string, int> func = StringAddA;//简写var result = func.Invoke("3", "5");//可以简化为func("3", "5")sw.AppendLine($"【func用法1】func返回结果是:{result}");
这里的执行结果是: 【func用法1】func返回结果是:8
用法举例2:
用lamda表达式简化写法,通过+=注册实现多播委托
func += (a, b) =>{return int.Parse(a) - int.Parse(b);};sw.AppendLine($"【func用法2】func返回结果是:{func("3", "5")}");
这里的执行结果是: 【func用法1】func返回结果是:-2
注意 += 可以注册多个委托,委托执行后会按顺序执行方法.
Action用法解析
【Action】:Action是无返回值的委托:
原型函数如下(以下展示的是有两个参数的情况):
public delegate void Action<in T1, in T2>(T1 arg1, T2 arg2);用法举例:
先定义方法:StringAddB
public void StringAddB(string a, string b){sw.AppendLine($"【Action用法】Action执行结果:{(int.Parse(a) + int.Parse(b))}");}
实例如下:
Action<string, string> action = StringAddB;//简写IAsyncResult asyncResult = action.BeginInvoke("3", "5", null, null);//action("3", "5"),BeginInvoke异步执行,即:开启新现成处理StringAddBaction.EndInvoke(asyncResult);//阻塞委托,直到执行完成if (asyncResult.IsCompleted){sw.AppendLine($"【Action用法】当前异步委托线程已执行完成");}
这里BeginInvoke是异步委托,即新开线程去处理,我们的窗体线程在1号线程,这里我们可以在StringAddB里面打印线程id号
sw.AppendLine($"【Action用法】Action执行线程id:{Thread.CurrentThread.ManagedThreadId}");运行结果:
【Action用法】Action执行线程id:3
这里的EndInvoke是阻塞委托,直到执行完成,当然我们这里也可以用同步的Invoke去执行,甚至Invoke都可以简写去掉,直接写成action("3", "5")
delegate用法解析
【delegate】:delegate是可以有返回值也可以没返回值的委托:
使用前需要先声明:
delegate int DelegateM(string a, string b);//声明,可以有返回值也可以没有用法举例:
//delegate用法//DelegateM delegateM = new DelegateM(p.StringAddA);DelegateM delegateM = StringAddA;//简写sw.AppendLine($"【delegate用法】delegate返回结果是:{delegateM("3", "5")}");
以上就是三种委托的区别和用法讲解,那使用委托最大的优势是什么:
可以将方法当作参数去传递,用法举例如下:
Test(func, action);//将方法委托后转化为参数进行传递定义方法
public void Test(Func<string, string, int> f, Action<string, string> a){a.Invoke(f.Invoke("3", "5").ToString(), "5");}
都看到这了,如果您感觉我推荐的内容对您有帮助,希望您能伸出援手,给我打赏一元请我喝瓶水;您的支持将是我在继续分享传作路上的无限动力。如果您囊肿羞涩也没有关系,希望您多写评论予以支持,山高水常,来日在见。
相关文章:

c#委托的三种实现方式
委托是实质一个类,主要目的是将方法当作参数进行传递。 委托是.NET编程的精髓之一,在日常编程中经常用到,在C#中实现委托主要有Func、Action、delegate三种方式,本节主要就这三种委托的用法通过实例展开讲解。 Func用法解析 【F…...

c/c++|红黑树|分析应用|锚点
红黑树是一种自平衡的二叉查找树,它保持着良好的平衡,能够在插入和删除等操作后通过一系列旋转和重新着色操作来保持树的平衡。这种平衡性质使得红黑树在搜索、插入和删除等操作的平均和最坏情况下的时间复杂度都是O(log n)。以下是红黑树的一些关键特性…...

2-29算法习题总结
贪心问题 小A的糖果 题目描述 小 A 有 n n n 个糖果盒,第 i i i 个盒中有 a i a_i ai 颗糖果。 小 A 每次可以从其中一盒糖果中吃掉一颗,他想知道,要让任意两个相邻的盒子中糖的个数之和都不大于 x x x,至少得吃掉几颗糖…...

当Linux 磁盘满了,查看大文件并删除
当你的Linux磁盘空间满了时,可以通过以下步骤查找大文件并删除它们: 检查磁盘空间: 使用以下命令检查磁盘空间的使用情况: df -h这将显示文件系统的使用情况,包括每个文件系统的总大小、已用空间、可用空间和挂载点。 …...

STL -萃取特性迭代器
1. STL简单概述 a. STL六大组成部分 容器(Container)空间配置器(allocator)算法(Algorithm)迭代器(Iterator)仿函数(Function object)适配器(Ad…...

python pandas写入csv
在Python的Pandas库中,可以使用to_csv方法将DataFrame对象写入CSV文件。以下是一个简单的示例: import pandas as pd# 创建一个DataFrame对象 data {Name: [Alice, Bob, Charlie, David],Age: [25, 30, 35, 40],City: [New York, Los Angeles, Chicago…...

oracle 数据库建集群式数据库的DBLINK的语法
根据需要修改以下红色字体的部分即可。 1、连接集群式数据库DBLINK语法 create public database link 自定义的dblink名字 connect to 连接对方数据库的用户名 identified by "密码" using (DESCRIPTION (ADDRESS_LIST (FAILOVER ON) (LOAD_BALANCE OFF) …...

基于JAVA的毕业设计分配选题系统 开源项目
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 专业档案模块2.2 学生选题模块2.3 教师放题模块2.4 选题审核模块 三、系统展示四、核心代码4.1 查询专业4.2 新增专业4.3 选择课题4.4 取消选择课题4.5 审核课题 五、免责说明 一、摘要 1.1 项目介绍 基于JAVAVueSpri…...

Android 接入指纹识别
接入指纹框架:https://github.com/Tencent/soter implementation com.github.Tencent.soter:soter-wrapper:2.0.91.Application中初始化 class IApplication : Application() {override fun onCreate() {super.onCreate()instance thisinitSort()}private fun in…...

如何通过代理IP安全使用Linkedln领英?
LinkedIn是跨境外贸必备的拓客工具,世界各地的许多专业人士都使用领英来作为发布和共享内容的主要工具,这使得它成为跨境出海必备的渠道工具。 但是不少做外贸的朋友都知道,领英账号很容易遭遇限制封禁,但如果善用工具࿰…...

嵌入式驱动学习第一周——定时器与延时函数
前言 这篇博客一起学习定时器,定时器是最常用到的功能之一,其最大的作用之一就是提供了延时函数。 嵌入式驱动学习专栏将详细记录博主学习驱动的详细过程,未来预计四个月将高强度更新本专栏,喜欢的可以关注本博主并订阅本专栏&…...

Tips杂记
🥲 🥸 🤌 🫀 🫁 🥷 🐻❄️🦤 🪶 🦭 🪲 🪳 🪰 🪱 🪴 🫐 🫒 🫑…...

可以用numpy为for加速
Numpy除了用于科学计算,还有一个功能是可以代替某些for循环,进行同样的功能实现,有于是向量矩阵运算,碰到复杂的for时,计算速度可以提高,从而提高程序性能。以下是一些常用的NumPy函数和操作,可…...

cartographer ceres后端优化
这里引用一篇文章 https://zhuanlan.zhihu.com/p/567635409 因为cartographer中的代码有的地方添加了AddParameterBlock,有的地方没有添加,会引起歧义,原来AddParameterBlock可以隐式添加优化变量,这篇文章介绍了具体原因,核心内容如下: AddParameterBlock的作用作用一:…...
day57 集合 List Set Map
List实现类 List接口特点:元素有序 可重复 Arraylist 可变数组 jdk 8 以前Arraylist容量初始值10 jdk8 之后初始值为0,添加数据时,容量为10; ArrayList与Vector的区别? LinkList:双向链表 优点࿱…...

蓝桥杯:真题讲解3(C++版)附带解析
报纸页数 来自:2016年七届省赛大学C组真题(共8道题) 分析: --画出报纸长的样子,如果我们在上面多画一张报纸,那么就符合题意的5,6,11,12。 观察这张图:观察3…...
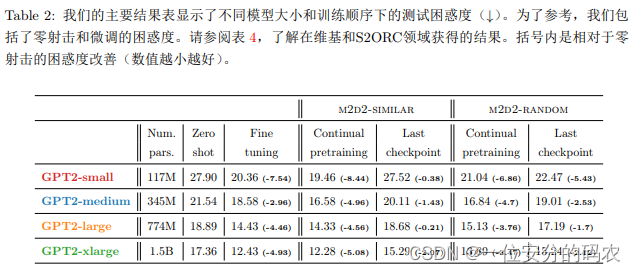
继续预训练对大语言模型的影响
翻译自文章:Investigating Continual Pretraining in Large Language Models: Insights and Implications 摘要 本文研究了大型语言模型(LLMs)中不断学习(CL)的不断发展领域,重点是制定有效和可持续的训练…...

关于空频变换的知识点
1.DCT变换: 离散余弦变换是一种将图像从空域转换到频域的技术,它可以将图像分解为频域分量。对于RGB图像,它由红色(R)、绿色(G)和蓝色(B)三个通道组成。当应用DCT变换时…...

纯css实现-让字符串在文字少时显示为居中对齐,而在文字多时显示为左对齐
纯css实现-让字符串在文字少时显示为居中对齐,而在文字多时显示为左对齐 使用flex实现 思路 容器样式(.container): Flex容器的BFC性质使得其内部的子元素(.text-box)在水平方向上能够居中,通过justify-c…...
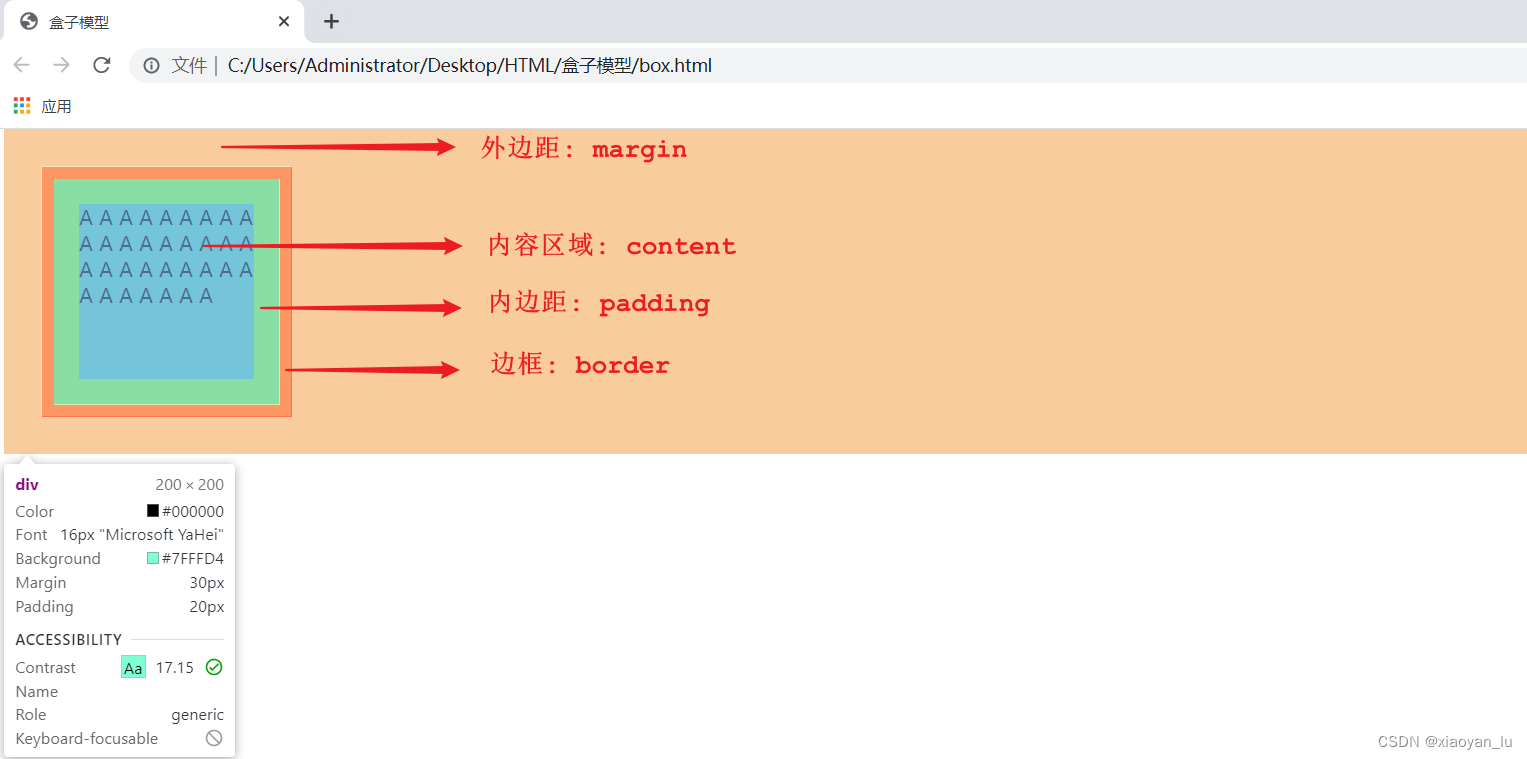
初学HTMLCSS——盒子模型
盒子模型 盒子:页面中所有的元素(标签),都可以看做是一个 盒子,由盒子将页面中的元素包含在一个矩形区域内,通过盒子的视角更方便的进行页面布局盒子模型组成:内容区域(content&…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
