代码随想录算法训练营第四十七天丨198. 打家劫舍、 213. 打家劫舍 II、337. 打家劫舍 III
198. 打家劫舍
自己的思路:
初始化两个dp数组,dp[i][0]表示不偷第i户,在0-i户可以偷到的最大金额,dp[i][1]表示偷i户在0-i户可以偷到的最大金额。
class Solution:def rob(self, nums: List[int]) -> int:n = len(nums)dp = [[0] * 2 for _ in range(n)]dp[0][1] = nums[0]for i in range(1, n):dp[i][0] = max(dp[i - 1][0], dp[i - 1][1])dp[i][1] = dp[i - 1][0] + nums[i]return max(dp[n - 1][0], dp[n - 1][1])优化:
有一点臃肿,可以优化。dp[i][1]实际上跟dp[i-1][1]就没啥关系,直接把dp数组初始化成一维的就行了。
class Solution:def rob(self, nums: List[int]) -> int:n = len(nums)if n == 1:return nums[0]if n == 2:return max(nums[0], nums[1])dp = [0] * ndp[0] = nums[0]dp[1] = max(nums[0], nums[1])for i in range(2, n):dp[i] = max(dp[i - 1], dp[i - 2] + nums[i])return dp[n - 1]更优化:
想起了斐波那契数列...
class Solution:def rob(self, nums: List[int]) -> int:n = len(nums)if n == 1:return nums[0]if n == 2:return max(nums[0], nums[1])prev = nums[0]cur = max(nums[0], nums[1])for i in range(2, n):prev, cur = cur, max(cur, prev + nums[i])return cur213. 打家劫舍 II
还是比较容易想到的,把环展成两个线性的,一个去头一个去尾即可。
class Solution:def rob(self, nums: List[int]) -> int:n = len(nums)if n == 1:return nums[0]if n == 2:return max(nums[0], nums[1])def helper(n, nums):dp = [0] * ndp[0] = nums[0]dp[1] = max(nums[0], nums[1])for i in range(2, n):dp[i] = max(dp[i - 1], dp[i - 2] + nums[i])return dp[n - 1]return max(helper(n-1, nums[1:]), helper(n-1, nums[:-1]))337. 打家劫舍 III
我的思路:
有点类似贪心的最后一题。
一顿操作AC了,中间遗漏了几种情况,修改后正确了。
class Solution:def rob(self, root: Optional[TreeNode]) -> int:def helper(root):if not root.left and not root.right:return 0, root.valelif root.left and root.right:left_without_self, left_with_self = helper(root.left)right_without_self, right_with_self = helper(root.right)return max(left_without_self + right_without_self, left_with_self + right_with_self, left_without_self + right_with_self, left_with_self + right_without_self), left_without_self + right_without_self + root.valelif root.left and not root.right:left_without_self, left_with_self = helper(root.left)return max(left_with_self, left_without_self), left_without_self + root.valelif root.right and not root.left:right_without_self, right_with_self = helper(root.right)return max(right_with_self, right_without_self), right_without_self + root.valreturn max(helper(root))优化:
终止条件从叶子节点改成空节点,可以将之后的情况全部统一起来。
class Solution:def rob(self, root: Optional[TreeNode]) -> int:def helper(root):if not root:return 0, 0left = helper(root.left)right = helper(root.right)not_include = max(left) + max(right)include = left[0] + right[0] + root.valreturn not_include, includereturn max(helper(root))带备忘的递归:
class Solution:def rob(self, root: Optional[TreeNode]) -> int:memo = {}def helper(node):if not node:return 0if node in memo:return memo[node]val = node.val# 如果偷当前节点,则不能偷其直接的左右子节点,但可以偷其孙子节点if node.left:val += helper(node.left.left) + helper(node.left.right)if node.right:val += helper(node.right.left) + helper(node.right.right)# 不偷当前节点,可以偷其左右子节点not_steal = helper(node.left) + helper(node.right)# 对于当前节点,选择偷与不偷的最大值result = max(val, not_steal)memo[node] = resultreturn resultreturn helper(root)今日总结:
自己写能AC,都能get到要点~~~精简的代码还是得看题解。
相关文章:

代码随想录算法训练营第四十七天丨198. 打家劫舍、 213. 打家劫舍 II、337. 打家劫舍 III
198. 打家劫舍 自己的思路: 初始化两个dp数组,dp[i][0]表示不偷第i户,在0-i户可以偷到的最大金额,dp[i][1]表示偷i户在0-i户可以偷到的最大金额。 class Solution:def rob(self, nums: List[int]) -> int:n len(nums)dp […...

龙蜥Anolis 8.4 anck 安装mysql5.7
el8没有用mysql5.7了,镜像里是mysql8。 禁用 sudo dnf remove mysql sudo dnf module reset mysql sudo dnf module disable mysql 修改Yum源 sudo vi /etc/yum.repos.d/mysql-community.repo [mysql57-community] nameMySQL 5.7 Community Server baseurlhttp:…...

【踩坑】修复xrdp无法关闭Authentication Required验证窗口
转载请注明出处:小锋学长生活大爆炸[xfxuezhang.cn] 问题如下,时不时出现,有时还怎么都关不掉,很烦: 解决方法一:命令行输入 dbus-send --typemethod_call --destorg.gnome.Shell /org/gnome/Shell org.gn…...

python学习笔记 - 标准库常量
Python 中有一些内置的常量,它们是一些特殊的值,通常不会改变。以下是其中一些常见的内置常量及其详细解释以及使用示例: True: 表示布尔值真。给 True 赋值是非法的并会引发 SyntaxError。 x True print(x) # 输出:…...
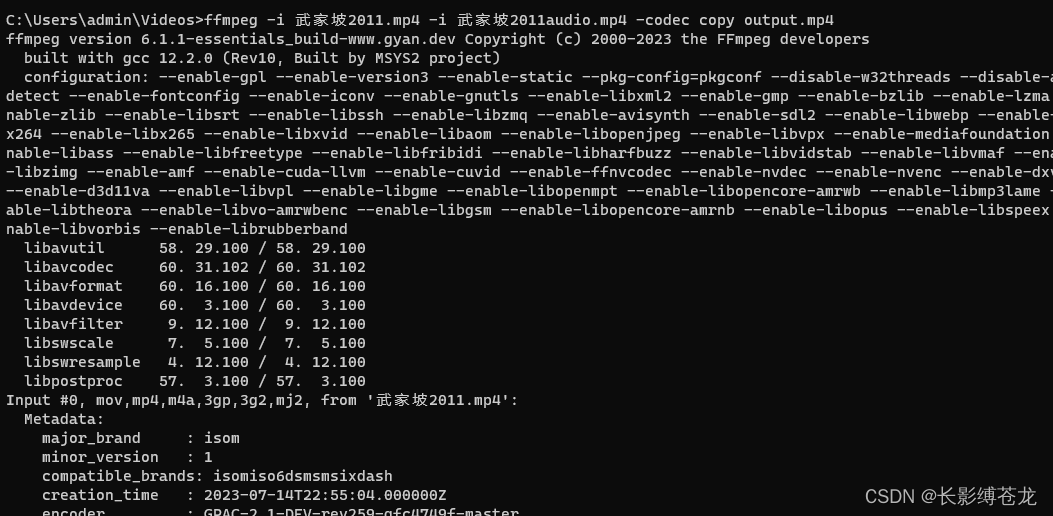
视频和音频使用ffmpeg进行合并和分离(MP4)
1.下载ffmpeg 官网地址:https://ffmpeg.org/download.html 2.配置环境变量 此电脑右键点击 属性 - 高级系统配置 -高级 -环境变量 - 系统变量 path 新增 文件的bin路径 3.验证配置成功 ffmpeg -version 返回版本信息说明配置成功4.执行合并 ffmpeg -i 武家坡20…...
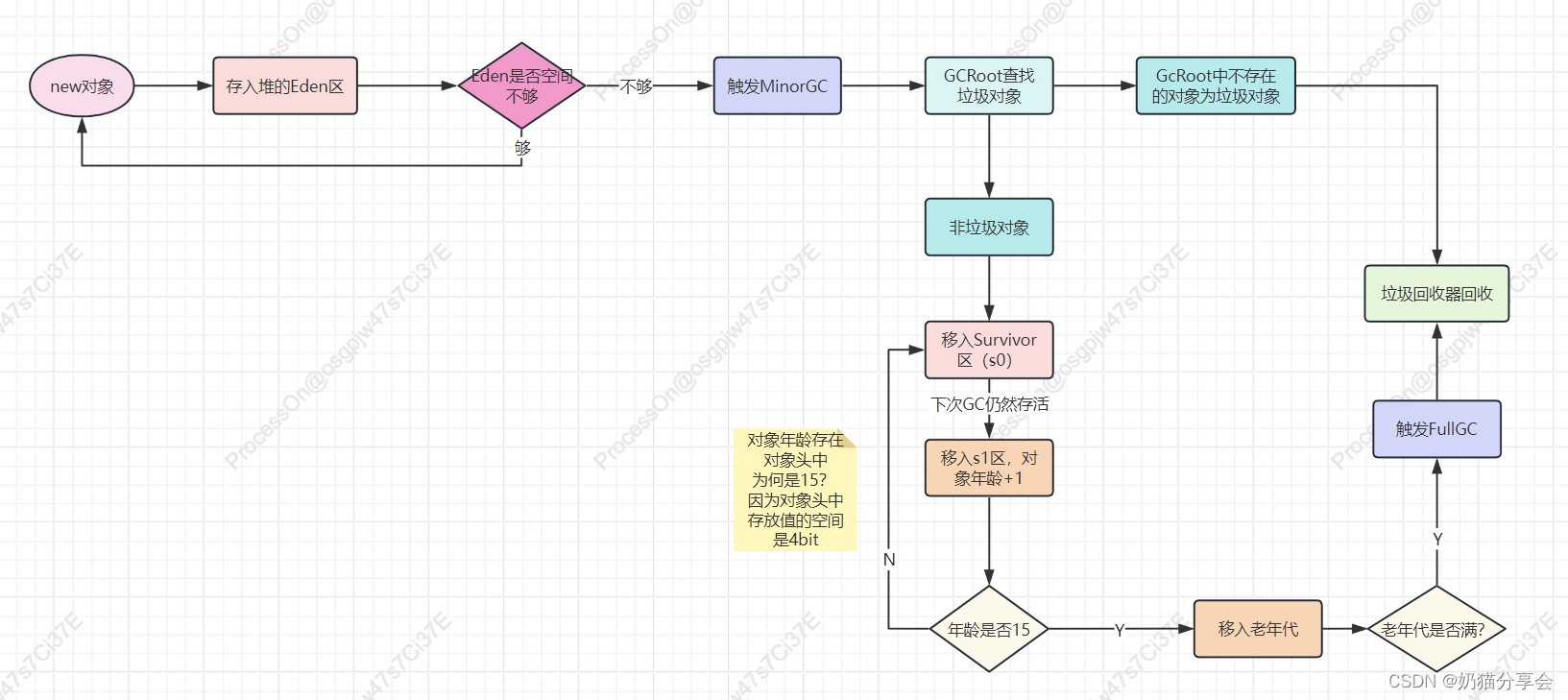
02| JVM堆中垃圾回收的大致过程
如果一直在创建对象,堆中年轻代中Eden区会逐渐放满,如果Eden放满,会触发minor GC回收,创建对象的时GC Roots,如果存在于里面的对象,则被视为非垃圾对象,不会被此次gc回收,就会被移入…...

R语言数据可视化之美专业图表绘制指南(增强版):第1章 R语言编程与绘图基础
第1章 R语言编程与绘图基础 目录 第1章 R语言编程与绘图基础前言1.1 学术图表的基本概念1.1.1 学术图表的基本作用1.1.2基本类别1.1.3 学术图表的绘制原则 1.2 你为什么要选择R1.3 安装 前言 这是我第一次在博客里展示学习中国作者的教材的笔记。我选择这本书的依据是作者同时…...
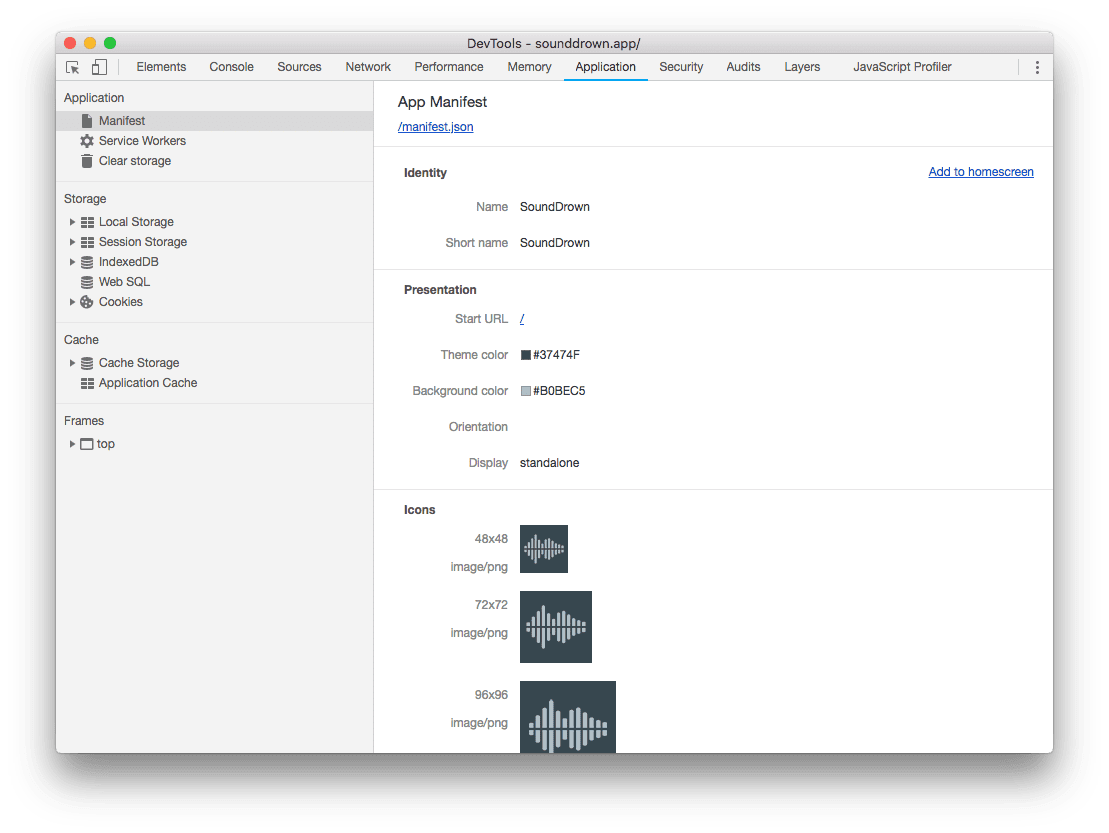
网站添加pwa操作和配置manifest.json后,没有效果排查问题
pwa技术官网:https://web.dev/learn/pwa 应用清单manifest.json文件字段说明:https://web.dev/articles/add-manifest?hlzh-cn Web App Manifest:Web App Manifest | MDN 当网站添加了manifest.json文件后,也引入到html中了&a…...

MongoDB聚合运算符:$cosh
文章目录 语法使用举例双曲余弦值角度双曲余弦值弧度 $cosh聚合运算符用来计算双曲余弦值,返回指定表达式的双曲余弦值。 语法 { $cosh: <expression> }<expression>为可被解析为数值的表达式$cosh返回弧度,使用$radiansToDegrees运算符可…...

Jenkins配置在远程服务器上执行shell脚本(两种方式)
Jenkins配置在远程服务器上执行shell脚本 方式一:通过SSH免密方式执行 说明:Jenkins部署在ServerA:10.1.1.74上,要运行的程序在ServerB:10.1.1.196 分两步 第一步:Linux Centos7配置SSH免密登录 Linux…...

Java+SpringBoot,打造社区疫情信息新生态
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…...

js ES6判断字符串是否以某个字符串开头或者结尾startsWith、endsWith
1.前言 startsWith:startsWith方法用于检查字符串是否以指定的字符串开头。 endsWith:endsWith方法用于检查字符串是否以指定的字符串结尾。 2.用法示例 const str Hello, world!;console.log(str.startsWith(Hello)); // true console.log(str.starts…...

Bert-as-service 实战
参考:bert-as-service 详细使用指南写给初学者-CSDN博客 GitHub - ymcui/Chinese-BERT-wwm: Pre-Training with Whole Word Masking for Chinese BERT(中文BERT-wwm系列模型) 下载:https://storage.googleapis.com/bert_models/…...
微信小程序(四十七)多个token存储
注释很详细,直接上代码 新增内容: 1.基础存储模板 2.中括号实现变量名匹配 源码: app.js App({//提前声明的变量名token:wx.getStorageSync(toke),refreshToken:wx.getSystemInfoAsync(refreshToken),setToken(key,token){//保存token到全局…...

机器学习(II)--样本不平衡
现实中,样本(类别)样本不平衡(class-imbalance)是一种常见的现象,如:金融欺诈交易检测,欺诈交易的订单样本通常是占总交易数量的极少部分,而且对于有些任务而言少数样本更…...

几个好用的 VUE Table
Vue easytable - 功能恰到好处 无学习成本 上手就用Vue good table - UI 清新 功能直给 适合小项目Vxe table - 宝藏级 table 组件 高级功能低调好用 维护频率高tabulator - 元老级 table 组件 高级功能平民化AG Grid - 媲美 Excel 的 Table 组件 能想到的复杂功能它都能做到...
)
Vue源码系列讲解——实例方法篇【三】(生命周期相关方法)
目录 0. 前言 1. vm.$mount 1.1 用法回顾 1.2 内部原理 2. vm.$forceUpdate 2.1 用法回顾 2.2 内部原理 3. vm.$nextTick 3.1 用法回顾 3.2 JS的运行机制 3.3 内部原理 能力检测 执行回调队列 4. vm.$destory 4.1 用法回顾 4.2 内部原理 0. 前言 与生命周期相关…...

百度SEO工具,自动更新网站的工具
在网站SEO的过程中,不断更新网站内容是提升排名和吸引流量的关键之一。而对于大多数网站管理员来说,频繁手动更新文章并进行SEO优化可能会是一项繁琐且耗时的任务。针对这一问题,百度自动更新文章SEO工具应运而生,它能够帮助网站管…...
供应链|NUS覃含章MS论文解读:数据驱动下联合定价和库存控制的近似方法 (二)
编者按 本次解读的文章发表于 Management Science,原文信息:Hanzhang Qin, David Simchi-Levi, Li Wang (2022) Data-Driven Approximation Schemes for Joint Pricing and Inventory Control Models. https://doi.org/10.1287/mnsc.2021.4212 文章在数…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...