【C++从0到王者】第四十六站:图的深度优先与广度优先
文章目录
- 一、图的遍历
- 二、广度优先遍历
- 1.思想
- 2.算法实现
- 3.六度好友
- 三、深度优先遍历
- 1.思想
- 2.代码实现
- 四、其他问题
一、图的遍历
对于图而言,我们的遍历一般是遍历顶点,而不是边,因为边的遍历是比较简单的,就是邻接矩阵或者邻接表里面的内容。而对于遍历顶点就稍微有点麻烦了。
给定一个图G和其中任意一个顶点v0,从v0出发,沿着图中各边访问图中的所有顶点,且每个顶点仅被遍历一次。"遍历"即对结点进行某种操作的意思。
树以前前是怎么遍历的,此处可以直接用来遍历图吗?为什么?
树以前的遍历有深度优先(先序、中序、后序)和广度优先遍历(层序遍历)两种。
图也是类似的。
二、广度优先遍历
1.思想
下面是广度优先遍历的一个比较形象的例子
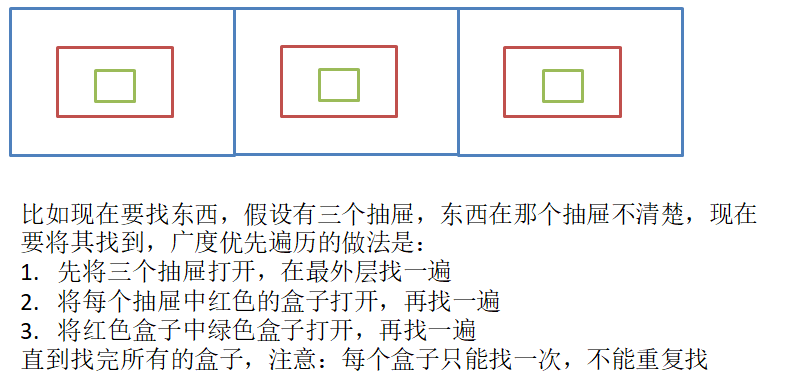
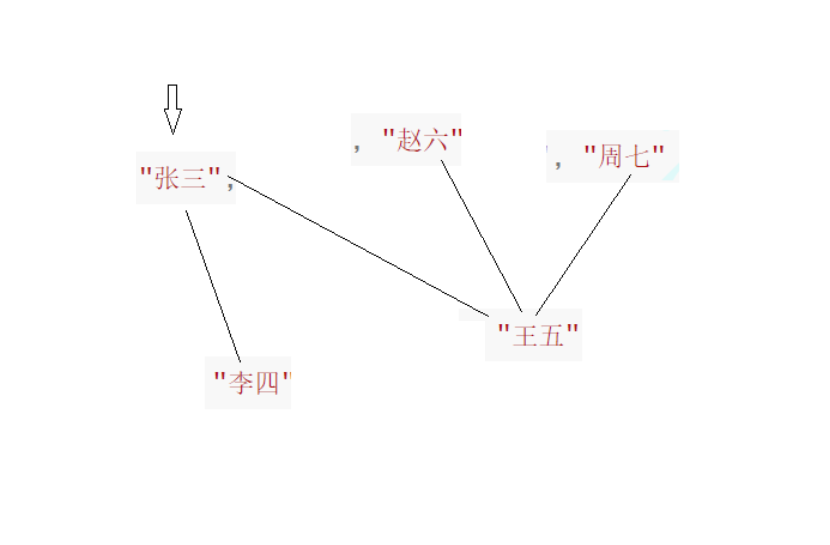
对于下面的图而言,也是类似的,先去找A,然后去遍历A的周围的三个结点,然后遍历这三个结点的周围结点,一层一层往外遍历,最终遍历完所有的结点,需要注意的是不要重复遍历了!
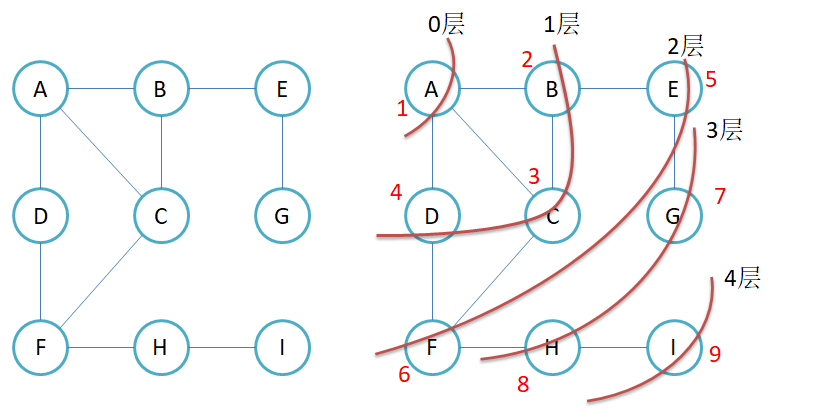
2.算法实现
我们这里用邻接矩阵来实现我们的代码。如下代码所示。
namespace matrix
{//V代表顶点, W是weight代表权值,MAX_W代表权值的最大值,Direction代表是有向图还是无向图,flase表示无向template<class V, class W, W Max_W = INT_MAX, bool Direction = false>class Graph{public://图的创建//1. IO输入 不方便测试//2. 图结构关系写到文件,读取文件//3. 手动添加边Graph(const V* a, size_t n){_vertexs.reserve(n);for (size_t i = 0; i < n; i++){_vertexs.push_back(a[i]);_indexMap[a[i]] = i;}_matrix.resize(n);for (size_t i = 0; i < _matrix.size(); i++){_matrix[i].resize(n, Max_W);}}size_t GetVertexIndex(const V& v){//return _indexMap[v];auto it = _indexMap.find(v);if (it != _indexMap.end()){return it->second;}else{//assert(false)throw invalid_argument("顶点不存在");return -1;}}void AddEdge(const V& src, const V& dst, const W& w){size_t srci = GetVertexIndex(src);size_t dsti = GetVertexIndex(dst);_matrix[srci][dsti] = w;if (Direction == false){_matrix[dsti][srci] = w;}}void Print(){for (size_t i = 0; i < _vertexs.size(); i++){cout << "[" << i << "]" << "->" << _vertexs[i] << endl;}cout << endl;cout << " ";for (int i = 0; i < _vertexs.size(); i++){//cout << _vertexs[i] << " ";printf("%-3d ", i);}cout << endl;for (size_t i = 0; i < _matrix.size(); i++){//cout << _vertexs[i] << " ";printf("%d ", i);for (size_t j = 0; j < _matrix[i].size(); j++){if (_matrix[i][j] == INT_MAX){cout << " * " << " ";}else{printf("%-3d ", _matrix[i][j]);//cout << _matrix[i][j] << " ";}}cout << endl;}}void BFS(const V& src){int srci = GetVertexIndex(src);queue<int> q; //广度遍历的队列vector<bool> visited(_vertexs.size(), false); //标记数组q.push(srci); //起点入队visited[srci] = true; //已经被遍历过了while (!q.empty()){int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << endl;//把front顶点的邻接顶点入队列for (size_t i = 0; i < _matrix[front].size(); i++){if (_matrix[front][i] != Max_W){if (visited[i] == false){q.push(i);visited[i] = true;}}}}} private:vector<V> _vertexs; //顶点集合map<V, int> _indexMap; //顶点对应的下标关系vector<vector<W>> _matrix; //临界矩阵};
在上面的代码当中,这个图的如下所示
在BFS的时候,我们使用一个队列和一个标记数组来解决。
我们先将第一个起点入队,并且进行标记已经被遍历了,然后像二叉树的层序遍历一样,一层一层去寻找它的周围结点。由于我们用的是邻接矩阵,那么我们就可以以出队列的这个结点为起点,遍历邻接矩阵的对应行,找到满足的进行入队列,然后依次进行标记。从而最终可以遍历整个图
最终结果为
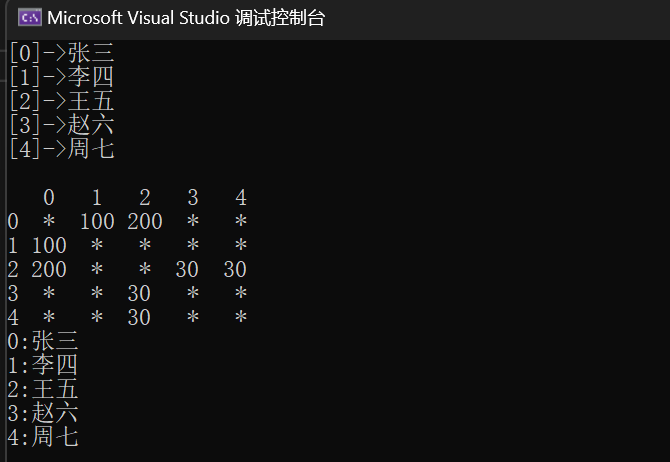
3.六度好友
如下面的题目就是一个简单的广度优先遍历
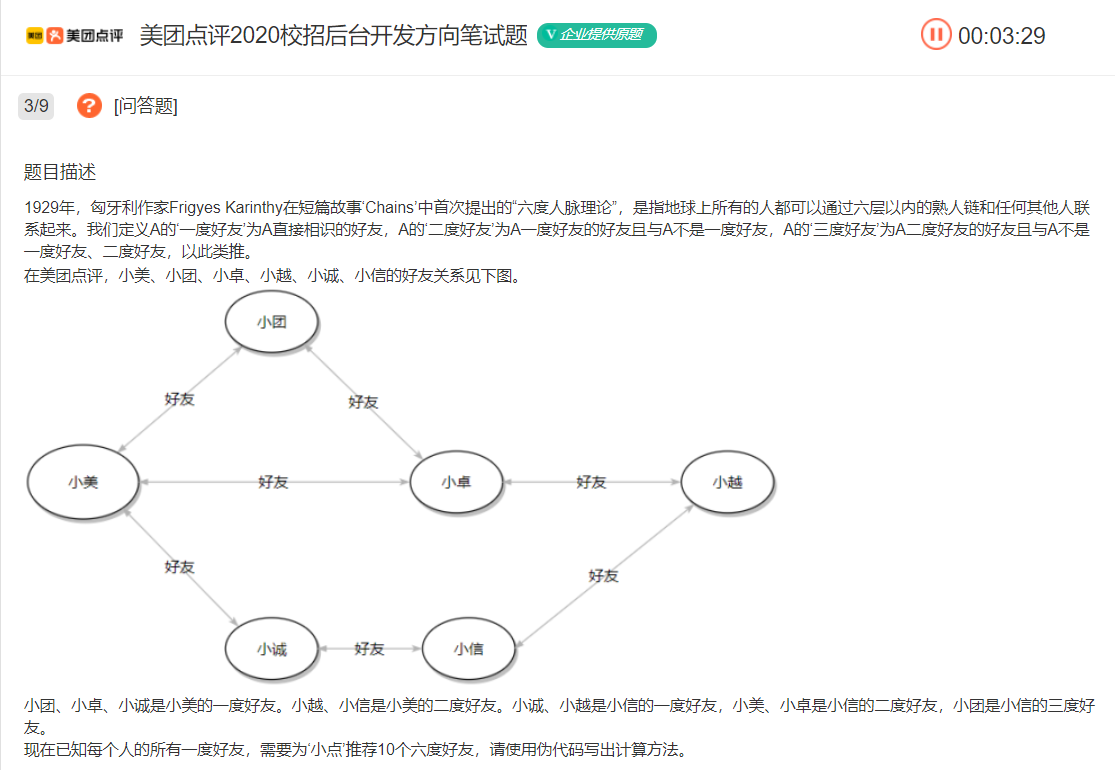
这道题与二叉树中求出第几层的元素是十分类似的。就是层序遍历,不过要打印出第六层的结果
void BFSLevel(const V& src)
{int srci = GetVertexIndex(src);queue<int> q; //广度遍历的队列vector<bool> visited(_vertexs.size(), false); //标记数组q.push(srci); //起点入队visited[srci] = true; //已经被遍历过了int levelSize = 1;while (!q.empty()){for (int i = 0; i < levelSize; i++){int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << " ";//把front顶点的邻接顶点入队列for (size_t i = 0; i < _matrix[front].size(); i++){if (_matrix[front][i] != Max_W){if (visited[i] == false){q.push(i);visited[i] = true;}}}}cout << endl;levelSize = q.size();}
}
void TestGraphBDFS()
{string a[] = { "张三", "李四", "王五", "赵六", "周七" };Graph<string, int> g1(a, sizeof(a) / sizeof(string));g1.AddEdge("张三", "李四", 100);g1.AddEdge("张三", "王五", 200);g1.AddEdge("王五", "赵六", 30);g1.AddEdge("王五", "周七", 30);g1.Print();g1.BFS("张三");cout << endl;g1.BFSLevel("张三");
}
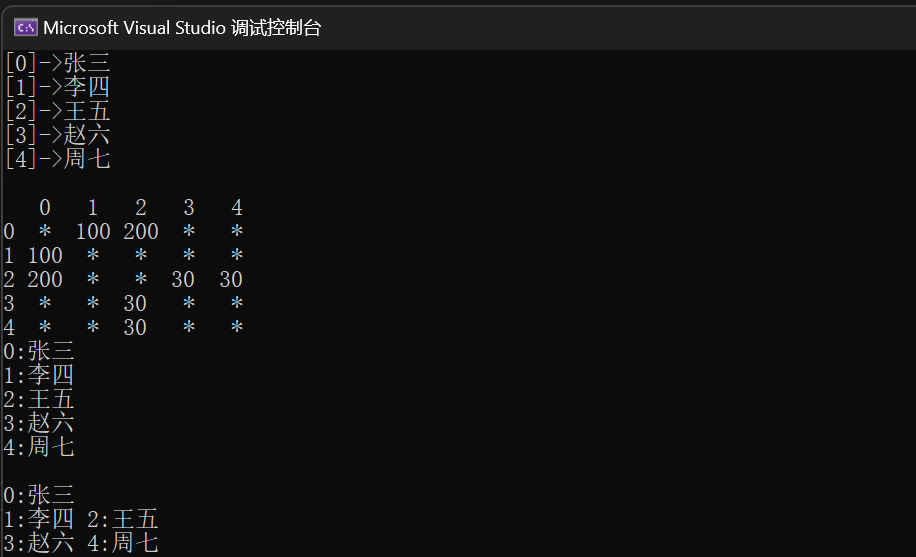
这里我们用一个循环来记录每层的个数,每打印够一层就换行。如上代码所示
运行结果为
三、深度优先遍历
1.思想

如上是深度优先的一个形象的案例,下面是深度优先在一个图中的实际场景
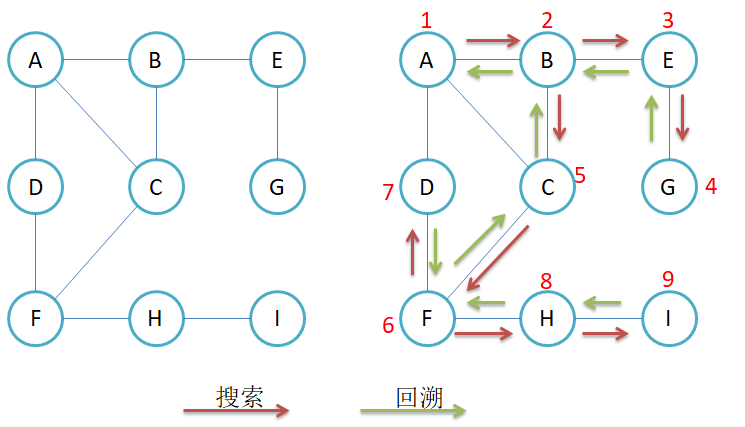
我们可以看到,他就像二叉树的先序遍历一样,一直走到最深层,然后退回去。这里需要注意的就是要进行标记已经遍历过的结点
2.代码实现
如下是深度优先的代码实现
namespace matrix
{//V代表顶点, W是weight代表权值,MAX_W代表权值的最大值,Direction代表是有向图还是无向图,flase表示无向template<class V, class W, W Max_W = INT_MAX, bool Direction = false>class Graph{public://图的创建//1. IO输入 不方便测试//2. 图结构关系写到文件,读取文件//3. 手动添加边Graph(const V* a, size_t n){_vertexs.reserve(n);for (size_t i = 0; i < n; i++){_vertexs.push_back(a[i]);_indexMap[a[i]] = i;}_matrix.resize(n);for (size_t i = 0; i < _matrix.size(); i++){_matrix[i].resize(n, Max_W);}}size_t GetVertexIndex(const V& v){//return _indexMap[v];auto it = _indexMap.find(v);if (it != _indexMap.end()){return it->second;}else{//assert(false)throw invalid_argument("顶点不存在");return -1;}}void AddEdge(const V& src, const V& dst, const W& w){size_t srci = GetVertexIndex(src);size_t dsti = GetVertexIndex(dst);_matrix[srci][dsti] = w;if (Direction == false){_matrix[dsti][srci] = w;}}void Print(){for (size_t i = 0; i < _vertexs.size(); i++){cout << "[" << i << "]" << "->" << _vertexs[i] << endl;}cout << endl;cout << " ";for (int i = 0; i < _vertexs.size(); i++){//cout << _vertexs[i] << " ";printf("%-3d ", i);}cout << endl;for (size_t i = 0; i < _matrix.size(); i++){//cout << _vertexs[i] << " ";printf("%d ", i);for (size_t j = 0; j < _matrix[i].size(); j++){if (_matrix[i][j] == INT_MAX){cout << " * " << " ";}else{printf("%-3d ", _matrix[i][j]);//cout << _matrix[i][j] << " ";}}cout << endl;}}void BFS(const V& src){int srci = GetVertexIndex(src);queue<int> q; //广度遍历的队列vector<bool> visited(_vertexs.size(), false); //标记数组q.push(srci); //起点入队visited[srci] = true; //已经被遍历过了while (!q.empty()){int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << endl;//把front顶点的邻接顶点入队列for (size_t i = 0; i < _matrix[front].size(); i++){if (_matrix[front][i] != Max_W){if (visited[i] == false){q.push(i);visited[i] = true;}}}}} void BFSLevel(const V& src){int srci = GetVertexIndex(src);queue<int> q; //广度遍历的队列vector<bool> visited(_vertexs.size(), false); //标记数组q.push(srci); //起点入队visited[srci] = true; //已经被遍历过了int levelSize = 1;while (!q.empty()){for (int i = 0; i < levelSize; i++){int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << " ";//把front顶点的邻接顶点入队列for (size_t i = 0; i < _matrix[front].size(); i++){if (_matrix[front][i] != Max_W){if (visited[i] == false){q.push(i);visited[i] = true;}}}}cout << endl;levelSize = q.size();}}void _DFS(size_t srci, vector<bool>& visited){cout << srci << ":" << _vertexs[srci] << endl;visited[srci] = true;for (int i = 0; i < _matrix[srci].size(); i++){if (_matrix[srci][i] != Max_W && visited[i] == false){_DFS(i, visited);}}}void DFS(const V& src){int srci = GetVertexIndex(src);vector<bool> visited(_vertexs.size(), false);_DFS(srci, visited);}private:vector<V> _vertexs; //顶点集合map<V, int> _indexMap; //顶点对应的下标关系vector<vector<W>> _matrix; //临界矩阵};void TestGraph(){Graph<char, int, INT_MAX, true> g("0123", 4);g.AddEdge('0', '1', 1);g.AddEdge('0', '3', 4);g.AddEdge('1', '3', 2);g.AddEdge('1', '2', 9);g.AddEdge('2', '3', 8);g.AddEdge('2', '1', 5);g.AddEdge('2', '0', 3);g.AddEdge('3', '2', 6);g.Print();}void TestGraphBDFS(){string a[] = { "张三", "李四", "王五", "赵六", "周七" };Graph<string, int> g1(a, sizeof(a) / sizeof(string));g1.AddEdge("张三", "李四", 100);g1.AddEdge("张三", "王五", 200);g1.AddEdge("王五", "赵六", 30);g1.AddEdge("王五", "周七", 30);g1.Print();g1.BFS("张三");cout << endl;g1.BFSLevel("张三");cout << endl;g1.DFS("张三");}}
像先序遍历一样,这里也是需要一个子函数比较好的,因为我们需要使用递归,让子函数去进行递归是最好的
运行结果如下所示
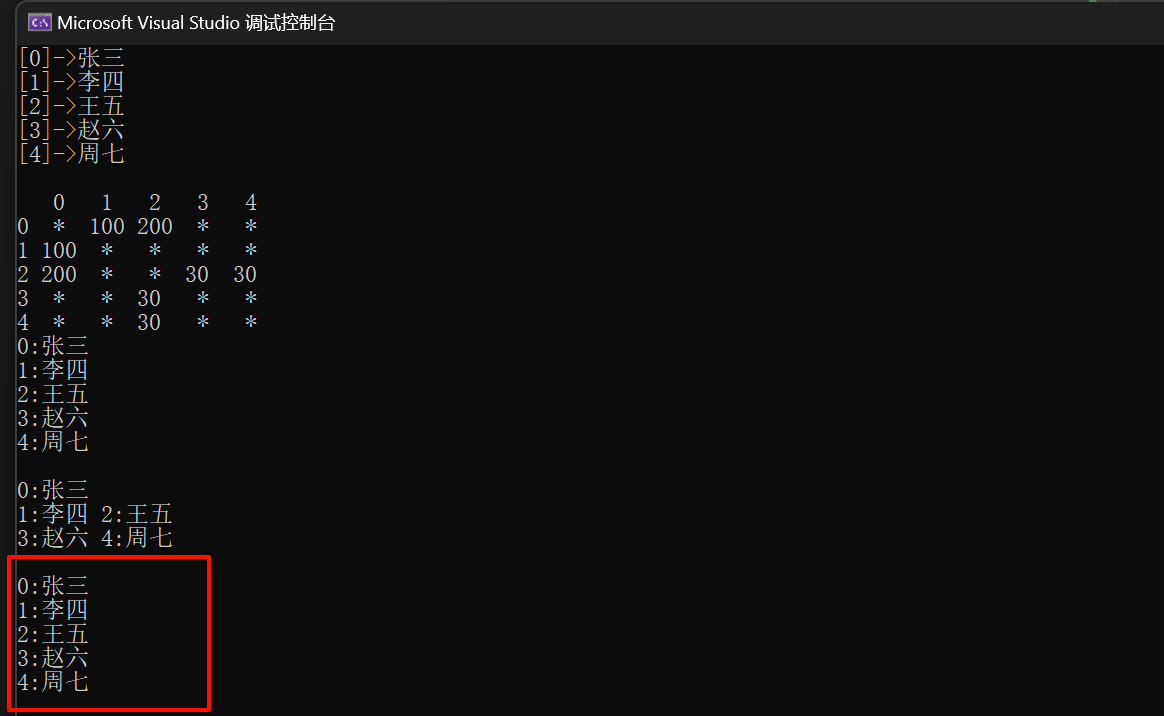
四、其他问题
关于深度优先和广度优先,上面的清空自然是很理想的情况。并且由于起点不同,深度优先和广度优先的结果是不同的。但是有时候,也会出现下面的问题。
比如图不连通的问题。也就是图存在孤立的结点。那么这样的话,以某个点为起点就没有遍历完成
这里我们可以有个解决方案是从visited数组中寻找没有遍历的结点,在进行一次深度优先或者广度优先。也就是要在原来的代码上在套一层。
相关文章:

【C++从0到王者】第四十六站:图的深度优先与广度优先
文章目录 一、图的遍历二、广度优先遍历1.思想2.算法实现3.六度好友 三、深度优先遍历1.思想2.代码实现 四、其他问题 一、图的遍历 对于图而言,我们的遍历一般是遍历顶点,而不是边,因为边的遍历是比较简单的,就是邻接矩阵或者邻接…...

Docker技术概论(2):Docker环境的搭建
Docker技术概论(2) Docker环境的搭建 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this article:https://blo…...
电脑休眠之后唤不醒
现象:午休时间电脑休眠了,醒来之后发现在密码输入界面,但鼠标键盘没反应。按重启键或电源机重新开机,结果开不了机。 原因:1、内存条脏了,导致内存条读取失败 2、休眠的时候硬盘休眠了,导致按…...

Python列表中添加删除元素不走弯路
1.append() 向列表中添加单个元素,一般用于尾部追加 list1 ["香妃", "乾隆", "贾南风", "赵飞燕", "汉武帝"]list1.append("周瑜") print(list1) # [香妃, 乾隆, 贾南风, 赵飞燕, 汉武帝, 周瑜]…...
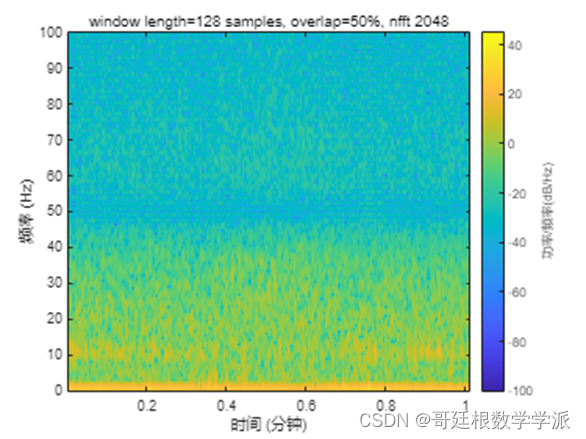
MATLAB环境下脑电信号EEG的谱分析
脑电信号一直伴随着人类的生命,脑电波是脑神经细胞发生新陈代谢、离子交换时细胞群兴奋突触电位总和,脑电信号的节律性则和丘脑相关,含有丰富的大脑活动信息。通常我们所接触的脑电图都是头皮脑电图,在有些特殊场合还需要皮下部位…...
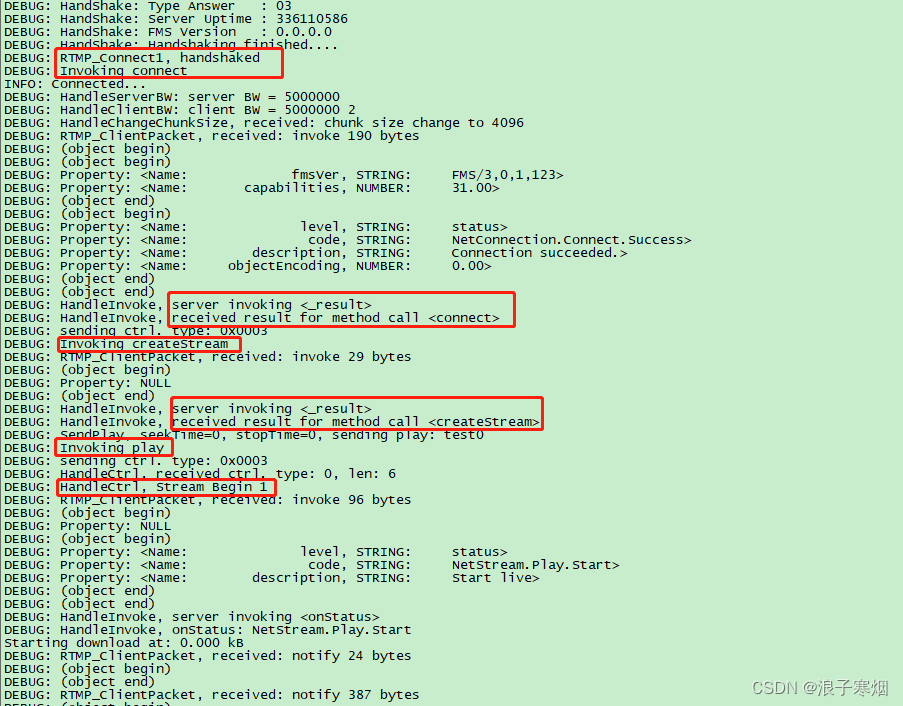
librtmp源码分析
阅读了librtmp的源码,简单记录下。 首先补充下AMF格式基本知识 1 AMF格式 AMF是Action Message Format(动作消息格式)的简写,它是一种二进制的数据格式。它的设计是为了把actionscript里面的数据(包括Object, Array, Boolean, Number等)序列化成二进制…...

CCDP.00.问老师问题前你首先需要做的事情
一、一定要按老师要求做好快照!!!!! 1、在关键节点处,比如做完Part1后,关机状态下做快照。 2、在做没把握的操作前先做快照(这个可以在开机状态下做快照,但推荐关机状态…...

「算法」常见位运算总结
位运算符 异或 按位异或可以实现无进位相加,所谓无进位相加,就是在不考虑进位的情况下将两个数相加(后面有道题需要用到这种操作) 异或的运算律 ①a ^ 0 a ②a ^ a 0 ③a ^ b ^ c a ^ ( b ^ c ) 有符号右移>> 将一个…...
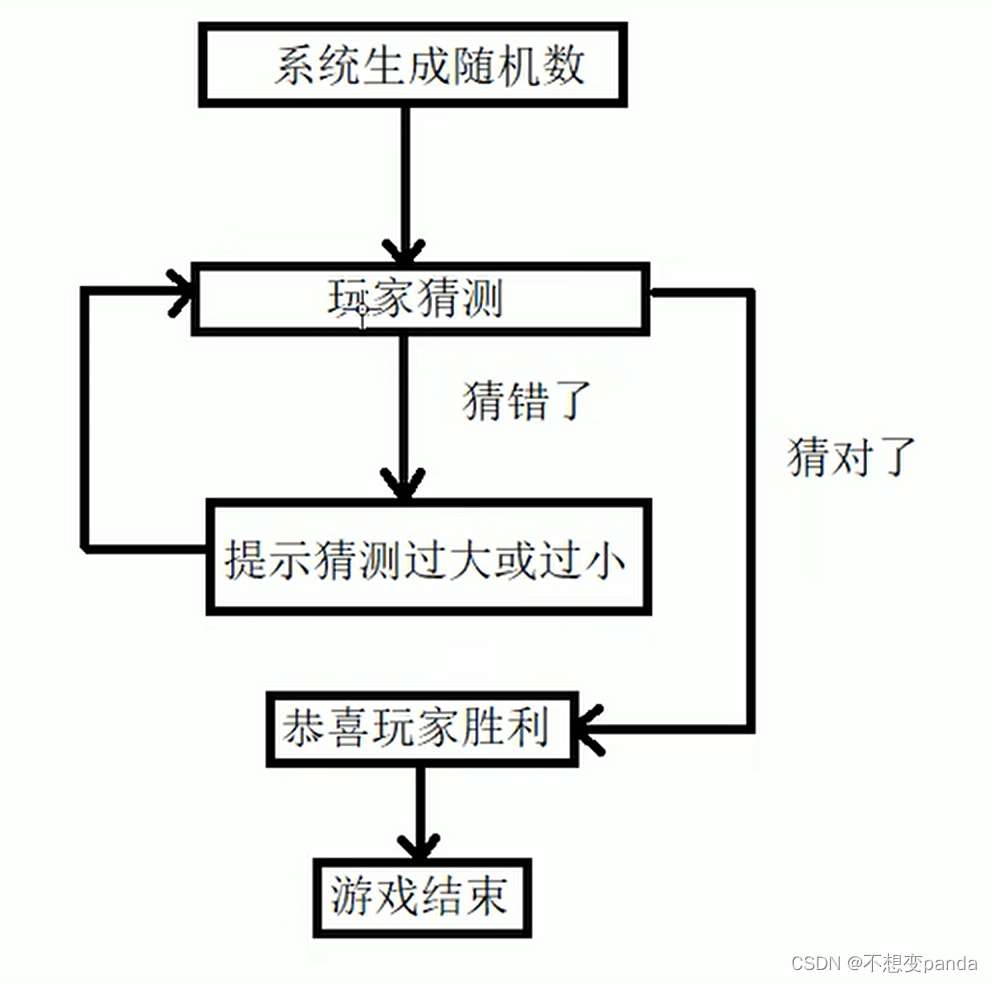
【C++初识】语句
文章目录 1.注释 变量 常量 关键字 标识符命名规则 数据类型 sizeof关键字 数据的输入 运算符2.程序流程结构2.1选择结构2.2循环结构2.21while{循环条件}{循环语句};//满足循环条件,执行循环语句2.22do{循环语句}while{循环条件};//do....whi…...

Python线性代数傅里叶分析和动态系统模拟分析之一
要点 Python向量数值计算、可视化,线性独立性和子空间。了解欧几里德距离、余弦相似度和皮尔逊相关性应用案例:Python数值计算文档相似度时间序列和特征检测示例:Python信号处理边缘检测器, K均值示例:随机簇质心分布Python傅里叶…...
)
mysql插入GEOMETRY相关字段类型(point,linestring等)
一、问题 向mysql中插入point,linestring等相关空间坐标字段,出现报错: 1416 - Cannot get geometry object from data you send to the GEOMETRY field要插入的数据:...

vue3学习 【5】watch的使用
什么是watch 当我们需要根据一个数据的变化来进行一些操作的时候我们需要使用侦听器,它能够在响应式数据发生变化的时候触发提供的回调函数 基础侦听 watch 可以侦听不同的数据源。例如: ref计算属性响应式对象getter函数多个数据源组层的数据 cons…...
PyTorch深度学习快速入门
PyTorch深度学习快速入门 1.PyTorch环境配置及安装2.python编辑器的选择、安装、配置(pycharm、JupyTer安装)3.为什么torch.cuda.is_available()返回false4.python学习中两大法宝函数(也可用在pytorch)5.pycharm和jupyter…...
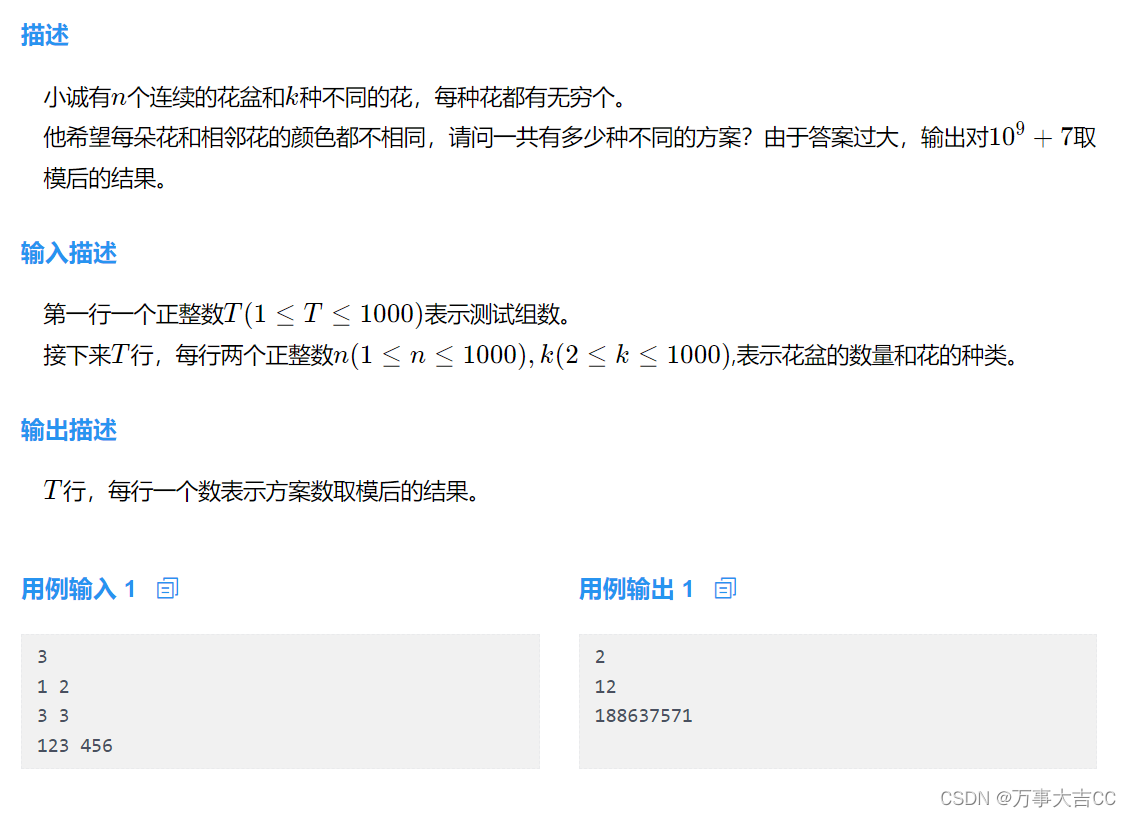
种花
分情况: 第一盆k种选择,之后全部k-1种选择 每次相乘结果对1e97取模 #include <iostream> #include <vector> #include <algorithm> using namespace std; #define endl \n const int N 1e9 7;int main() {ios::sync_with_stdio(f…...
)
Android Shadow插件化框架分析与集成(二)
本文索引 前言插件打包后如何交给宿主使用?宿主加载插件代码分析全局初始化操作加载插件activity测试过程中遇到的问题报错 1 :报错2:报错3 :二次开发支持多插件、多进程功能mPpsController 的构造方式mPluginLoader的构造方式多插件如何改造前言...

Go 与 Rust:导航编程语言景观
在当今构建软件时,开发者在编程语言上有着丰富的选择。两种脱颖而出的语言是 Go 和 Rust - 都很强大但却截然不同。本文将从各种因素比较这两种语言,以帮助您确定哪种更适合您的需求。 我们将权衡它们在并发、安全性、速度、互操作性等方面的方法。我们将…...

包管理工具之npm也慌了?
起因 因为npm的种种问题,我很早就换成了pnpm和yarn(但是其实npm也在使用),已经很久没有关注npm的功能更新了。最近无意间进入Node18版本的安装目录,发现其除了常规的node,npm等默认安装了一个新的包corepack,这个就是今天我要分享的东西了。 注: 我因为18版本的node上…...
mobile app 安全扫描工具MobSF了解下
可以干啥: static 静态分析 dynamic 动态分析 可以用来渗透了 如何docker安装 docker image 下载地址https://hub.docker.com/r/opensecurity/mobile-security-framework-mobsf/ setup 两行即可 1 docker pull opensecurity/mobile-security-framework-mobsf…...

Gophish+EwoMail 自建钓鱼服务器
GophishEwoMail 自建钓鱼服务器 文章目录 GophishEwoMail 自建钓鱼服务器1.前提准备2.搭建EwoMail邮件服务器1)Centos7 防火墙操作2)设置主机名3)host配置4)安装EwoMail5)获取DKIM6)端口服务介绍7ÿ…...

Dockerfile(5) - CMD 指令详解
CMD 指定容器默认执行的命令 # exec 形式,推荐 CMD ["executable","param1","param2"] CMD ["可执行命令", "参数1", "参数2"...]# 作为ENTRYPOINT的默认参数 CMD ["param1","param…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...