LeetCode_22_中等_括号生成
文章目录
- 1. 题目
- 2. 思路及代码实现(Python)
- 2.1 暴力法
- 2.2 回溯法
1. 题目
数字 n n n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
输入: n = 3 n = 3 n=3
输出: [ " ( ( ( ) ) ) " , " ( ( ) ( ) ) " , " ( ( ) ) ( ) " , " ( ) ( ( ) ) " , " ( ) ( ) ( ) " ] ["((()))","(()())","(())()","()(())","()()()"] ["((()))","(()())","(())()","()(())","()()()"]
示例 2:
输入: n = 1 n = 1 n=1
输出: [ " ( ) " ] ["()"] ["()"]
提示:
- 1 ≤ n ≤ 8 1 \leq n \leq 8 1≤n≤8
2. 思路及代码实现(Python)
2.1 暴力法
该思路先生成所有的 2 2 n 2^{2n} 22n 个 “(” 和 “)” 字符串构成的序列,然后检查生成的序列是否有效,一共有 n n n 对括号,共 2 n 2n 2n 个字符,每个位置存在两种不同的选择,因此总共有 2 2 n 2^{2n} 22n 种序列。
为了生成所有序列,可以使用递归。长度为 n n n 的序列就是在长度为 n − 1 n−1 n−1 的序列后加一个 “(” 或 “)”。为了检查序列是否有效,我们遍历这个序列,并使用一个变量 b a l bal bal 表示左括号的数量减去右括号的数量。如果在遍历过程中 b a l bal bal 的值小于零,或者结束时 b a l bal bal 的值不为零,那么该序列就是无效的,否则它是有效的。前者说明,遍历一段字符串时出现 “)” 大于 “(” 的数量,显然说明该子串不能成对;而后者说明整个字符串的左右括号数并不相等。
该算法的时间复杂度为: O ( 2 2 n n ) O(2^{2n}n) O(22nn),对于 2 2 n 2^{2n} 22n 个序列中的每一个,对其进行有效性的验证的复杂度为 O ( n ) O(n) O(n)。而空间复杂度除了存储答案组之外,还需要存储探索答案的栈深,复杂度为 O ( n ) O(n) O(n)。
class Solution:def generateParenthesis(self, n: int):def generate(A):if len(A) == 2*n:if valid(A):ans.append("".join(A))else:A.append('(')generate(A)A.pop()A.append(')')generate(A)A.pop()def valid(A):bal = 0for c in A:if c == '(': bal += 1else: bal -= 1if bal < 0: return Falsereturn bal == 0ans = []generate([])return ans
执行用时:71 ms
消耗内存:16.54 MB
2.2 回溯法
上述方法是遍历生成所有的可能的序列,然后再进行判断,这里我们发现有可以改进的地方,就是在生成序列时,提前跟踪序列的左右括号的数据,来决定扩展序列时所选择的括号。例如,已有子序列的左括号数量不大于 n n n,则可以放置左括号,如果右括号数量小于左括号数量,可以放置一个右括号。
该算法的复杂度分析依赖于该有效序列可以回溯出 的元素个数。这证明是第 n n n 个卡特兰数 1 n + 1 ( 2 n n ) \dfrac{1}{n+1}\dbinom{2n}{n} n+11(n2n) ,这是由 4 n n n \dfrac{4^n}{n\sqrt{n}} nn4n 渐近界定的。因此时间复杂度为 O ( 4 n n ) O(\dfrac{4^n}{\sqrt{n}}) O(n4n)。空间复杂度为保存答案和保存栈深的消耗,为 O ( n ) O(n) O(n)。
class Solution:def generateParenthesis(self, n: int):ans = []def backtrack(S, left, right):if len(S) == 2 * n:ans.append(''.join(S))returnif left < n:S.append('(')backtrack(S, left+1, right)S.pop()if right < left:S.append(')')backtrack(S, left, right+1)S.pop()backtrack([], 0, 0)return ans
执行用时:42 ms
消耗内存:16.55 MB
题解来源:力扣官方题解
相关文章:

LeetCode_22_中等_括号生成
文章目录 1. 题目2. 思路及代码实现(Python)2.1 暴力法2.2 回溯法 1. 题目 数字 n n n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。 示例 1: 输入: n 3 n 3 …...
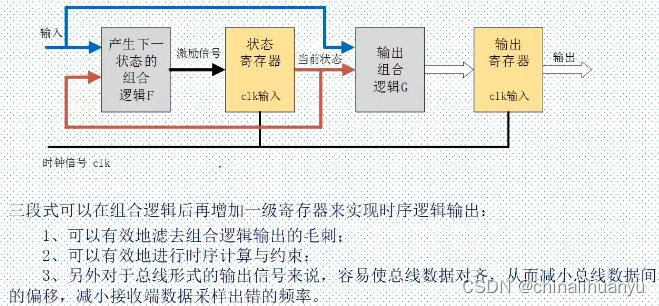
Verilog(未完待续)
Verilog教程 这个教程写的很好,可以多看看。本篇还没整理完。 一、Verilog简介 什么是FPGA?一种可通过编程来修改其逻辑功能的数字集成电路(芯片) 与单片机的区别?对单片机编程并不改变其地电路的内部结构࿰…...

【Linux实践室】Linux初体验
🌈个人主页:聆风吟 🔥系列专栏:Linux实践室、网络奇遇记 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 一. ⛳️任务描述二. ⛳️相关知识2.1 🔔Linux 目录结构介绍2.2 🔔Linux …...

Flutter中高级JSON处理:使用json_serializable进行深入定制
Flutter中高级JSON处理 使用json_serializable库进行深入定制 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at: https://jclee95.blog.csdn.netEmail: 291148484163.com. Shenzhen ChinaAddress of this article:https://blog.csdn.net/qq_28550263/article/details/1363…...

华为OD技术面试案例4-2024年
个人情况:985本,目标院校非计算机专业,情况比较特殊,23年11月研究生退学,电子信息类专业。 初识od:10月底打算退学的时候在智联、BOSS上疯狂投硬件方面的岗位。投了大概一两天后有德科和HW的HR打电话给我介…...
 重试机制与监听器的使用)
【TestNG】(4) 重试机制与监听器的使用
在UI自动化测试用例执行过程中,经常会有很多不确定的因素导致用例执行失败,比如网络原因、环境问题等,所以我们有必要引入重试机制(失败重跑),来提高测试用例成功率。 在不写代码的情况没有提供可配置方式…...

“智农”-高标准农田
高标准农田是指通过土地整治、土壤改良、水利设施、农电配套、机械化作业等措施,提升农田质量和生产能力,达到田块平整、集中连片、设施完善、节水高效、宜机作业、土壤肥沃、生态友好、抗灾能力强、与现代农业生产和经营方式相适应的旱涝保收、稳产高产…...
方法在网页中快速查找元素)
利用 lxml 库的XPath()方法在网页中快速查找元素
XPath() 函数是 lxml 库中 Element 对象的方法。在使用 lxml 库解析 HTML 或 XML 文档时,您可以通过创建 Element 对象来表示文档的元素,然后使用 Element 对象的 XPath() 方法来执行 XPath 表达式并选择相应的元素。 具体而言,XPath() 方法是…...
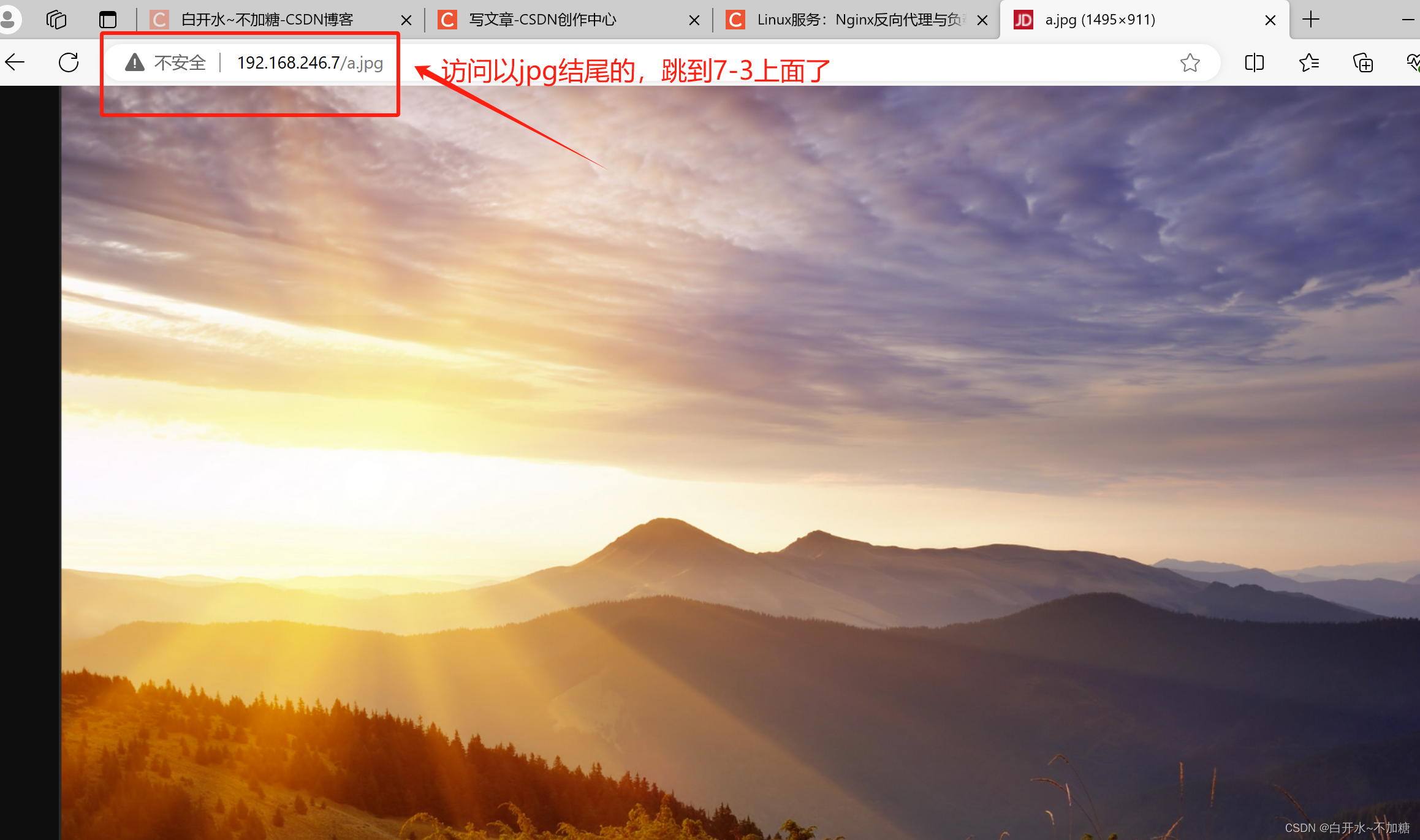
nginx---------------重写功能 防盗链 反向代理 (五)
一、重写功能 rewrite Nginx服务器利用 ngx_http_rewrite_module 模块解析和处理rewrite请求,此功能依靠 PCRE(perl compatible regular expression),因此编译之前要安装PCRE库,rewrite是nginx服务器的重要功能之一,重写功能(…...

unity shaderGraph实例-物体线框显示
文章目录 本项目基于URP实现一,读取UV网格,由自定义shader实现效果优缺点效果展示模型准备整体结构各区域内容区域1区域2区域3区域4shader属性颜色属性材质属性后处理 实现二,直接使用纹理,使用默认shader实现优缺点贴图准备材质准…...
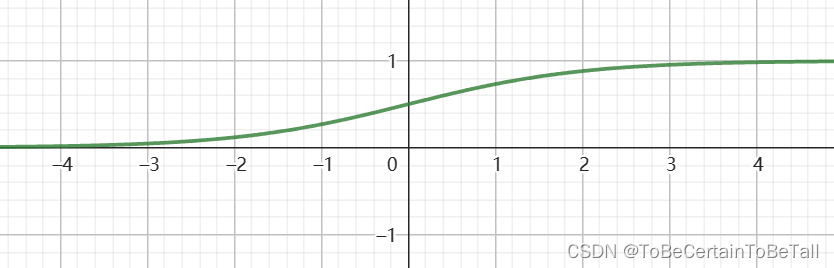
分类问题经典算法 | 二分类问题 | Logistic回归:公式推导
目录 一. Logistic回归的思想1. 分类任务思想2. Logistic回归思想 二. Logistic回归算法:线性可分推导 一. Logistic回归的思想 1. 分类任务思想 分类问题通常可以分为二分类,多分类任务;而对于不同的分类任务,训练的主要目标是…...
redis实现分布式全局唯一id
目录 一、前言二、如何通过Redis设计一个分布式全局唯一ID生成工具2.1 使用 Redis 计数器实现2.2 使用 Redis Hash结构实现 三、通过代码实现分布式全局唯一ID工具3.1 导入依赖配置3.2 配置yml文件3.3 序列化配置3.4 编写获取工具3.5 测试获取工具 四、运行结果 一、前言 在很…...

Sora引发安全新挑战
文章目录 前言一、如何看待Sora二、Sora加剧“深度伪造”忧虑三、Sora无法区分对错四、滥用导致的安全危机五、Sora面临的安全挑战总结前言 今年2月,美国人工智能巨头企业OpenAI再推行业爆款Sora,将之前ChatGPT以图文为主的生成式内容全面扩大到视频领域,引发了全球热议,这…...

Android 14.0 Launcher3定制化之桌面分页横线改成圆点显示功能实现
1.前言 在14.0的系统rom产品定制化开发中,在进行launcher3的定制化中,在双层改为单层的开发中,在原生的分页 是横线,而为了美观就采用了系统原来的另外一种分页方式,就是圆点比较美观,接下来就来分析下相关…...
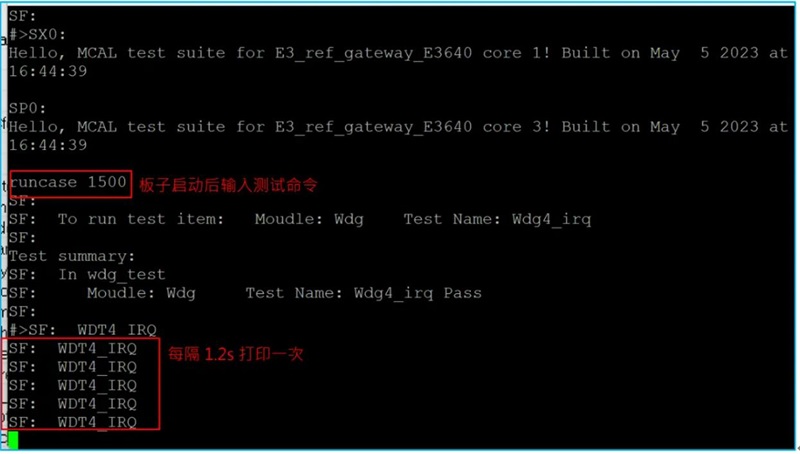
SemiDrive E3 MCAL 开发系列(3)– Wdg 模块的使用
一、 概述 本文将会介绍 SemiDrive E3 MCAL Wdg 模块的基本配置,并且会结合实际操作的介绍,帮助新手快速了解并掌握这个模块的使用,文中的 MCAL 是基于 PTG3.0 的版本,开发板是官方的 E3640 网关板。 二、 Wdg 模块的主要配置 …...

AI推荐算法的演进之路
推荐算法 基于大数据和AI技术,提供全流程一站式推荐平台,协助企业构建个性化推荐应用,提升企业应用的点击率留存率和永久体验。目前,主要的推荐方法包括:基于内容推荐、协同过滤推荐、基于关联规则推荐、基于效用推荐…...
Tomcat安装,配置文件、组件
一、Tomcat的基本功能 1.1.Tomcat是什么? Tomcat服务器是一个免费的开放源代码的Web应用服务器,属于轻量级应用服务器,在中小型系统和并发访问用户不是很多的场合下被普遍使用,是开发和调试JSP程序的首选。一般来说,T…...

精读《React Hooks 最佳实践》
简介 React 16.8 于 2019.2 正式发布,这是一个能提升代码质量和开发效率的特性,笔者就抛砖引玉先列出一些实践点,希望得到大家进一步讨论。 然而需要理解的是,没有一个完美的最佳实践规范,对一个高效团队来说&#x…...

varFormatter 数据格式化库 以性能优先的 快速的 内存对象格式转换
varFormatter 数据格式化 技术 开源技术栏 对象/变量格式化工具库,其支持将一个对象进行按照 JSON XML HTML 等格式进行转换,并获取到结果字符串! 目录 文章目录 varFormatter 数据格式化 技术目录介绍获取方式 使用实例格式化组件的基本使…...
基于PHP的在线英语学习平台
有需要请加文章底部Q哦 可远程调试 基于PHP的在线英语学习平台 一 介绍 此在线英语学习平台基于原生PHP开发,数据库mysql。系统角色分为学生,教师和管理员。(附带参考设计文档) 技术栈:phpmysqlphpstudyvscode 二 功能 学生 1 注册/登录/…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...
