【LeetCode每日一题】【BFS模版与例题】863.二叉树中所有距离为 K 的结点
BFS的基本概念
BFS 是广度优先搜索(Breadth-First Search)的缩写,是一种图遍历算法。它从给定的起始节点开始,逐层遍历图中的节点,直到遍历到目标节点或者遍历完所有可达节点。
BFS 算法的核心思想是先访问当前节点的所有邻居节点,然后再访问邻居节点的邻居节点,依此类推,直到遍历完整个图。
BFS 模版
BFS 使用队列(Queue)数据结构来辅助实现,它按照先进先出(FIFO)的顺序管理待访问的节点。用**集合(Set)**来辅助节点是否已经被访问,算法的基本流程如下:
- 将起始节点放入队列中,并标记为已访问。
- 从队列中取出一个节点,访问该节点,判断该节点是否符合条件。
- 将该节点的所有未访问过的邻居节点加入队列,并标记为已访问。
- 重复步骤 2 和步骤 3,直到队列为空。
模版1:不必记录深度
function BFS(start, target) {const queue = []; // 核心数据结构const visited = new Set(); // 避免走回头路// 将起始节点放入队列中,并标记为已访问。queue.push(start); visited.add(start);while (queue.length > 0) {const sz = queue.length;const cur = queue.shift();/* 划重点:这里判断是否到达终点 */if (cur === target)return step;/* 将 cur 的所有未访问过的邻居节点加入队列,并标记为已访问。 */for (const x of cur.adj()) {if (!visited.has(x)) {queue.push(x);visited.add(x);}}}
}
模版2:需要记录深度的
function BFS(start, target) {const queue = []; // 核心数据结构const visited = new Set(); // 避免走回头路// 将起始节点放入队列中,并标记为已访问。queue.push(start); visited.add(start);let step = 0; // 记录扩散的步数while (queue.length > 0) {const sz = queue.length;/* 将当前队列中的所有节点向四周扩散 */for (let i = 0; i < sz; i++) {const cur = queue.shift();/* 划重点:这里判断是否到达终点 */if (cur === target)return step;/* 将 cur 的所有未访问过的邻居节点加入队列,并标记为已访问。 */for (const x of cur.adj()) {if (!visited.has(x)) {queue.push(x);visited.add(x);}}}/* 划重点:更新步数在这里 */step++;}
}
BFS 算法通常用于以下场景:
- 寻找两个节点之间的最短路径。
- 在树或图中寻找特定深度或层级的节点。
- 检查图是否是连通的。
- 拓扑排序。
- 解决迷宫问题等。
例题
111 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
var minDepth = function(root) {if(root === null){return 0;}// 记录深度let step = 0;// BFS关键数据结构let queue = [];let visited = new Set();queue.push(root);visited.add(root);while(queue.length > 0){let size = queue.length;for(let i = 0;i<size;i++){/* 划重点:这里判断是否到达终点 */let node = queue.shift();if(node.left === null && node.right === null){return step+1;}/* 将 cur 的所有未访问过的邻居节点加入队列,并标记为已访问。 */if(node.left !== null && !visited.has(node.left)){queue.push(node.left);visited.add(node.left);}if(node.right !== null && !visited.has(node.right)){queue.push(node.right);visited.add(node.right);}}step++;}return step;
};
863.二叉树中所有距离为 K 的结点
给定一个二叉树(具有根结点 root), 一个目标结点 target ,和一个整数值 k 。
返回到目标结点 target 距离为 k 的所有结点的值的列表。 答案可以以 任何顺序 返回。
思路:
需要我们在树中寻找特定深度或层级的节点,但是又不是从根节点开始,因此需要我们将树 转化成 图。
可以通过哈希表和DFS将树转化成图
var distanceK = function(root, target, k) {// 起点是target,先通过哈希表+DFS将树转化成图const parents = getParents(root);// 结果数组let ans = []// BFS关键数据结构let queue = []const visited = new Set()queue.push(target);visited.add(target.val);// 记录深度let step = 0;while(queue.length){// 遍历每一层的节点const len = queue.length;for(let i = 0;i<len;i++){// 判断当前节点是否符合条件。const node = queue.shift();if(step === k){ans.push(node.val);}// 将相邻的节点都放入到if(node.left && !visited.has(node.left.val)){queue.push(node.left);visited.add(node.left.val);}if(node.right && !visited.has(node.right.val)){queue.push(node.right);visited.add(node.right.val);}if(parents.has(node.val) && !visited.has(parents.get(node.val).val)){queue.push(parents.get(node.val));visited.add(parents.get(node.val).val);}}// 遍历完一层后深度+1step++;}return ans;};function getParents(root) {const parents = new Map();const findParents = (root) => {if (root.left) {parents.set(root.left.val, root);findParents(root.left);}if (root.right) {parents.set(root.right.val, root);findParents(root.right);}};findParents(root);return parents;
}相关文章:

【LeetCode每日一题】【BFS模版与例题】863.二叉树中所有距离为 K 的结点
BFS的基本概念 BFS 是广度优先搜索(Breadth-First Search)的缩写,是一种图遍历算法。它从给定的起始节点开始,逐层遍历图中的节点,直到遍历到目标节点或者遍历完所有可达节点。 BFS 算法的核心思想是先访问当前节点的…...

设计模式-结构模式-装饰模式
装饰模式(Decorator Pattern):动态地给一个对象增加一些额外的职责,就增加对象功能来说,装饰模式比生成子类实现更为灵活。装饰模式是一种对象结构型模式。 //首先,定义一个组件接口: public in…...
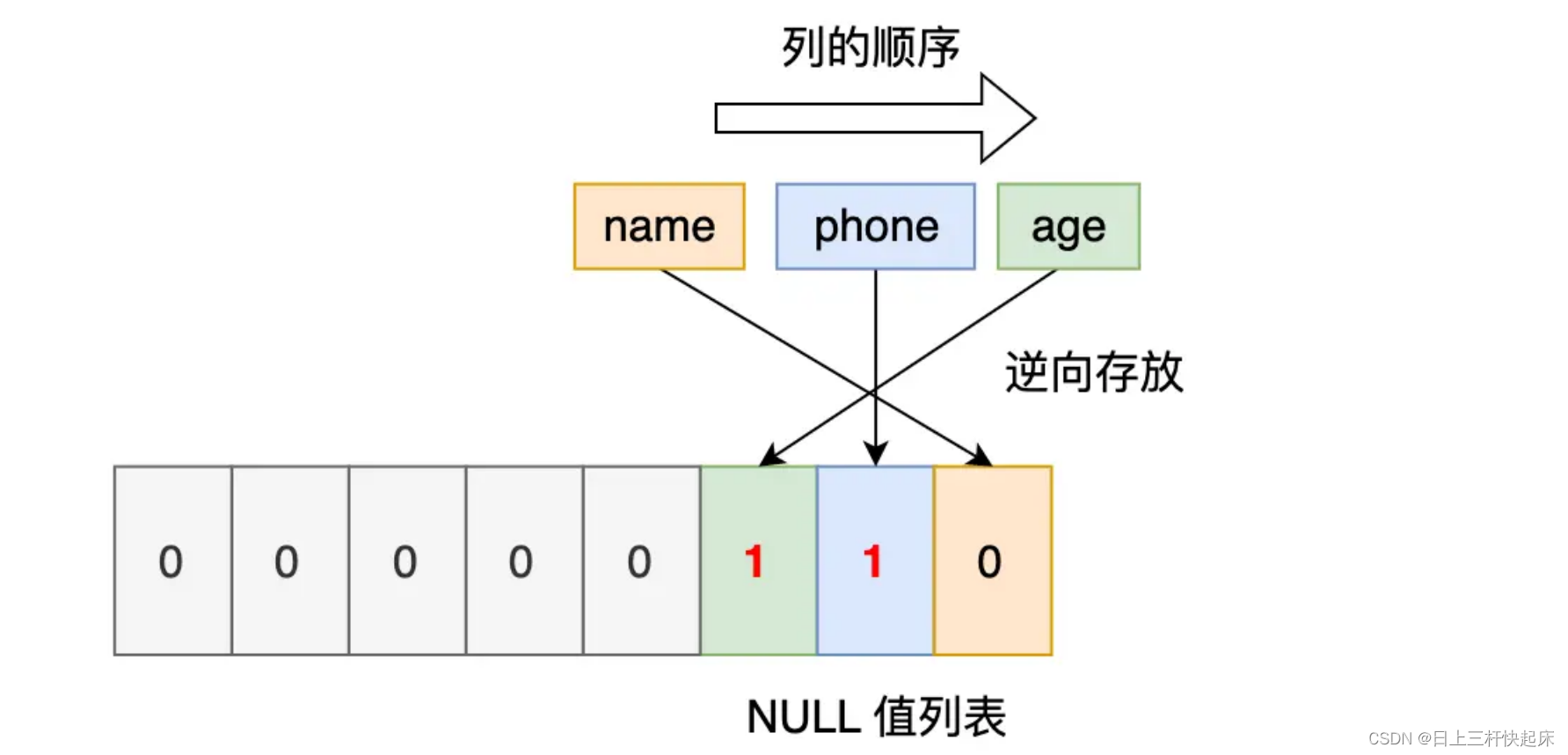
MySQL:一行记录如何
1、表空间文件结构 表空间由段「segment」、区「extent」、页「page」、行「row」组成,InnoDB存储引擎的逻辑存储结构大致如下图: 行 数据库表中的记录都是按「行」进行存放的,每行记录根据不同的行格式,有不同的存储结构。 页…...

‘grafana.ini‘ is read only ‘defaults.ini‘ is read only
docker安装grafana 关闭匿名登录情况下的免密登录遇到问题 grafana.ini is read only defaults.ini is read only 参考回答(Grafana.ini giving me the creeps - #2 by bartweemaels - Configuration - Grafana Labs Community Forums) 正确启动脚本 …...
博途PLC 面向对象系列之“输送带控制功能块“(SCL代码)
这篇是面向对象系列之"输送带功能块"的封装,面向对象是系列文章,相关链接如下: 1、面向对象系列之找"对象" https://rxxw-control.blog.csdn.net/article/details/136150027https://rxxw-control.blog.csdn.net/article/details/1361500272、面向对象…...
2024-02学习笔记
1.当我们向Set集合中添加一个已经存在的元素时 当我们向Set集合中添加一个已经存在的元素时,Set集合会如何处理呢?实际上,Set集合不会将重复的元素添加到集合中。当我们向Set集合中添加一个元素时,Set集合会首先判断该元素是否已…...

最新消息:英特尔宣布成立全新独立运营的FPGA公司——Altera
今天,英特尔宣布成立全新独立运营的FPGA公司——Altera(2015年6月Intel以 167 亿美元的价格,收购FPGA厂商Altera)。首席执行官Sandra Rivera和首席运营官Shannon Poulin分享展示其在超过550亿美元的市场中保持领先性的战略规划&am…...
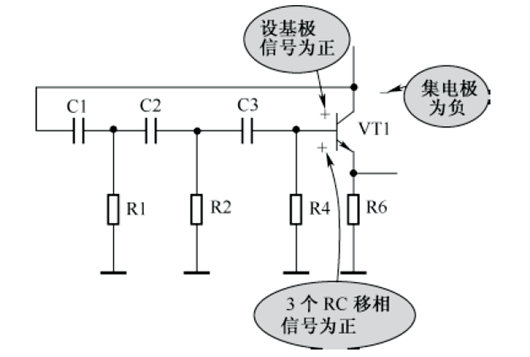
RC正弦波振荡电路
RC正弦波振荡电路 RC正弦波振荡电路又称文氏电桥振荡电路,可以设计频率为f1/2πRC的正弦波发生器。 RC正弦波振荡电路设计:50Hz,振幅为3.47V 电路分析: 1.起振条件取决于R1, R4,R2与1N4148并联电阻(下面简称Rf&#…...
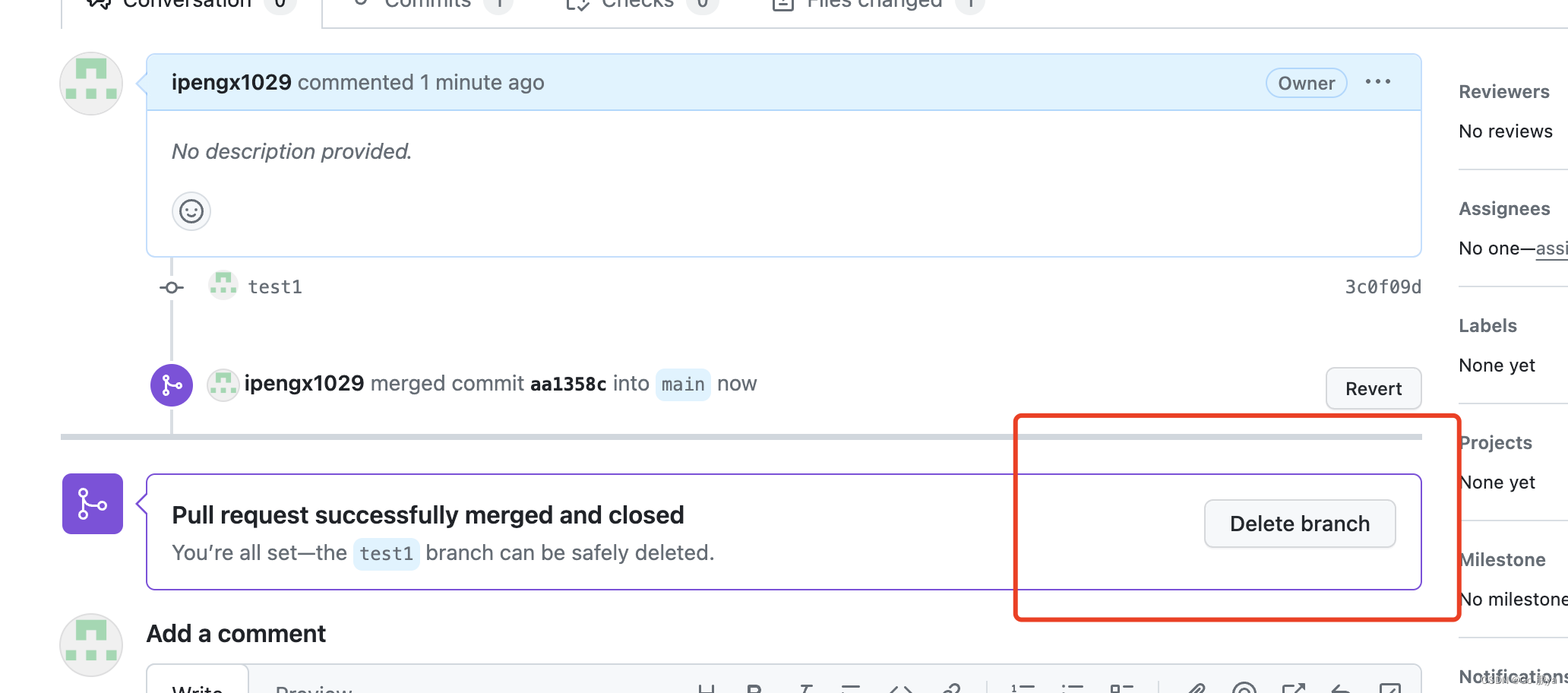
【Git学习笔记】提交PR
step1 克隆一个仓库 git clone .....step2 创建一个分支 (Creating a branch) # 创建并切换到本地新分支,分支的命名尽量简洁,并与解决的问题相关 git checkout -b delete-unused-linkstep3 做出修改 (Make changes) step4 提交修改 # 保存本地修…...

线程池的相关参数
在Java中线程池是一种池化技术,用于管理和复用线程,提高线程的利用率和性能。下面是一些常见的线程池的参数及其解释: 一:线程池的七大参数 public ThreadPoolExecutor(int corePoolSize,int maximumPoolSize,long keepAliveTim…...

图书推荐||Word文稿之美
让你的文档从平凡到出众! 本书内容 《Word文稿之美》是一本全面介绍Word排版技巧和应用的实用指南。从初步认识数字排版到高效利用模板、图文配置和表格与图表的排版技巧,再到快速修正错误和保护文件,全面系统地讲解数字排版的技术和能力&…...
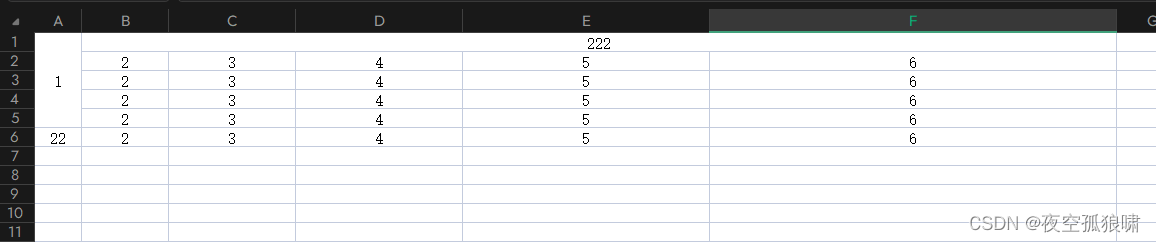
前端导出word文件的多种方式、前端导出excel文件
文章目录 纯前借助word模板端导出word文件 (推荐)使用模板导出 前端通过模板字符串导出word文件前端导出 excel文件,node-xlsx导出文件,行列合并 纯前借助word模板端导出word文件 (推荐) 先看效果…...

Linux和Windows操作系统在腾讯云幻兽帕鲁服务器上的内存占用情况如何?
Linux和Windows操作系统在腾讯云幻兽帕鲁服务器上的内存占用情况如何? 对于Linux操作系统,有用户分享了个人最佳实践来解决内存问题,包括使用Linux脚本让服务器每天重启一次,以及建议在不需要时尽量减少虚拟内存的使用。此外&…...
腾讯云4核8G的云服务器性能水平?使用场景说明
腾讯云4核8G服务器适合做什么?搭建网站博客、企业官网、小程序、小游戏后端服务器、电商应用、云盘和图床等均可以,腾讯云4核8G服务器可以选择轻量应用服务器4核8G12M或云服务器CVM,轻量服务器和标准型CVM服务器性能是差不多的,轻…...
1_SQL
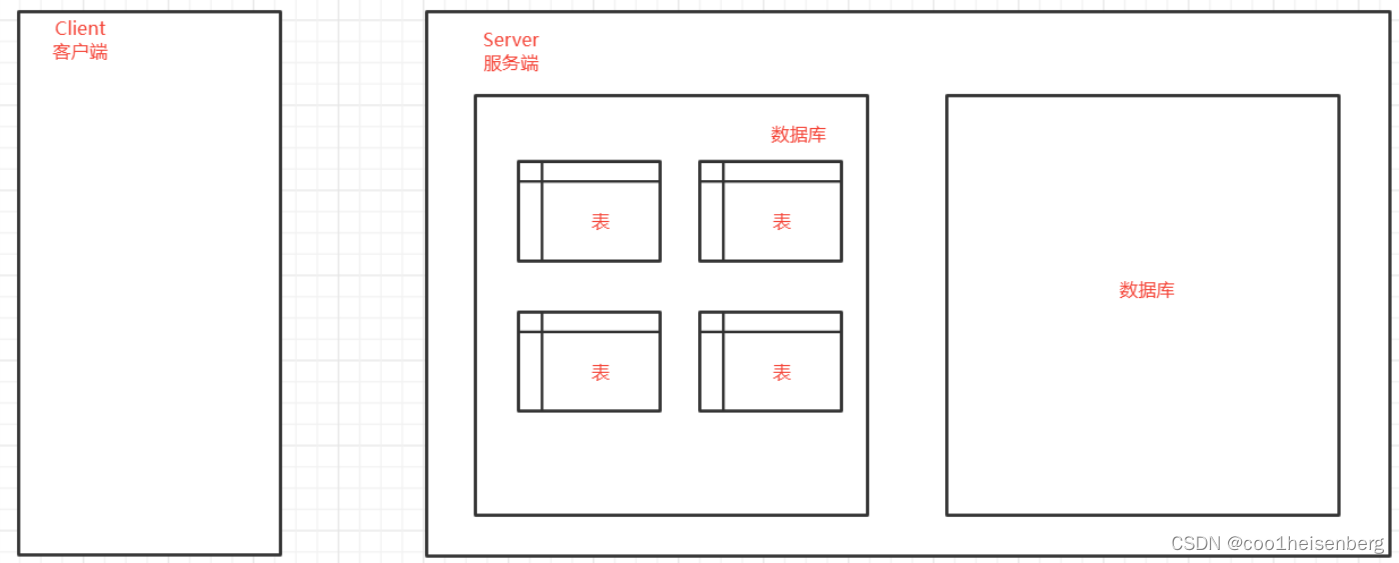
文章目录 前端复习SQL数据库的分类关系型数据库非关系型数据库(NoSQL) 数据库的构成软件架构MySQL内部数据组织方式 SQL语言登录数据库数据库操作查看库创建库删除库修改库 数据库中表的操作选择数据库创建表删除表查看表修改表 数据库中数据的操作添加数…...
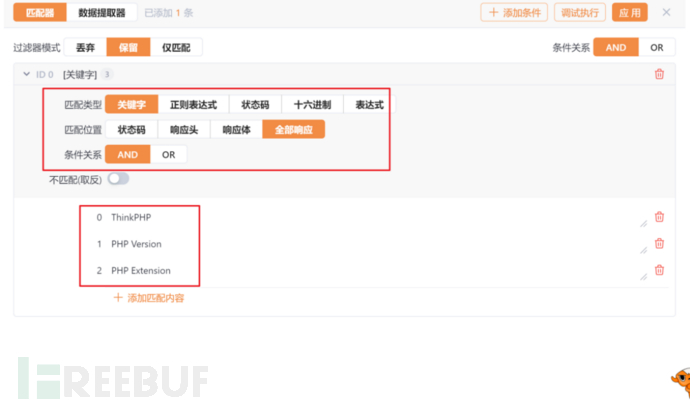
PoC免写攻略
在网络安全领域,PoC(Proof of Concept)起着重要的作用,并且在安全研究、漏洞发现和漏洞利用等方面具有重要的地位。攻击方视角下,常常需要围绕 PoC 做的大量的工作。常常需要从手动测试开始编写 PoC,再到实…...

c1-周考2
c1-第二周 9月-技能1.一个岛上有两种神奇动物,其中神奇鸟类2个头3只脚,神奇兽类3个头8只脚。游客在浓雾中看到一群动物,共看到35个头和110只脚,求可能的鸟类和兽类的只数2.构建一个长度为5的数组,并且实现下列要求3.构…...
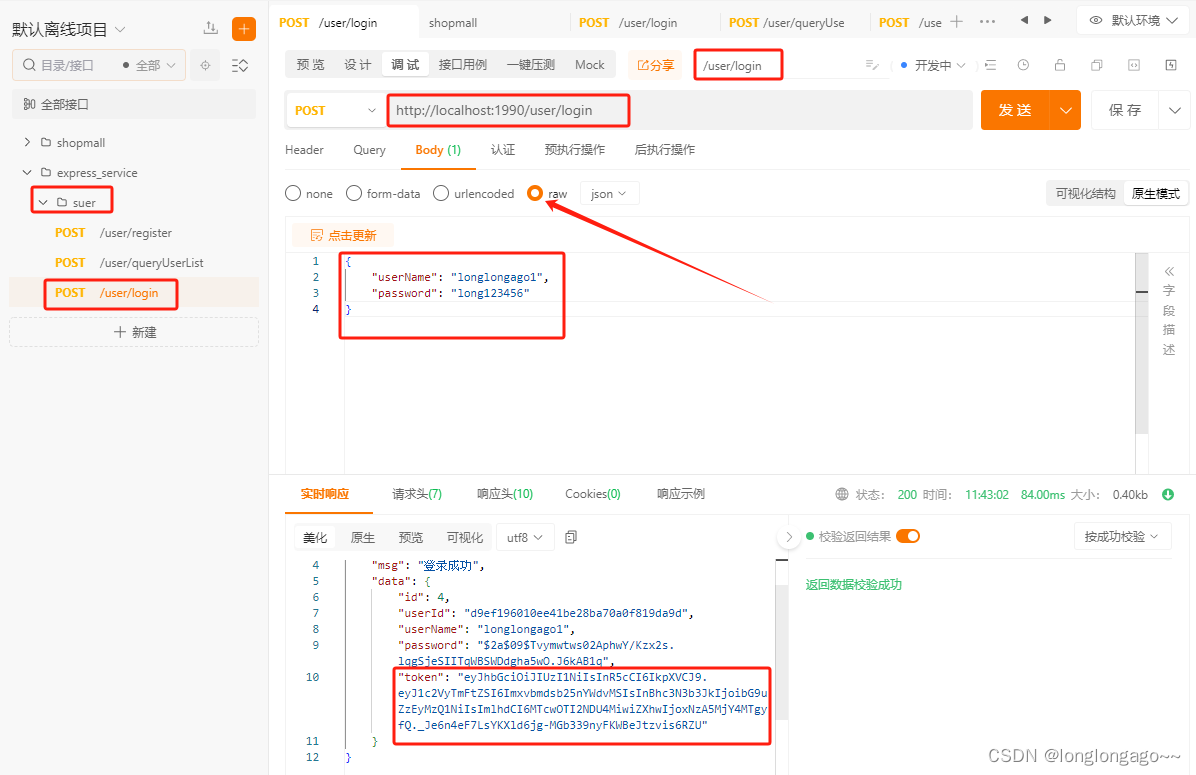
express+mysql+vue,从零搭建一个商城管理系统7--文件上传,大文件分片上传
提示:学习express,搭建管理系统 文章目录 前言一、安装multer,fs-extra二、新建config/upload.js三、新建routes/upload.js四、修改routes下的index.js五、修改index.js六、新建上传文件test.html七、开启jwt验证token,通过login接…...
markdown的使用(Typora)
文章目录 markdown的使用(Typora)一.标题二.段落格式2.1 换行2.2 分割线2.3 字体2.4 上下标2.5 脚注2.6 改变字体颜色 三.列表3.1 无序列表3.2 有序列表3.3 列表嵌套3.4 任务列表 四.区块五.代码显示5.1 行内代码5.2 代码块 六.链接七.图片八.表格九.表情符号大纲十、流程图10.…...
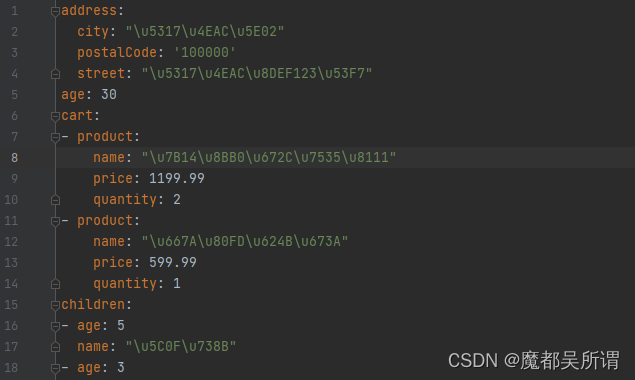
【python】json转成成yaml中文编码异常显示成:\u5317\u4EAC\u8DEF123\u53F7
姊妹篇:【python】json转成成yaml json数据 {"name": "张三","age": 30,"isMarried": false,"children": [{"name": "小王","age": 5},{"name": "小李",&qu…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
