练习2-线性回归迭代(李沐函数简要解析)
环境:再练习1中
视频链接:https://www.bilibili.com/video/BV1PX4y1g7KC/?spm_id_from=333.999.0.0
代码与详解
数据库
numpy 数据处理处理
torch.utils 数据加载与数据
d2l 专门的库
nn 包含各种层与激活函数
import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l
from torch import nn
生成数据集
w=torch.tensor([2,-3.4]) 生成一维两个向量的张量
features,labels=d2l.synthetic_data(w,b,nume) 生成nume个w为权重,b为偏置的数据
w=torch.tensor([2,-3.4])
b=4.2
features,labels=d2l.synthetic_data(w,b,100)
定义对数据集的读取
data.TensorDataset(*data_arrays) 将多个张量合并为一个 通常用于合并特征值与标签 data_arrays=(features,labels)
data.DataLoader(dataset,batchsize,shuffle=true)每次根据上一个函数返回的对象读取batchsize个值 并打乱数据
def load_arrays(data_arrays,batch_size,is_train=True):dataset=data.TensorDataset(*data_arrays)return data.DataLoader(dataset,batch_size,is_train)
定义数据加载器 并 调用
next(iter(已初始化的数据加载器)) 重新调用数据加载器
batch_size=10
data_iter=load_arrays((features,labels),batch_size)
next(iter(data_iter))
定义模型
定义为线性模型且只有一层
nn.Sequential() 用于包装层
nn.linear(2,1) 用于定义两输入一输出的线性层
net=nn.Sequential(nn.Linear(2,1))
初始化参数 w,b,lr,epoch,batch_size
net[0].weight.data.normal 正态分布
net[0].bias.data.fill_(0) b赋值
net[0].weight.data.normal_(0,0.01)
net[0].bias.data.fill_(0)
定义损失函数 平方误差
nn.MSELoss()
Loss=nn.MSELoss()
优化算法 小批量梯度下降 torch.optim.SGD(net.parameters(), lr=0.03)
trainer=torch.optim.SGD(net.parameters(),lr=0.03)
训练
epochs=3
for epoch in range(epochs):for X,y in data_iter:l=Loss(net(X),y)# 将梯度清零 trainer.zero_grad()# 反向传播l.backward()#更新参数trainer.step()l=Loss(net(features),labels)print(f'epoch {epoch + 1}, loss {l:f}')
相关函数与组成部分
定义模型
定义线性回归模型
from torch import nn
net=nn.Sequential(nn.Linear(2,1))
为模型赋值
w,b正态分布
net[0].weight.data.normal_(0,0.01)
net[0].bias.data.fill_(0)
定义损失函数
Loss=nn.MSELoss()
定义优化算法
trainer = torch.optim.SGD(net.parameters(),lr=0.03)
(训练与反向传播不太了解)
相关的Python语法
def 函数名(变量=True):return for epoch in range(epochs):
相关文章:
)
练习2-线性回归迭代(李沐函数简要解析)
环境:再练习1中 视频链接:https://www.bilibili.com/video/BV1PX4y1g7KC/?spm_id_from333.999.0.0 代码与详解 数据库 numpy 数据处理处理 torch.utils 数据加载与数据 d2l 专门的库 nn 包含各种层与激活函数 import numpy as np import torch from torch.utils import da…...

人像背景分割SDK,智能图像处理
美摄科技人像背景分割SDK解决方案:引领企业步入智能图像处理新时代 随着科技的不断进步,图像处理技术已成为许多行业不可或缺的一部分。为了满足企业对于高质量、高效率人像背景分割的需求,美摄科技推出了一款领先的人像背景分割SDK…...
100M服务器能同时容纳多少人访问
100M服务器的并发容纳人数会受到多种因素的影响,这些因素包括单个用户的平均访问流量大小、每个用户的平均访问页面数、并发用户比例、服务器和网络的流量利用率以及服务器自身的处理能力。 点击以下任一云产品链接,跳转后登录,自动享有所有…...
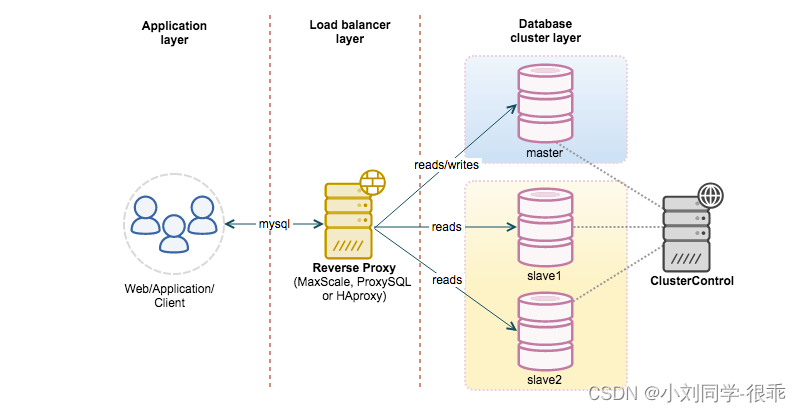
Mysql 的高可用详解
Mysql 高可用 复制 复制是解决系统高可用的常见手段。其思路就是:不要把鸡蛋都放在一个篮子里。 复制解决的基本问题是让一台服务器的数据与其他服务器保持同步。一台主库的数据可以同步到多台备库上,备库本身也可以被配置成另外一台服务器的主库。主…...
)
Acwing枚举、模拟与排序(一)
连号区间数 原题链接:https://www.acwing.com/problem/content/1212/ 初始最小值和最大值的依据是题目给出的数据范围。只要在数据范围之外就可以。 连号的时候,相邻元素元素之间,差值为1。那么区间右边界和左边界,的值的差&#…...

MySQL的主从同步原理
MySQL的主从同步(也称为复制)是一种数据同步技术,用于将一个MySQL服务器(主服务器)上的数据和变更实时复制到另一个或多个MySQL服务器(从服务器)。这项技术支持数据备份、读写分离、故障恢复等多…...
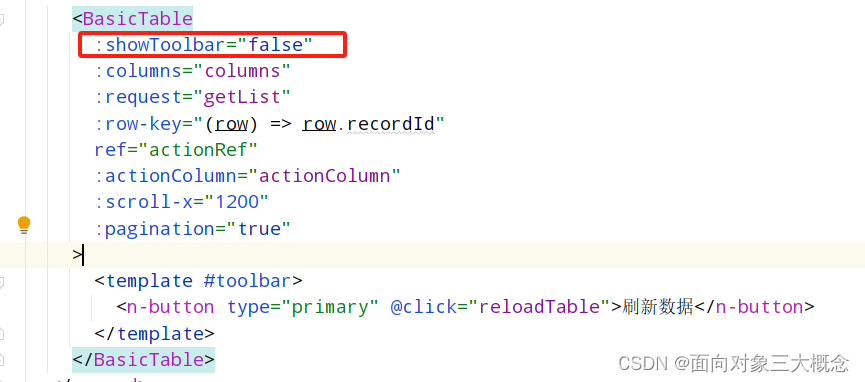
naive-ui-admin 表格去掉工具栏toolbar
使用naive-ui-admin的时候,有时候不需要显示工具栏,工具栏太占地方了。 1.在src/components/Table/src/props.ts 里面添加属性 showToolbar 默认显示,在不需要的地方传false。也可以默认不显示 ,这个根据需求来。 2.在src/compo…...

C++之结构体
结构体 //一、结构体的概念、定义和使用 // 概念:结构体属于用户自定义的数据类型,允许用户存储不同的数据类型 #include<iostream> using namespace std; #include<string> //1.创建学生数据类型:学生包括(姓名&am…...
)
分布式ID选型对比(1)
常见的几种ID生成方式对比: 种类 全局唯一 高性能 高可用 趋势递增 中心服务 缺点 UUID 是 高(本地生成,(无网络开销) 低(无序,不适用) 否 否 无序、字符串 数据库自增 单表唯一 中 中(宕机就会使业务服务中断) 是 否 安全性差,能猜出来规律 对于分库分表场景无法唯一 数据库自…...

T-SQL 高阶语法之存储过程
一:存储过程概念 预先存储好的sql程序,通过名称和参数进行执行,供应程序去调用,也可以有返回结果,存储过程可以包含sql语句 可以包含流程控制、逻辑语句等。 二:存储过程的优点 执行速度更快 允许模块化…...
解决鸿蒙模拟器卡顿的问题
缘起 最近在学习鸿蒙的时候,发现模拟器非常卡,不要说体验到鸿蒙的丝滑,甚至到严重影响使用的程度。 根据我开发Android的经验和在论坛翻了一圈,最终总结出了以下几个方案。 创建模拟器 1、在DevEco Virtual Device Configurat…...

【LeetCode每日一题】【BFS模版与例题】863.二叉树中所有距离为 K 的结点
BFS的基本概念 BFS 是广度优先搜索(Breadth-First Search)的缩写,是一种图遍历算法。它从给定的起始节点开始,逐层遍历图中的节点,直到遍历到目标节点或者遍历完所有可达节点。 BFS 算法的核心思想是先访问当前节点的…...

设计模式-结构模式-装饰模式
装饰模式(Decorator Pattern):动态地给一个对象增加一些额外的职责,就增加对象功能来说,装饰模式比生成子类实现更为灵活。装饰模式是一种对象结构型模式。 //首先,定义一个组件接口: public in…...
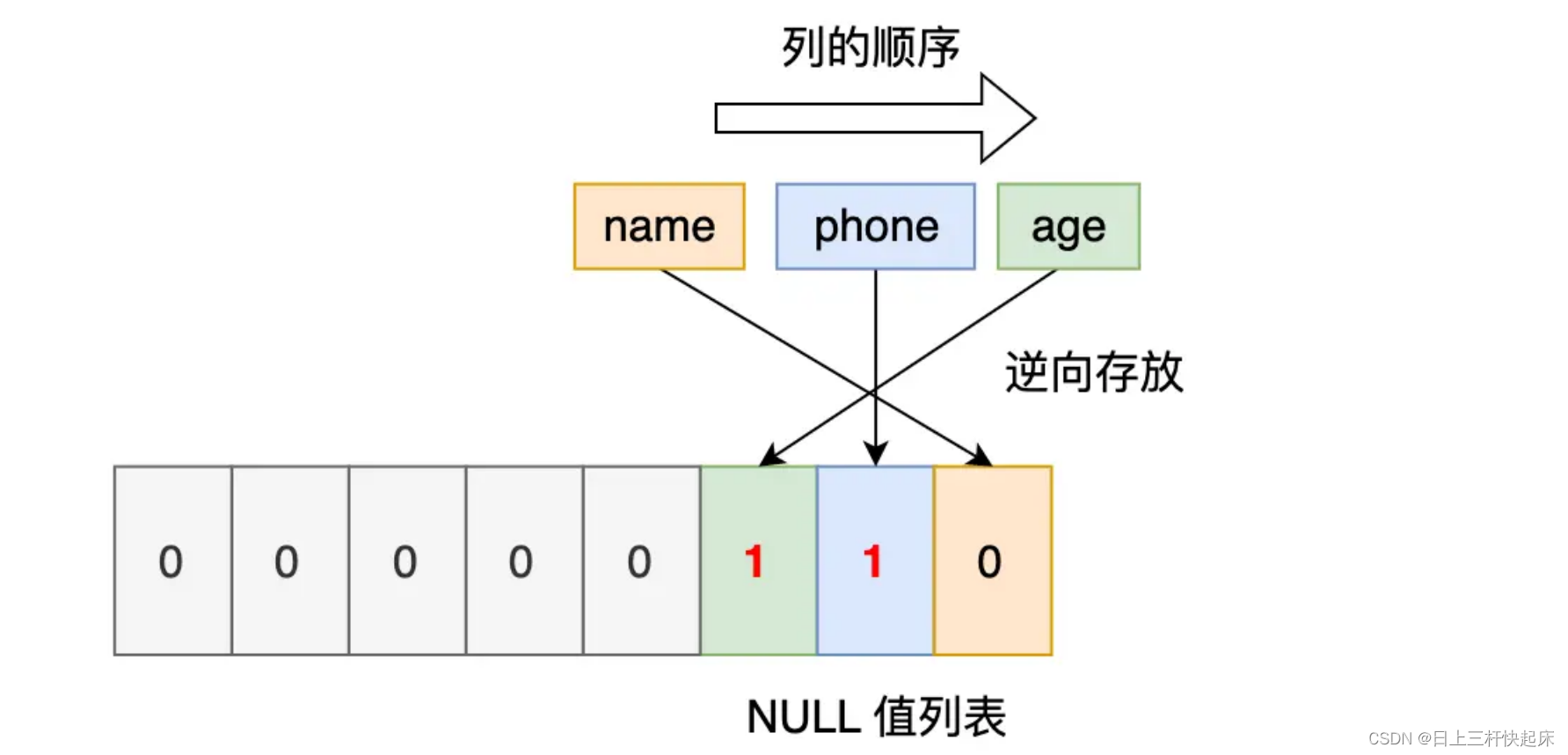
MySQL:一行记录如何
1、表空间文件结构 表空间由段「segment」、区「extent」、页「page」、行「row」组成,InnoDB存储引擎的逻辑存储结构大致如下图: 行 数据库表中的记录都是按「行」进行存放的,每行记录根据不同的行格式,有不同的存储结构。 页…...

‘grafana.ini‘ is read only ‘defaults.ini‘ is read only
docker安装grafana 关闭匿名登录情况下的免密登录遇到问题 grafana.ini is read only defaults.ini is read only 参考回答(Grafana.ini giving me the creeps - #2 by bartweemaels - Configuration - Grafana Labs Community Forums) 正确启动脚本 …...
博途PLC 面向对象系列之“输送带控制功能块“(SCL代码)
这篇是面向对象系列之"输送带功能块"的封装,面向对象是系列文章,相关链接如下: 1、面向对象系列之找"对象" https://rxxw-control.blog.csdn.net/article/details/136150027https://rxxw-control.blog.csdn.net/article/details/1361500272、面向对象…...
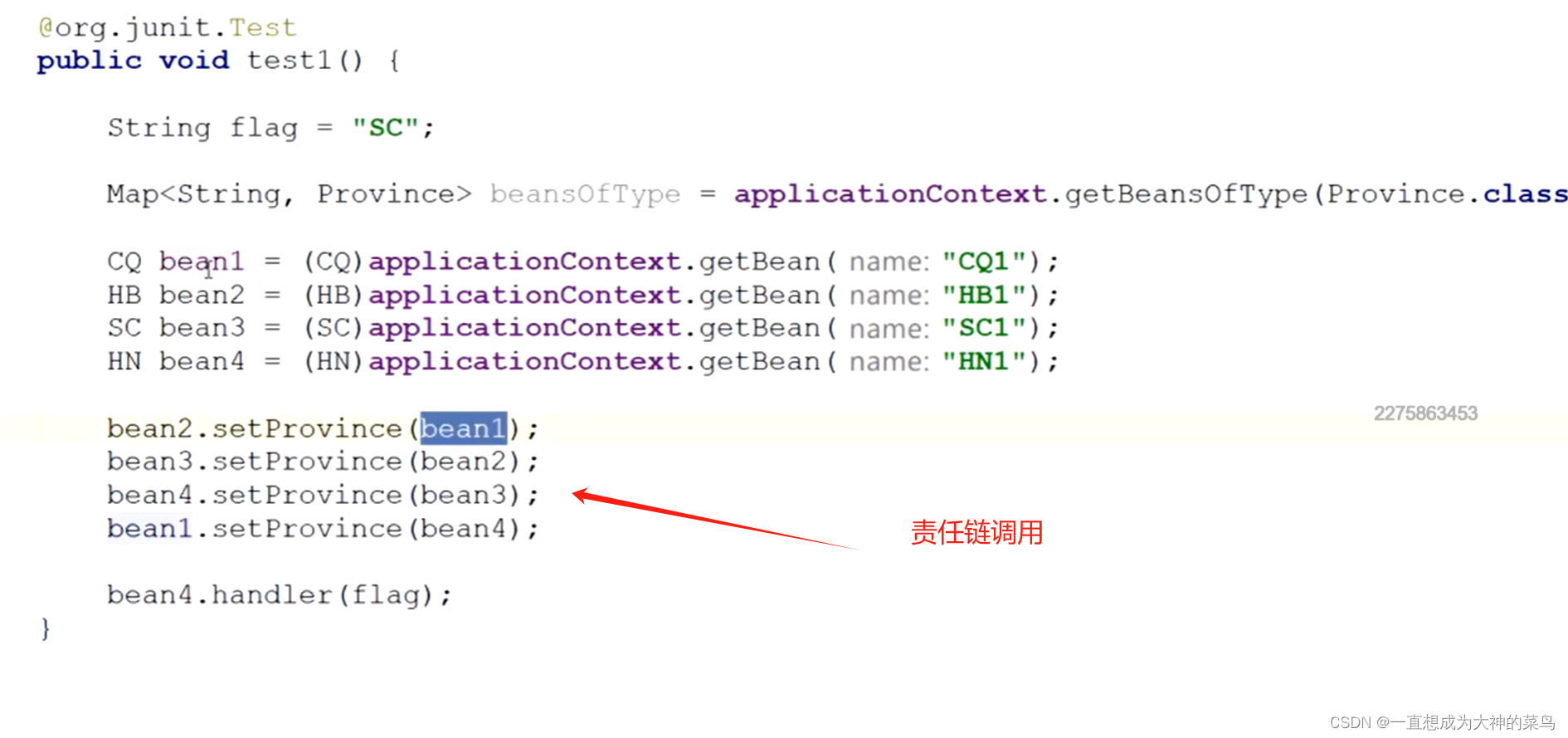
2024-02学习笔记
1.当我们向Set集合中添加一个已经存在的元素时 当我们向Set集合中添加一个已经存在的元素时,Set集合会如何处理呢?实际上,Set集合不会将重复的元素添加到集合中。当我们向Set集合中添加一个元素时,Set集合会首先判断该元素是否已…...

最新消息:英特尔宣布成立全新独立运营的FPGA公司——Altera
今天,英特尔宣布成立全新独立运营的FPGA公司——Altera(2015年6月Intel以 167 亿美元的价格,收购FPGA厂商Altera)。首席执行官Sandra Rivera和首席运营官Shannon Poulin分享展示其在超过550亿美元的市场中保持领先性的战略规划&am…...
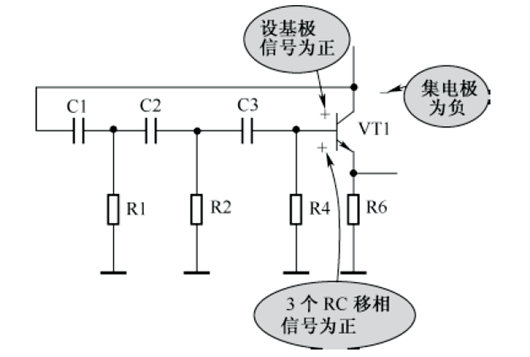
RC正弦波振荡电路
RC正弦波振荡电路 RC正弦波振荡电路又称文氏电桥振荡电路,可以设计频率为f1/2πRC的正弦波发生器。 RC正弦波振荡电路设计:50Hz,振幅为3.47V 电路分析: 1.起振条件取决于R1, R4,R2与1N4148并联电阻(下面简称Rf&#…...
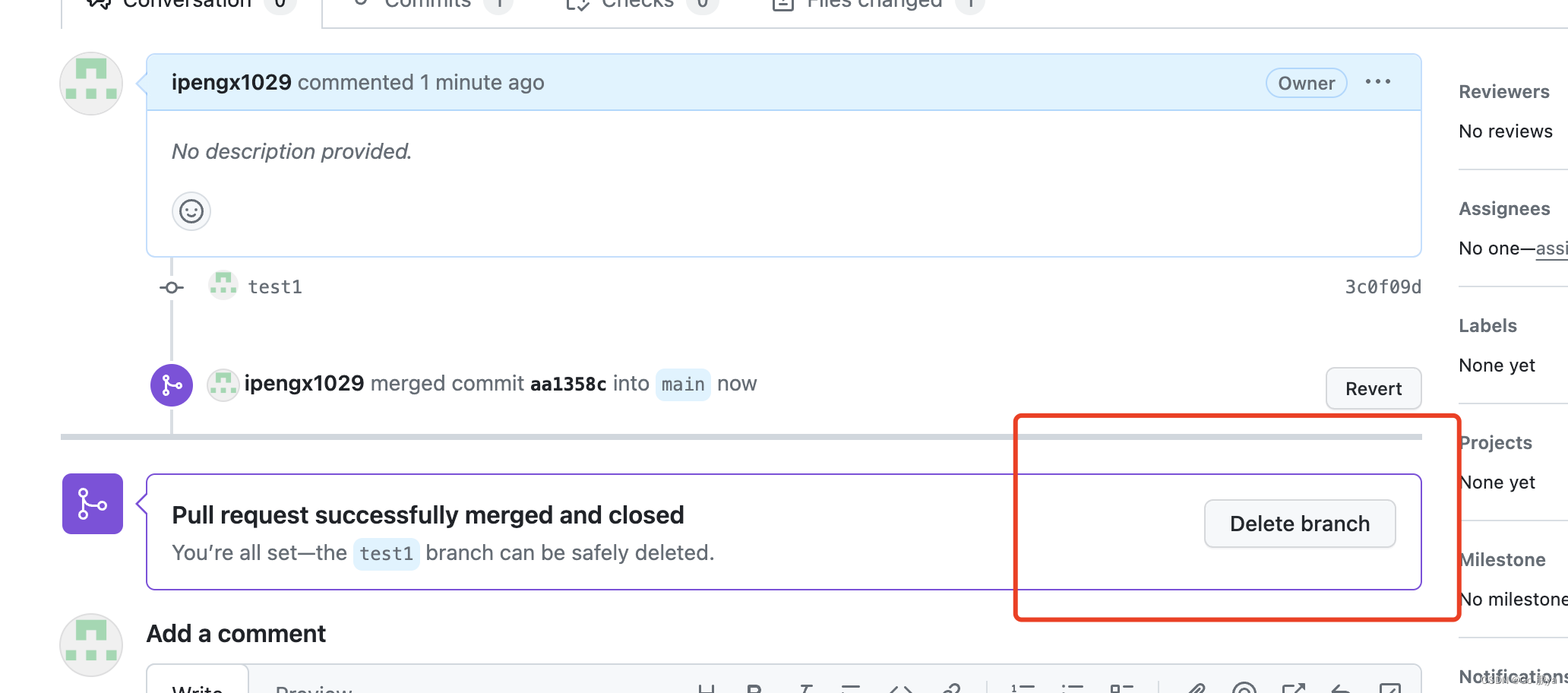
【Git学习笔记】提交PR
step1 克隆一个仓库 git clone .....step2 创建一个分支 (Creating a branch) # 创建并切换到本地新分支,分支的命名尽量简洁,并与解决的问题相关 git checkout -b delete-unused-linkstep3 做出修改 (Make changes) step4 提交修改 # 保存本地修…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...
