2024年FPGA可以进吗
2024年,IC设计FPGA行业仍有可能是一个极具吸引力和活力的行业,主要原因包括:
1. 技术发展趋势:随着5G、人工智能、物联网、自动驾驶、云计算等高新技术的快速发展和广泛应用,对集成电路尤其是高性能、低功耗、定制化芯片的需求将持续攀升,这为IC设计行业提供了丰富的市场机遇。
2. 政策导向与支持:多个国家和地区政府都把集成电路产业作为战略新兴产业加以重点扶持,特别是在中国,政府提出了明确的目标和一系列政策支持措施,旨在提高芯片自给率和本土创新能力,为IC设计行业创造了有利的发展环境。
3. 市场增长:尽管半导体行业存在周期性波动,但长期来看,全球半导体市场的总体趋势仍然是上升的,特别是中国市场对于集成电路的内需逐年增大,预计市场规模将持续扩大。
4. 人才需求:随着行业的发展,对IC设计人才的需求也将持续增长。虽然行业对专业技能要求较高,但对于有意转行或新加入该行业的人才而言,只要具备相应的技术基础和持续学习的能力,依然有机会进入这一行业。
5. 技术创新驱动:新型封装技术、先进制程节点的研发以及异构集成等技术的创新,都将带动IC设计行业的革新与发展,为新入行者提供了广阔的创新空间。不过,考虑到行业竞争激烈和技术更新快速,潜在进入者需要密切关注行业动态,评估自身的技能储备和学习能力,并做好充分的职业规划。
此外,由于IC设计行业存在一定的技术壁垒和研发投入风险,企业和个人都需要在决策时充分权衡这些因素。总的来说,如果具备足够的准备和条件,2024年进入IC设计行业依然是一个可行的选择。
根据之前的信息,IC行业在2024年间仍然存在较大的人才缺口,这是因为芯片行业的复杂度增加以及对高质量芯片需求的增长。国家政策的支持和行业发展也可能继续推动对IC工程师的需求。
为了准确了解2024年的最新招聘情况和薪资待遇,请关注小编。
这里有一个入口:FPGA学习资料免费领!
相关文章:

2024年FPGA可以进吗
2024年,IC设计FPGA行业仍有可能是一个极具吸引力和活力的行业,主要原因包括: 1. 技术发展趋势:随着5G、人工智能、物联网、自动驾驶、云计算等高新技术的快速发展和广泛应用,对集成电路尤其是高性能、低功耗、定制化芯…...
小程序图形:echarts-weixin 入门使用
去官网下载整个项目: https://github.com/ecomfe/echarts-for-weixin 拷贝ec-canvs文件夹到小程序里面 index.js里面的写法 import * as echarts from "../../components/ec-canvas/echarts" const app getApp(); function initChart(canvas, width, h…...

百度百科人物创建要求是什么?
百度百科作为我国最大的中文百科全书,其收录的人物词条要求严谨、客观、有权威性。那么,如何撰写一篇高质量的人物词条呢?本文伯乐网络传媒将从内容要求、注意事项以及创建流程与步骤三个方面进行详细介绍。 一、内容要求 1. 基本信息&#…...
)
练习2-线性回归迭代(李沐函数简要解析)
环境:再练习1中 视频链接:https://www.bilibili.com/video/BV1PX4y1g7KC/?spm_id_from333.999.0.0 代码与详解 数据库 numpy 数据处理处理 torch.utils 数据加载与数据 d2l 专门的库 nn 包含各种层与激活函数 import numpy as np import torch from torch.utils import da…...

人像背景分割SDK,智能图像处理
美摄科技人像背景分割SDK解决方案:引领企业步入智能图像处理新时代 随着科技的不断进步,图像处理技术已成为许多行业不可或缺的一部分。为了满足企业对于高质量、高效率人像背景分割的需求,美摄科技推出了一款领先的人像背景分割SDK…...
100M服务器能同时容纳多少人访问
100M服务器的并发容纳人数会受到多种因素的影响,这些因素包括单个用户的平均访问流量大小、每个用户的平均访问页面数、并发用户比例、服务器和网络的流量利用率以及服务器自身的处理能力。 点击以下任一云产品链接,跳转后登录,自动享有所有…...
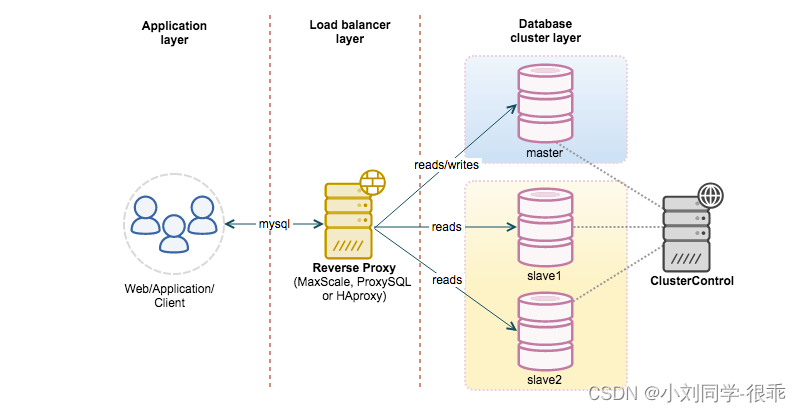
Mysql 的高可用详解
Mysql 高可用 复制 复制是解决系统高可用的常见手段。其思路就是:不要把鸡蛋都放在一个篮子里。 复制解决的基本问题是让一台服务器的数据与其他服务器保持同步。一台主库的数据可以同步到多台备库上,备库本身也可以被配置成另外一台服务器的主库。主…...
)
Acwing枚举、模拟与排序(一)
连号区间数 原题链接:https://www.acwing.com/problem/content/1212/ 初始最小值和最大值的依据是题目给出的数据范围。只要在数据范围之外就可以。 连号的时候,相邻元素元素之间,差值为1。那么区间右边界和左边界,的值的差&#…...

MySQL的主从同步原理
MySQL的主从同步(也称为复制)是一种数据同步技术,用于将一个MySQL服务器(主服务器)上的数据和变更实时复制到另一个或多个MySQL服务器(从服务器)。这项技术支持数据备份、读写分离、故障恢复等多…...
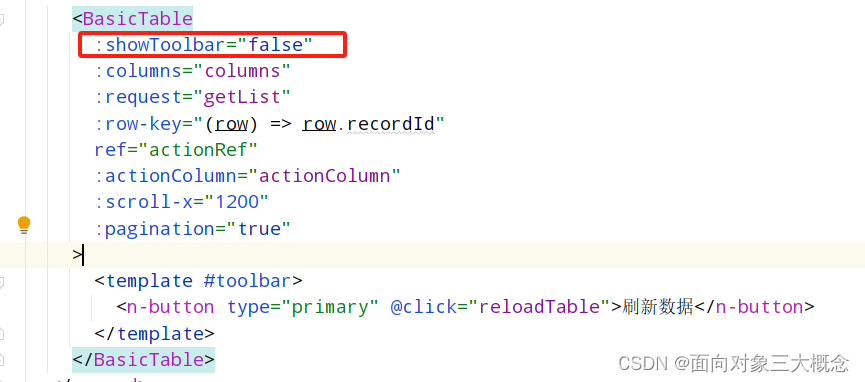
naive-ui-admin 表格去掉工具栏toolbar
使用naive-ui-admin的时候,有时候不需要显示工具栏,工具栏太占地方了。 1.在src/components/Table/src/props.ts 里面添加属性 showToolbar 默认显示,在不需要的地方传false。也可以默认不显示 ,这个根据需求来。 2.在src/compo…...

C++之结构体
结构体 //一、结构体的概念、定义和使用 // 概念:结构体属于用户自定义的数据类型,允许用户存储不同的数据类型 #include<iostream> using namespace std; #include<string> //1.创建学生数据类型:学生包括(姓名&am…...
)
分布式ID选型对比(1)
常见的几种ID生成方式对比: 种类 全局唯一 高性能 高可用 趋势递增 中心服务 缺点 UUID 是 高(本地生成,(无网络开销) 低(无序,不适用) 否 否 无序、字符串 数据库自增 单表唯一 中 中(宕机就会使业务服务中断) 是 否 安全性差,能猜出来规律 对于分库分表场景无法唯一 数据库自…...

T-SQL 高阶语法之存储过程
一:存储过程概念 预先存储好的sql程序,通过名称和参数进行执行,供应程序去调用,也可以有返回结果,存储过程可以包含sql语句 可以包含流程控制、逻辑语句等。 二:存储过程的优点 执行速度更快 允许模块化…...
解决鸿蒙模拟器卡顿的问题
缘起 最近在学习鸿蒙的时候,发现模拟器非常卡,不要说体验到鸿蒙的丝滑,甚至到严重影响使用的程度。 根据我开发Android的经验和在论坛翻了一圈,最终总结出了以下几个方案。 创建模拟器 1、在DevEco Virtual Device Configurat…...

【LeetCode每日一题】【BFS模版与例题】863.二叉树中所有距离为 K 的结点
BFS的基本概念 BFS 是广度优先搜索(Breadth-First Search)的缩写,是一种图遍历算法。它从给定的起始节点开始,逐层遍历图中的节点,直到遍历到目标节点或者遍历完所有可达节点。 BFS 算法的核心思想是先访问当前节点的…...

设计模式-结构模式-装饰模式
装饰模式(Decorator Pattern):动态地给一个对象增加一些额外的职责,就增加对象功能来说,装饰模式比生成子类实现更为灵活。装饰模式是一种对象结构型模式。 //首先,定义一个组件接口: public in…...
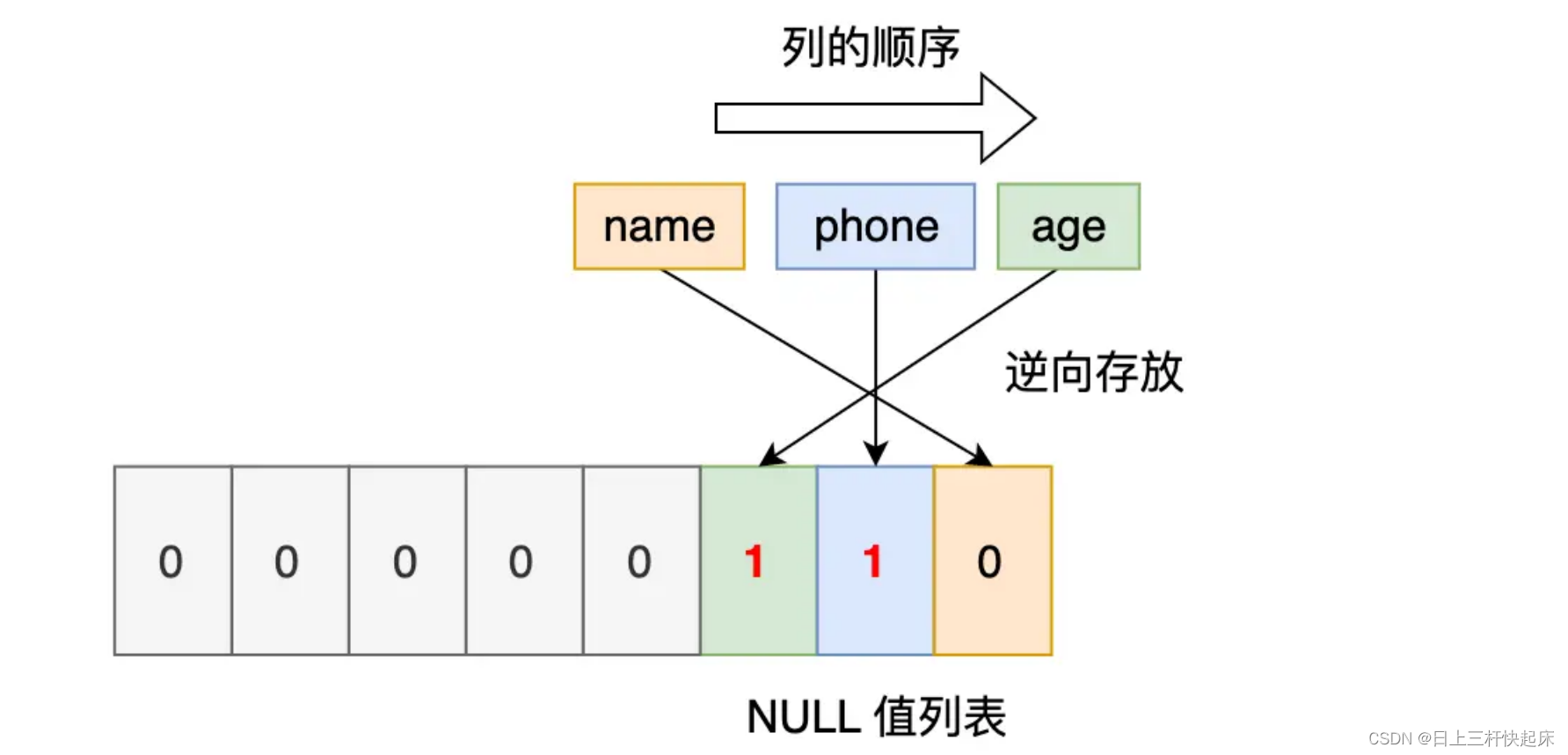
MySQL:一行记录如何
1、表空间文件结构 表空间由段「segment」、区「extent」、页「page」、行「row」组成,InnoDB存储引擎的逻辑存储结构大致如下图: 行 数据库表中的记录都是按「行」进行存放的,每行记录根据不同的行格式,有不同的存储结构。 页…...

‘grafana.ini‘ is read only ‘defaults.ini‘ is read only
docker安装grafana 关闭匿名登录情况下的免密登录遇到问题 grafana.ini is read only defaults.ini is read only 参考回答(Grafana.ini giving me the creeps - #2 by bartweemaels - Configuration - Grafana Labs Community Forums) 正确启动脚本 …...
博途PLC 面向对象系列之“输送带控制功能块“(SCL代码)
这篇是面向对象系列之"输送带功能块"的封装,面向对象是系列文章,相关链接如下: 1、面向对象系列之找"对象" https://rxxw-control.blog.csdn.net/article/details/136150027https://rxxw-control.blog.csdn.net/article/details/1361500272、面向对象…...
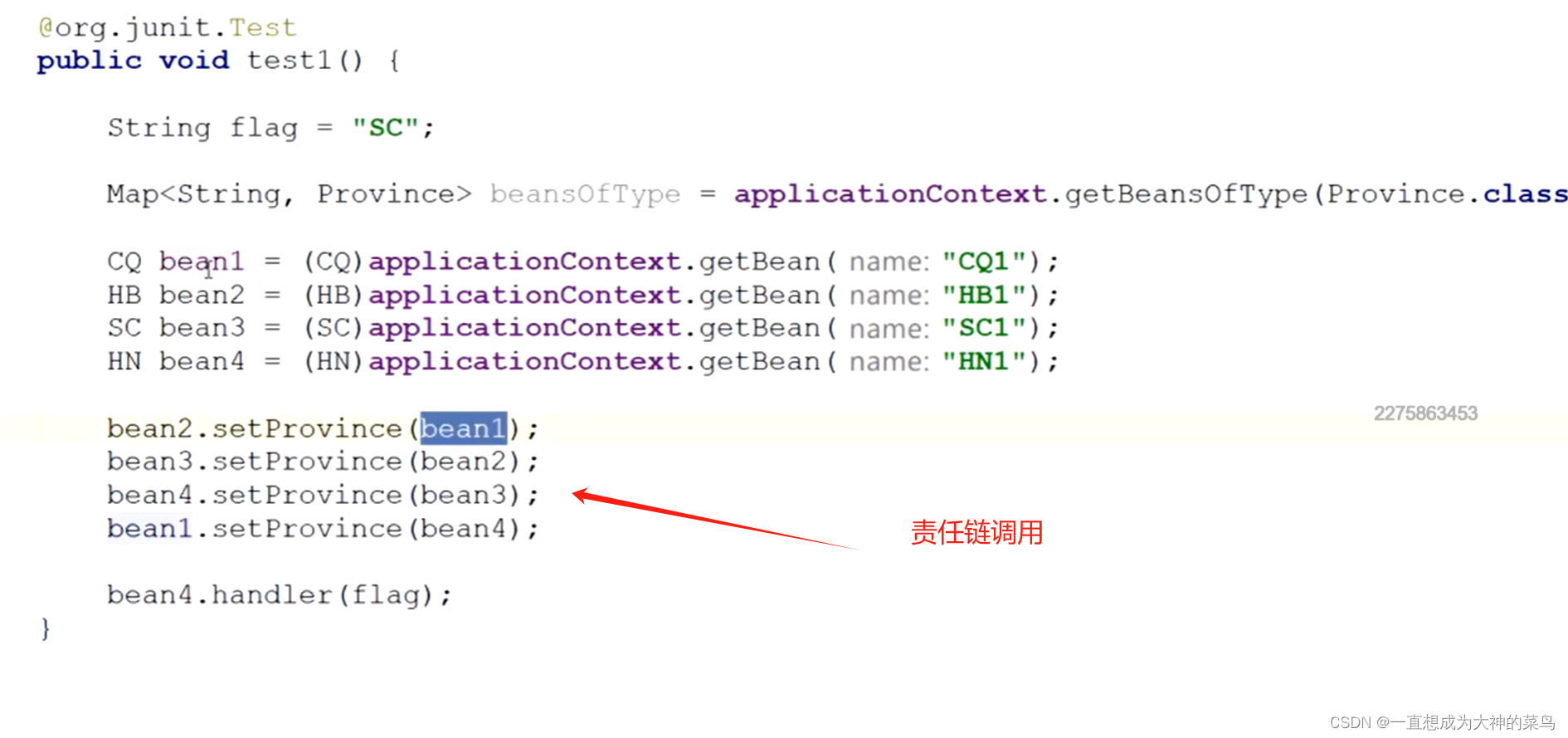
2024-02学习笔记
1.当我们向Set集合中添加一个已经存在的元素时 当我们向Set集合中添加一个已经存在的元素时,Set集合会如何处理呢?实际上,Set集合不会将重复的元素添加到集合中。当我们向Set集合中添加一个元素时,Set集合会首先判断该元素是否已…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...
