LeetCode——二叉树(Java)
二叉树
- 简介
- [简单] 144. 二叉树的前序遍历、94. 二叉树的中序遍历、145. 二叉树的后序遍历
- 二叉树层序遍历
- [中等] 102. 二叉树的层序遍历
- [中等] 107. 二叉树的层序遍历 II
- [中等] 199. 二叉树的右视图
- [简单] 637. 二叉树的层平均值
- [中等] 429. N 叉树的层序遍历
- [中等] 515. 在每个树行中找最大值
- [中等] 116. 填充每个节点的下一个右侧节点指针、[中等]117. 填充每个节点的下一个右侧节点指针 II
- [简单] 104. 二叉树的最大深度
- [简单] 111. 二叉树的最小深度
- [简单] 226. 翻转二叉树
- [简单] 101. 对称二叉树
- [简单] 100. 相同的树
- [简单] 572. 另一棵树的子树
- [简单] 222. 完全二叉树的节点个数
- [简单] 110. 平衡二叉树
- [简单] 257. 二叉树的所有路径
简介
记录一下自己刷题的历程以及代码。写题过程中参考了 代码随想录的刷题路线。会附上一些个人的思路,如果有错误,可以在评论区提醒一下。
涉及:二叉树前中后序遍历、层序遍历、队列Queue、头插法、递归、ArrayList、LinkedList、递归、StringBuilder
[简单] 144. 二叉树的前序遍历、94. 二叉树的中序遍历、145. 二叉树的后序遍历
144. 二叉树的前序遍历
94. 二叉树的中序遍历
145. 二叉树的后序遍历
前中后序遍历可以公用一套递归思路,都是比较经典的模板:
//先序遍历
递归访问(){对节点做操作递归访问(左子树)递归访问(右子树)
}//中序遍历
递归访问(){递归访问(左子树)对节点做操作递归访问(右子树)
}//后序遍历
递归访问(){递归访问(左子树)递归访问(右子树)对节点做操作
}
- 二叉树的前序遍历
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> answer = new ArrayList<>();preorder(root, answer);return answer;}public void preorder(TreeNode root, List<Integer> answer){if(root == null) return;answer.add(root.val);preorder(root.left,answer);preorder(root.right,answer);return;}
}
- 二叉树的中序遍历
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> answer = new ArrayList<>();inorder(root, answer);return answer;}public void inorder(TreeNode root, List<Integer> answer){if(root == null) return;inorder(root.left,answer);answer.add(root.val);inorder(root.right,answer);return;}
}
- 二叉树的后序遍历
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> answer = new ArrayList<>();postorder(root, answer);return answer;}public void postorder(TreeNode root, List<Integer> answer){if(root == null) return;postorder(root.left,answer);postorder(root.right,answer);answer.add(root.val);return;}
}
二叉树层序遍历
[中等] 102. 二叉树的层序遍历
原题链接
经典的BFS
用队列保存树节点,每次统计队列的size(),也就是第n层节点数量。
处理这一层的节点,将其子节点全部加入队列,循环往复到队列为空。
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> ans = new ArrayList<List<Integer>>();Queue<TreeNode> queue = new ArrayDeque<>();if(root == null) return ans;queue.add(root);while(!queue.isEmpty()){List<Integer> nums = new ArrayList<Integer>();int k = queue.size();while(k-- > 0) {TreeNode temp = queue.remove();nums.add(temp.val);if (temp.left != null) queue.add(temp.left);if (temp.right != null) queue.add(temp.right);}ans.add(nums);}return ans;}
}
[中等] 107. 二叉树的层序遍历 II
原题链接
方法①:
与102的最基本的层序遍历相似的逻辑,使用递归的方法把每次ans.add(nums);操作顺序进行了倒序。
class Solution {public List<List<Integer>> levelOrderBottom(TreeNode root) {List<List<Integer>> ans = new ArrayList<List<Integer>>();Queue<TreeNode> queue = new ArrayDeque<>();if(root == null) return ans;queue.add(root);recursion(queue, ans);return ans;}public void recursion(Queue<TreeNode> queue, List<List<Integer>> ans){if(!queue.isEmpty()){List<Integer> nums = new ArrayList<Integer>();int k = queue.size();while(k-- > 0) {TreeNode temp = queue.remove();nums.add(temp.val);if (temp.left != null) queue.add(temp.left);if (temp.right != null) queue.add(temp.right);}recursion(queue, ans);ans.add(nums);}return;}
}
方法②:
使用LinkedList,用头插法的方式构造返回值。(LinkedList底层为链表,头插法比较方便,ArrayList底层是连续存储,头插法复杂度为O(n))
class Solution {public List<List<Integer>> levelOrderBottom(TreeNode root) {List<List<Integer>> ans = new LinkedList<>();Queue<TreeNode> queue = new ArrayDeque<>();if(root == null) return ans;queue.add(root);while(!queue.isEmpty()){List<Integer> nums = new ArrayList<Integer>();int k = queue.size();while(k-- > 0) {TreeNode temp = queue.remove();nums.add(temp.val);if (temp.left != null) queue.add(temp.left);if (temp.right != null) queue.add(temp.right);}ans.add(0, nums);}return ans;}}
[中等] 199. 二叉树的右视图
原题链接
与102的最基本的层序遍历相似的逻辑,构建返回值时每次只把当前层最右边的数加入ans即可。
class Solution {public List<Integer> rightSideView(TreeNode root) {List<Integer> ans = new ArrayList<Integer>();Queue<TreeNode> queue = new ArrayDeque<>();if(root == null) return ans;queue.add(root);while(!queue.isEmpty()){List<Integer> nums = new ArrayList<Integer>();int k = queue.size();while(k-- > 0) {TreeNode temp = queue.remove();nums.add(temp.val);if (temp.left != null) queue.add(temp.left);if (temp.right != null) queue.add(temp.right);}ans.add((nums.get(nums.size()-1)));}return ans;}
}[简单] 637. 二叉树的层平均值
原题链接
class Solution {public List<Double> averageOfLevels(TreeNode root) {Queue<TreeNode> queue = new ArrayDeque<>();List<Double> ans = new ArrayList<>();if(root == null) return ans;queue.add(root);while(!queue.isEmpty()){double num = 0;int k = queue.size();int i = k;while(k-- > 0){TreeNode temp = queue.remove();num += temp.val;if(temp.left != null) queue.add(temp.left);if(temp.right != null) queue.add(temp.right);}ans.add(num / i);}return ans;}
}
[中等] 429. N 叉树的层序遍历
原题链接
class Solution {public List<List<Integer>> levelOrder(Node root) {List<List<Integer>> ans = new ArrayList<List<Integer>>();Queue<Node> queue = new ArrayDeque<>();if(root == null) return ans;queue.add(root);while(!queue.isEmpty()){List<Integer> nums = new ArrayList<Integer>();int k = queue.size();while(k-- > 0) {Node temp = queue.remove();nums.add(temp.val);for(int i = 0; i < temp.children.size(); i++) {queue.add(temp.children.get(i));}}ans.add(nums);}return ans;}
}
[中等] 515. 在每个树行中找最大值
原题链接
class Solution {public List<Integer> largestValues(TreeNode root) {List<Integer> ans = new ArrayList<>();Queue<TreeNode> queue = new ArrayDeque<>();if(root == null) return ans;queue.add(root);while(!queue.isEmpty()){int max = queue.peek().val;int k = queue.size();while(k-- > 0) {TreeNode temp = queue.remove();max = max > temp.val ? max : temp.val;if(temp.left != null) queue.add(temp.left);if(temp.right != null) queue.add(temp.right);}ans.add(max);}return ans;}
}
[中等] 116. 填充每个节点的下一个右侧节点指针、[中等]117. 填充每个节点的下一个右侧节点指针 II
[中等] 116. 填充每个节点的下一个右侧节点指针
[中等]117. 填充每个节点的下一个右侧节点指针 II
方法①:
正常的层序遍历,每层除了最后一个节点之外都对next赋值
class Solution {public Node connect(Node root) {List<Integer> ans = new ArrayList<>();Queue<Node> queue = new ArrayDeque<>();if(root == null) return root;queue.add(root);while(!queue.isEmpty()){int k = queue.size();while(k-- > 0) {Node temp = queue.remove();if(k > 0) {temp.next = queue.peek();}if(temp.left != null) queue.add(temp.left);if(temp.right != null) queue.add(temp.right);}}return root;}
}
方法②:
使用next链接来对同层次节点做遍历,可以省去队列的开销
注意Node引用需要申请在方法外,不能做参数传递,java中都是值传递
class Solution {Node last = null, nextStart = null;public Node connect(Node root) {List<Integer> ans = new ArrayList<>();if(root == null) return root;Node p = root;while(p!=null){if(p.left != null){handle(p.left);}if(p.right != null){handle(p.right);}p = p.next;if(p == null && nextStart != null){p = nextStart;nextStart = null;last = null;}}return root;}public void handle(Node p){if(nextStart == null){nextStart = p;}if(last != null){last.next = p;}last = p;}}
[简单] 104. 二叉树的最大深度
原题链接
方法①:层序遍历
class Solution {public int maxDepth(TreeNode root) {int depth = 0;if(root == null) return depth;Queue<TreeNode> queue = new ArrayDeque<>();queue.add(root);while(!queue.isEmpty()){depth++;int k = queue.size();while(k-- > 0) {TreeNode temp = queue.remove();if (temp.left != null) queue.add(temp.left);if (temp.right != null) queue.add(temp.right);}}return depth;}
}
方法②:递归
树的高度就是 其子树的最大高度 + 1,用在多叉树上也是一样的思路
class Solution {public int maxDepth(TreeNode root) {if(root == null) return 0;int leftDepth = maxDepth(root.left);int rightDepth = maxDepth(root.right);return (leftDepth > rightDepth ? leftDepth : rightDepth) + 1;}
}
[简单] 111. 二叉树的最小深度
原题链接
方法①:层序遍历找左右子树皆空的点即可
class Solution {public int minDepth(TreeNode root) {int depth = 0;if(root == null) return depth;Queue<TreeNode> queue = new ArrayDeque<>();queue.add(root);while(!queue.isEmpty()){depth++;int k = queue.size();while(k-- > 0) {TreeNode temp = queue.remove();if(temp.left == null && temp.right == null) return depth;if (temp.left != null) queue.add(temp.left);if (temp.right != null) queue.add(temp.right);}}return depth;}
}
方法②:递归求解
用递归求解记住需要的是到叶子节点的深度
如果非叶子节点,假设只有单边左子树,右子数应当是找不到叶子节点也就是距离无穷大,可以设置一个Integer.MAX_VALUE做为返回值,这样通过比较,递归的上一层就会获得左子树找到叶子节点的最小距离 + 1
class Solution {public int minDepth(TreeNode root) {if(root == null) return 0;if(root.left == null && root.right == null) return 1;int leftMin = Integer.MAX_VALUE;int rightMin = Integer.MAX_VALUE;if(root.left != null) leftMin = minDepth(root.left);if(root.right != null) rightMin = minDepth(root.right);return (leftMin < rightMin ? leftMin : rightMin) + 1;}
}
[简单] 226. 翻转二叉树
原题链接
前序遍历的基础上每一次遍历节点做翻转操作。
切记前序、后续、层次遍历都可以,但是不可以是中序遍历,因为中序遍历是左 中 右 的顺序,递归调整左子树之后,处理当前节点会把左右子树对调,这样进入右子数递归时其实还是对原先的左子树做操作。
class Solution {public TreeNode invertTree(TreeNode root) {preorder(root);return root;}public void preorder(TreeNode root){if(root == null) return;TreeNode temp = root.left;root.left = root.right;root.right = temp;preorder(root.left);preorder(root.right);return;}
}
[简单] 101. 对称二叉树
原题链接
经典的递归思路,对左右子树做反方向的递归即可,在左子树上做前序遍历,每次递归left的左节点时就去递归right的右节点,递归left的右节点时则递归right的左节点。
class Solution {public boolean isSymmetric(TreeNode root) {if(root == null) return true;TreeNode left = root.left;TreeNode right = root.right;return recursion(left, right);}public boolean recursion(TreeNode left, TreeNode right){if(left == null && right == null)return true;else if(left != null && right != null) {if (left.val != right.val)return false;if (recursion(left.left, right.right) && recursion(left.right, right.left))return true;}return false;}
}
[简单] 100. 相同的树
原题链接
两棵树同频做前序遍历即可,其他遍历方式也是ok的。
class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {return recursion(p, q);}public boolean recursion(TreeNode p, TreeNode q){if(p == null && q == null)return true;else if(p != null && q != null) {if (p.val != q.val)return false;if (recursion(p.left, q.left) && recursion(p.right, q.right))return true;}return false;}
}
[简单] 572. 另一棵树的子树
原题链接
两层递归
①preorder:对root 的前序遍历,找到与subRoot相同值的节点,作为比较的起点②cmprecursion:对root的节点以及subRoot的根节点 做 同频前序遍历对比
class Solution {public boolean isSubtree(TreeNode root, TreeNode subRoot) {if(subRoot == null) return true;if(root == null) return true;return preorder(root, subRoot);}public boolean preorder(TreeNode p, TreeNode q){if(p == null) return false;if(p.val == q.val && cmprecursion(p, q))return true;if(preorder(p.left, q) || preorder(p.right, q)) return true;return false;}public boolean cmprecursion(TreeNode p, TreeNode q){if(p == null && q == null) return true;else if(p != null && q != null){if(p.val != q.val) return false;if(cmprecursion(p.left, q.left) && cmprecursion(p.right, q.right))return true;}return false;}
}
[简单] 222. 完全二叉树的节点个数
原题链接
递归
class Solution {public int countNodes(TreeNode root) {if(root == null) return 0;return countNodes(root.left) + countNodes(root.right) + 1;}
}
[简单] 110. 平衡二叉树
原题链接
递归,后序遍历
用-2标记 以当前节点为根节点的子树非平衡二叉树,在递归中一旦出现-2就层层传递到root,用来标识存在子树为非平衡二叉树
class Solution {public boolean isBalanced(TreeNode root) {if(countDepth(root) == -2) return false;return true;}public int countDepth(TreeNode p){if(p == null) return 0;int leftDepth = countDepth(p.left);int rightDepth = countDepth(p.right);int flag = leftDepth - rightDepth;if(leftDepth == -2 || rightDepth == -2 || flag > 1 || flag < -1) return -2;else return (leftDepth > rightDepth ? leftDepth : rightDepth) + 1;}
}
[简单] 257. 二叉树的所有路径
原题链接
思路就是DFS深度优先遍历找到每一条路径,效率差异主要体现在对字符串拼接的处理上,使用StringBuilder会更高效一些。

class Solution {public List<String> binaryTreePaths(TreeNode root) {List<String> ans = new ArrayList<>();if(root == null) return ans;DFS(root, ans, "");return ans;}public void DFS(TreeNode p, List<String> ans, String string){StringBuilder sb = new StringBuilder(string);sb.append(p.val);if(p.left == null && p.right == null){ans.add(sb.toString());return;}sb.append("->");if(p.left != null)DFS(p.left, ans, sb.toString());if(p.right != null)DFS(p.right, ans, sb.toString());}
}
相关文章:

LeetCode——二叉树(Java)
二叉树 简介[简单] 144. 二叉树的前序遍历、94. 二叉树的中序遍历、145. 二叉树的后序遍历二叉树层序遍历[中等] 102. 二叉树的层序遍历[中等] 107. 二叉树的层序遍历 II[中等] 199. 二叉树的右视图[简单] 637. 二叉树的层平均值[中等] 429. N 叉树的层序遍历[中等] 515. 在每个…...
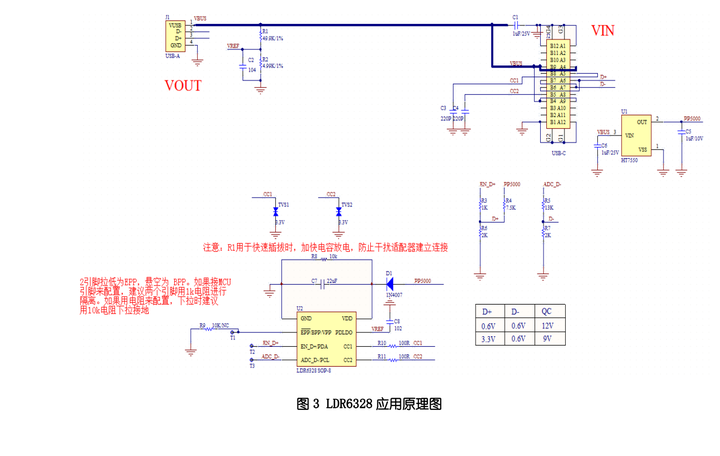
LDR6328芯片:智能家居时代的小家电充电革新者
在当今的智能家居时代,小家电的供电方式正变得越来越智能化和高效化。 利用PD(Power Delivery)芯片进行诱骗取电,为后端小家电提供稳定电压的技术,正逐渐成为行业的新宠。在这一领域,LDR6328芯片以其出色的…...

用node写后端环境运行时报错Port 3000 is already in use
解决方法:关闭之前运行的3000端口,操作如下 1.WindowR输入cmd确定,打开命令面板 2.查看本机端口详情 netstat -ano|findstr "3000" 3.清除3000端口 taskkill -pid 41640 -f 最后再重新npm start即可,这里要看你自己项目中package.joson的启动命令是什…...
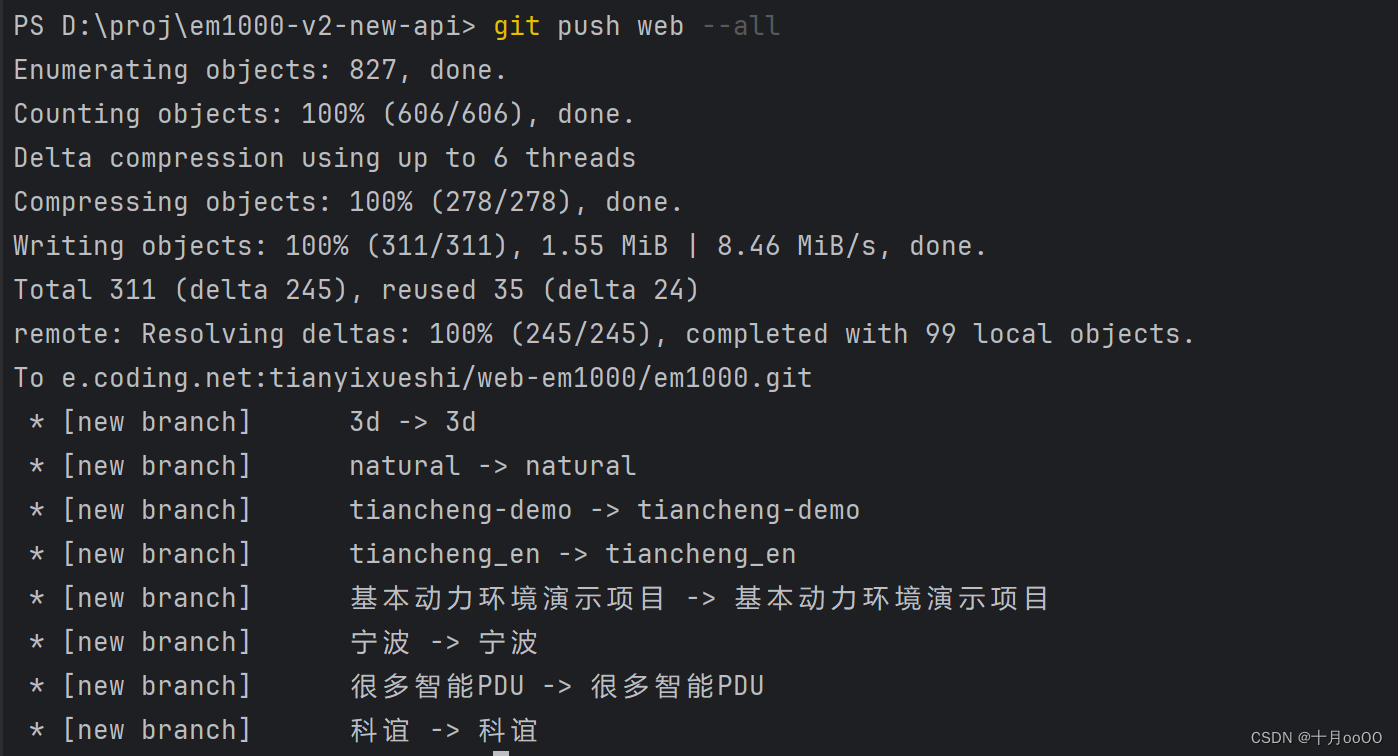
Git 如何上传本地的所有分支
Git 如何上传本地的所有分支 比如一个本地 git 仓库里定义了两个远程分支,一个名为 origin, 一个名为 web 现在本地有一些分支是 web 远程仓库没有的分支,如何将本地所有分支都推送到 web 这个远程仓库上呢 git push web --all...
【airtest】自动化入门教程(一)AirtestIDE
目录 一、下载与安装 1、下载 2、安装 3、打开软件 二、web自动化配置 1、配置chrome浏览器 2、窗口勾选selenium window 三、新建项目(web) 1、新建一个Airtest项目 2、初始化代码 3、打开一个网页 四、恢复默认布局 五、新建项目…...

ChatGPT支持下的PyTorch机器学习与深度学习技术应用
近年来,随着AlphaGo、无人驾驶汽车、医学影像智慧辅助诊疗、ImageNet竞赛等热点事件的发生,人工智能迎来了新一轮的发展浪潮。尤其是深度学习技术,在许多行业都取得了颠覆性的成果。另外,近年来,Pytorch深度学习框架受…...
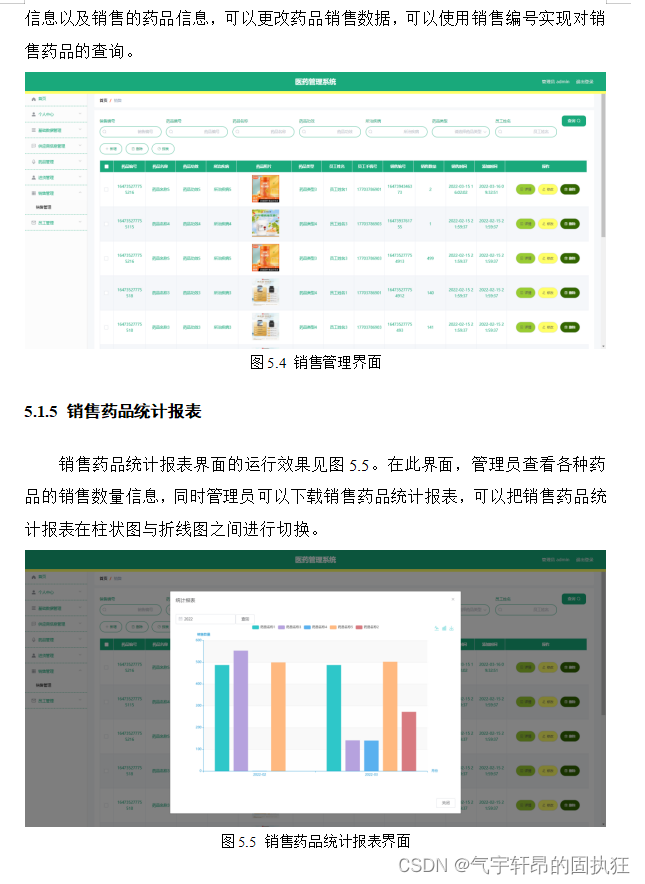
Springboot+vue的医药管理系统(有报告)。Javaee项目,springboot vue前后端分离项目。
演示视频: Springbootvue的医药管理系统(有报告)。Javaee项目,springboot vue前后端分离项目。 项目介绍: 采用M(model)V(view)C(controller)三层…...
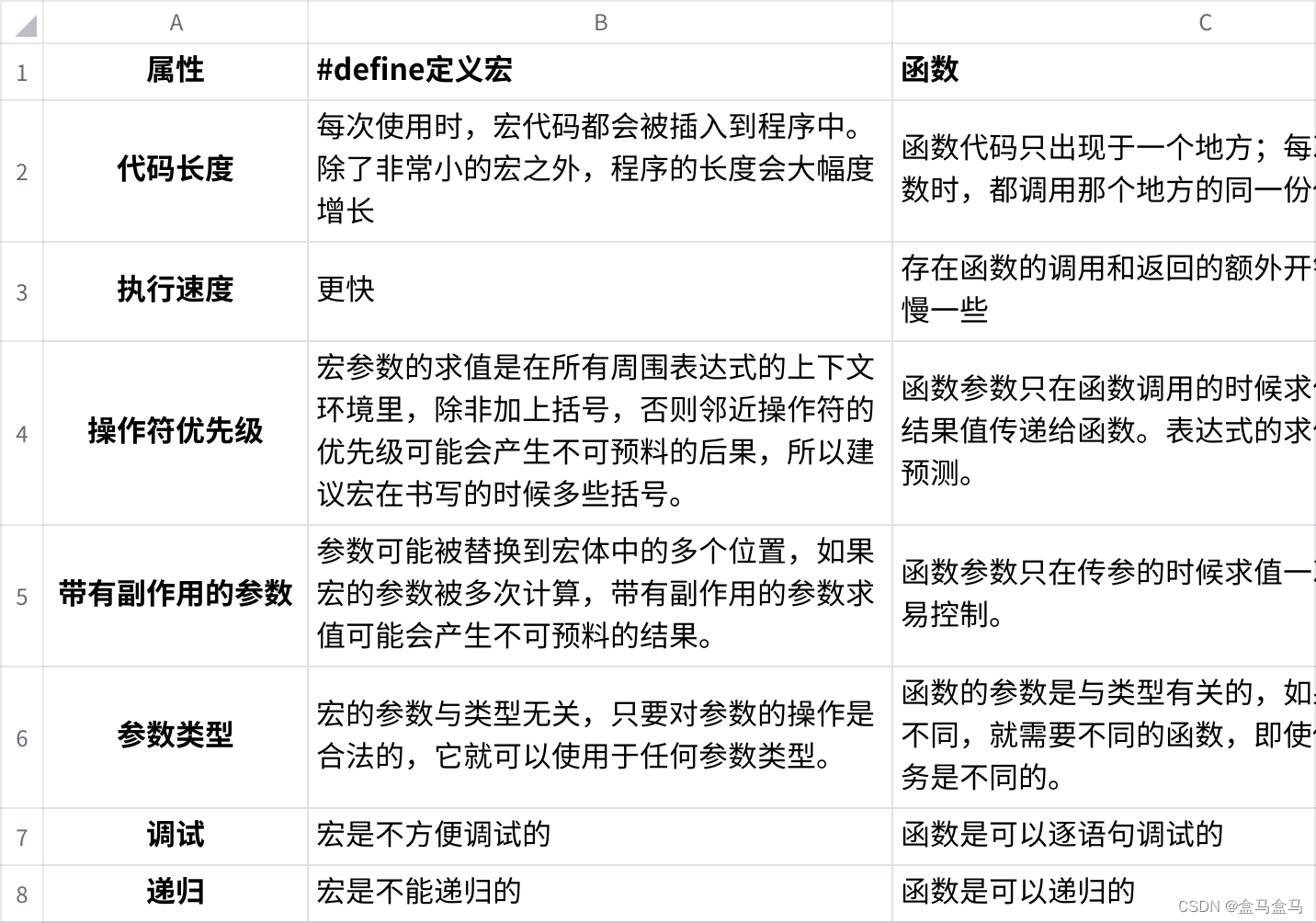
C语言:预处理
C语言:预处理 预定义符号#define定义常量定义宏宏与函数对比 #操作符##操作符条件编译头文件包含库文件包含本地文件包含嵌套文件包含 预定义符号 C语⾔设置了⼀些预定义符号,可以直接使⽤,预定义符号也是在预处理期间处理的。 __FILE__ //…...
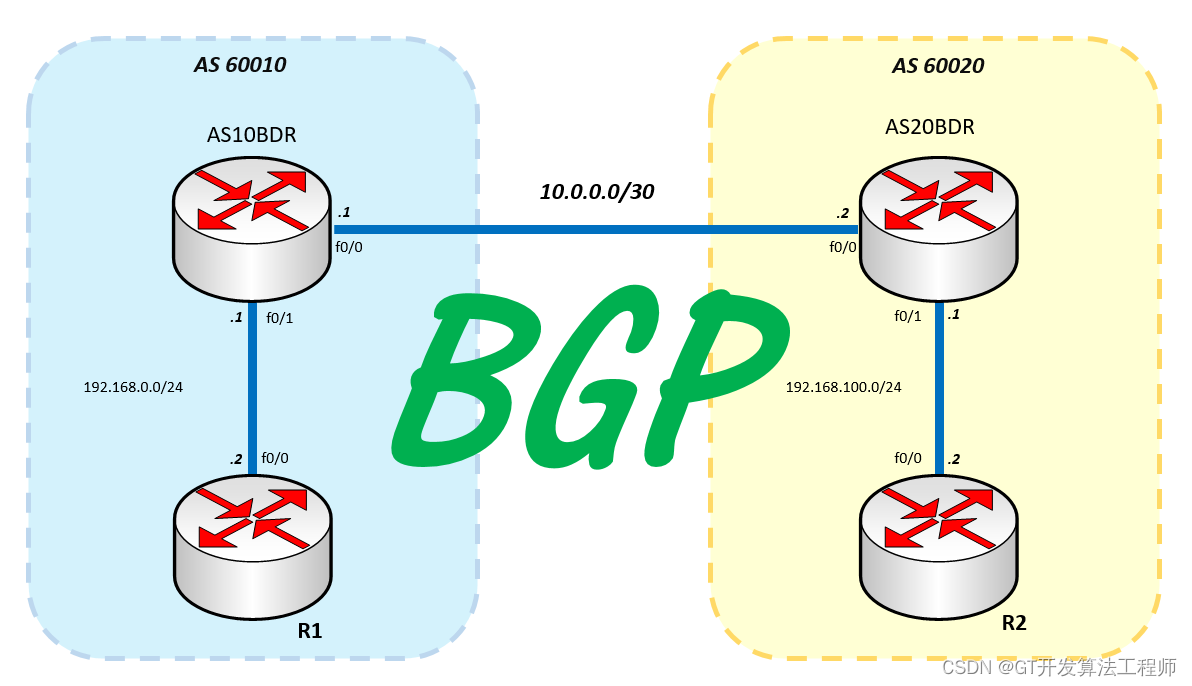
计算机网络:路由协议
路由协议简介 路由协议是计算机网络中不可或缺的一部分,它们负责确定数据包从源地址到目的地址的最佳路径。想象一下,如果你是一个数据包,路由协议就像是地图或导航工具,指导你如何到达目的地。 目录 路由协议简介 工作原理简化…...

经典动态规划题目leetcode322. 零钱兑换
题目链接:https://leetcode.cn/problems/coin-change/description/ 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合…...
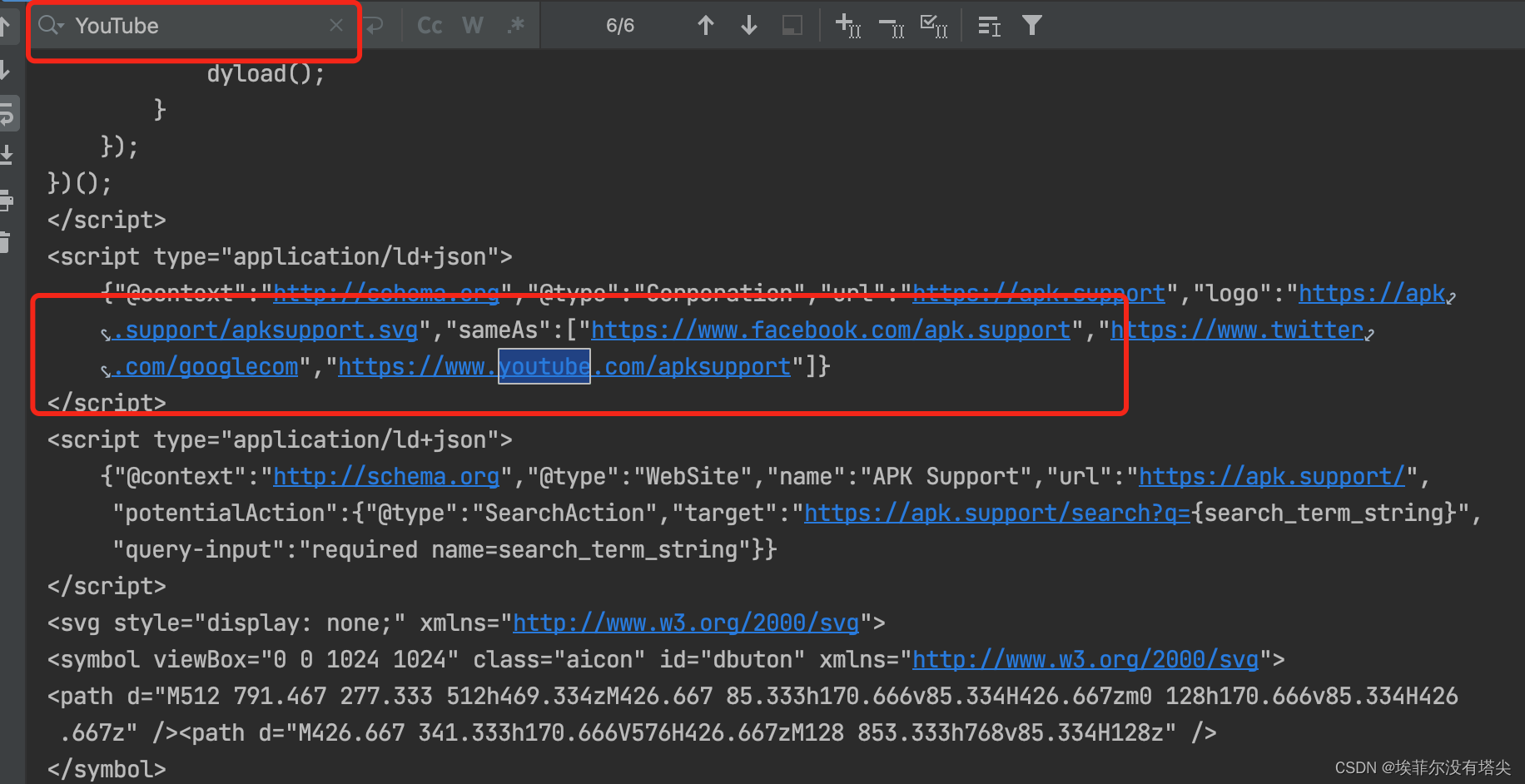
python 使用curl_cffi 绕过jax3指纹-Cloudflare 5s盾
现在越来越多的网站已经能够通过JA3或者其他指纹信息,来识别你是不是爬虫了。传统的方式比如换UA,加代理是没有任何意义了,所以这个时候我们就需要使用到curl_cffi 了。 1.TLS 指纹是啥? 在绝大多数的网站都已经使用了 HTTPS&am…...

Python3学习笔记39-passlib
passlib处理密码哈希的python包,支持很多哈希算法和工具 bcrypt 安装 pip install passlib[bcrypt] 会安装passlib包和bcrypt两个包 密码哈希与校验 from passlib.context import CryptContext# 创建CryptContext对象,指定加密算法 pwd_context CryptContext…...
Matlab 机器人工具箱 动力学
文章目录 R.dynR.fdynR.accelR.rneR.gravloadR.inertiaR.coriolisR.payload官网:Robotics Toolbox - Peter Corke R.dyn 查看动力学参数 mdl_puma560; p560.dyn;%查看puma560机械臂所有连杆的动力学参数 p560.dyn(2);%查看puma560机械臂第二连杆的动力学参数 p560.links(2)…...

Android ShellUtils手机管理器
1. Android ShellUtils手机管理器 Android Shell工具类,可用于检查系统root权限,并在shell或root用户下执行shell命令。如: checkRootPermission() 检查root权限 。execCommand(String[] commands, boolean isRoot, boolean isNeedResultMsg)…...

《梦幻西游》本人收集的34个单机版游戏,有详细的视频架设教程,值得收藏
梦幻西游这款游戏,很多人玩,喜欢研究的赶快下载吧。精心收集的34个版本。不容易啊。里面有详细的视频架设教程,可以外网呢。 《梦幻西游》本人收集的34个单机版游戏,有详细的视频架设教程,值得收藏 下载地址࿱…...

吴恩达机器学习全课程笔记第六篇
目录 前言 P96-P100 使用多个决策树 随机森林算法 XGBoost 什么时候使用决策树 P101-P107 聚类 K-means 初始化K-means 选择聚类的个数 P108-P113 异常检测算法 开发和评估异常检测系统 异常检测vs监督学习 选择要使用的特征 前言 这是吴恩达机器学习笔记的第…...
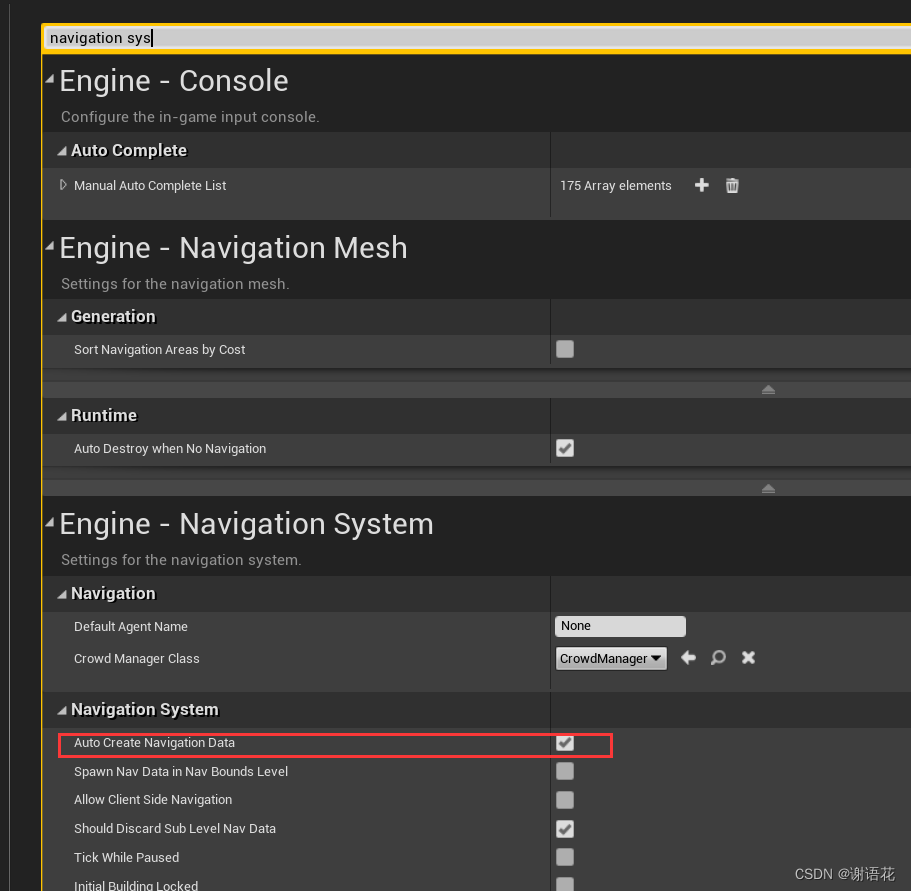
ue4.27 发现 getRandomReachedLocation 返回 false
把这个玩意儿删掉,重启工程,即可 如果还不行 保证运动物体在 volum 内部,也就是绿色范围内确保 project setting 里面的 navigation system 中 auto create navigation data 是打开的(看到过博客说关掉,不知道为啥) 如果还不行&…...
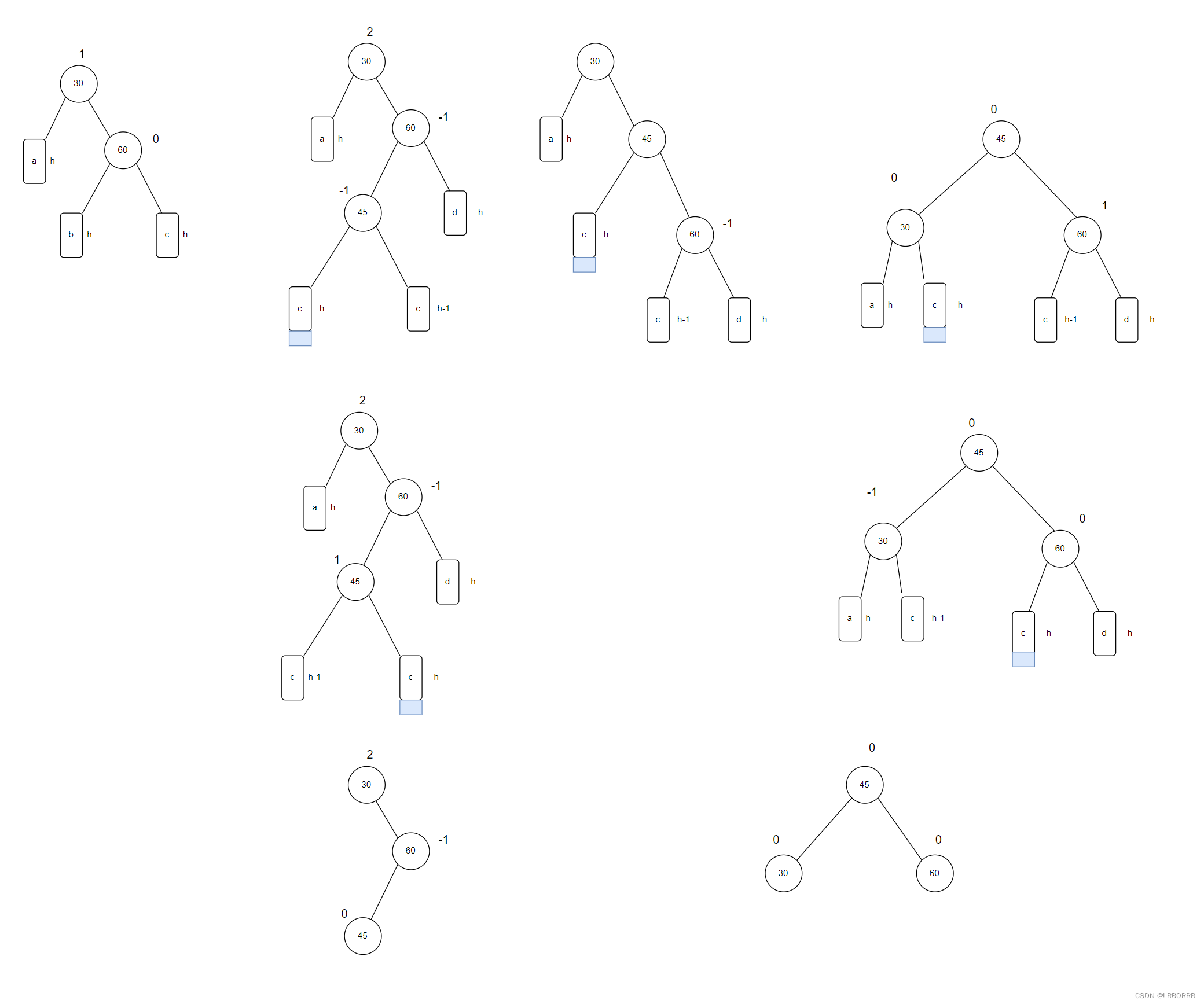
【C++ AVL树】
文章目录 AVL树AVL树的概念AVL树节点的定义AVL树的插入AVL树的旋转右单旋左单旋左右双旋右左双旋 代码实现 总结 AVL树 AVL树的概念 二叉搜索树在顺序有序或接近有序的情况下,而插入搜索树将退化为单叉树,此时查找的时间复杂度为O(n),效率低…...

记录一次架构优化处理性能从3千->3万
0.背景 优化Kafka消费入Es,适配600台设备上报数据,吞吐量到达2万每秒 1.环境配置 2.压测工具 3.未优化之前的消费逻辑 4.优化之后的消费流程 5.多线程多ESclient 6.修改ES配置,增加kafka分区,增加线程,提升吞吐量 7.…...

c++二进制位运算使用方法
文章主要内容: C 中的位运算符主要用于对整数类型的数据进行位操作,包括按位与(&)、按位或(|)、按位异或(^)、取反(~)、左移(<<&#…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
