平衡二叉树,二叉树的路径,左叶子之和
第六章 二叉树part04
今日内容:
- 110.平衡二叉树
- 257. 二叉树的所有路径
- 404.左叶子之和
110.平衡二叉树 (优先掌握递归)
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
返回 false 。
递归法:
递归三步曲分析:
- 明确递归函数的参数和返回值
参数:当前传入节点。 返回值:以当前传入节点为根节点的树的高度。那么如何标记左右子树是否差值大于1呢?
如果当前传入节点为根节点的二叉树已经不是二叉平衡树了,还返回高度的话就没有意义了。
所以如果已经不是二叉平衡树了,可以返回-1 来标记已经不符合平衡树的规则了。
- 明确终止条件
递归的过程中依然是遇到空节点了为终止,返回0,表示当前节点为根节点的树高度为0
- 明确单层递归的逻辑
如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢?当然是其左子树高度和其右子树高度的差值。
分别求出其左右子树的高度,然后如果差值小于等于1,则返回当前二叉树的高度,否则返回-1,表示已经不是二叉平衡树了。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isBalanced(TreeNode root) {
return getHeight(root)!=-1;
}
public int getHeight(TreeNode root)
{
if(root==null) return 0;
int leftHeight = getHeight(root.left);
if(leftHeight==-1)return -1;
int rightHeight = getHeight(root.right);
if(rightHeight==-1)return -1;
if(Math.abs(leftHeight-rightHeight)>1) return -1;
else return Math.max(leftHeight,rightHeight)+1;
}
}
257. 二叉树的所有路径
给定一个二叉树,返回所有从根节点到叶子节点的路径
思路
这道题目要求从根节点到叶子的路径,所以需要前序遍历,这样才方便让父节点指向孩子节点,找到对应的路径。
在这道题目中将第一次涉及到回溯,因为我们要把路径记录下来,需要回溯来回退一个路径再进入另一个路径。
递归
- 递归函数参数以及返回值
要传入根节点,记录每一条路径的path,和存放结果集的result,这里递归不需要返回值。
- 确定递归终止条件
本题要找到叶子节点,就开始结束的处理逻辑了(把路径放进result里)。
那么什么时候算是找到了叶子节点? 是当 cur不为空,其左右孩子都为空的时候,就找到叶子节点。
- 确定单层递归逻辑
因为是前序遍历,需要先处理中间节点,中间节点就是我们要记录路径上的节点,先放进path中。
然后是递归和回溯的过程,上面说过没有判断cur是否为空,那么在这里递归的时候,如果为空就不进行下一层递归了。
回溯和递归是一一对应的,有一个递归,就要有一个回溯。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String> result = new ArrayList<>();
List<Integer> paths = new ArrayList<>();
if(root==null) return result;
travesal(root,result,paths);
return result;
}
public void travesal(TreeNode root,List<String> result,List<Integer> paths)
{
paths.add(root.val);
if(root.left==null&&root.right==null)
{
StringBuilder sb = new StringBuilder();
for(int i=0;i<paths.size()-1;i++) sb.append(paths.get(i)).append("->");
sb.append(paths.get(paths.size()-1));
String path = sb.toString();
result.add(path);
return;
}
if(root.left!=null)
{
travesal(root.left,result,paths);
paths.remove(paths.size()-1);
}
if(root.right!=null)
{
travesal(root.right,result,paths);
paths.remove(paths.size()-1);
}
}
}
404.左叶子之和 (优先掌握递归)
计算给定二叉树的所有左叶子之和。
首先要注意是判断左叶子,不是二叉树左侧节点,所以不要上来想着层序遍历。
节点A的左孩子不为空,且左孩子的左右孩子都为空(说明是叶子节点),那么A节点的左孩子为左叶子节点
判断当前节点是不是左叶子是无法判断的,必须要通过节点的父节点来判断其左孩子是不是左叶子。
递归法
递归的遍历顺序为后序遍历(左右中),是因为要通过递归函数的返回值来累加求取左叶子数值之和。
递归三部曲:
- 确定递归函数的参数和返回值
判断一个树的左叶子节点之和,那么一定要传入树的根节点,递归函数的返回值为数值之和,所以为int使用题目中给出的函数就可以了。
- 确定终止条件
如果遍历到空节点,那么左叶子值一定是0
只有当前遍历的节点是父节点,才能判断其子节点是不是左叶子。 所以如果当前遍历的节点是叶子节点,那其左叶子也必定是0。
- 确定单层递归的逻辑
当遇到左叶子节点的时候,记录数值,然后通过递归求取左子树左叶子之和,和 右子树左叶子之和,相加便是整个树的左叶子之和。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
if(root==null) return 0;
if(root.left==null&&root.right==null) return 0;
int leftSum = sumOfLeftLeaves(root.left);
if(root.left!=null&&root.left.left==null&&root.left.right==null)
leftSum = root.left.val;
int rightSum = sumOfLeftLeaves(root.right);
int sum = leftSum+rightSum;
return sum;
}
}
相关文章:

平衡二叉树,二叉树的路径,左叶子之和
第六章 二叉树part04 今日内容: 110.平衡二叉树 257. 二叉树的所有路径 404.左叶子之和 110.平衡二叉树 (优先掌握递归) 给定一个二叉树,判断它是否是高度平衡的二叉树。 本题中,一棵高度平衡二叉树定义为&am…...

Sodinokibi勒索病毒最新变种,解密工具更新到2.0版本
Sodinokibi勒索病毒 Sodinokibi勒索病毒又称REvil,自从2019年6月1日,GandCrab勒索病毒运营团伙宣布停止运营之后,Sodinokibi勒索病毒马上接管了GandCrab的大部分传播渠道,同时它也被称为是GandCrab勒索病毒的“接班人”ÿ…...

css 鼠标移入放大的效果
效果 HTML <div class"img-wrap"><img class"img-item" src"../assets/1.png" alt"" srcset""></div> CSS <style lang"less" scoped> .img-wrap {/* 超出隐藏 */overflow: hidden;.img-…...

Transformer模型分布式并行通信量浅析
1.数据并行DP(朴素数据并行,Zero数据并行之后补充) O ( h 2 ∗ l ) O(h^2*l) O(h2∗l) 每台机器做完自己的梯度后需要做一次All reduce操作来累积梯度,故一个batch计算发送的数据量为每层梯度大小 h 2 h^2 h2乘以层数 l l l 优点…...

PMP考试之20240304
1.一家食品公司正在使用预测型方法开发一种新产品,该产品目前正处于测试阶段。鉴于测试反馈的性质,项目经理决定使用迭代方法。在其中一个迭代结束时,颁布了与该产品有关的新法规。项目经理接下来应该做什么? A.就项目的范围提出…...

智慧城市中的公共服务创新:让城市生活更便捷
目录 一、引言 二、智慧城市公共服务创新的实践 1、智慧交通系统 2、智慧医疗服务 3、智慧教育系统 4、智慧能源管理 三、智慧城市公共服务创新的挑战 四、智慧城市公共服务创新的前景 五、结论 一、引言 随着信息技术的迅猛发展,智慧城市已成为现代城市发…...
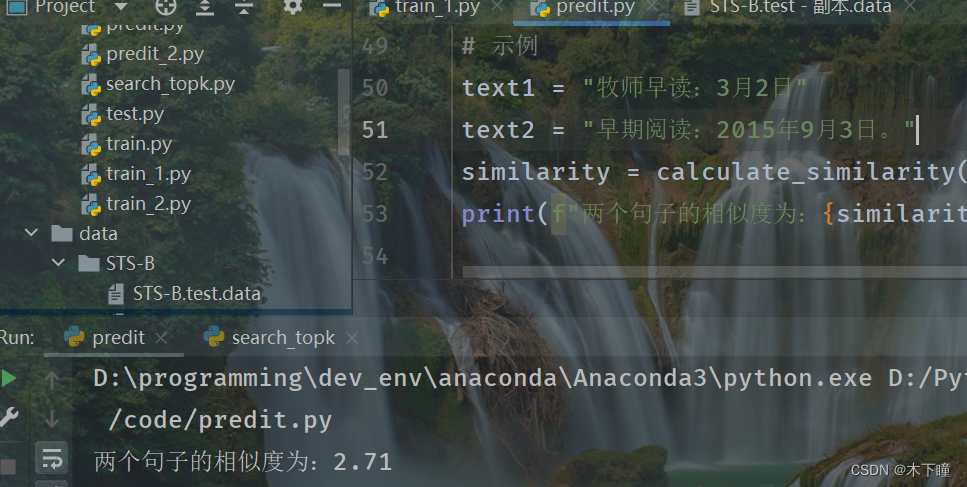
bert 相似度任务训练完整版
任务 之前写了一个相似度任务的版本:bert 相似度任务训练简单版本,faiss 寻找相似 topk-CSDN博客 相似度用的是 0,1,相当于分类任务,现在我们相似度有评分,不再是 0,1 了,分数为 0-5,数字越大…...

Ribbon实现Cloud负载均衡
安装Zookeeper要先安装JDK环境 解压 tar -zxvf /usr/local/develop/jdk-8u191-linux-x64.tar.gz -C /usr/local/develop 配置JAVA_HOME vim /etc/profile export JAVA_HOME/usr/local/develop/jdk1.8.0_191 export PATH$JAVA_HOME/bin:$PATH export CLASSPATH.:$JAVA_HOM…...
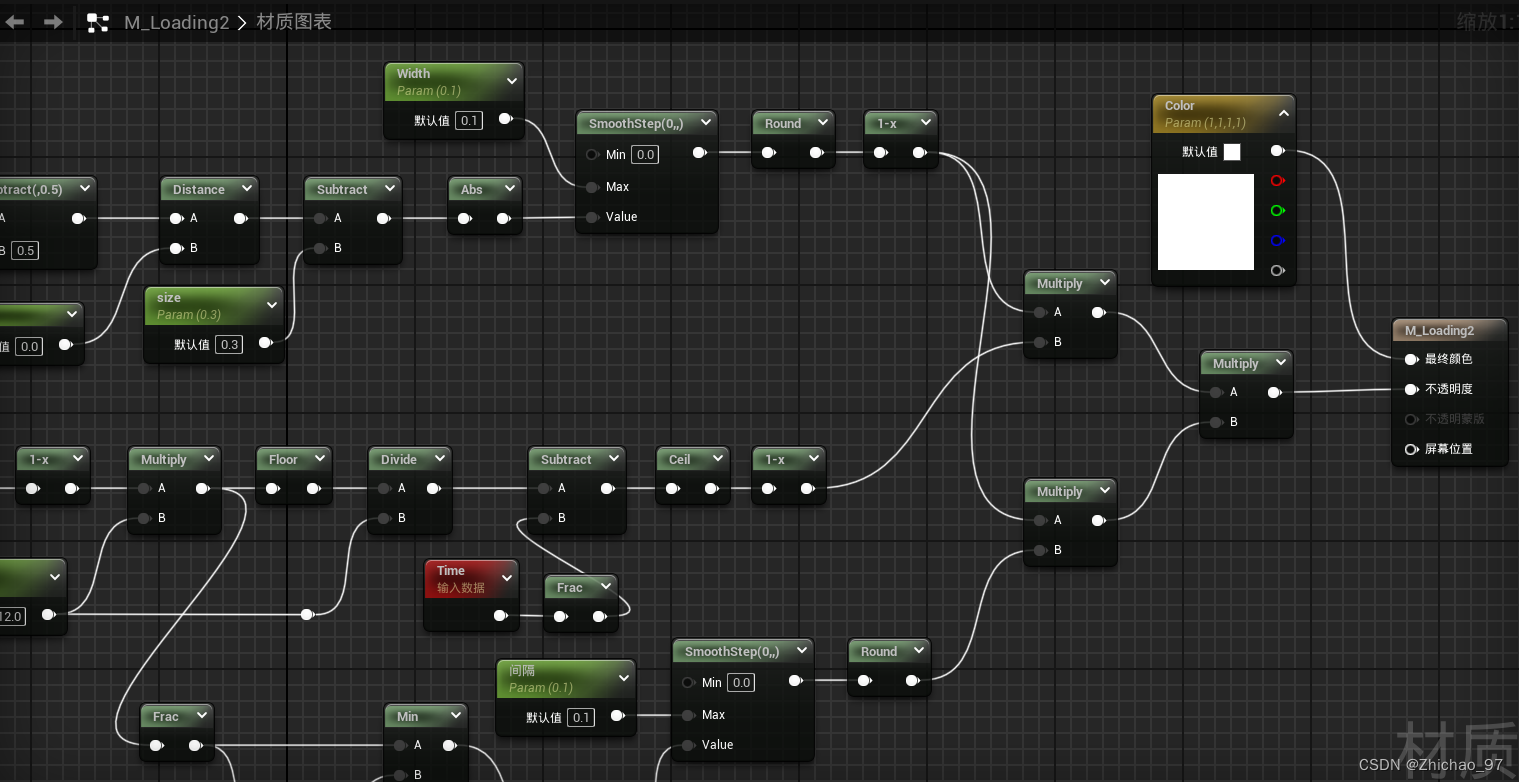
【UE 材质】制作加载图案(2)
在上一篇(【UE 材质】制作加载图案)基础上继续实现如下效果的加载图案 效果 步骤 1. 复制一份上一篇制作的材质并打开 2. 添加“Floor”节点向下取整 除相同的平铺数 此时的效果如下 删除如下节点 通过“Ceil”向上取整,参数“Tiling”默认…...

为啥要用C艹不用C?
在很多时候,有人会有这样的疑问 ——为什么要用C?C相对于C优势是什么? 最近两年一直在做Linux应用,能明显的感受到C带来到帮助以及快感 之前,我在文章里面提到环形队列 C语言,环形队列 环形队列到底是怎么回…...
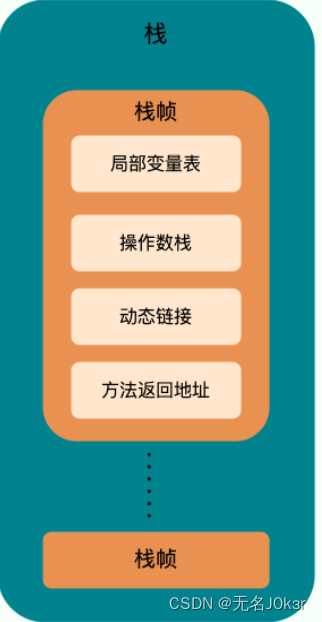
Java:JVM基础
文章目录 参考JVM内存区域程序计数器虚拟机栈本地方法栈堆方法区符号引用与直接引用运行时常量池字符串常量池直接内存 参考 JavaGuide JVM内存区域 程序计数器 程序计数器是一块较小的内存空间,可以看做是当前线程所执行的字节码的行号指示器,各线程…...

JavaSec 基础之五大不安全组件
文章目录 不安全组件(框架)-Shiro&FastJson&Jackson&XStream&Log4jLog4jShiroJacksonFastJsonXStream 不安全组件(框架)-Shiro&FastJson&Jackson&XStream&Log4j Log4j Apache的一个开源项目,是一个基于Java的日志记录框架。 历史…...

python类的属性、方法、静态方法、静态方法类内部的调用、直接调用与实例化调用
设计者:ISDF工软未来 版本:v1.0 日期:2024/3/4 class Restaurant:餐馆类def __init__(self,restaurant_name,cuisine_type):#类的属性self.restaurant_name restaurant_nameself.cuisine_type cuisine_type# self.stregth_level 0def desc…...

haproxy集成国密ssl功能[下]
上接[haproxy集成国密ssl功能上 4. 源码修改解析 以下修改基本围绕haproxy的ssl_sock.c进行修改来展开的,为了将整个实现逻辑能够说明清楚,下述内容有部分可能就是直接摘抄haproxy的原有代码没有做任何修改,而大部分增加或者修改的内容则进行了特别的说明。 4.1 为bind指令…...
C++自学精简实践教程
一、介绍 1.1 教程特点 一篇文章从入门到就业有图有真相,有测试用例,有作业;提供框架代码,作业只需要代码填空规范开发习惯,培养设计能力 1.2 参考书 唯一参考书《C Primer 第5版》参考书下载: 蓝奏云…...

每日一题——LeetCode1572.矩阵对角线元素的和
方法一 遍历矩阵 如果矩阵中某个位置(x,y)处于对角线上,那么这个位置必定满足: xy 或 xy len-1 (len为矩阵长度) var diagonalSum function(mat) {let len mat.length;let sum 0;for (let i 0; i …...
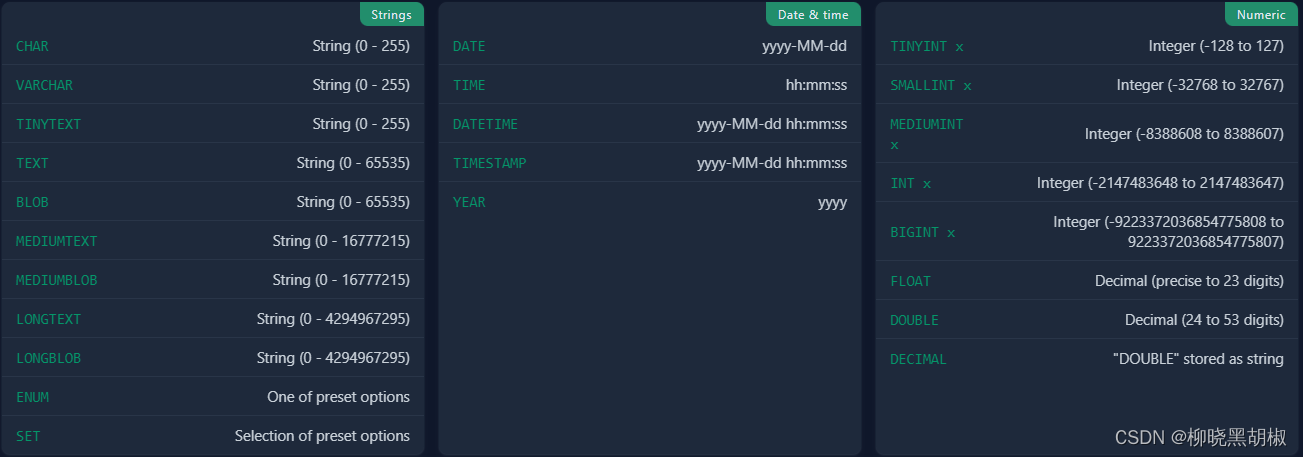
mysql 常用命令练习
管理表格从表中查询数据从多个表查询修改数据sql变量类型 管理表格 创建一个包含三列的新表 CREATE TABLE products (id INT,name VARCHAR(255) NOT NULL,price INT DEFAULT 0,PRIMARY KEY(id) // 自增 ); 从数据库中删除表 DROP TABLE product; 向表中添加新列 ALTER TAB…...

QT6 libModbus 用于ModbusTcp客户端读写服务端
虽然在以前的文章中多次描述过,那么本文使用开源库libModbus,可得到更好的性能,也可移植到各种平台。 性能:读1次和写1次约各用时2ms。 分别创建了读和写各1个连接指针,用于读100个寄存器和写100个寄存器,读写分离。 客户端&am…...
Tensor使用教程)
飞桨(PaddlePaddle)Tensor使用教程
文章目录 飞桨(PaddlePaddle)Tensor使用教程1. 安装飞桨2. 创建Tensor3. Tensor的基本属性4. Tensor的操作5. Tensor的广播机制6. Tensor与Numpy数组的转换7. 结论 飞桨(PaddlePaddle)Tensor使用教程 1. 安装飞桨 首先ÿ…...
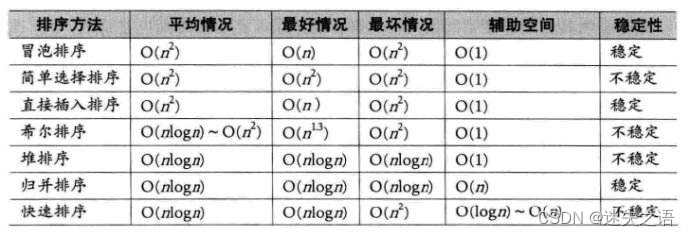
数据结构c版(3)——排序算法
本章我们来学习一下数据结构的排序算法! 目录 1.排序的概念及其运用 1.1排序的概念 1.2 常见的排序算法 2.常见排序算法的实现 2.1 插入排序 2.1.1基本思想: 2.1.2直接插入排序: 2.1.3 希尔排序( 缩小增量排序 ) 2.2 选择排序 2.2…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...
如何做好一份技术文档?从规划到实践的完整指南
如何做好一份技术文档?从规划到实践的完整指南 🌟 嗨,我是IRpickstars! 🌌 总有一行代码,能点亮万千星辰。 🔍 在技术的宇宙中,我愿做永不停歇的探索者。 ✨ 用代码丈量世界&…...

【多线程初阶】单例模式 指令重排序问题
文章目录 1.单例模式1)饿汉模式2)懒汉模式①.单线程版本②.多线程版本 2.分析单例模式里的线程安全问题1)饿汉模式2)懒汉模式懒汉模式是如何出现线程安全问题的 3.解决问题进一步优化加锁导致的执行效率优化预防内存可见性问题 4.解决指令重排序问题 1.单例模式 单例模式确保某…...
——Oracle for Linux物理DG环境搭建(2))
Oracle实用参考(13)——Oracle for Linux物理DG环境搭建(2)
13.2. Oracle for Linux物理DG环境搭建 Oracle 数据库的DataGuard技术方案,业界也称为DG,其在数据库高可用、容灾及负载分离等方面,都有着非常广泛的应用,对此,前面相关章节已做过较为详尽的讲解,此处不再赘述。 需要说明的是, DG方案又分为物理DG和逻辑DG,两者的搭建…...
