概率论 1.3 古典概型与几何概型

1.3.1 排列与组合
排列
从n个不同元素任取r(r<=n)个元素排成一列(考虑元素出现的先后次序),称此为一个排列,此种排列的总数为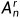 =n(n-1)....(n-r+1)=n!/(n-r)!,若r=n,则称为全排列,
=n(n-1)....(n-r+1)=n!/(n-r)!,若r=n,则称为全排列,
2.重复排列
从n个不同元素中每次取出一个,放回后再取出;下一个,如此连续取,次所得的排列称为重复排列,此种重复排列数共有n个,这里, 允许大于么
3.组合
从n个不同元素中任取r(r<几)个元素并成一组(不考虑元素出现的先后次序),称为一个组合,此种组合的总数为
Ch
n (n
- 1)... (n r+1)
r!
nl
Fr! (n = r)!
易知
A, =Cr!, C, =C
排列组合公式在古典概型的概率计算中经常使用。
1.3.2 古典概型
具有以下两个特点的试验称为古典概型:
(1)有限性:试验的样本空间只含有限个样本点;
(2) 等可能性:试验中每个基本事件发生的可能性相同
对于古典概型,若样本空间中共有n个样本点,事件A 包含人个样本点,则事件
A 的概率为
事件4 中所包含样本点的个数
P(A)
2中所有样本点的个数
容易验证,由上式确定的概率满足公理化定义
【例 1.77(随机取数问题)从1,2,…,10共10个数字中任取一个,取后放回,
先后取出 7个数字,试求下列各事件的概率:
(1) A
=“7 个数字全不相同”;
(2) B
一“不含10与 1”;
(3)C=“10恰好出现两次”。
解随机试验的样本空问共含有10? 个不同的样本点,则
(3)对于事件C,出现两次 10可以是7次中的任意两次,故有C号种选择,其他5
次中,每次只能取剩下9个数字中的任何一个,故
C3 • 9
p(C)
0.124003.
107
例 1.8】(摸球问题)袋中有a 个白球,6个红球,k个人依次在袋中取一个球,
考虑下列两种取球方式,求第i(i=1,2,
,k)个人取到白球的概率.(1)作放回
抽样(即前一人取一个球观察颜色后放回袋中,后一个人再取一球),(2,作不放回抽
样(即前一人取一个球观察颜色后不放回袋中,后
-个人再取一球)
解记B=“第ii=1,2,
,k)个人取到白球”
1)放回抽样的情况.
第1个人取到白球的概率为-
2+6•因为是放回抽样,所以第2人,第3人,
第k人取到白球的概率均为
a大6,
P(B)=
a th
(2)不放回抽样的情况.
<个人各取一球,每种取法是一个基本事件,k 个人各取一球共有(a+6(a+6
-1∞[6a+6=(一11=A4,种取法.
当事件 B 发生时,第之人取的应是白球,它可以是a 个白球中的任一个,有a种
取法,其余被取的 k一1个球可以是其余a十6一1个球中的任意k一1个,共有(a+6
=16a+6=②∞16a+6=①=[¢=①+1J>=A千6-1种取法,所以
P(B)
a A"-b-i
A +6
a(a+6-①(a+6=1=1∞(a+6-1
(a +6(a+6=1∞€(a+6一k千17
- (k -1) +1
士6
值得注意的是,P(B)与之无关,即k 个人取球,尽管取球的先后次序不同,每个
人取到白球的概率是一样的,大家机会均等;放回抽样与不放回抽样取到白球的概率
也是一样的
类似的问题如购买彩票等,无论先买后买,中奖的概率是一样的.
【例1.9】(分房问题)
有几个人,每个人都以同样的概率被分配在 N(n≤N)间
房中的每一问中,试求下列各事件的概率:
(① A
一“某指定九间房中各有一人”
(2)B一“恰有几间房,其中各有一人”;
到达,所以由等可能性知这是一个几何概型问题,
样本空间2=1(z,3):0≤z,3≤60)
事件 A=“甲乙能会面”={(z,>)E2:1z一31≤20),因此
pPeA)一 附面餐
< 602
- 402
602
【例 1.11】<蒲丰投针问题)
平面上面有间隔为d (d二0的等距平行线,向平
面任意投掷一枚长为((L<d)的针,求针与任一平行线相交的概率.
解以,表示针的中点与最近一条平行线的距离,又以9表示针与直线间的交
角,如图1.2 所示.易知样本空间 2满足
0≤¢
Fd
0
<0<%.
2
由这两式可以确定平面上的一个矩化口,口的面积y”
A二“针与平行线相交” 发生当且仅当0≤五≤元
因此
7
sinode
2
A 的面积
P(A)
一2的面积
2l
di
du
2
+47 (11477-15,5138)
-sing
o
图 1.2蒲丰投针问题
蒲丰投针试验的应用及意义:根据频率的稳定性,当投针试验次数n很大时,测
出针与平行线相交的次数m,则频率值〞
“即可作为PCA)的近似值代人上式,那么
m一dr
n
2nl
dm
利用上式可以计算圆周率元 的近似值.
【例1.12】 随机向边长为1的正方形内投点,试求点投在正方形的一条对角线
上的概率,如图1.3所示.
解样本空间 2=1(z,):0二z,y<1),事件 A=
“点投在正方形的对角线上”={(z,»):2三〉),因此
对角线的面积
O
P(A)
=
=0.
中方形的面积
1
说明:根据前面概率的性质 1,我们知道不可能事件
的概率为 0.本例表明,概率为。的事件未必是不可能事
件,可能发生.类似地,概率为1的事件也未必是必然

相关文章:

概率论 1.3 古典概型与几何概型
1.3.1 排列与组合排列从n个不同元素任取r(r<n)个元素排成一列(考虑元素出现的先后次序),称此为一个排列,此种排列的总数为n(n-1)....(n-r1)n!/(n-r)!,若rn,则称为全排列,2.重复排列从n个不同元素中每次取出一个,放回…...

HTML DOM
通过 HTML DOM,可访问 JavaScript HTML 文档的所有元素。HTML DOM (文档对象模型)当网页被加载时,浏览器会创建页面的文档对象模型(Document Object Model)。HTML DOM 定义了用于 HTML 的一系列标准的对象,以及访问和处…...
Vue组件-$refs、$nextTick和name属性的使用
Vue组件-$refs和$nextTick使用一、获取DOM二、$refs获取组件对象三、$nextTick异步更新DOM四、组件name属性的使用一、获取DOM 通过id或ref属性获取原生DOM 在mounted生命周期 – 2种方式获取原生DOM标签 目标标签 – 添加id / ref恰当时机, 通过id / 通过ref属性 获取目标标签…...

【Spark】Spark的DataFrame向Impala写入数据异常及源码解析
背景 事情是这样的,当前业务有一个场景: 从业务库的Mysql抽取数据到Hive 由于运行环境的网络限制,当前选择的方案: 使用spark抽取业务库的数据表,然后利用impala jdbc数据灌输到hive。(没有spark on hive 的条件&…...

学习笔记-架构的演进之限流-3月day03
文章目录前言限流的目标流量统计指标限流设计模式流量计数器模式滑动时间窗模式漏桶模式令牌桶模式分布式限流总结附前言 任何一个系统的运算、存储、网络资源都不是无限的,当系统资源不足以支撑外部超过预期的突发流量时,就应该要有取舍,建…...
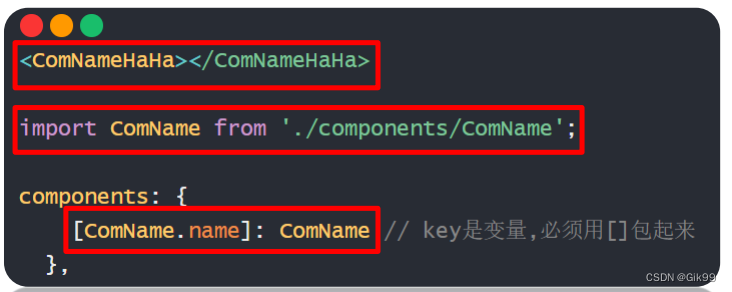
动态规划 背包问题
动态规划 背包问题 问题描述: 有一个背包,总容量为12。有6件物品,每件物品的重量和价值不同,求在背包总容量12的前提下,装进物品的最大价值以及装进物品的编号 单个物品重量和价值: 为方便进行思考&#…...
—— 内存模型和名称空间)
C++ Primer Plus 学习笔记(四)—— 内存模型和名称空间
1 单独编译 C允许将组件函数放在独立的文件即头文件中,头文件中可以包含以下内容: 函数原型;使用#define或const定义的符号常量;结构声明;类声明;模板声明;内联函数。 注意,在包含…...
详解基于 Celestia、Eclipse 构建的首个Layer3 链 Nautilus Chain
以流支付为主要概念的Zebec生态,正在推动流支付这种新兴的支付方式向更远的方向发展,该生态最初以Zebec Protocol的形态发展,并从初期的Solana进一步拓展至BNB Chian以及Near上。与此同时,Zebec生态也在积极的寻求从协议形态向公链…...

列表与数组的转化
目录用np.array(a)将列表转换为数组列表转数组的特殊情况(一)列表转数组的特殊情况(二)针对子元素个数不一致的解决办法用a.tolist()函数将数组转化为列表在python的学习中,经常会用到数组与列表的相互转化,本文主要介绍下关于数组与列表转化的问题。用n…...
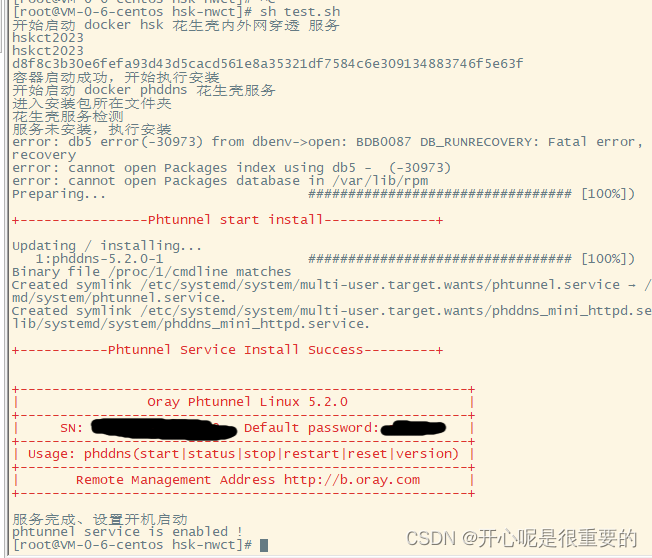
docker 运行花生壳实现内外网穿透
环境:centos 7 ,64位 1、创建一个指定的文件夹作为安装示例所用,该示例文件夹为“hsk-nwct”。“hsk-nwct”内创建“app”文件夹作为docker容器挂载出来的文件。 2、在“app”内下载花生壳linux安装包,下载花生壳应用:花生壳客户…...
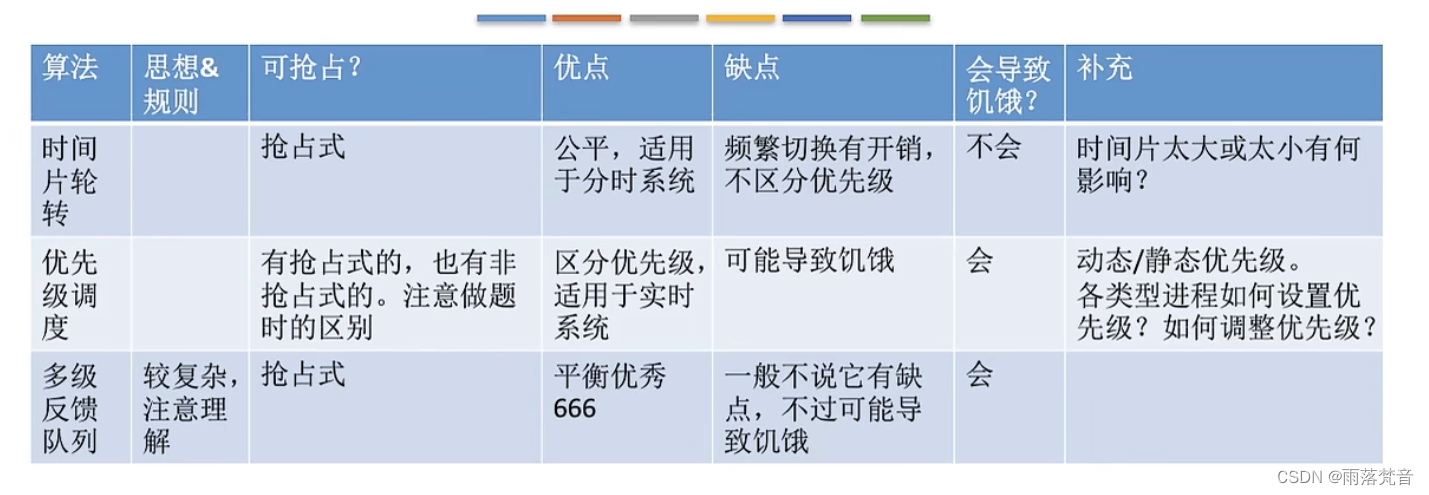
操作系统——16.时间片轮转、优先级、多级反馈队列算法
这篇文章我们来看一下进程调度算法中的时间片轮转、优先级、多级反馈队列算法 目录 1.概述 2.时间片轮转调度算法(RR,Round-Robin) 3.优先级调度算法 4.多级反馈队列调度算法 5.分析对比 1.概述 首先,我们来看一下这篇文章…...

Python3.8.8-Django3.2-Redis-连接池-数据类型-字符串-list-hashmap-命令行操作
文章目录1.认识Redis1.1.优点1.2.缺点2.在Django中Redis的连接3.Redis的基础用法3.1.hashmap结构3.2.list结构4.命令行查看数据库5.作者答疑1.认识Redis Remote DIctionary Server(Redis) 是一个key-value 存储系统,是跨平台的非关系型数据库。是一个开源的使用 AN…...

Android kotlin 系列讲解(进阶篇)高级项目架构模式 - MVVM
<<返回总目录 1、MVVM是什么 MVVM是Model-View-ViewModel的缩写,是一种高级项目架构模式。 MVVM架构可以将程序结构主要分成三个部分: Model:数据模型部分,包括从服务端获取的json数据或者从本地获取的数据等等View&…...

8. 查找
1 题目描述 查找成绩10开启时间2021年09月24日 星期五 18:00折扣0.8折扣时间2021年11月15日 星期一 00:00允许迟交否关闭时间2021年11月23日 星期二 00:00 输入 n(n ≤ 10^6)个不超过 10^9的单调不减的(就是后面的数字不小于前面的数字)非负整数 &#…...

二分查找算法
感谢“五点七边”工作室的算法讲解,详细内容可以参考视频讲解 二分查找为什么总是写错?_哔哩哔哩_bilibili 此处仅是个人学习总结 以target等于5为例,输入: 1 2 3 5 5 5 8 9 1. 找到第一个 > target 的元素 判断条件 < target&am…...
之远程服务器)
Git(3)之远程服务器
Git基础之远程服务器 Author:onceday date:2023年3月5日 满满长路有人对你微笑过嘛… windows安装可参考文章:git简易配置_onceday_CSDN博客 參考文档: 《progit2.pdf》,Progit2 Github。《git-book.pdf》 文章目…...
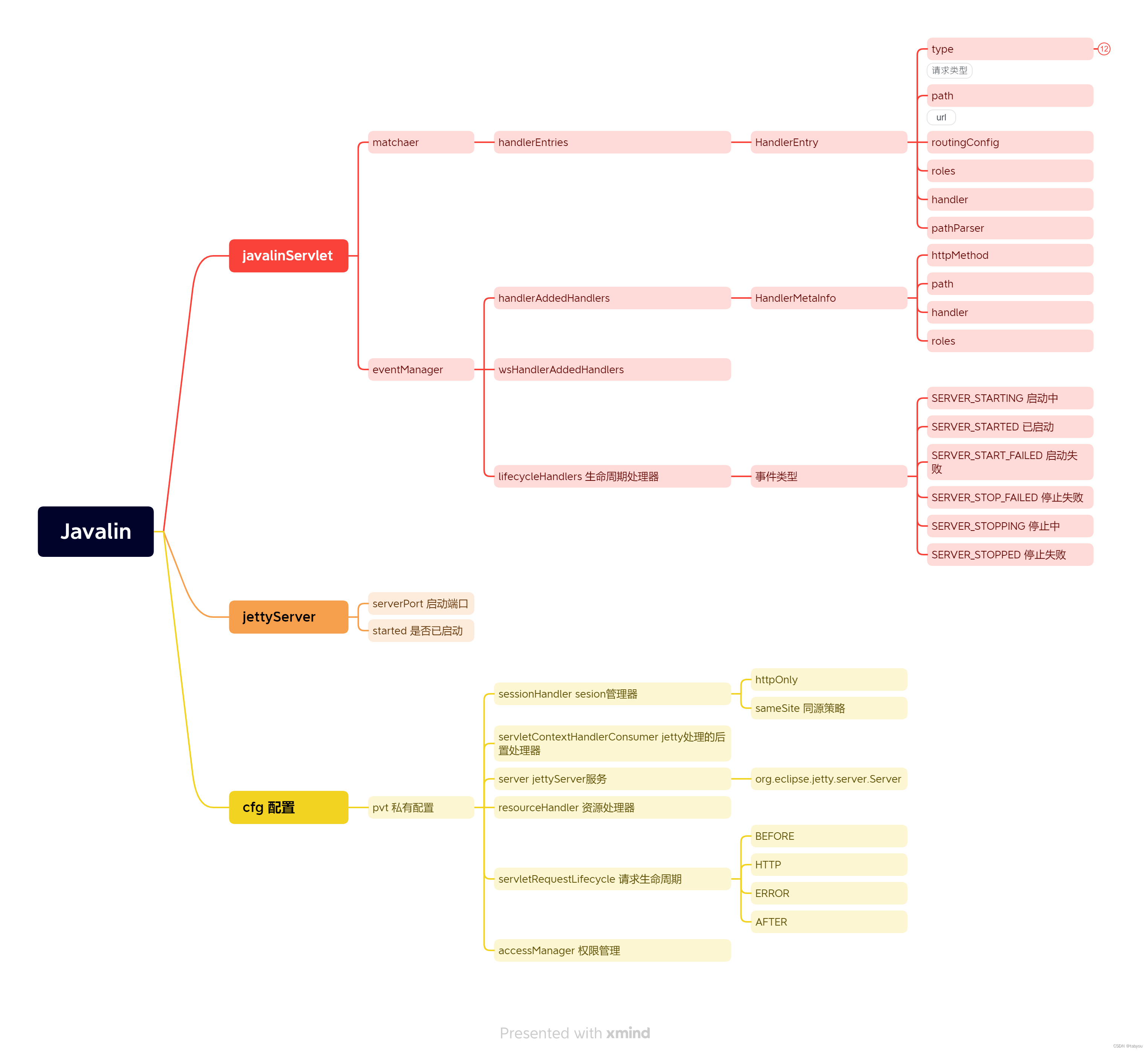
Javalin解构
Javalin Javalin是一个轻量级http框架,我们可以很容易的了解请求的处理过程及其设计,具有较高的学习意义。 从demo说起 public static void main(String[] args) {Javalin app Javalin.create(config -> {System.out.println("用户配置"…...
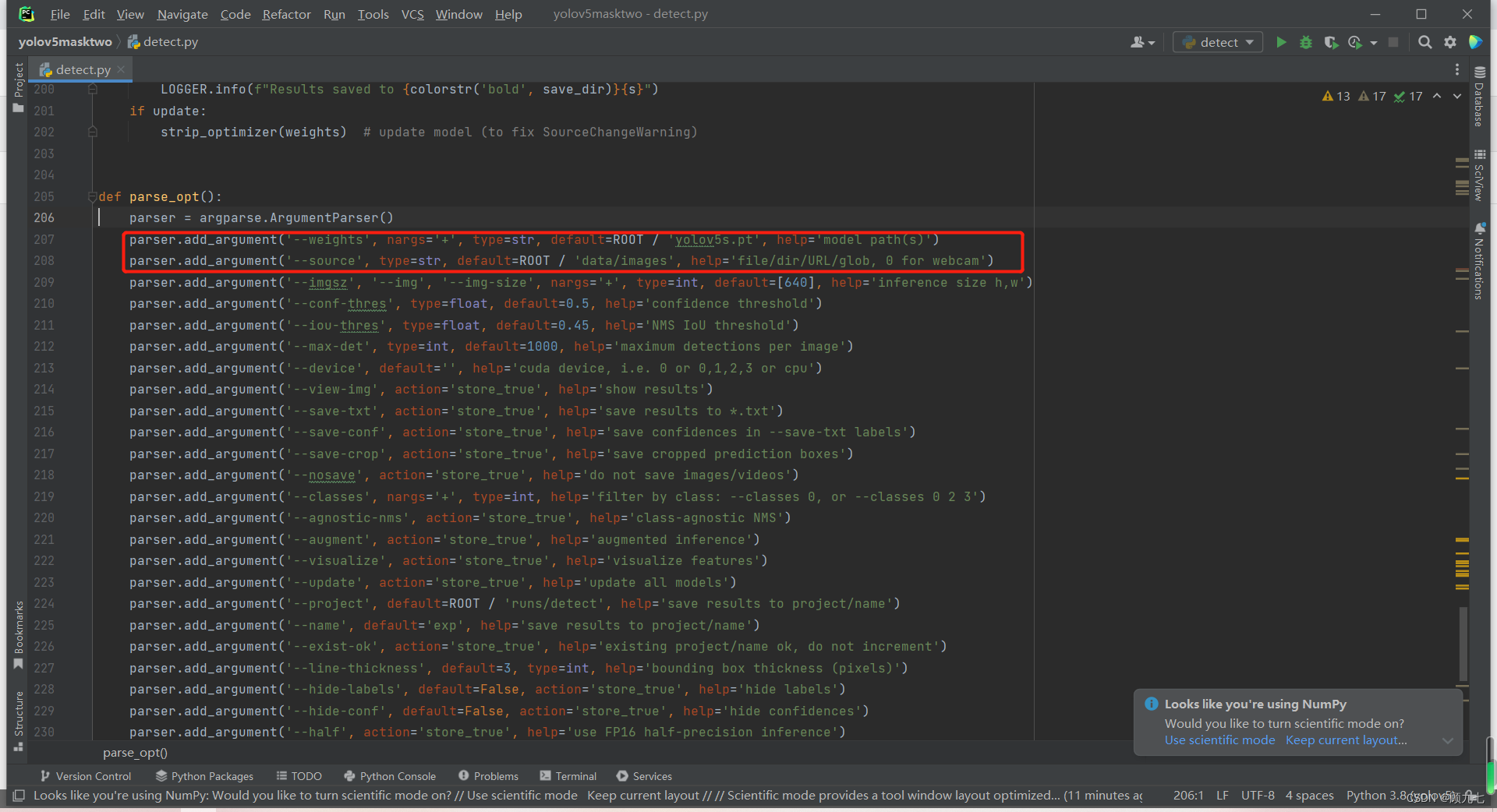
yolov5算法,训练模型,模型检测
嘟嘟嘟嘟!工作需要,所以学习了下yolov5算法。是干什么的呢? 通俗来说,可以将它看做是一个小孩儿,通过成年人(开发人员)提供的大量图片的学习,让自己知道我看到的哪些场景需要提醒给成…...

linux系统防火墙开放端口
linux系统防火墙开放端口 在外部访问CentOS中部署应用时,需要通过防火墙管理软件,开端口,或者直接关闭防火墙进行解决(不建议) 加粗样式 常用命令: systemctl start firewalld #启动 systemctl stop firewalld #停止 systemctl status firewalld #查看…...

CSAPP第九章 虚拟内存
理解虚拟内存的原因 本章前部分描述虚拟内存是如何工作的,后一部分描述应用程序如何使用和管理虚拟内存 物理和虚拟寻址 虚拟内存作为缓存的工具 页表 页命中 缺页 虚拟内存作为内存管理的工具 简化链接,简化加载,简化共享,简化…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
