当前位置： 首页 > news >正文

Android kotlin 系列讲解（进阶篇）高级项目架构模式 - MVVM

news 2026/2/8 19:34:38

<<返回总目录

1、MVVM是什么

MVVM是Model-View-ViewModel的缩写，是一种高级项目架构模式。
 
MVVM架构可以将程序结构主要分成三个部分：

  • Model：数据模型部分，包括从服务端获取的json数据或者从本地获取的数据等等
  • View：界面展示部分(Activity,Fragment,控件View等等)
  • ViewModel：一个连接数据模型和界面展示的桥梁，从而实现让业务逻辑和界面展示分离的程序结构设计

2、MVVM项目架构示意图：

可以看到，平时写的Activity、Fragment、等与界面有关的东西就是在UI控件层中的。ViewModel层用于持有和UI元素相关的数据，以保证这些数据在屏障旋转时不会丢失，并且还要提供接口给UI控件层调用以及和仓库层进行通信。仓库层要做的主要工作是判断调用方请求的数据应该是从本地数据源中获取还是从网络数据源中获取，并将获取到的数据返回给调用方。本地数据源可以使用数据库、SharedPreferences等持久化技术来实现，而网络数据源则通常使用Retrofit访问服务器提供的Webservice接口来实现

相关文章：

Android kotlin 系列讲解（进阶篇）高级项目架构模式 - MVVM

<<返回总目录 1、MVVM是什么 MVVM是Model-View-ViewModel的缩写&#xff0c;是一种高级项目架构模式。 MVVM架构可以将程序结构主要分成三个部分&#xff1a; Model&#xff1a;数据模型部分&#xff0c;包括从服务端获取的json数据或者从本地获取的数据等等View&…...

编程日记 2023/5/13 6:32:03

8. 查找

1 题目描述 查找成绩10开启时间2021年09月24日 星期五 18:00折扣0.8折扣时间2021年11月15日 星期一 00:00允许迟交否关闭时间2021年11月23日 星期二 00:00 输入 n(n ≤ 10^6)个不超过 10^9的单调不减的&#xff08;就是后面的数字不小于前面的数字&#xff09;非负整数 &#…...

编程日记 2023/5/13 6:32:01

二分查找算法

感谢“五点七边”工作室的算法讲解&#xff0c;详细内容可以参考视频讲解 二分查找为什么总是写错&#xff1f;_哔哩哔哩_bilibili 此处仅是个人学习总结 以target等于5为例&#xff0c;输入: 1 2 3 5 5 5 8 9 1. 找到第一个 > target 的元素 判断条件 < target&am…...

编程日记 2023/5/13 6:31:58

Git(3)之远程服务器

Git基础之远程服务器 Author&#xff1a;onceday date&#xff1a;2023年3月5日 满满长路有人对你微笑过嘛… windows安装可参考文章&#xff1a;git简易配置_onceday_CSDN博客 參考文档&#xff1a; 《progit2.pdf》&#xff0c;Progit2 Github。《git-book.pdf》 文章目…...

编程日记 2023/5/13 6:31:56

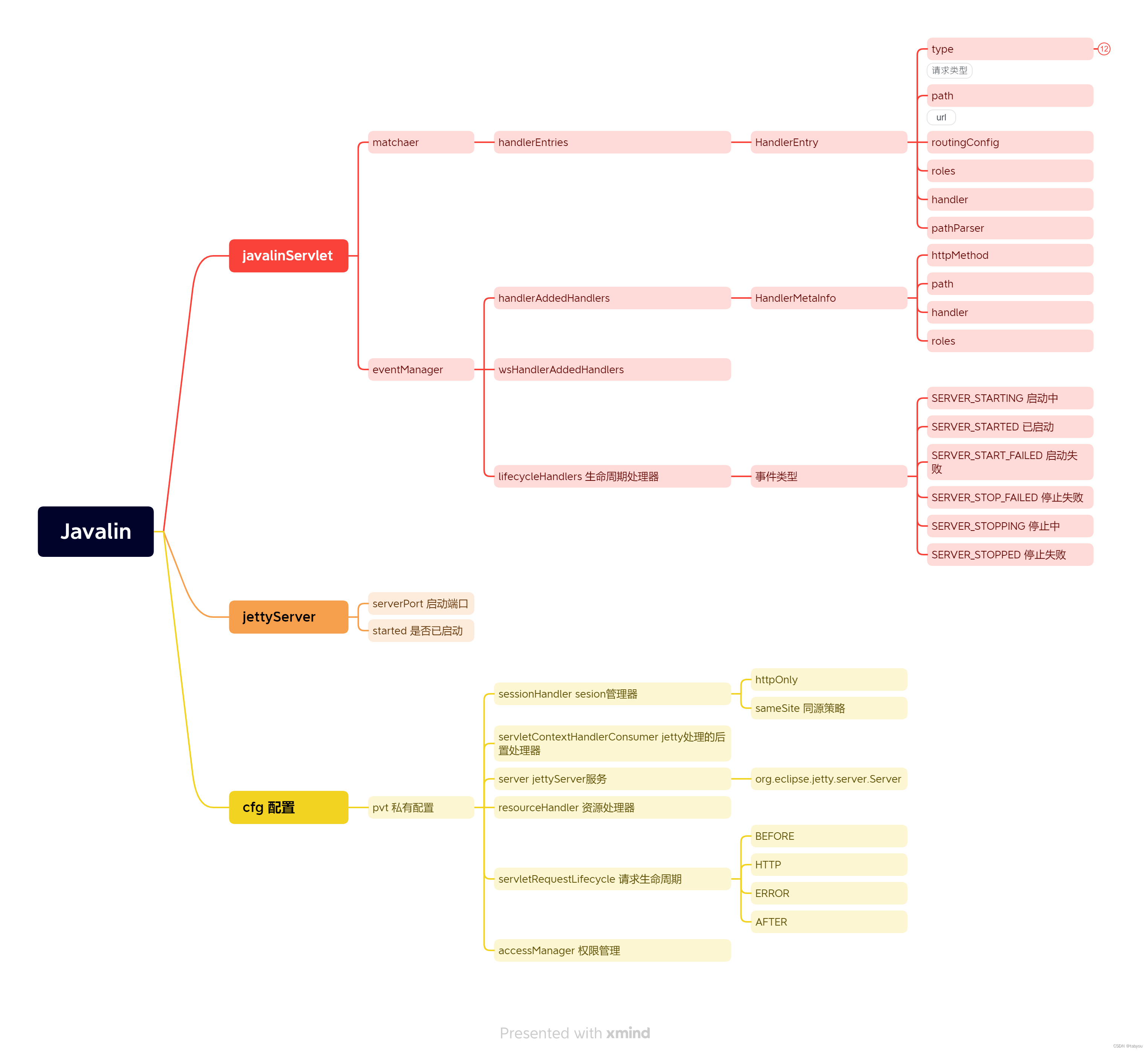
Javalin解构

Javalin Javalin是一个轻量级http框架&#xff0c;我们可以很容易的了解请求的处理过程及其设计&#xff0c;具有较高的学习意义。 从demo说起 public static void main(String[] args) {Javalin app Javalin.create(config -> {System.out.println("用户配置"…...

编程日记 2023/5/13 6:31:54

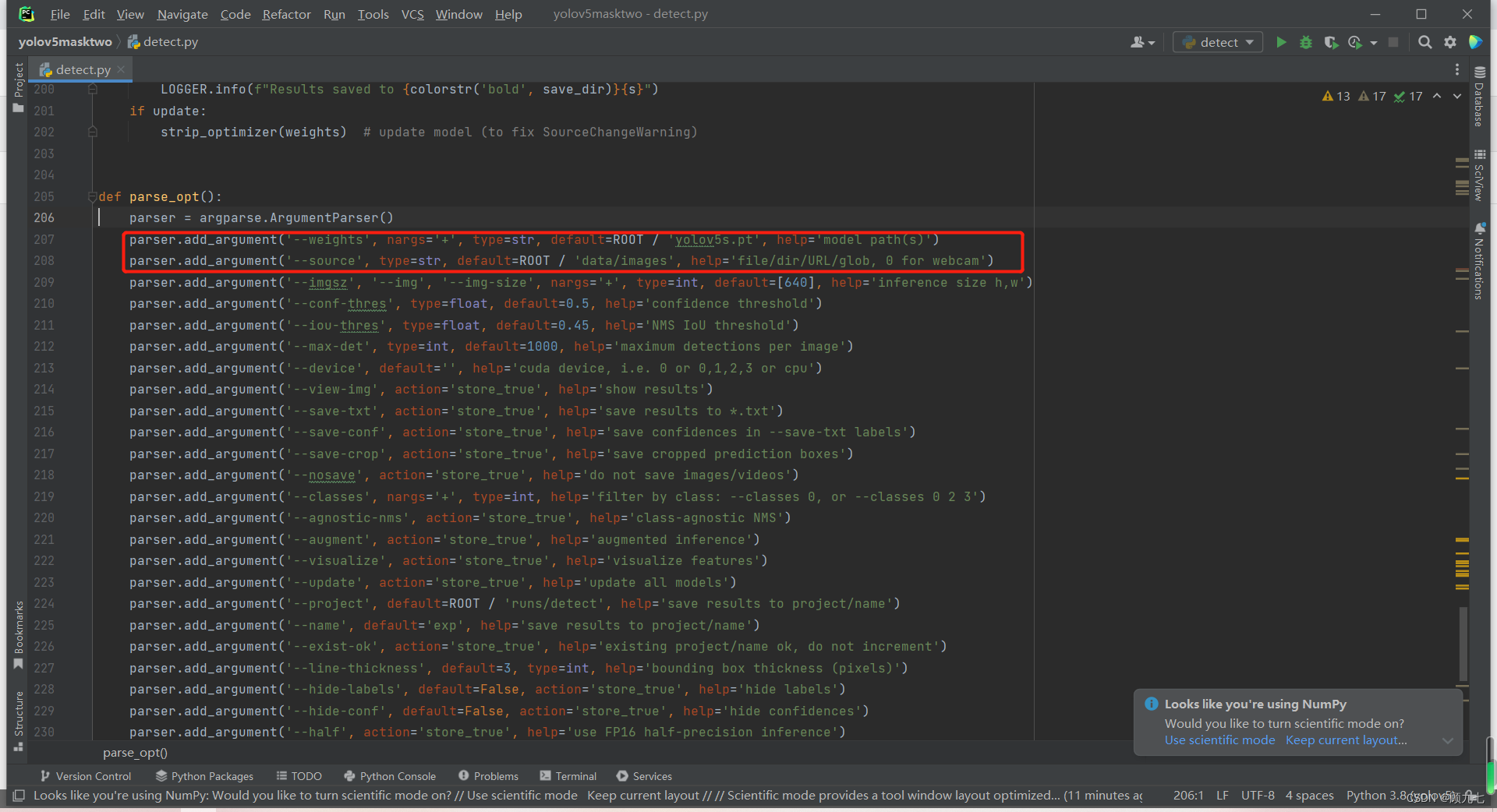
yolov5算法，训练模型，模型检测

嘟嘟嘟嘟&#xff01;工作需要&#xff0c;所以学习了下yolov5算法。是干什么的呢&#xff1f; 通俗来说&#xff0c;可以将它看做是一个小孩儿&#xff0c;通过成年人&#xff08;开发人员&#xff09;提供的大量图片的学习&#xff0c;让自己知道我看到的哪些场景需要提醒给成…...

编程日记 2023/5/13 6:31:51

linux系统防火墙开放端口

linux系统防火墙开放端口 在外部访问CentOS中部署应用时&#xff0c;需要通过防火墙管理软件,开端口,或者直接关闭防火墙进行解决(不建议) 加粗样式 常用命令&#xff1a; systemctl start firewalld #启动 systemctl stop firewalld #停止 systemctl status firewalld #查看…...

编程日记 2023/5/13 6:31:49

CSAPP第九章 虚拟内存

理解虚拟内存的原因 本章前部分描述虚拟内存是如何工作的&#xff0c;后一部分描述应用程序如何使用和管理虚拟内存 物理和虚拟寻址 虚拟内存作为缓存的工具 页表 页命中 缺页 虚拟内存作为内存管理的工具 简化链接&#xff0c;简化加载&#xff0c;简化共享&#xff0c;简化…...

编程日记 2023/5/13 6:31:47

numpy数组与矩阵运算（二）

文章目录矩阵生成与常用操作矩阵生成矩阵转置查看矩阵特性矩阵乘法计算相关系数矩阵计算方差、协方差、标准差计算特征值与特征向量计算逆矩阵求解线性方程组奇异值分解函数向量化矩阵生成与常用操作 矩阵生成 扩展库numpy中提供的matrix()函数可以用来把列表、元组、range对…...

编程日记 2023/5/13 6:31:44

Dubbo 中 Zookeeper 注册中心原理分析

Dubbo 中 Zookeeper 注册中心原理分析 文章目录Dubbo 中 Zookeeper 注册中心原理分析一、ZooKeeper注册中心1.1 ZooKeeper数据结构1.2 ZooKeeper的Watcher机制1.3 ZooKeeper会话机制1.4 使用ZooKeeper作为注册中心二、源码分析2.1 AbstractRegistry2.2 FailbackRegistry2.2.1 核…...

编程日记 2023/5/13 6:31:42

素数产生新的算法（由筛法减法改为增加法）--哥德巴赫猜想的第一次实际应用

素数产生新的算法&#xff08;由筛法减法改为增加法&#xff09;--哥德巴赫猜想的第一次实际应用 摘要&#xff1a;长期以来&#xff0c;人们认为哥德巴赫猜想没有什么实际应用的。 现在&#xff0c;我假设这个不是猜想&#xff0c;而是定理或公理&#xff0c;就产生了新的应用…...

编程日记 2023/5/13 6:31:40

递归-需要满足三个条件

一&#xff0c;概述 递归是一种应用非常广泛的算法&#xff08;或者编程技巧&#xff09;。很多数据结构和算法的编码实现都要用到递归&#xff0c;比如 DFS 深度优先搜索、前中后序二叉树遍历等。 去的过程叫“递”&#xff0c;回来的过程叫“归”。基本上所有的递归问题都可…...

编程日记 2023/5/13 6:31:38

【剑指Offer-Java】两个栈实现队列

题目 用两个栈实现一个队列。队列的声明如下&#xff0c;请实现它的两个函数 appendTail 和 deleteHead &#xff0c;分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素&#xff0c;deleteHead 操作返回 -1 ) 输入&#xff1a; [“CQueue”,“appendT…...

编程日记 2023/5/13 6:31:35

Allegro如何将Waived掉的DRC显示或隐藏操作指导

Allegro如何将Waived掉的DRC显示或隐藏操作指导 在用Allegro做PCB设计的时候，如果遇到正常的DRC，可以用Waive的命令将DRC不显示，如下图 当DRC被Waive掉的时候，如何将DRC再次显示出来。类似下图效果 具体操作如下 点击Display...

编程日记 2023/5/13 6:31:33

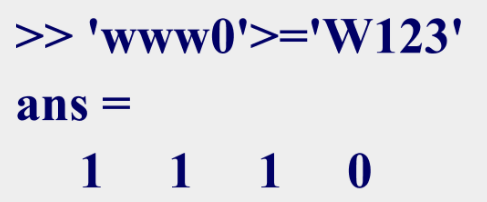
MATLAB——数据及其运算

MATLAB数值数据数值数据类型的分类1&#xff0e;整型整型数据是不带小数的数&#xff0c;有带符号整数和无符号整数之分。表中列出了各种整型数据的取值范围和对应的转换函数。2&#xff0e;浮点型浮点型数据有单精度(single&#xff09;和双精度&#xff08;(double)之分&…...

编程日记 2023/5/13 6:31:31

【微信小程序】-- 页面导航 -- 声明式导航（二十二）

&#x1f48c; 所属专栏&#xff1a;【微信小程序开发教程】 &#x1f600; 作  者&#xff1a;我是夜阑的狗&#x1f436; &#x1f680; 个人简介&#xff1a;一个正在努力学技术的CV工程师&#xff0c;专注基础和实战分享 &#xff0c;欢迎咨询&#xff01; &…...

编程日记 2023/5/13 6:31:28

gdb查看汇编代码的例子

gdb查看汇编代码的例子 操作步骤 用 gdb 启动可执行文件&#xff1a;gdb executable_file在 gdb 中设置断点&#xff1a;break function_name 或者 break *memory_address运行程序&#xff1a;run当程序停止在断点处时&#xff0c;使用 disassemble 命令来查看汇编代码&#…...

编程日记 2023/5/13 6:31:26

第四讲：如何将本地代码与服务器代码保持实时同步

一、前言 在我们进行 Ambari 二次开发时，通常会先在服务器上部署一套可以使用的 Ambari 环境。 二次开发，就肯定是要改动代码的，我们不能老是在服务器上用vim编辑文件，那样效率太低，始终不是长久之计。 所以我们需要在本地打开我们的Ambari源码项目，比如用idea工具，可…...

编程日记 2023/5/13 6:31:24

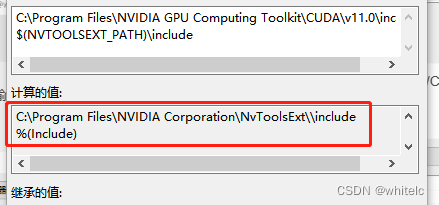
cuda调试（一）vs2019-windows-Nsight system--nvtx使用，添加nvToolsExt.h文件

cuda调试 由于在编程过程中发现不同的网格块的结构&#xff0c;对最后的代码结果有影响&#xff0c;所以想记录一下解决办法。 CUDA的Context、Stream、Warp、SM、SP、Kernel、Block、Grid cuda context (上下文) context类似于CPU进程上下&#xff0c;表示由管理层 Drive …...

编程日记 2023/5/16 18:39:54

向Spring容器中注入bean有哪几种方式？

文章前言&#xff1a; 写这篇文章的时候&#xff0c;我正在手机上看腾讯课堂的公开课&#xff0c;有讲到 Spring IOC 创建bean有哪几种方式&#xff0c;视频中有提到过 set注入、构造器注入、注解方式注入等等&#xff1b;于是&#xff0c;就想到了写一篇《Spring注入bean有几种…...

编程日记 2023/5/13 6:31:21

【大模型RAG】拍照搜题技术架构速览：三层管道、两级检索、兜底大模型

摘要 拍照搜题系统采用“三层管道&#xff08;多模态 OCR → 语义检索 → 答案渲染&#xff09;、两级检索&#xff08;倒排 BM25 向量 HNSW&#xff09;并以大语言模型兜底”的整体框架&#xff1a; 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后&#xff0c;分别用…...

编程新知 2026/2/8 4:32:38

ubuntu搭建nfs服务centos挂载访问

在Ubuntu上设置NFS服务器 在Ubuntu上&#xff0c;你可以使用apt包管理器来安装NFS服务器。打开终端并运行&#xff1a; sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享&#xff0c;例如/shared&#xff1a; sudo mkdir /shared sud…...

编程新知 2026/2/6 23:18:59

基于Flask实现的医疗保险欺诈识别监测模型

基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施&#xff0c;由雇主和个人按一定比例缴纳保险费&#xff0c;建立社会医疗保险基金&#xff0c;支付雇员医疗费用的一种医疗保险制度&#xff0c; 它是促进社会文明和进步的…...

编程新知 2026/1/24 14:59:08

sqlserver 根据指定字符 解析拼接字符串

DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

编程新知 2025/10/29 4:33:03

数据库分批入库

今天在工作中&#xff0c;遇到一个问题&#xff0c;就是分批查询的时候&#xff0c;由于批次过大导致出现了一些问题&#xff0c;一下是问题描述和解决方案&#xff1a; 示例&#xff1a; // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

编程新知 2026/1/8 11:38:36

OpenLayers 分屏对比(地图联动)

注&#xff1a;当前使用的是 ol 5.3.0 版本&#xff0c;天地图使用的key请到天地图官网申请&#xff0c;并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能&#xff0c;和卷帘图层不一样的是&#xff0c;分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

编程新知 2025/12/25 18:22:43

JAVA后端开发——多租户

数据隔离是多租户系统中的核心概念&#xff0c;确保一个租户&#xff08;在这个系统中可能是一个公司或一个独立的客户&#xff09;的数据对其他租户是不可见的。在 RuoYi 框架&#xff08;您当前项目所使用的基础框架&#xff09;中&#xff0c;这通常是通过在数据表中增加一个…...

编程新知 2025/12/18 8:35:12

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制

使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下&#xff0c;限制某个 IP 的访问频率是非常重要的&#xff0c;可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案&#xff0c;使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

编程新知 2025/10/22 6:06:44

GO协程(Goroutine)问题总结

在使用Go语言来编写代码时&#xff0c;遇到的一些问题总结一下 [参考文档]&#xff1a;https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现&#xff1a; 今天在看到这个教程的时候&#xff0c;在自己的电…...

编程新知 2026/1/31 6:53:53

从 GreenPlum 到镜舟数据库：杭银消费金融湖仓一体转型实践

作者&#xff1a;吴岐诗&#xff0c;杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言&#xff1a;融合数据湖与数仓的创新之路 在数字金融时代&#xff0c;数据已成为金融机构的核心竞争力。杭银消费金…...

编程新知 2026/1/31 12:30:32