numpy数组与矩阵运算(二)
文章目录
- 矩阵生成与常用操作
- 矩阵生成
- 矩阵转置
- 查看矩阵特性
- 矩阵乘法
- 计算相关系数矩阵
- 计算方差、协方差、标准差
- 计算特征值与特征向量
- 计算逆矩阵
- 求解线性方程组
- 奇异值分解
- 函数向量化
矩阵生成与常用操作
矩阵生成
扩展库numpy中提供的matrix()函数可以用来把列表、元组、range对象等Python可迭代对象转换为矩阵。
>>> import numpy as np
>>> x=np.matrix([[1,2,3],[4,5,6]])
>>> y=np.matrix([1,2,3,4,5,6])
>>> # 对矩阵x来说,x[1,1]和x[1][1]的含义不一样
>>> x
matrix([[1, 2, 3],[4, 5, 6]])
>>> y
matrix([[1, 2, 3, 4, 5, 6]])
>>> x[1,1]
5
矩阵转置
>>> x.T
matrix([[1, 4],[2, 5],[3, 6]])
>>> y.T
matrix([[1],[2],[3],[4],[5],[6]])
查看矩阵特性
>>> x=np.matrix([[1,2,3],[4,5,6]])
>>> x.mean() # 所有元素平均值
3.5
>>> x.mean(axis=0) # 纵向平均值
matrix([[2.5, 3.5, 4.5]])
>>> x.mean(axis=1) # 横向平均值
matrix([[2.],[5.]])
>>> x.sum() # 所有元素之和
21
>>> x.max(axis=1) # 横向最大值
matrix([[3],[6]])
>>> x.argmax(axis=1) # 横向最大值下标
matrix([[2],[2]], dtype=int64)
>>> x.diagonal() # 对角线元素
matrix([[1, 5]])
>>> x.nonzero() # 非0元素下标
(array([0, 0, 0, 1, 1, 1], dtype=int64), array([0, 1, 2, 0, 1, 2], dtype=int64))
>>> # 行下标列表和列下标列表
矩阵乘法
一个mxp的矩阵和一个pxn的矩阵,它们的乘积为一个mxn的矩阵
>>> x=np.matrix([[1,2,3],[4,5,6]])
>>> y=np.matrix([[1,2],[3,4],[5,6]])
>>> x*y
matrix([[22, 28],[49, 64]])
计算相关系数矩阵
>>> np.corrcoef([1,2,3,4],[4,3,2,1]) # 负相关,变化反向相反
array([[ 1., -1.],[-1., 1.]])
>>> np.corrcoef([1,2,3,4],[8,3,2,1]) # 负相关,变化反向相反
array([[ 1. , -0.91350028],[-0.91350028, 1. ]])
>>> np.corrcoef([1,2,3,4],[1,2,3,4]) # 正相关,变化反向一致
array([[1., 1.],[1., 1.]])
>>> np.corrcoef([1,2,3,4],[1,2,3,40]) # 正相关,变化趋势接近
array([[1. , 0.8010362],[0.8010362, 1. ]])
计算方差、协方差、标准差
>>> np.cov([1,1,1,1,1]) # 方差
array(0.)
>>> np.std([1,1,1,1,1]) # 标准差
0.0
>>> x=[-2.1,-1,4.3]
>>> y=[3,1.1,0.12]
>>> X=np.vstack((x,y))
>>> X
array([[-2.1 , -1. , 4.3 ],[ 3. , 1.1 , 0.12]])
>>> np.cov(X) # 协方差
array([[11.71 , -4.286 ],[-4.286 , 2.14413333]])
>>> np.cov(x,y)
array([[11.71 , -4.286 ],[-4.286 , 2.14413333]])
>>> np.std(X) # 标准差
2.2071223094538484
>>> np.std(X,axis=1)
array([2.79404128, 1.19558447])
>>> np.cov(x) # 方差
array(11.71)
计算特征值与特征向量
>>> A=np.array([[1,-3,3],[3,-5,3],[6,-6,4]])
>>> e,v=np.linalg.eig(A) # 特征值与特征向量
>>> e
array([ 4.+0.00000000e+00j, -2.+1.10465796e-15j, -2.-1.10465796e-15j])
>>> v
array([[-0.40824829+0.j , 0.24400118-0.40702229j,0.24400118+0.40702229j],[-0.40824829+0.j , -0.41621909-0.40702229j,-0.41621909+0.40702229j],[-0.81649658+0.j , -0.66022027+0.j ,-0.66022027-0.j ]])
>>> np.dot(A,v) # 矩阵与特征向量的乘积
array([[-1.63299316+0.00000000e+00j, -0.48800237+8.14044580e-01j,-0.48800237-8.14044580e-01j],[-1.63299316+0.00000000e+00j, 0.83243817+8.14044580e-01j,0.83243817-8.14044580e-01j],[-3.26598632+0.00000000e+00j, 1.32044054-5.55111512e-16j,1.32044054+5.55111512e-16j]])
>>> e*v # 特征值与特征向量的乘积
array([[-1.63299316+0.00000000e+00j, -0.48800237+8.14044580e-01j,-0.48800237-8.14044580e-01j],[-1.63299316+0.00000000e+00j, 0.83243817+8.14044580e-01j,0.83243817-8.14044580e-01j],[-3.26598632+0.00000000e+00j, 1.32044054-7.29317578e-16j,1.32044054+7.29317578e-16j]])
>>> np.isclose(np.dot(A,v),e*v) # 验证两者是否相等
array([[ True, True, True],[ True, True, True],[ True, True, True]])
计算逆矩阵
>>> x=np.matrix([[1,2,3],[4,5,6],[7,8,0]])
>>> y=np.linalg.inv(x) # 计算逆矩阵
>>> y
matrix([[-1.77777778, 0.88888889, -0.11111111],[ 1.55555556, -0.77777778, 0.22222222],[-0.11111111, 0.22222222, -0.11111111]])
>>> x*y # 对角线元素为1,其他元素为0或近似为0
matrix([[ 1.00000000e+00, 5.55111512e-17, 1.38777878e-17],[ 5.55111512e-17, 1.00000000e+00, 2.77555756e-17],[ 1.77635684e-15, -8.88178420e-16, 1.00000000e+00]])
>>> y*x
matrix([[ 1.00000000e+00, -1.11022302e-16, 0.00000000e+00],[ 8.32667268e-17, 1.00000000e+00, 2.22044605e-16],[ 6.93889390e-17, 0.00000000e+00, 1.00000000e+00]])
求解线性方程组
{a11x1+a12x2+...+a1nxn=b1a21x1+a22x2+...+a2nxn=b2...an1x1+an2x2+...+annxn=bn\begin{cases} a11x1+a12x2+...+a1nxn=b1\\ a21x1+a22x2+...+a2nxn=b2\\ ...\\ an1x1+an2x2+...+annxn=bn\\ \end{cases}⎩⎨⎧a11x1+a12x2+...+a1nxn=b1a21x1+a22x2+...+a2nxn=b2...an1x1+an2x2+...+annxn=bn
可以写作矩阵相乘的形式 ax=b
其中,a为nxn的矩阵,x和b为nx1的矩阵
>>> a=np.array([[3,1],[1,2]]) # 系数矩阵
>>> b=np.array([9,8]) # 系数矩阵
>>> x=np.linalg.solve(a,b) # 求解
>>> x
array([2., 3.])
>>> np.dot(a,x) # 验证
array([9., 8.])
>>> np.linalg.lstsq(a,b) # 最小二乘解,返回解、余项、a的秩、a的奇异值Warning (from warnings module):File "<pyshell#77>", line 1
FutureWarning: `rcond` parameter will change to the default of machine precision times ``max(M, N)`` where M and N are the input matrix dimensions.
To use the future default and silence this warning we advise to pass `rcond=None`, to keep using the old, explicitly pass `rcond=-1`.
(array([2., 3.]), array([], dtype=float64), 2, array([3.61803399, 1.38196601]))
>>>
有报错不要慌
>>> np.linalg.lstsq(a,b,rcond=None) # 最小二乘解,返回解、余项、a的秩、a的奇异值
(array([2., 3.]), array([], dtype=float64), 2, array([3.61803399, 1.38196601]))
可以写个方程去尝试一下,我试了一下,应该是没有问题的。
奇异值分解
把矩阵a分解为u*np.diag(s)*v的形式并返回u、s和v。其中数组s中的元素是矩阵a的元素值
>>> import numpy as np
>>> a=np.matrix([[1,2,3],[4,5,6],[7,8,9]])
>>> u,s,v=np.linalg.svd(a) # 奇异值分解
>>> u
matrix([[-0.21483724, 0.88723069, 0.40824829],[-0.52058739, 0.24964395, -0.81649658],[-0.82633754, -0.38794278, 0.40824829]])
>>> s
array([1.68481034e+01, 1.06836951e+00, 4.41842475e-16])
>>> v
matrix([[-0.47967118, -0.57236779, -0.66506441],[-0.77669099, -0.07568647, 0.62531805],[-0.40824829, 0.81649658, -0.40824829]])
>>> u*np.diag(s)*v # 验证
matrix([[1., 2., 3.],[4., 5., 6.],[7., 8., 9.]])
函数向量化
>>> mat=np.matrix([[1,2,3],[4,5,6]])
>>> mat
matrix([[1, 2, 3],[4, 5, 6]])
>>> import math
>>> vecFactorial=np.vectorize(math.factorial) # 函数向量化
>>> vecFactorial(mat)
matrix([[ 1, 2, 6],[ 24, 120, 720]])
相关文章:
)
numpy数组与矩阵运算(二)
文章目录矩阵生成与常用操作矩阵生成矩阵转置查看矩阵特性矩阵乘法计算相关系数矩阵计算方差、协方差、标准差计算特征值与特征向量计算逆矩阵求解线性方程组奇异值分解函数向量化矩阵生成与常用操作 矩阵生成 扩展库numpy中提供的matrix()函数可以用来把列表、元组、range对…...

Dubbo 中 Zookeeper 注册中心原理分析
Dubbo 中 Zookeeper 注册中心原理分析 文章目录Dubbo 中 Zookeeper 注册中心原理分析一、ZooKeeper注册中心1.1 ZooKeeper数据结构1.2 ZooKeeper的Watcher机制1.3 ZooKeeper会话机制1.4 使用ZooKeeper作为注册中心二、源码分析2.1 AbstractRegistry2.2 FailbackRegistry2.2.1 核…...
--哥德巴赫猜想的第一次实际应用)
素数产生新的算法(由筛法减法改为增加法)--哥德巴赫猜想的第一次实际应用
素数产生新的算法(由筛法减法改为增加法)--哥德巴赫猜想的第一次实际应用 摘要:长期以来,人们认为哥德巴赫猜想没有什么实际应用的。 现在,我假设这个不是猜想,而是定理或公理,就产生了新的应用…...

递归-需要满足三个条件
一,概述 递归是一种应用非常广泛的算法(或者编程技巧)。很多数据结构和算法的编码实现都要用到递归,比如 DFS 深度优先搜索、前中后序二叉树遍历等。 去的过程叫“递”,回来的过程叫“归”。基本上所有的递归问题都可…...

【剑指Offer-Java】两个栈实现队列
题目 用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 ) 输入: [“CQueue”,“appendT…...

Allegro如何将Waived掉的DRC显示或隐藏操作指导
Allegro如何将Waived掉的DRC显示或隐藏操作指导 在用Allegro做PCB设计的时候,如果遇到正常的DRC,可以用Waive的命令将DRC不显示,如下图 当DRC被Waive掉的时候,如何将DRC再次显示出来。类似下图效果 具体操作如下 点击Display...
MATLAB——数据及其运算
MATLAB数值数据数值数据类型的分类1.整型整型数据是不带小数的数,有带符号整数和无符号整数之分。表中列出了各种整型数据的取值范围和对应的转换函数。2.浮点型浮点型数据有单精度(single)和双精度((double)之分&…...

【微信小程序】-- 页面导航 -- 声明式导航(二十二)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

gdb查看汇编代码的例子
gdb查看汇编代码的例子 操作步骤 用 gdb 启动可执行文件:gdb executable_file在 gdb 中设置断点:break function_name 或者 break *memory_address运行程序:run当程序停止在断点处时,使用 disassemble 命令来查看汇编代码&#…...

第四讲:如何将本地代码与服务器代码保持实时同步
一、前言 在我们进行 Ambari 二次开发时,通常会先在服务器上部署一套可以使用的 Ambari 环境。 二次开发,就肯定是要改动代码的,我们不能老是在服务器上用vim编辑文件,那样效率太低,始终不是长久之计。 所以我们需要在本地打开我们的Ambari源码项目,比如用idea工具,可…...
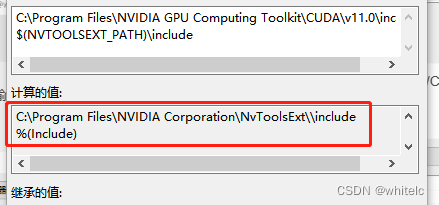
cuda调试(一)vs2019-windows-Nsight system--nvtx使用,添加nvToolsExt.h文件
cuda调试 由于在编程过程中发现不同的网格块的结构,对最后的代码结果有影响,所以想记录一下解决办法。 CUDA的Context、Stream、Warp、SM、SP、Kernel、Block、Grid cuda context (上下文) context类似于CPU进程上下,表示由管理层 Drive …...

向Spring容器中注入bean有哪几种方式?
文章前言: 写这篇文章的时候,我正在手机上看腾讯课堂的公开课,有讲到 Spring IOC 创建bean有哪几种方式,视频中有提到过 set注入、构造器注入、注解方式注入等等;于是,就想到了写一篇《Spring注入bean有几种…...

如何用 Python采集 <豆某yin片>并作词云图分析 ?
嗨害大家好鸭!我是小熊猫~ 总有那么一句银幕台词能打动人心 总有那么一幕名导名作念念不忘 不知道大家有多久没有放松一下了呢? 本次就来给大家采集一下某瓣电影并做词云分析 康康哪一部才是大家心中的经典呢? 最近又有哪一部可能会成为…...

Python装饰器的具体实用示例
示例1:普通装饰器 def name(n):def func(x):res n(xx)return resreturn funcname def run(x): # run name(run)print(x)if __name__ __main__:run(1) # 2def name(n):def func(*x):res n(xx)return resreturn funcname def run(x): # run name(run)pr…...

谈谈我对Retrofit源码的理解
文章目录一、Retrofit简介二、使用介绍2.1 app / build.gradle添加依赖2.2 创建 Retrofit 实例2.3 创建 API 接口定义文件2.4 使用 Retrofit 进行网络请求三、源码分析3.1 创建 Retrofit 实例: 建造者模式创建Retrofit3.2 实例化API接口: 动态代理模式3.3 获取Observable返回值…...
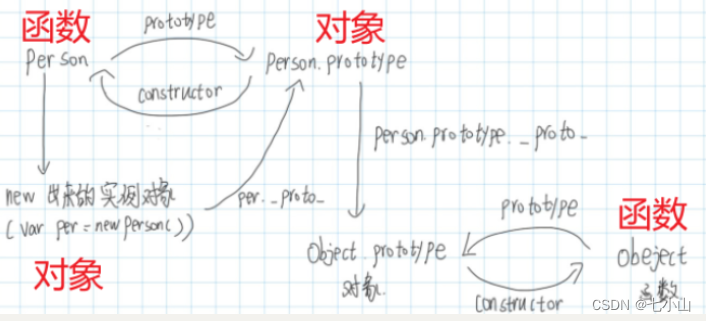
八股文(三)
目录 一、 如何理解原型与原型链 二、 js继承 三、 vuex的使用 1.mutation和action的区别 mutation action 2.Vuex都有哪些API 四、 前端性能优化方法 五、 类型判断 题目 (1)typeof判断哪个类型会出错(即结果不准确)&…...

2023最新实施工程师面试题
1、两电脑都在同一个网络环境中,A 电脑访问不到 B 电脑的共享文件。此现象可能是哪些 方面所导致?怎样处理? 答:首先你要确定是不是在一个工作组内,只有在一个工作组内才可以共享文件,然后看一个看一看有没有防火墙之类的,然后确定文件是不是已经共享 2、 电脑开机时风扇…...
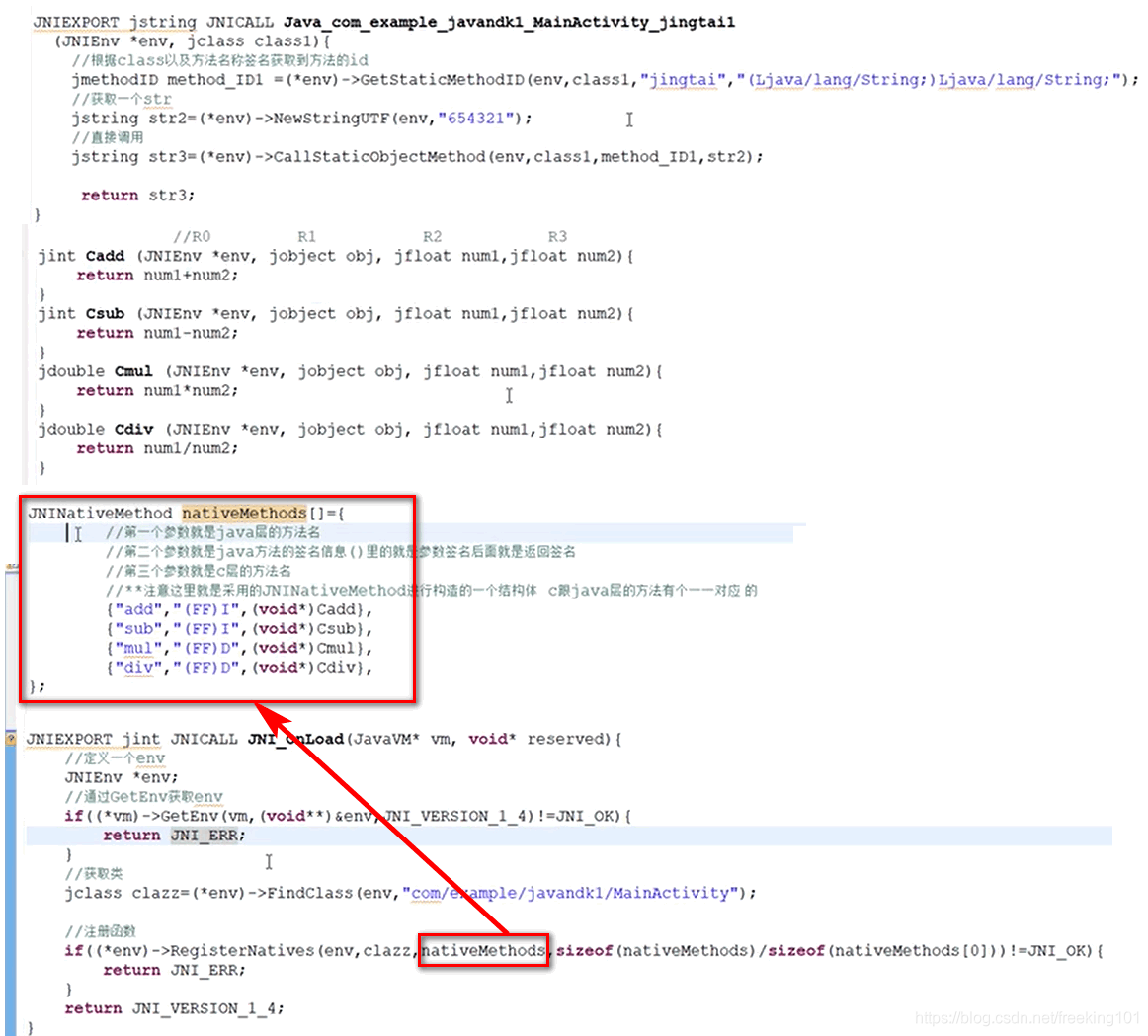
安卓逆向_6 --- JNI 和 NDK
Java 本机接口规范内容:https://docs.oracle.com/en/java/javase/19/docs/specs/jni/index.html JNI官方中文资料:https://blog.csdn.net/yishifu/article/details/52180448 NDK 官方文档:https://developer.android.google.cn/training/ar…...
Pod控制器
K8S之控制器详解#简介#在kubernetes中,按照Pod的创建方式可以将其分为两类:自主式:kubernetes直接创建出来的Pod,这种Pod删除后就没有了,也不会重建。控制器创建pod:通过Pod控制器创建的Pod,这种Pod删除之后还会自动重…...
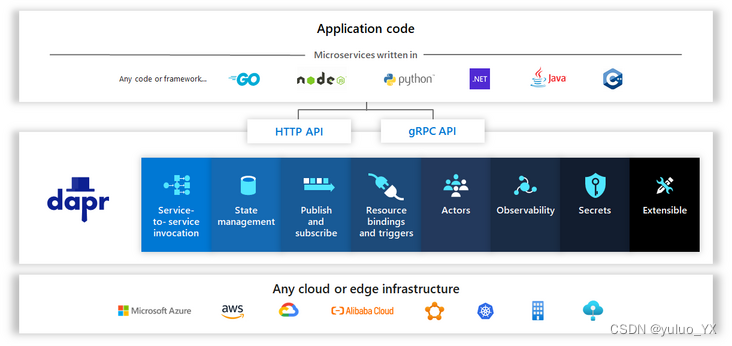
微服务到云原生
微服务到云原生 微服务 微服务架构(Microservice Architecture)是一种架构概念,旨在通过将功能分解到各个离散的服务中以实现对解决方案的解耦。 微服务是一种架构风格,一个大型复杂软件应用由一个或多个微服务组成。系统中的各…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...
