深入理解快速排序算法:从原理到实现
目录
1. 引言
2. 快速排序算法原理
3. 快速排序的时间复杂度分析
4. 快速排序的应用场景
5. 快速排序的优缺点分析
5.1 优点:
5.2 缺点:
6. Java、JavaScript 和 Python 实现快速排序算法
6.1 Java 实现:
6.2 JavaScript 实现:
6.3 Python
7. 总结
1. 引言
快速排序是一种经典的排序算法,它的核心思想是分治和递归。通过将待排序序列分割成较小的子序列,分别对子序列进行排序,最终将子序列合并成有序序列。本文将从原理、时间复杂度、应用场景、优缺点等方面深入探讨快速排序算法,并通过 Java、JavaScript 和 Python 三种编程语言的示例进行说明。

2. 快速排序算法原理
快速排序算法的核心思想是选取一个基准元素,将序列分割成两个子序列,一个子序列中的元素都小于基准元素,另一个子序列中的元素都大于基准元素,然后对这两个子序列分别进行递归排序,最终得到完全有序的序列。
快速排序的步骤如下:
- 从序列中选择一个基准元素(通常选择第一个元素)。
- 将序列中小于基准元素的元素放在基准元素的左边,大于基准元素的元素放在右边,基准元素放在两个子序列的中间位置。
- 对左右两个子序列分别进行递归排序,直到子序列长度为1或0。

3. 快速排序的时间复杂度分析
快速排序算法的时间复杂度取决于基准元素的选择和序列的划分。在最坏情况下,即每次划分都只能将序列分割成一个较小的子序列和一个较大的子序列,时间复杂度为O(n^2)。在平均情况下,快速排序的时间复杂度为O(n log n)。

4. 快速排序的应用场景
快速排序算法适用于处理大规模数据的排序问题,特别是在处理大规模随机数据时表现良好。由于快速排序的时间复杂度较低,因此在需要高效率排序的场景下广泛应用。

5. 快速排序的优缺点分析
5.1 优点:
- 时间复杂度低:在平均情况下,快速排序的时间复杂度为O(n log n),效率较高。
- 原地排序:快速排序是一种原地排序算法,不需要额外的辅助空间。
- 分治思想:快速排序采用分治策略,可以充分利用多核CPU的并行性。
5.2 缺点:
- 不稳定性:由于快速排序是一种交换排序算法,交换过程可能导致相同元素的相对位置发生改变,因此快速排序是一种不稳定的排序算法。
- 对于小规模数据和部分有序数据的处理效率不高:在处理小规模数据或者部分有序数据时,快速排序的效率不如插入排序等算法。

6. Java、JavaScript 和 Python 实现快速排序算法
6.1 Java 实现:
public class QuickSort {public static void quickSort(int[] arr, int low, int high) {if (low < high) {int pivotIndex = partition(arr, low, high);quickSort(arr, low, pivotIndex - 1);quickSort(arr, pivotIndex + 1, high);}}public static int partition(int[] arr, int low, int high) {int pivot = arr[low];int i = low;int j = high;while (i < j) {while (i < j && arr[j] >= pivot) {j--;}arr[i] = arr[j];while (i < j && arr[i] <= pivot) {i++;}arr[j] = arr[i];}arr[i] = pivot;return i;}public static void main(String[] args) {int[] arr = {12, 11, 13, 5, 6};quickSort(arr, 0, arr.length - 1);System.out.println("Sorted array: " + Arrays.toString(arr));}
}
6.2 JavaScript 实现:
function quickSort(arr, low, high) {if (low < high) {let pivotIndex = partition(arr, low, high);quickSort(arr, low, pivotIndex - 1);quickSort(arr, pivotIndex + 1, high);}
}function partition(arr, low, high) {let pivot = arr[low];let i = low;let j = high;while (i < j) {while (i < j && arr[j] >= pivot) {j--;}arr[i] = arr[j];while (i < j && arr[i] <= pivot) {i++;}arr[j] = arr[i];}arr[i] = pivot;return i;
}let arr = [12, 11, 13, 5, 6];
quickSort(arr, 0, arr.length - 1);
console.log("Sorted array: " + arr);
6.3 Python
def quickSort(arr, low, high):if low < high:pivotIndex = partition(arr, low, high)quickSort(arr, low, pivotIndex - 1)quickSort(arr, pivotIndex + 1, high)def partition(arr, low, high):pivot = arr[low]i = lowj = highwhile i < j:while i < j and arr[j] >= pivot:j -= 1arr[i] = arr[j]while i < j and arr[i] <= pivot:i += 1arr[j] = arr[i]arr[i] = pivotreturn iarr = [12, 11, 13, 5, 6]
quickSort(arr, 0, len(arr) - 1)
print("Sorted array:", arr)
7. 总结
通过本文的介绍,我们对快速排序算法有了更深入的理解。从原理到实现,再到时间复杂度分析、应用场景、优缺点等方面,我们对快速排序算法有了全面的认识。同时,通过用 Java、JavaScript 和 Python 三种编程语言实现快速排序算法,我们加深了对这些语言特性和语法的理解,提高了编程能力。
快速排序算法是一种高效的排序算法,在处理大规模数据时表现良好。但也需要注意,在处理小规模数据或者部分有序数据时,快速排序的效率可能不如其他算法。因此,在选择排序算法时,需要根据具体情况综合考虑。
希望本文能够帮助读者更好地理解快速排序算法,并在实践中灵活运用,解决实际问题。同时也希望读者能够继续深入学习和探索,不断提升自己的算法能力和编程技术。

相关文章:

深入理解快速排序算法:从原理到实现
目录 1. 引言 2. 快速排序算法原理 3. 快速排序的时间复杂度分析 4. 快速排序的应用场景 5. 快速排序的优缺点分析 5.1 优点: 5.2 缺点: 6. Java、JavaScript 和 Python 实现快速排序算法 6.1 Java 实现: 6.2 JavaScript 实现&#…...
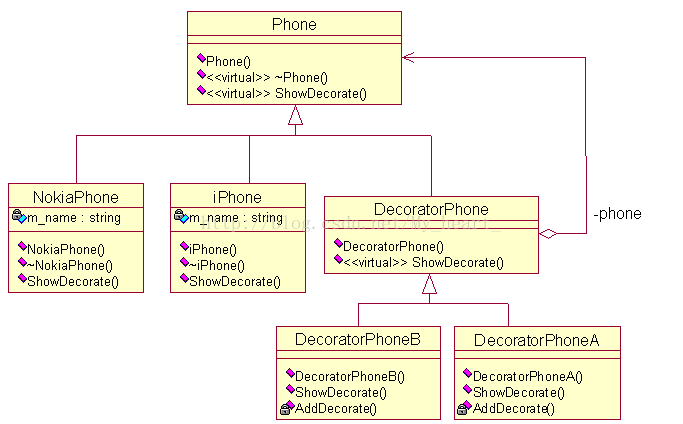
设计模式----装饰器模式
在软件开发过程中,有时想用一些现存的组件。这些组件可能只是完成了一些核心功能。但在不改变其结构的情况下,可以动态地扩展其功能。所有这些都可以釆用装饰器模式来实现。 装饰器模式 允许向一个现有的对象添加新的功能,同时又不改变他的…...
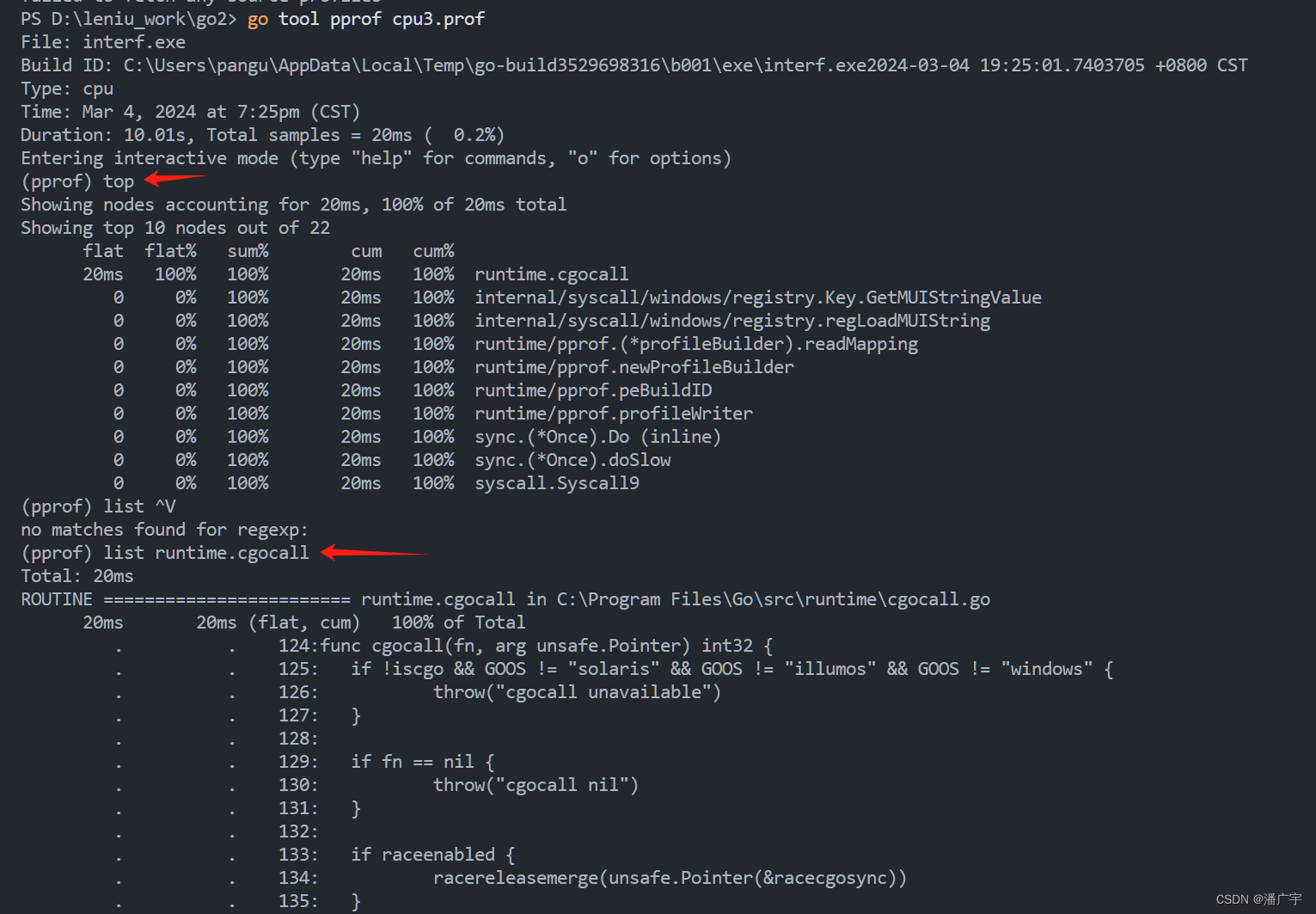
Golang pprof 分析程序的使用内存和执行时间
一、分析程序执行的内存情况 package mainimport ("os""runtime/pprof" )func main() {// ... 你的程序逻辑 ...// 将 HeapProfile 写入文件f, err : os.Create("heap.prof")if err ! nil {panic(err)}defer f.Close()pprof.WriteHeapProfile(f…...
C/C++平方和问题(蓝桥杯)
题目描述: 小明对数位中含有2、0、1、9 的数字很感兴趣,在1 到40 中这样的数包 括1、2、9、10 至32、39 和40,共28 个,他们的和是574,平方和是14362。 注意,平方和是指将每个数分别平方后求和。 请问&#…...

(libusb) usb口自动刷新
文章目录 libusb自动刷新程序Code目录结构Code项目文件usb包code包 效果描述重置reset热拔插使用 END libusb 在操作USB相关内容时,有一个比较著名的库就是libusb。 官方网址:libusb 下载: 下载源码官方编好的库github:Release…...
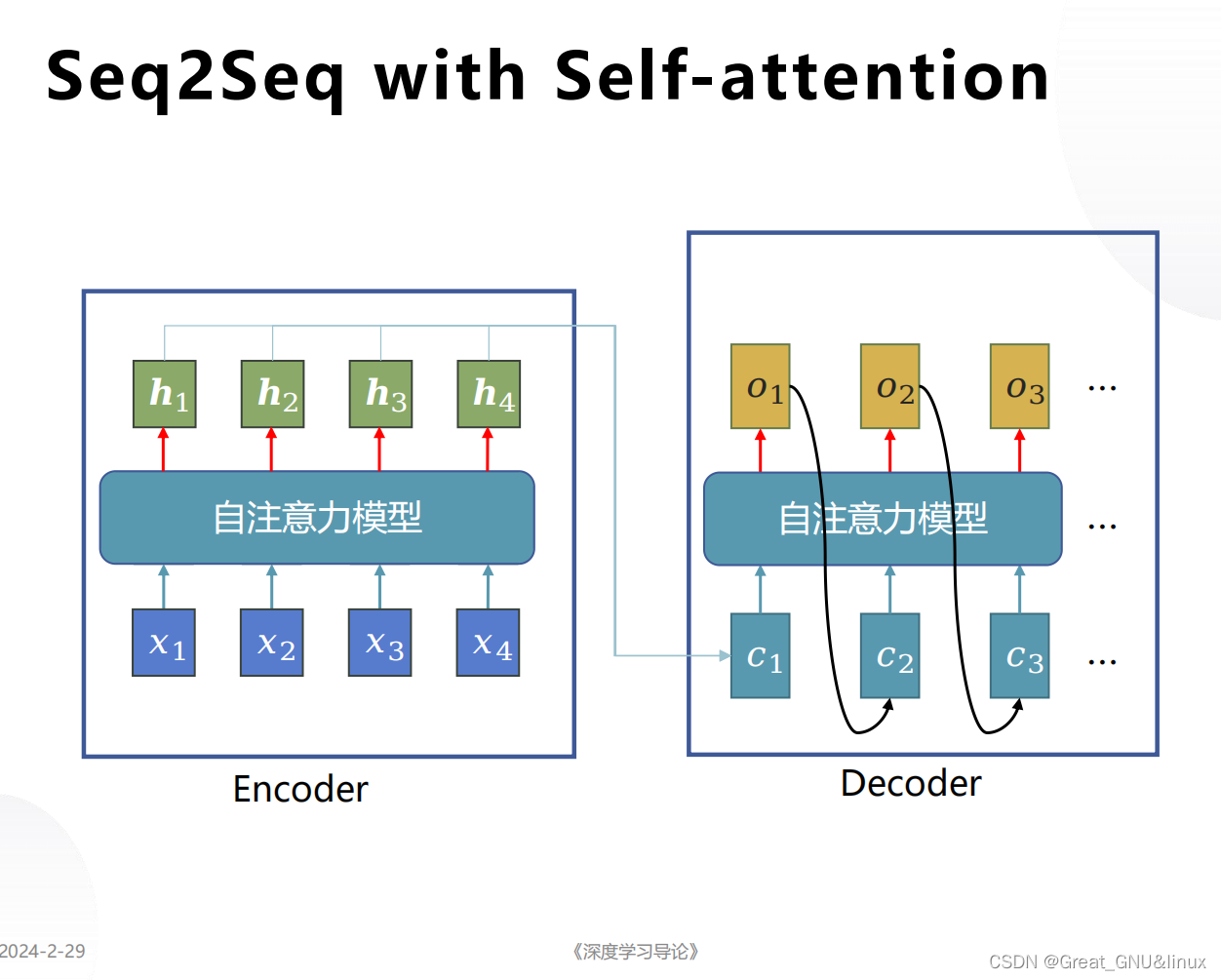
NLP(一)——概述
参考书: 《speech and language processing》《统计自然语言处理》 宗成庆 语言是思维的载体,自然语言处理相比其他信号较为特别 word2vec用到c语言 Question 预训练语言模型和其他模型的区别? 预训练模型是指在大规模数据上进行预训练的模型,通常…...

智慧公厕:打造智慧城市的环卫明珠
在城市建设中,公共卫生设施的完善和智能化一直是重要环节。而智慧公厕作为智慧城市建设的重要组成部分,发挥着不可替代的作用。本文以智慧公厕源头实力厂家广州中期科技有限公司,大量精品案例现场实景实图,解读智慧公厕如何助力打…...
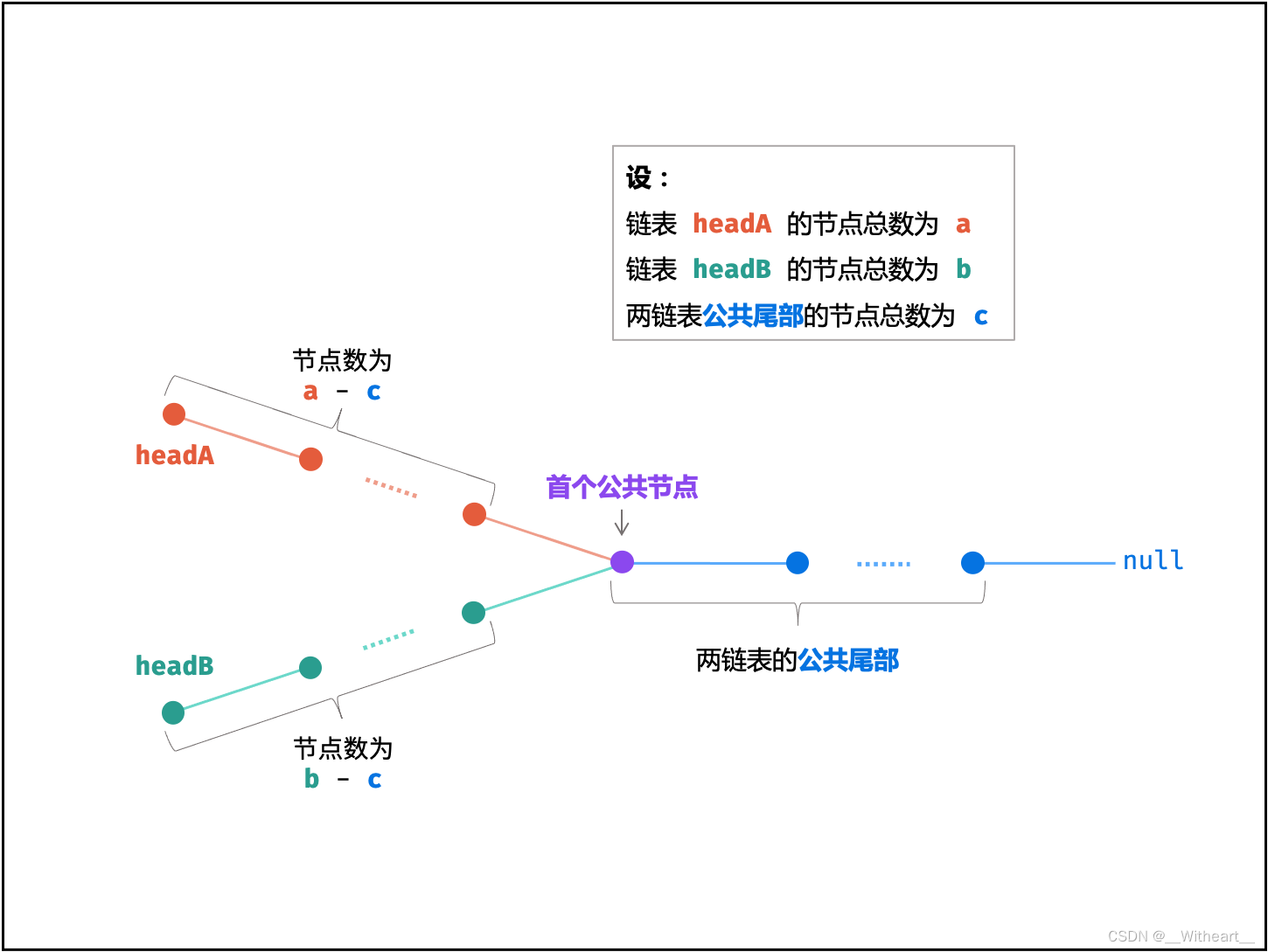
[LeetBook]【学习日记】寻找链表相交节点
来源于「Krahets」的《图解算法数据结构》 https://leetcode.cn/leetbook/detail/illustration-of-algorithm/ 本题与主站 160 题相同:https://leetcode-cn.com/problems/intersection-of-two-linked-lists/ 训练计划 V 某教练同时带教两位学员,分别以…...
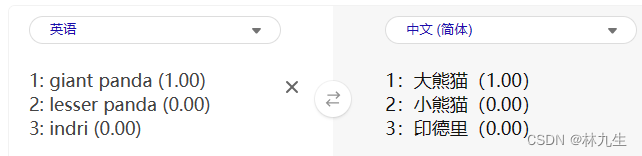
【Python】OpenCV-使用ResNet50进行图像分类
使用ResNet50进行图像分类 如何使用ResNet50模型对图像进行分类。 import os import cv2 import numpy as np from tensorflow.keras.applications.resnet50 import ResNet50, preprocess_input, decode_predictions from tensorflow.keras.preprocessing import image# 设置…...

TypeError: `dumps_kwargs` keyword arguments are no longer supported
TypeError: dumps_kwargs keyword arguments are no longer supported 1. 问题描述2. 解决方法 1. 问题描述 使用 FastChat 启动私有大语言模型,通过一些 UI 工具进行访问时,报以下错误。 略 2024-02-29 09:26:14 | ERROR | stderr | yield f"…...

设计模式学习笔记 - 设计原则 - 3.里氏替换原则,它和多态的区别是什么?
前言 今天来学习 SOLID 中的 L:里氏替换原则。它的英文翻译是 Liskov Substitution Principle,缩写为 LSP。 英文原话是: Functions that use points of references of base classes must be able to use objects of derived classes withou…...
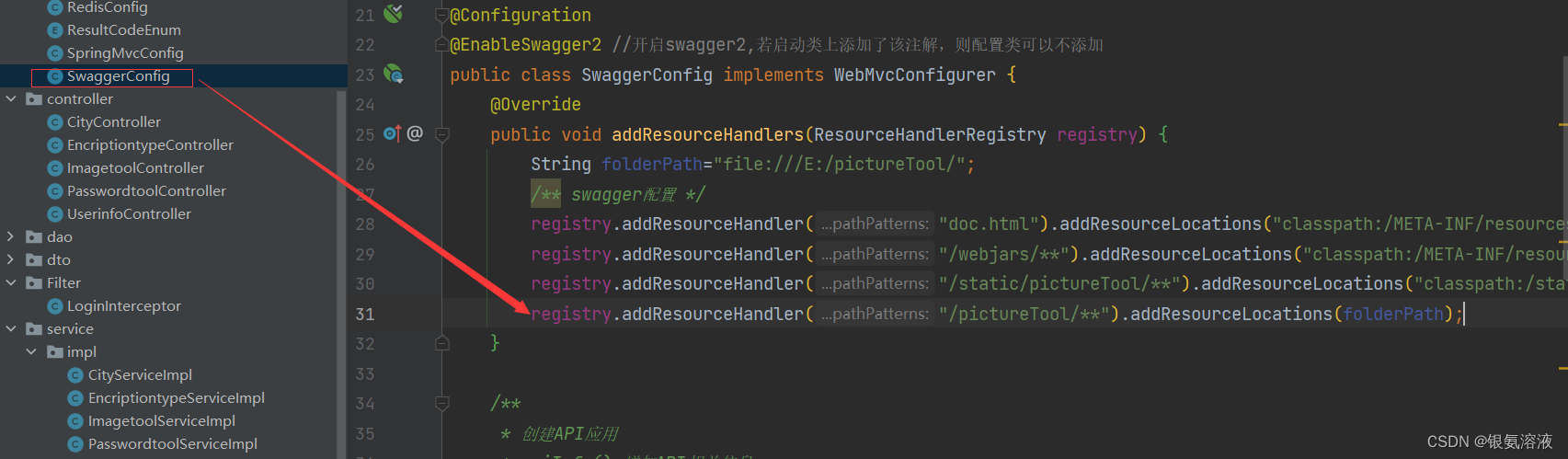
java实现图片转pdf,并通过流的方式进行下载(前后端分离)
首先需要导入相关依赖,由于具体依赖本人也不是记得很清楚了,所以简短的说一下。 iText:PDF 操作库,用于创建和操作 PDF 文件。可通过 Maven 或 Gradle 引入 iText 依赖。 MultipartFile:Spring 框架中处理文件上传的类…...

如何系统的学习Python——Python的基本语法
学习Python的基本语法是入门的第一步,以下是一些常见的基本语法概念: 注释: 用#符号来添加单行注释,或使用三引号(或""")来添加多行注释。 # 这是一个单行注释 这是 多行 注释 变量和数据类型: 变量用…...

相机,棱镜和光场
一、成像方法 Imaging Synthesis Capture 1.Synthesis(图形学上)合成:比如之前学过的光线追踪或者光栅化 2.Capture(捕捉):把真实世界存在的东西捕捉成为照片 二、相机 1.小孔成像 利用小孔成像的相…...
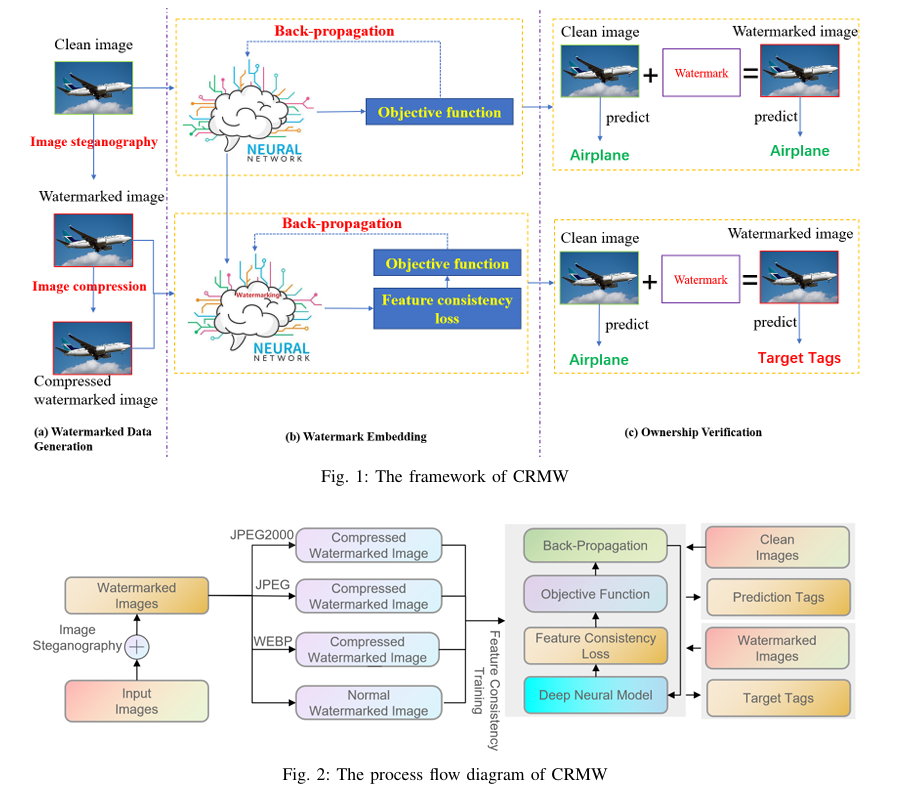
【图像版权】论文阅读:CRMW 图像隐写术+压缩算法
不可见水印 前言背景介绍ai大模型水印生成产物不可见水印CRMW 在保护深度神经网络模型知识产权方面与现有防御机制有何不同?使用图像隐写术和压缩算法为神经网络模型生成水印数据集有哪些优势?特征一致性训练如何发挥作用,将水印数据集嵌入到…...

代码随想录算法训练营第31天—贪心算法05 | ● 435. 无重叠区间 ● *763.划分字母区间 ● *56. 合并区间
435. 无重叠区间 https://programmercarl.com/0435.%E6%97%A0%E9%87%8D%E5%8F%A0%E5%8C%BA%E9%97%B4.html 考点 贪心算法重叠区间 我的思路 先按照区间左坐标进行排序,方便后续处理进行for循环,循环范围是0到倒数第二个元素如果当前区间和下一区间重叠…...

2024《》
vue-cli到哪做了那些事 vue-cli是vue.js的脚手架,用于自动生成vue.jswebpack的项目模板,快速搭建Vue.js项目。 vue cli内置了webpack的一些功能,这些是用webpack打包时需要我们自己配置的,例如: 1.ES6代码转换成ES5代…...

【Web】Java反序列化之从CC3看TemplatesImpl的利用
目录 关于TemplatesImpl 关于TemplatesImpl加载字节码 CC3链分析 纯CC3demo 根据CC3改CC6 关于TemplatesImpl TemplatesImpl 是 Java 中的一个类,通常与 Java 反序列化漏洞相关的攻击中被使用。该类位于 Java 标准库中的 javax.xml.transform 包下。 在 Java…...

【Elasticsearch索引】Recovery恢复索引
文章目录 索引恢复恢复列表获取恢复信息响应详细信息正在进行的恢复响应解析高级设置 本地分片恢复事务日志 索引恢复 索引恢复提供了对正在进行的索引分片恢复的洞察。恢复状态可以针对特定的索引报告,也可以在集群范围内报告。 恢复列表 recovery命令是索引分片…...

如何在 Linux 中快速清空文件而不删除它们?
在Linux系统中,清空文件而不删除它们是一种常见的需求,特别是在需要保留文件结构或权限的情况下。本文将详细介绍如何在Linux环境中快速清空文件内容的多种方法,以及每种方法的优缺点。清空文件通常涉及到文件内容的擦除,但并不涉…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
