蓝桥杯——123
123
二分+等差数列求和+前缀和数组
题目分析

连续一段的和我们想到了前缀和,但是这里的l和r的范围为1e12,明显不能用O(n)的时间复杂度去求前缀和。那么我们开始观察序列的特点,可以按照等差数列对序列进行分块。如上图,在求前10个数的和的时候,我们可以这样求1+3(1+2)+6(1+2+3)+10(1+2+3+4)=20。我们不需要遍历10次就可以求出来。求前缀和代码如下
sum = new long[1500010];
for (int i = 1; i <= 1500000; i++) {t += i;sum[i] = sum[i-1]+t;
}
这里的t最开始等于1,是第一块的数字和,然后等于3,是第二块数字的和,然后等于6是第三块数字的和,以此类推。sum[i]表示的是分块后前i块包含数字的和。
我们可以求出前n块数字的和,那么我们需要知道第l个数字是在哪一块里面,然后求第l个数字是所在块的第几个数字。因为对于最后一块来说,不是所有的数字都会被包含进来,我们要单独对最后一块求数字和。
第一阶段利用二分求第x个数所在的块

图1
如图1所示,我们可以把这个序列分块,第一块有1个数,第二块有2个数,第三块有3个数,第四块有4个数,每一块拥有数的个数是一个等差数列。现在要找到序列中第x个数所在的块数,假设x=3,那么第x个数在第2块中,如果x=4,那么第x个数在第3块中。求第x个数所在的块数,就是求从左往右数,前缀和第一个大于等于x的块。
比如第2块的前缀和就是3,第三块的前缀和就是5。这个可以用二分去求。
int l = 1;int r = 1500000;//最多可以分的块数while(l < r) {int mid = (l + r) / 2;if(sum(mid) < x) {//求mid个块中包含的数字的个数,如果小于x,就是不符合条件,我要向左找l = mid + 1;}else {//符合条件,我要看前面的块是否也是大于等于x的r = mid;}}
这里的sum函数的作用就是求前mid块中包含的数字的个数,因为是等差数列,所以直接用等差数列的求和公式就可以了,sum函数如下
private static long sum(long x) { return (1L + x) * x / 2;
}
第二阶段求前x个数的前缀和
接下来分析二分结束之和我要怎么操作,我要求前x个数字的和。
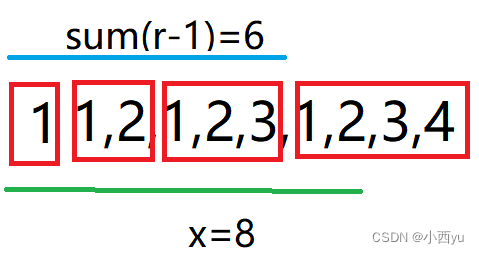
假设x=8,那么第x个数在第4块中,我还要知道,第x个数是第4块中的第几个数字。如图,第4块有4个数,第x个数第4块的第2个数上,那么第2个数是怎么来的呢?就是x-sum(r-1)=8-6=2。其实就是我二分算出来了第x个数在第r块上,那么我只需要把前r-1块包含的数的个数减去就算出来x是在第r块上的第几个数上了。结合上图更好理解。那么前x个数的和就是前r-1块包含数的和加上第r块里面前x-sum(r-1)个数的和。
某一块里面包含的数也是等差数列,求前n个数的和依然可以直接用sum(n)去求。而数组sum[r]里面记录的是前r块包含数字值的前缀和。所以二分结束后的代码是这样子的
private static long f(long x) {int l = 1;int r = 1500000;//最多可以分的块数while(l < r) {int mid = (l + r) / 2;if(sum(mid) < x) {//求mid个块中包含的数字的个数l = mid + 1;}else {r = mid;}}//r--是表示完整的块的个数r--;//就是上文里的r-1//x表示x处在他所在块的第几个位置,需要减去前面所有块包含的数的个数//本来要求x个数字,前r个块中已经包含了sum(r)个数字,第r+1个块x -= sum(r);//前r个块中已经包含了多少个数字return sum[r]+sum(x);
}
还是对于x=8的例子,二分求出来r=4,r–后,r=3,sum[3]=10。x-=sum(3)=8-6=2。sum[3]+sum(2)=10+3=13
注意这道题里对于sum函数的多次应用,但是不是每一次应用含义都是一样的。因为每一块包含的数字个数是等差数列,而每一块内每个数字形成的也是等差数列。
题目代码
import java.util.Scanner;
public class Main {
static long[] sum;
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);long t = 0;//前缀和的预处理sum = new long[1500010];for (int i = 1; i <= 1500000; i++) {t += i;sum[i] = sum[i-1]+t;}int n = scanner.nextInt();while(n-- > 0) {long l = scanner.nextLong();long r = scanner.nextLong();System.out.println(f(r)-f(l-1));//f(r)求的是序列中前r个数的和}
}
//二分 二分求的是x在哪一块中 n*(n-1)/2>l的第一个n
private static long f(long x) {int l = 1;int r = 1500000;//最多可以分的块数while(l < r) {int mid = (l + r) / 2;if(sum(mid) < x) {//求mid个块中包含的数字的个数l = mid + 1;}else {r = mid;}}//r--是表示完整的块的个数r--;//x表示x处在他所在块的第几个位置,需要减去前面所有块包含的数的个数//本来要求x个数字,前r个块中已经包含了sum(r)个数字,第r+1个块x -= sum(r);//前r个块中已经包含了多少个数字return sum[r]+sum(x);
}
//sum函数求前x块包含的数的个数,同时也可以表示某一个块中,前x个数的总和
private static long sum(long x) {// TODO Auto-generated method stub return (1L + x) * x / 2;
}
}
相关文章:
蓝桥杯——123
123 二分等差数列求和前缀和数组 题目分析 连续一段的和我们想到了前缀和,但是这里的l和r的范围为1e12,明显不能用O(n)的时间复杂度去求前缀和。那么我们开始观察序列的特点,可以按照等差数列对序列进行分块。如上图,在求前10个…...
嵌入式基础知识-信号量,PV原语与前趋图
本篇来介绍信号量与PV原语的一些知识,并介绍其在前趋图上的应用分析。本篇的知识属于操作系统部分的通用知识,在嵌入式软件开发中,同样会用到这些知识。 1 信号量 信号量是最早出现的用来解决进程同步与互斥问题的机制(可以把信…...

代码遗产:探索祖传代码的历史、挑战与现代融合艺术
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua,在这里我会分享我的知识和经验。&#x…...
Vue3:用vite创建Vue3项目
一、简介 vite是新一代前端构建工具,官网地址:https://vitejs.cn vite的优势如下: 轻量快速的热重载(HMR),能实现极速的服务启动。对 TypeScript、JSX、CSS 等支持开箱即用。真正的按需编译,不…...
STM32 (2)
1.stm32编程模型 将C语言程序烧录到芯片中会存储在单片机的flsah存储器中,给芯片上电后,Flash中的程序会逐条进入到CPU中去执行,进而CPU去控制各种模块(即外设)去实现各种功能。 2.寄存器和寄存器编程 CPU通过控制其…...

docker部署nginx+反向代理配置/代理宿主机网段服务器
1、安装docker,并运行 2、拉取nginx镜像 docker pull nginx3、运行nginx容器,将文件拷贝至本地,并将nginx容器删除 #运行nginx容器 docker run -id --name mynginx -p 8080:80 nginx#将配置文件从容器内拷贝至本地 docker cp 容器ID:/et…...
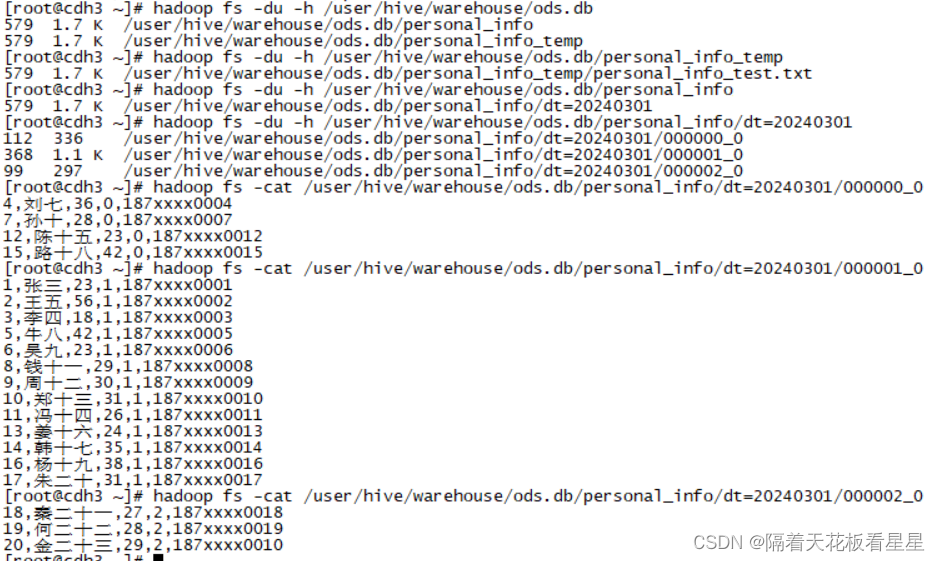
初识Hive
官网地址为: Design - Apache Hive - Apache Software Foundation 一、架构 先来看下官网给的图: 图上显示了Hive的主要组件及其与Hadoop的交互。Hive的主要组件有: UI: 用户向系统提交查询和其他操作的用户界面。截至2011年&…...
Google发布Genie硬杠Sora:通过大量无监督视频训练最终生成可交互虚拟世界
前言 Sora 问世才不到两个星期,谷歌的世界模型也来了,能力看似更强大:它生成的虚拟世界自主可控 第一部分 首个基础世界模型Genie 1.1 Genie是什么 Genie是第一个以无监督方式从未标记的互联网视频中训练的生成式交互环境(the first gener…...
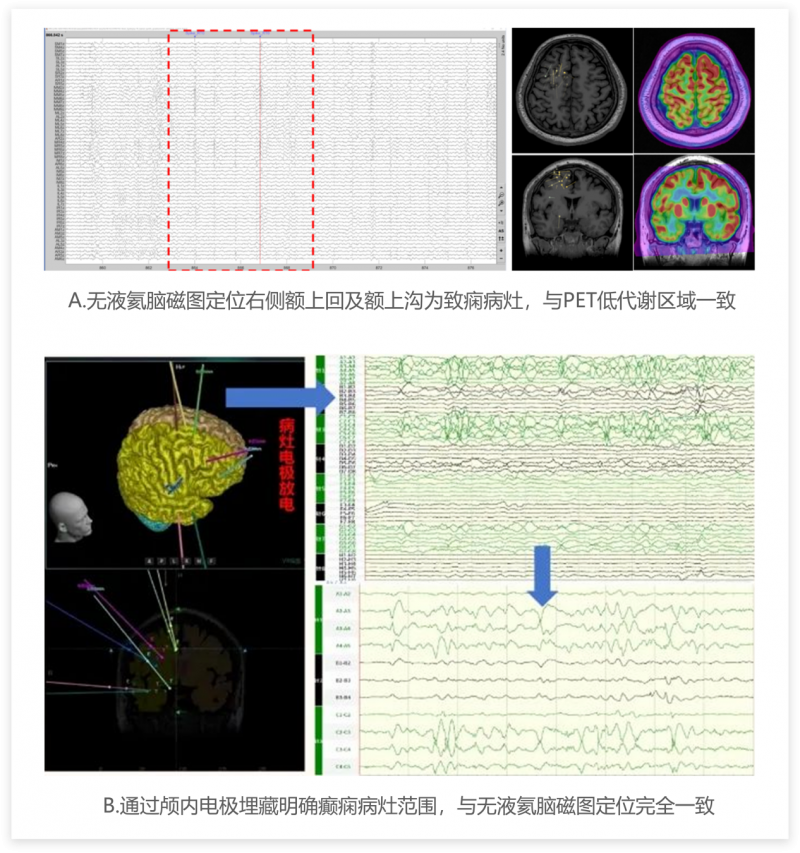
全球首台!未磁科技256通道无液氦脑磁图仪及芯片化原子磁力计正式发布
2024年2月3日,由北京未磁科技有限公司牵头的国家重点研发计划诊疗装备与生物医用材料重点专项“新型无液氦脑磁图系统研发”项目2023年度总结会暨2024年推进会顺利召开。会上发布了项目取得的重大成果——全球首台256通道无液氦脑磁图仪Marvel MEG Pro。此项重磅成果…...
配置)
openssl3.2 - exp - 内存操作(建立,写入,读取)配置
文章目录 openssl3.2 - exp - 内存操作(建立,写入,读取)配置概述笔记调试细节运行效果测试工程实现main.cppCMyOsslConfig.hCMyOsslConfig.cppEND openssl3.2 - exp - 内存操作(建立,写入,读取)配置 概述 我的应用的配置文件是落地加密的, 无法直接用openssl配置接口载入读取…...

前端食堂技术周刊第 114 期:Interop 2024、TS 5.4 RC、2 月登陆浏览器的新功能、JSR、AI SDK 3.0
美味值:🌟🌟🌟🌟🌟 口味:凉拌鸡架 食堂技术周刊仓库地址:https://github.com/Geekhyt/weekly 大家好,我是童欧巴。欢迎来到前端食堂技术周刊,我们先来看下…...
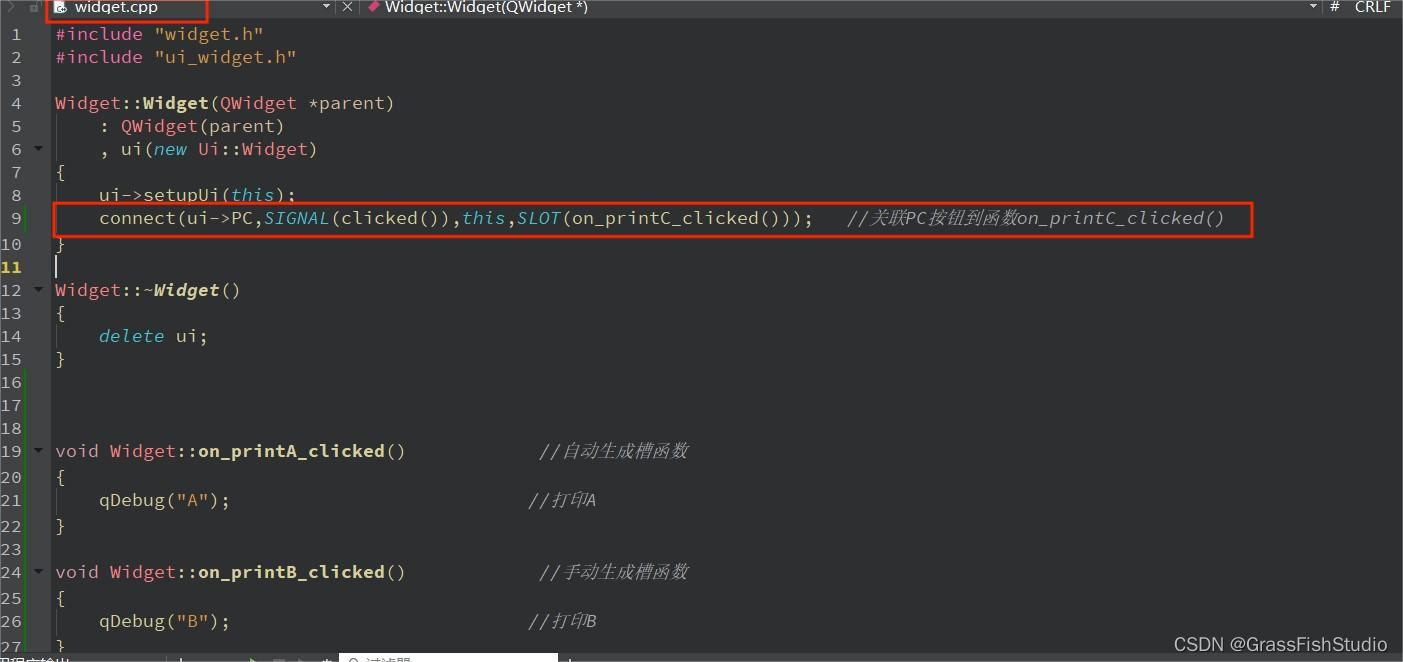
#QT(信号与槽)
1.IDE:QTCreator 2.实验:自动添加槽函数,手动添加槽函数 3.记录 (1)自动添加 a.拖拽widget.ui,放置push-button组件,并且自动生成槽函数 b.发现widget.cpp和widget.h中出现添加的槽函数,注意w…...

go 设置滚动日志
方案 通过 log/slog 实现结构化日志生成,这是go1.21中推出的新特性;通过 lumberjack 实现日志文件分割。 示例 package mainimport ("gopkg.in/natefinch/lumberjack.v2""log/slog""os""path/filepath" )fun…...

Rollup入门学习:前端开发的构建利器
在前端开发领域,构建工具对于优化项目结构和提升代码效率扮演着至关重要的角色。Rollup作为一款轻量级且功能强大的JavaScript模块打包器,近年来备受开发者青睐。本文将带你走进Rollup的世界,帮助你快速入门并掌握其核心用法。 一、Rollup简介…...
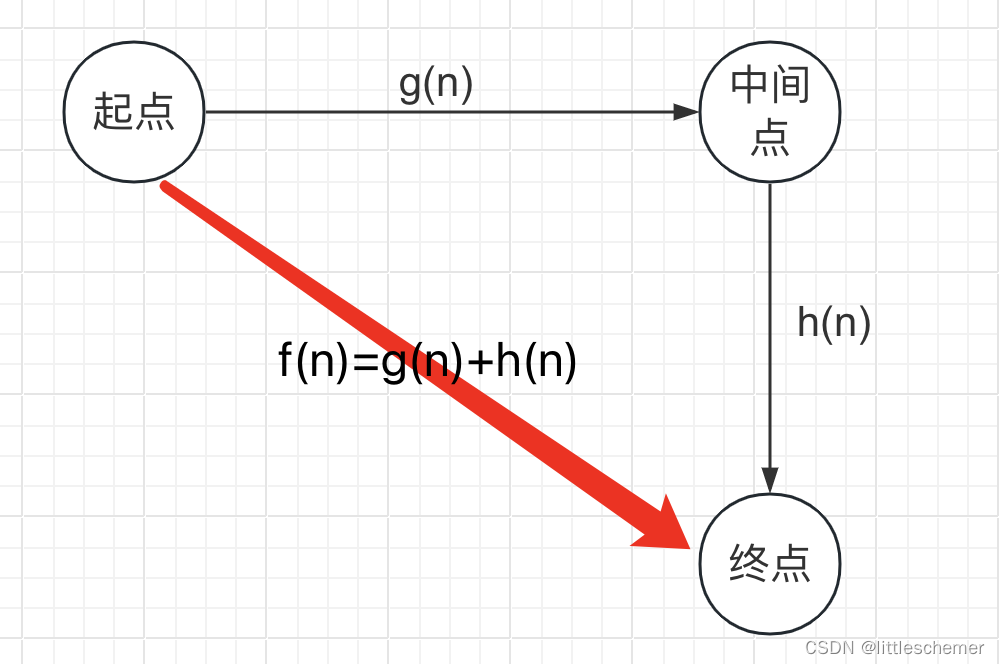
游戏寻路之A*算法(GUI演示)
一、A*算法介绍 A*算法是一种路径搜索算法,用于在图形网络中找到最短路径。它结合了Dijkstra算法和启发式搜索的思想,通过综合利用已知的最短路径和估计的最短路径来优化搜索过程。在游戏自动寻路得到广泛应用。 二、A*算法的基本思想 在图形网络中选择一个起点和终点。维护…...

软件工程顶会——ICSE '24 论文清单、摘要
1、A Comprehensive Study of Learning-based Android Malware Detectors under Challenging Environments 近年来,学习型Android恶意软件检测器不断增多。这些检测器可以分为三种类型:基于字符串、基于图像和基于图形。它们大多在理想情况下取得了良好的…...

Vue点击复制到剪切板
一、Vue2写法 安装 (官网地址) npm install --save vue-clipboard2 使用 //main.js import VueClipboard from vue-clipboard2 Vue.use(VueClipboard)//页面使用 <button type"button"v-clipboard:copy"message"v-clipboard:su…...
链路负载均衡之DNS透明代理
一、DNS透明代理 一般来说,企业的客户端上都只能配置一个运营商的DNS服务器地址,DNS服务器通常会将域名解析成自己所在ISP内的Web服务器地址,这将导致内网用户的上网流量都集中在一个ISP的链路上转发,最终可能会造成链路拥塞&…...

2024大语言模型LLM基础|语义搜索Semantic_Search全解
目录 语义搜索Semantic_Search代码详解 为甚麽用Pinecone做向量索引?优点是什么? 有哪些常见向量索引方法? Pinecone做向量索引怎么用? 向量索引全解:含原理解析: 语义搜索Semantic_Search代码详解 1…...

vue中使用echarts实现人体动态图
最近一直处于开发大屏的项目,在开发中遇到了一个小知识点,在大屏中如何实现人体动态图。然后看了下echarts官方文档,根据文档中的示例调整出来自己想要的效果。 根据文档上发现 series 中 type 类型设置为 象形柱形图,象形柱图是…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
