C#插入排序算法
插入排序实现原理
插入排序算法是一种简单、直观的排序算法,其原理是将一个待排序的元素逐个地插入到已经排好序的部分中。
具体实现步骤如下
-
首先咱们假设数组长度为n,从第二个元素开始,将当前元素存储在临时变量temp中。
-
从当前元素的前一个位置开始向前遍历,比较temp与每个已排序元素的值大小。
-
如果已排序元素大于临时变量temp中的元素,则将该元素后移一位,继续向前比较。
-
直到找到小于或等于temp的元素位置,将temp插入到该位置后面。
-
这样重复步骤2至4,直到所有元素都被插入到适当的位置则排序结束。
插入排序完整代码示例
public static void InsertionSort(int[] array){int arrayLength = array.Length;//数组长度(时间复杂度为O(n^2))for (int i = 1; i < arrayLength; ++i){//定义临时变量int temp = array[i];int j = i - 1;while (j >= 0 && array[j] > temp){array[j + 1] = array[j];j--;}array[j + 1] = temp;}}public static void InsertionSortRun(){int[] array = { 26, 15, 5, 3, 38, 36, 44, 27, 47, 2, 46, 4, 50, 19, 48 };Console.WriteLine("排序前:" + string.Join(", ", array));InsertionSort(array);Console.WriteLine("排序后:" + string.Join(", ", array));}
输出结果

总结
插入排序算法是一种简单且直观的排序算法。它的时间复杂度为O(n^2),其中n是待排序数组的长度。插入排序在处理小型数据集时具有一定优势,但是对于大型数据集,插入排序的性能会较差。
参考文章
https://blog.csdn.net/weixin_44231544/article/details/126278933
相关文章:

C#插入排序算法
插入排序实现原理 插入排序算法是一种简单、直观的排序算法,其原理是将一个待排序的元素逐个地插入到已经排好序的部分中。 具体实现步骤如下 首先咱们假设数组长度为n,从第二个元素开始,将当前元素存储在临时变量temp中。 从当前元素的前一…...
快速搭建Vue前端框架
快速搭建Vue前端框架 安装Vue Vue官方安装过程:https://cli.vuejs.org/zh/guide/installation.html 二.创建Vue工程 2.2 安装淘宝镜像 安装淘宝镜像(会让你安装Vue的速度加快): npm config set registry https://registry.npm.taobao.or…...

TS中private和protected的区别
在 TypeScript 中,private 和 protected 是两种访问修饰符,用于限制类成员(如属性、方法等)的可见性和可访问性。它们的主要区别在于访问权限的宽松程度。 1. private 当一个类的成员被标记为 private 时,它只能在该…...

虚拟机Hyper-V操作记录
问题1:安装Hyper-V,虚拟机监控程序无法打钩,提示该固件的虚拟化支持被禁用 主板型号:华硕ASUS ROG STRIX Z390-E GAMING 解决方法:进入BIOS,Advanced/CPU Configuration/Intel(VMX) Virtualization Technol…...
)
90. 子集 II(力扣LeetCode)
文章目录 90. 子集 II题目描述回溯算法 90. 子集 II 题目描述 给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。 解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 …...

202435读书笔记|《半小时漫画中国史》——读点经济学与历史,生活更美好,趣味烧脑土地制度、商鞅变法、华丽丽的丝绸之路这里都有
202435读书笔记|《半小时漫画中国史》——读点经济学与历史,生活更美好,趣味烧脑土地制度、商鞅变法、华丽丽的丝绸之路这里都有 1. 土地政策、度量衡及税收2. 商鞅变法3. 西汉经济4. 西汉盐铁大辩论5. 西汉丝绸之路 《半小时漫画中国史:经济…...

2023下半年主品牌锋芒依旧,江南布衣打破既定天花板?
在过去的2023年里,服装板块令人意外的领涨消费大盘,国家统计局数据显示,上半年服装零售额同比增长12.8%,远超商品零售大盘的增速6.8%。 整体表现强劲的同时,“局部”表现是否也尽如人意。近日,作为时尚服装…...
Gitlab: PHP项目CI/CD实践
目录 1 说明 2 CI/CD 2.1 部署方式一:增量部署 2.1.1 目标服务器准备 2.2.2 Gitlab及Envoy脚本 2.2 部署方式二:镜像构建与部署 2.2.1 推送到私有化容器仓库 准备工作 脚本 要点 2.2.2 推送到hub.docker.com 准备工作 脚本 3 参考&#x…...
c语言游戏实战(10):坤坤的篮球回避秀
前言: 这款简易版的球球大作战是博主耗时两天半完成的,玩家需要控制坤坤在游戏界面上移动,来躲避游戏界面上方不断掉下来的篮球。本游戏使用C语言和easyx图形库编写,旨在帮助初学者了解游戏开发的基本概念和技巧。 在开始编写代…...
初学arp欺骗
首先准备一台靶机这里用虚拟机的win10 已知网关与ip地址(怕误伤) 现在返回kali从头开始 首先探测自己的网关 然后扫内网存活的ip 发现有3台 用nmap扫一下是哪几台 成功发现我们虚拟机的ip 现在虚拟机可以正常访问网络 接下来直接开梭 ip网关 返回虚拟机…...

ftp几个常见错误问题及解决办法
1、无法上传网页,FTP故障-提示“无法连接服务器”错误。 问题出现原因:FTP客户端程序设置问题,客户上网线路问题,ftp服务器端问题。 处理方法:建议客户使用CUTPFTP软件来上传客户的网页,在“F…...
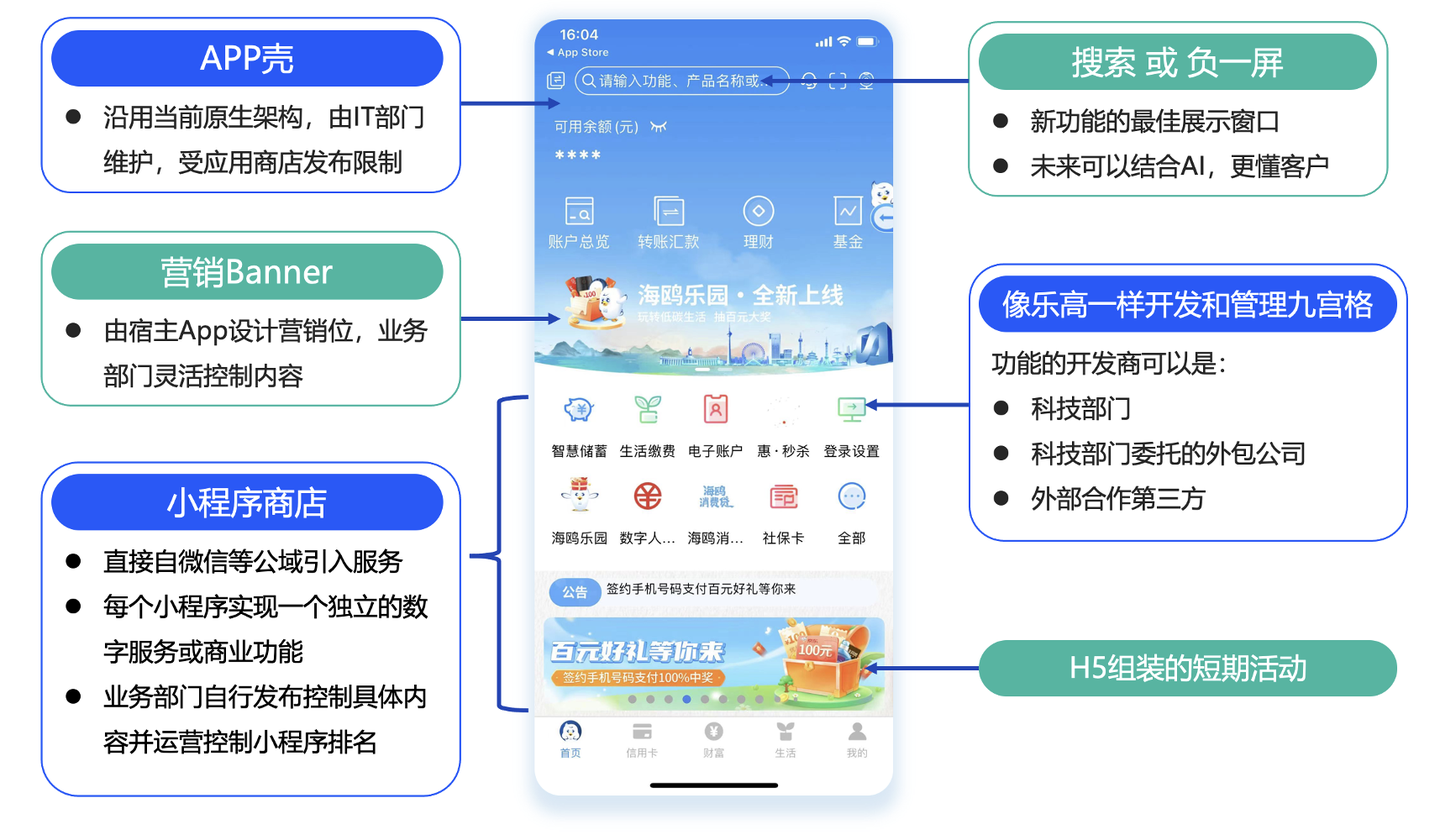
鸿蒙App开发新思路:小程序转App
国家与国家之间错综复杂,在谷歌的安卓操作系统“断供”后,鸿蒙系统的市场化&独立化的道路便显而易见了。 2024年1月18日,华为宣布,不再兼容安卓的“纯血鸿蒙”--HarmonyOS NEXT鸿蒙星河版最终面世,并与2024年Q4正…...
)
C++17之std::invoke: 使用和原理探究(全)
C进阶专栏:http://t.csdnimg.cn/5mV9r 目录 1.概述 2.辅助类 3.原理分析 4.总结 1.概述 在之前的 C 版本中,要调用不同类型的可调用对象,需要使用不同的语法,例如使用函数调用运算符 () 来调用函数或函数指针,使用…...
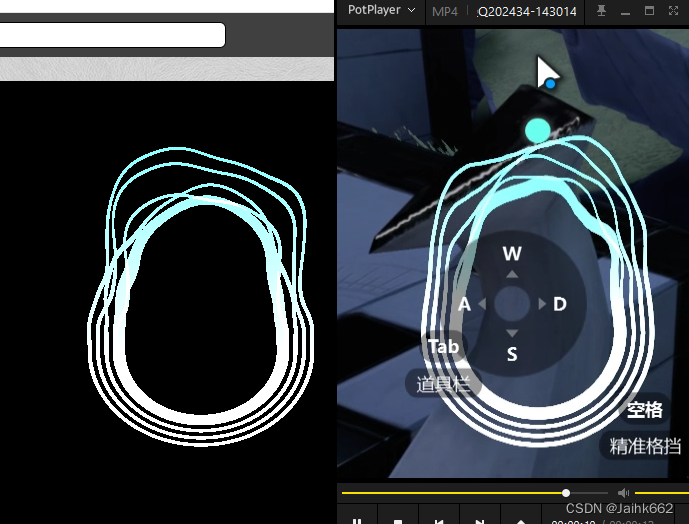
shadertoy 游戏《来自星尘》摇杆复刻
正确的做法应该是上 noise 而不是叠加 sin 波,不过如果不想麻烦的话叠波还是一个不错的选择:整体效果如下,已经非常形似 直接上链接:Shader - Shadertoy BETA float radiusScale 0.9; float variation(vec2 v1, vec2 v2, float …...
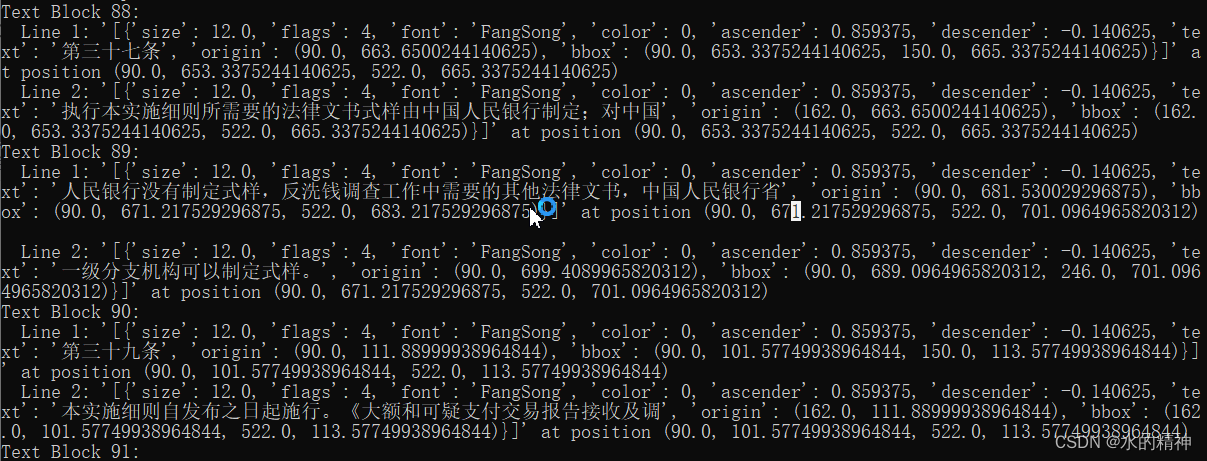
获取PDF中的布局信息——如何获取段落
PDF解析是极其复杂的问题。不可能靠一个工具解决全部问题,尤其是五花八门,格式不统一的PDF文件。除非有钞能力。如果没有那就看看可以分为哪些问题。 提取文本内容,提取表格内容,提取图片。我认为这些应该是分开做的事情。python有…...

Laya2.13.3在Web条件下使用键盘控制相机移动
需求:在Laya开发时,常常没法移动相机来观察场内的环境,故制作一个移动相机的脚本来是实现此功能,目前先使用键盘后续会添加鼠标控制移动旋转等功能。 onEnable(){this.camera new Laya.Camera(0, 0.1, 100);this._tempVector3 n…...

centos系统服务器在Jenkins执行playwright UI自动化测试框架
centos系统服务器在Jenkins执行playwright UI自动化测试框架 1. centos7.9系统中安装playwright环境报错 playwright/driver/node: /lib64/libc.so.6: version `GLIBC_2.25 not found经过查找资料,playwright 仅支持Ubuntu系统,其他的Linux服务器系统不支持,为此采用docke…...

boost.redis崩溃的解决方法
使用boost.redis的协程一定要co_spawn在strand对象中。 正确的用法: boost::asio::co_spawn(boost::dasio::make_strand(ioc),XXXCoroutine(),boost::asio::detached ); 错误的用法: boost::asio::co_spawn(ioc,XXXCoroutine(),boost::asio::detache…...
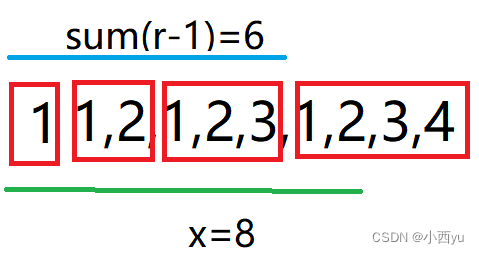
蓝桥杯——123
123 二分等差数列求和前缀和数组 题目分析 连续一段的和我们想到了前缀和,但是这里的l和r的范围为1e12,明显不能用O(n)的时间复杂度去求前缀和。那么我们开始观察序列的特点,可以按照等差数列对序列进行分块。如上图,在求前10个…...
嵌入式基础知识-信号量,PV原语与前趋图
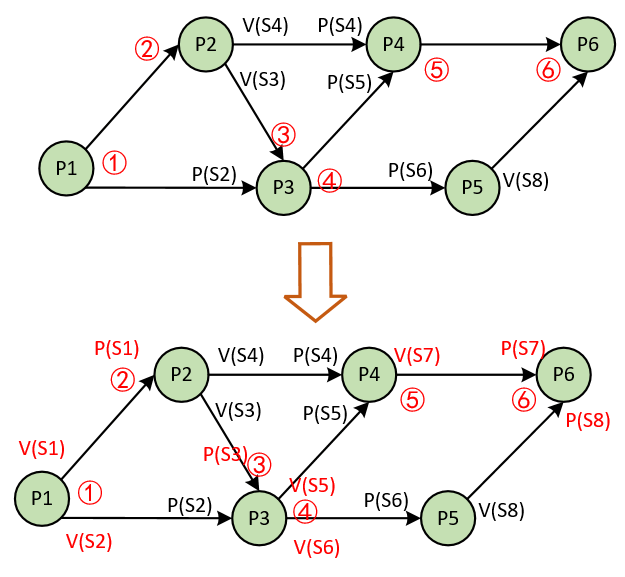
本篇来介绍信号量与PV原语的一些知识,并介绍其在前趋图上的应用分析。本篇的知识属于操作系统部分的通用知识,在嵌入式软件开发中,同样会用到这些知识。 1 信号量 信号量是最早出现的用来解决进程同步与互斥问题的机制(可以把信…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...
