当前位置： 首页 > news >正文

「滚雪球学Java」：JDBC(章节汇总)

news 2026/2/9 22:39:55

在这里插入图片描述

🏆本文收录于「滚雪球学Java」专栏，专业攻坚指数级提升，助你一臂之力，带你早日登顶🚀，欢迎大家关注&&收藏！持续更新中，up！up！up！！

环境说明：Windows 10 + IntelliJ IDEA 2021.3.2 + Jdk 1.8

文章目录

    • 附录源码
  • ☀️建议/推荐你
  • 📣关于我

  …
  好啦，这期的内容就基本接近尾声啦，若你想学习更多，可以参考这篇专栏总结《「滚雪球学Java」教程导航帖》，本专栏致力打造最硬核 Java 零基础系列学习内容，🚀打造全网精品硬核专栏，带你直线超车；欢迎大家订阅持续学习。

附录源码

  如上涉及所有源码均已上传同步在「Gitee」，提供给同学们一对一参考学习，辅助你更迅速的掌握。

☀️建议/推荐你

  无论你是计算机专业的学生，还是对编程有兴趣的小伙伴，都建议直接毫无顾忌的学习此专栏「滚雪球学Java」，bug菌郑重承诺，凡是学习此专栏的同学，均能获取到所需的知识和技能，全网最快速入门Java编程，就像滚雪球一样，越滚越大，指数级提升。

  最后，如果这篇文章对你有所帮助，帮忙给作者来个一键三连，关注、点赞、收藏，您的支持就是我坚持写作最大的动力。

  同时欢迎大家关注公众号:「猿圈奇妙屋」 ，以便学习更多同类型的技术文章，免费白嫖最新BAT互联网公司面试题、4000G pdf电子书籍、简历模板、技术文章Markdown文档等海量资料。

📣关于我

  我是bug菌，CSDN | 掘金 | infoQ | 51CTO 等社区博客专家，历届博客之星Top30，掘金年度人气作者Top40，51CTO年度博主Top12，华为云 | 阿里云| 腾讯云等社区优质创作者，全网粉丝合计15w+ ；硬核微信公众号「猿圈奇妙屋」，欢迎你的加入！免费白嫖最新BAT互联网公司面试题、4000G pdf电子书籍、简历模板等海量资料。

相关文章：

「滚雪球学Java」：JDBC(章节汇总)

🏆本文收录于「滚雪球学Java」专栏，专业攻坚指数级提升，助你一臂之力，带你早日登顶🚀，欢迎大家关注&&收藏！持续更新中，up！up！up！&#xf…...

编程日记 2024/3/5 11:15:08

RT-DETR改进RepVGG结构：简单但功能强大的卷积神经网络架构

💡本篇内容：RT-DETR改进RepVGG结构：简单但功能强大的卷积神经网络架构 💡🚀🚀🚀本博客 改进源代码改进 适用于 RT-DETR 按步骤操作运行改进后的代码即可 💡本文提出改进 原创 方式：二次创新，RT-DETR专属 应部分读者要求，新增一篇RepVGG 论文理论部分 + 原…...

编程日记 2024/3/5 11:14:06

C#进阶高级语法之LINQ ：Lambda 表达式

C# 中的 LINQ (Language Integrated Query) 提供了一种声明性的数据查询和操作方法，它允许开发人员对集合、数据库等数据源进行查询和操作，而不需要编写复杂的循环和手动编码。Lambda 表达式与 LINQ 紧密相关，它提供了一种简洁的方式来定义匿…...

编程日记 2024/3/5 11:11:03

react hook: useCallback

useCallback的主要使用场景在于优化性能，并确保当传递回调函数给子组件时，子组件不会因为父组件的重渲染而重新创建函数。 使用场景 1.当你需要将回调函数传递给子组件时，使用useCallback可以确保子组件在重新渲染时不会不必要地重新创建函数…...

编程日记 2024/3/5 11:05:57

java面试（jvm）

JVM内存模型 细分Eden： java类加载过程？双亲委派机制？一个对象从加载到JVM，再到被GC清除过程？ JAVA类加载器：AppClassLoader - ExtClassLoader - BootStrapClassLoader。每种类加载器都有他自己的加载目录…...

编程日记 2024/3/5 11:03:55

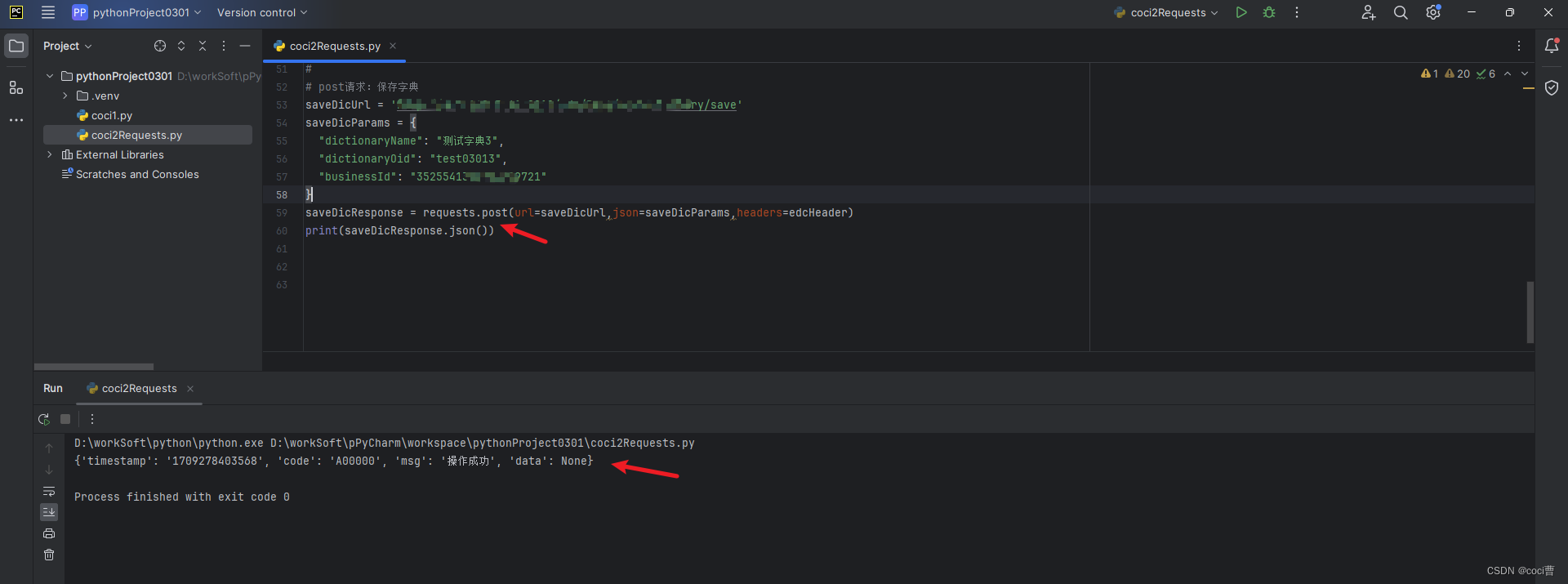
自动化测试摸索：python+selenium+pytest(持续更新.....)

一、环境搭建 1、python 安装 下载链接：Python Releases for Windows | Python.org 自己选择合适的版本下载 当下载完毕时，找到该安装程序：python-3.12.2-amd64.exe文件，双击启动安装向导。 为了防止C:盘文件因系统故障或者无…...

编程日记 2024/3/5 11:01:53

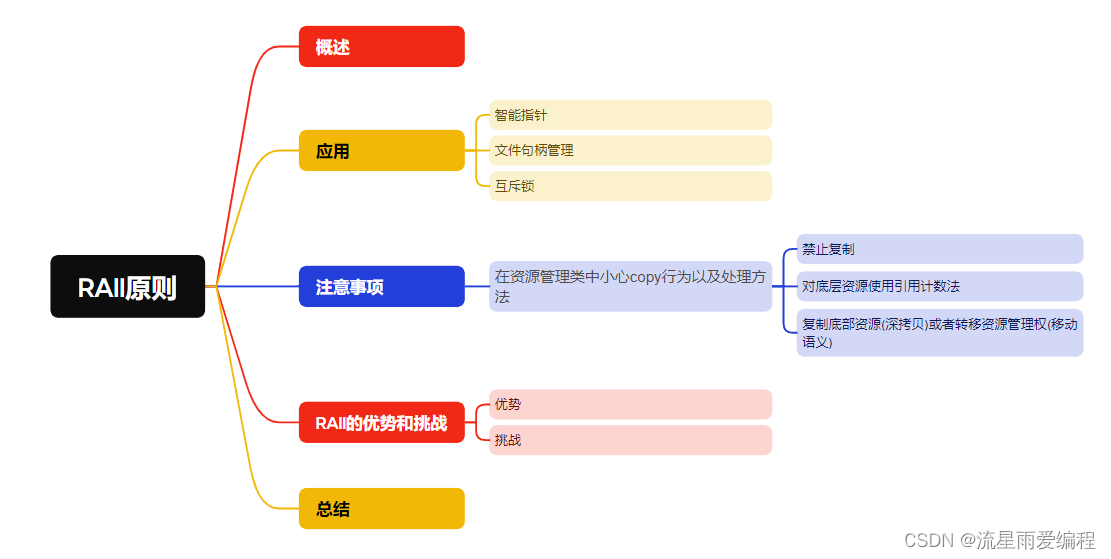
C++惯用法之RAII思想: 资源管理

C编程技巧专栏：http://t.csdnimg.cn/eolY7 目录 1.概述 2.RAII的应用 2.1.智能指针 2.2.文件句柄管理 2.3.互斥锁 3.注意事项 3.1.禁止复制 3.2.对底层资源使用引用计数法 3.3.复制底部资源(深拷贝)或者转移资源管理权(移动语义) 4.RAII的优势和挑战 5.总…...

编程日记 2024/3/5 11:00:52

矢量图是什么，有哪些格式的文件

矢量图是一种图形设计中常用的图像类型，与我们日常见到的光栅图像（如JPEG、PNG等）有本质的区别。矢量图基于数学方程和几何元素（如点、线、曲线和形状）来表示图像，而不是像光栅图那样通过像素阵列来表示。这…...

编程日记 2024/3/5 10:57:48

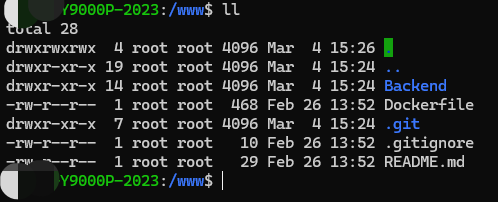
Linux 设置快捷命令

以ll命令为例： 在 Linux 系统上，ll 命令通常不是一个独立的程序，而是 ls 命令的一个别名。 这个别名通常在用户的 shell 配置文件中定义，比如 .bashrc 或 .bash_aliases 文件中。 要在 Debian 上启用 ll 命令，你可以按…...

编程日记 2024/3/5 10:53:44

SpringCloudFeign远程调用

文章目录 1. Feign 是什么2. Feign 的使用2.1 引入依赖2.2 写接口2.3 服务调用方2.4 启动测试 3. Feign 日志配置4. Feign 使用优化5. 注意包扫描问题 1. Feign 是什么 Feign 是一个声明式、模板化的 HTTP 客户端，它是由 Netflix 开发并开源的。Feign 极大地简化了…...

编程日记 2024/3/5 10:52:38

Java中List、Set、Map三种集合之间的区别

Java中List、Set、Map三种集合之间的区别 1. List2. Set3. Map 在Java中，List、Set和Map是三种常见的集合类型，它们之间也有一些重要的区别： 1. List List是有序集合，可以存储重复元素。List的实现类常见有ArrayList、LinkedLis…...

编程日记 2024/3/5 10:50:35

SpringMVC之DispatcherServlet组件

目录 一、SpringMVC的核心处理流程二、DispatcherServlet1、init()方法2、doDispatch()方法3、AbstractAnnotationConfigDispatcherServletInitializer类 一、SpringMVC的核心处理流程 请求到达 DispatcherServlet DispatcherServlet 的请求处理： DispatcherServlet…...

编程日记 2024/3/5 10:47:32

抢商家、夺用户、比低价，抖音、快手、小红书“奇招尽出”

随着流量红利逐渐消退，国内电商平台之间互相内卷已成为了行业常态，而无论是在该领域深耕已久的淘宝、京东、拼多多等电商巨头，还是新跨界而来的抖音、快手、小红书等电商新秀都在不断地进行创新，以便为商家提供更好的服务&#xf…...

编程日记 2024/3/5 10:45:29

ChatGPT引领的AI面试攻略系列：AI全栈工程师篇

系列文章目录 AI全栈工程师（本文） 文章目录 系列文章目录一、前言二、面试题1. 基础理论与数据处理2. 机器学习3. 深度学习4. 大模型与迁移学习5. 计算机视觉6. 自然语言处理（NLP）7. 多模态学习8. AI生成内容（AIGC&am…...

编程日记 2024/3/5 10:44:28

上位机图像处理和嵌入式模块部署（qmacvisual配置）

【 声明：版权所有，欢迎转载，请勿用于商业用途。 联系信箱：feixiaoxing 163.com】 前面我们谈到了qmacvisual的编译、验证码、用户登录以及流程的编辑，这部分都是基础工作。事实上，除了这些内容之外&#xf…...

编程日记 2024/3/5 10:35:19

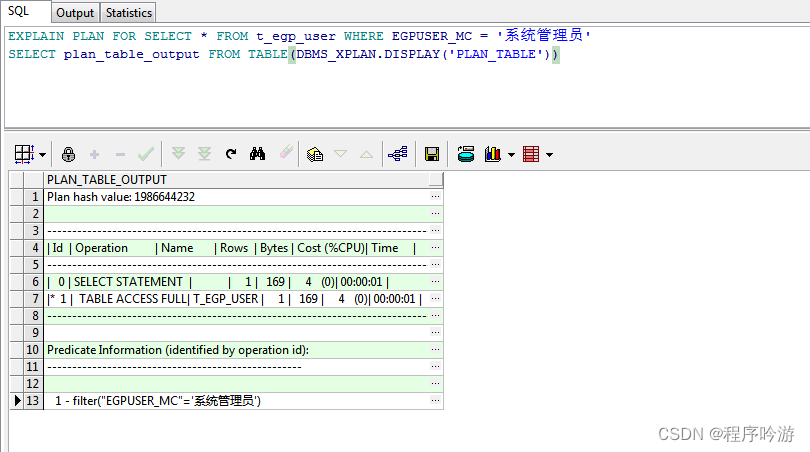
EXPLAIN PLAN FOR：在Oracle中生成执行计划

目录 案例 解析 Operation类型 在Oracle中，可以使用 EXPLAIN PLAN FOR 命令来生成执行计划，然后通过 SELECT plan_table_output FROM TABLE(DBMS_XPLAN.DISPLAY(PLAN_TABLE))来查看执行计划。需要注意的是，这两个命令需要在同一个窗口下运…...

编程日记 2024/3/5 10:34:18

蓝桥杯 9241.飞机降落

这道题本来作者以为是可以用一些小技巧进行暴力解法的&#xff0c;但是后来试了一下&#xff0c;不能过去全部数据。 下面是对半个的题解&#xff1a; #include<iostream> #include<stdio.h> #include<cstring> #include<cstdlib> #include<cmath…...

编程日记 2024/3/5 10:28:12

数据可视化原理-腾讯-散点图

在做数据分析类的产品功能设计时&#xff0c;经常用到可视化方式&#xff0c;挖掘数据价值&#xff0c;表达数据的内在规律与特征展示给客户。 可是作为一个产品经理&#xff0c;&#xff08;1&#xff09;如果不能够掌握各类可视化图形的含义&#xff0c;就不知道哪类数据该用…...

编程日记 2024/3/5 10:26:09

深度学习-Pytorch实现经典AlexNet网络：山高我为峰

深度学习-Pytorch实现经典AlexNet网络之山高我为峰 深度学习中&#xff0c;经典网络引领一波又一波的技术革命&#xff0c;从LetNet到当前最火的GPT所用的Transformer&#xff0c;它们把AI技术不断推向高潮。2012年AlexNet大放异彩&#xff0c;它把深度学习技术引领第一个高峰…...

编程日记 2024/3/5 10:25:08

25考研习题记录

3月 汤家凤《1800》 基础篇 日期高等数学线性代数概率论3.1 P92-93 P212-214 3.4 P10-15 P10-19 极限题62题 P73-74 P170-172 行列式17题 考研竞赛凯哥每日一题 张宇高数30讲页数3.4P74...

编程日记 2024/3/5 10:21:03

工业安全零事故的智能守护者：一体化AI智能安防平台

前言&#xff1a; 通过AI视觉技术&#xff0c;为船厂提供全面的安全监控解决方案&#xff0c;涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面&#xff0c;能够实现对应负责人反馈机制&#xff0c;并最终实现数据的统计报表。提升船厂…...

编程新知 2026/1/21 9:20:07

Swift 协议扩展精进之路：解决 CoreData 托管实体子类的类型不匹配问题（下）

概述 在 Swift 开发语言中&#xff0c;各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过&#xff0c;在涉及到多个子类派生于基类进行多态模拟的场景下&#xff0c;…...

编程新知 2026/1/23 4:56:05

【算法训练营Day07】字符串part1

文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接&#xff1a;344. 反转字符串 双指针法&#xff0c;两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

编程新知 2025/8/27 14:38:58

spring：实例工厂方法获取bean

spring处理使用静态工厂方法获取bean实例&#xff0c;也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下&#xff1a; 定义实例工厂类&#xff08;Java代码&#xff09;&#xff0c;定义实例工厂&#xff08;xml&#xff09;&#xff0c;定义调用实例工厂&#xff…...

编程新知 2025/11/25 22:46:30

Reasoning over Uncertain Text by Generative Large Language Models

https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达，从日常对话到特定领域的文档（例如医学文档）（Heritage 2013；Landmark、Gulbrandsen 和 Svenevei…...

编程新知 2026/2/8 2:27:29

技术栈RabbitMq的介绍和使用

目录 1. 什么是消息队列&#xff1f;2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

编程新知 2026/1/23 10:10:53

Netty从入门到进阶（二）

二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架&#xff0c;用于…...

编程新知 2026/1/26 5:44:16

【无标题】路径问题的革命性重构：基于二维拓扑收缩色动力学模型的零点隧穿理论

路径问题的革命性重构&#xff1a;基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中&#xff08;图1&#xff09;&#xff1a; mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

编程新知 2025/10/21 1:07:59

DiscuzX3.5发帖json api

参考文章&#xff1a;PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下&#xff0c;适配我自己的需求 有一个站点存在多个采集站&#xff0c;我想通过主站拿标题&#xff0c;采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

编程新知 2025/11/25 17:20:50

​​企业大模型服务合规指南：深度解析备案与登记制度​​

伴随AI技术的爆炸式发展&#xff0c;尤其是大模型&#xff08;LLM&#xff09;在各行各业的深度应用和整合&#xff0c;企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者&#xff0c;还是积极拥抱AI转型的传统企业&#xff0c;在面向公众…...

编程新知 2026/2/9 1:32:22