【LeetCode】第 387 场周赛
3069. 将元素分配到两个数组中 I
给你一个下标从 1 开始、包含 不同 整数的数组 nums ,数组长度为 n 。
你需要通过 n 次操作,将 nums 中的所有元素分配到两个数组 arr1 和 arr2 中。在第一次操作中,将 nums[1] 追加到 arr1 。在第二次操作中,将 nums[2] 追加到 arr2 。之后,在第 i 次操作中:
如果 arr1 的最后一个元素 大于 arr2 的最后一个元素,就将 nums[i] 追加到 arr1 。否则,将 nums[i] 追加到 arr2 。
通过连接数组 arr1 和 arr2 形成数组 result 。例如,如果 arr1 == [1,2,3] 且 arr2 == [4,5,6] ,那么 result = [1,2,3,4,5,6] 。
返回数组 result 。
复杂度:O(N)
class Solution {public int[] resultArray(int[] nums) {int n = nums.length;List<Integer> l1 = new ArrayList();List<Integer> l2 = new ArrayList();l1.add(nums[0]);l2.add(nums[1]);for(int i=2; i<n; i++) {int i1 = l1.size()-1;int i2 = l2.size()-1;if(l1.get(i1) > l2.get(i2)) {l1.add(nums[i]);} else {l2.add(nums[i]);}}int[] res = new int[n];int idx = 0;for(int i=0; i<l1.size(); i++) {res[idx] = l1.get(i);idx ++;}for(int i=0; i<l2.size(); i++) {res[idx] = l2.get(i);idx ++;}return res;}
}
3070. 元素和小于等于 k 的子矩阵的数目
给你一个下标从 0 开始的整数矩阵 grid 和一个整数 k。
返回包含 grid 左上角元素、元素和小于或等于 k 的 子矩阵 的
数目
。
思路:二维数组前缀和
复杂度:O(N*N)
class Solution {public int countSubmatrices(int[][] grid, int k) {int m = grid.length;int n = grid[0].length;int[][] dp = new int[m][n];// dp[0][0] = grid[0][0];int ans = 0;for(int i=0; i<m; i++) {int s = 0;for(int j=0; j<n; j++) {s = s + grid[i][j];dp[i][j] = s;if(i-1>=0) {dp[i][j] += dp[i-1][j];}if(dp[i][j] <= k) {ans ++;}}}return ans;}
}
3071. 在矩阵上写出字母 Y 所需的最少操作次数
给你一个下标从 0 开始、大小为 n x n 的矩阵 grid ,其中 n 为奇数,且 grid[r][c] 的值为 0 、1 或 2 。
如果一个单元格属于以下三条线中的任一一条,我们就认为它是字母 Y 的一部分:
从左上角单元格开始到矩阵中心单元格结束的对角线。
从右上角单元格开始到矩阵中心单元格结束的对角线。
从中心单元格开始到矩阵底部边界结束的垂直线。
当且仅当满足以下全部条件时,可以判定矩阵上写有字母 Y :
属于 Y 的所有单元格的值相等。
不属于 Y 的所有单元格的值相等。
属于 Y 的单元格的值与不属于Y的单元格的值不同。
每次操作你可以将任意单元格的值改变为 0 、1 或 2 。返回在矩阵上写出字母 Y 所需的 最少 操作次数。
思路:数组y记录Y内区域每种元素出现次数,数组ny记录Y外区域每种元素出现次数。则所求问题即为求nn-y[i]-ny[j]的最小值,其中i与j不相等。
复杂度:O(NN)
class Solution {public int minimumOperationsToWriteY(int[][] grid) {int n = grid.length;int[] y = new int[3];int[] ny = new int[3];boolean[][] vis = new boolean[n][n];for(int i=0; i<=n/2; i++) {vis[i][i] = true;}int idx = n/2;for(int j=n/2; j<n; j++) {vis[idx][j] = true;idx --;}idx = n/2;for(int i=n/2; i<n; i++) vis[i][idx]=true;for(int i=0; i<n; i++) {for(int j=0; j<n; j++) {if(vis[i][j]) {y[grid[i][j]] ++;} else {ny[grid[i][j]] ++;}}}// for(int i=0; i<n; i++) {// for(int j=0; j<n; j++) {// System.out.print(vis[i][j] +" ");// }// System.out.println(" ");// }
// // for(int j=0; j<3; j++) {// System.out.print(y[j] +" ");// }int ans = n*n;for(int i=0; i<3; i++) {for(int j=0; j<3; j++) {if(i!=j){// System.out.println(n*n-y[i]+ny[j]);ans = Math.min(ans, n*n-y[i]-ny[j]);} }}return ans;}
}
3072. 将元素分配到两个数组中 II
现定义函数 greaterCount ,使得 greaterCount(arr, val) 返回数组 arr 中 严格大于 val 的元素数量。
你需要使用 n 次操作,将 nums 的所有元素分配到两个数组 arr1 和 arr2 中。在第一次操作中,将 nums[1] 追加到 arr1 。在第二次操作中,将 nums[2] 追加到 arr2 。之后,在第 i 次操作中:
如果 greaterCount(arr1, nums[i]) > greaterCount(arr2, nums[i]) ,将 nums[i] 追加到 arr1 。
如果 greaterCount(arr1, nums[i]) < greaterCount(arr2, nums[i]) ,将 nums[i] 追加到 arr2 。
如果 greaterCount(arr1, nums[i]) == greaterCount(arr2, nums[i]) ,将 nums[i] 追加到元素数量较少的数组中。
如果仍然相等,那么将 nums[i] 追加到 arr1 。
连接数组 arr1 和 arr2 形成数组 result 。例如,如果 arr1 == [1,2,3] 且 arr2 == [4,5,6] ,那么 result = [1,2,3,4,5,6] 。
返回整数数组 result 。
思路:树型数组。先将数组排序,用排序后的数组的序号来缩小数据范围。树型数组的[1,i]表示小于等于i的数量,则gc=n-sum[1,i]
复杂度:O(NlogN)
class Fenwick {public final int[] tree;public Fenwick(int n) {tree = new int[n];}public void add(int idx) {while(idx<tree.length) {tree[idx] ++;idx += idx & -idx;}}public int sum(int i) {int res =0;while(i>0) {res += tree[i];i -= i& -i;}return res;}
}class Solution {public int[] resultArray(int[] nums) {int[] sorted = nums.clone();Arrays.sort(sorted);int n = nums.length;Fenwick ta = new Fenwick(n+1);Fenwick tb = new Fenwick(n+1);List<Integer> a = new ArrayList();List<Integer> b = new ArrayList();a.add(nums[0]);b.add(nums[1]);ta.add(Arrays.binarySearch(sorted, nums[0])+1);tb.add(Arrays.binarySearch(sorted, nums[1])+1);for(int i=2; i<n; i++) {// 找到对应的映射int v1 = Arrays.binarySearch(sorted, nums[i]) +1;int gc1 = a.size() - ta.sum(v1);int gc2 = b.size() - tb.sum(v1);if(gc1>gc2 || gc1==gc2 && a.size()<=b.size()) {a.add(nums[i]);ta.add(v1);} else {b.add(nums[i]);tb.add(v1);}}for(int num:b) {a.add(num); }int[] res = new int[n];for(int i=0; i<n; i++) {res[i] = a.get(i);}return res;}
}
相关文章:

【LeetCode】第 387 场周赛
3069. 将元素分配到两个数组中 I 给你一个下标从 1 开始、包含 不同 整数的数组 nums ,数组长度为 n 。 你需要通过 n 次操作,将 nums 中的所有元素分配到两个数组 arr1 和 arr2 中。在第一次操作中,将 nums[1] 追加到 arr1 。在第二次操作…...
基于 Vue3打造前台+中台通用提效解决方案(下)
47、通用组件 - 倒计时组件 特惠部分存在一个倒计时的功能,所以我们需要先处理对应的倒计时模块,并把它处理成一个通用组件。 那么对于倒计时模块我们又应该如何进行处理呢? 所谓倒计时,其实更多的是一个时间的处理,那么对于时间的处理,此时我们就需要使用到一个第三方…...
Topaz Video AI:一键提升视频品质,智能重塑影像魅力 mac/win版
Topaz Video AI是一款革命性的视频智能处理软件,它利用先进的机器学习和人工智能技术,为视频创作者提供了前所未有的视频增强和修复功能。无论您是专业视频编辑师、摄影师,还是热爱视频创作的爱好者,Topaz Video AI都能帮助您轻松…...

高效办公软件中哪个提醒待办事项更有效
在忙碌的办公环境中,每个人都像是一台精密运转的机器,处理着各种任务和待办事项。而在这其中,总有一些人,他们仿佛拥有超能力般,总是能准时、高效地完成每一项工作。他们的秘密武器是什么呢?答案就是——高…...
牛客练习赛122
D:圆 正着求删除的最小代价不好做,采用逆向思维,求选择一些不相交的线段使得构成一个圆的代价尽量大,最后答案就是所有线段权值之和减去最大代价。 那么如何求这个最大代价呢?显然区间DP 老套路:破环成链࿰…...
软考复习调整策略和学习计划!
根据软考办发布的最新通知,在群里引起了热烈讨论的是2024年度计算机技术与软件专业技术资格(水平)考试的安排。其中,信息系统项目管理师(简称高项)的考试次数从每年两次减少到只有5月份进行,而系…...

1小时网络安全事件报告要求,持安零信任如何帮助用户应急响应?
12月8日,国家网信办起草发布了《网络安全事件报告管理办法(征求意见稿)》(以下简称“办法”)。拟规定运营者在发生网络安全事件时应当及时启动应急预案进行处置。 1小时报告 按照《网络安全事件分级指南》,…...

mysql使用连接池
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、mysql连接池?二、使用步骤1.引入库 前言 提示:这里可以添加本文要记录的大概内容: 例如: 提示:…...

06. Nginx进阶-Nginx代理服务
proxy代理功能 正向代理 什么是正向代理? 正向代理(forward proxy),一个位于客户端和原始服务器之间的服务器。 工作原理 为了从原始服务器获取内容,客户端向代理发送一个请求并指定目标(即原始服务器…...

STM32 (1)
1.基本信息 stm32是由ST公司生产的一种32位微控制器(单片机)。 1.1 各种型号 stm32是32位单片机的总称,有多种不同的系列。 32即用32个比特位表示一个地址,寻址范围:0x00000000 --0xffffffff (4GB) 1.2 存储密度 …...
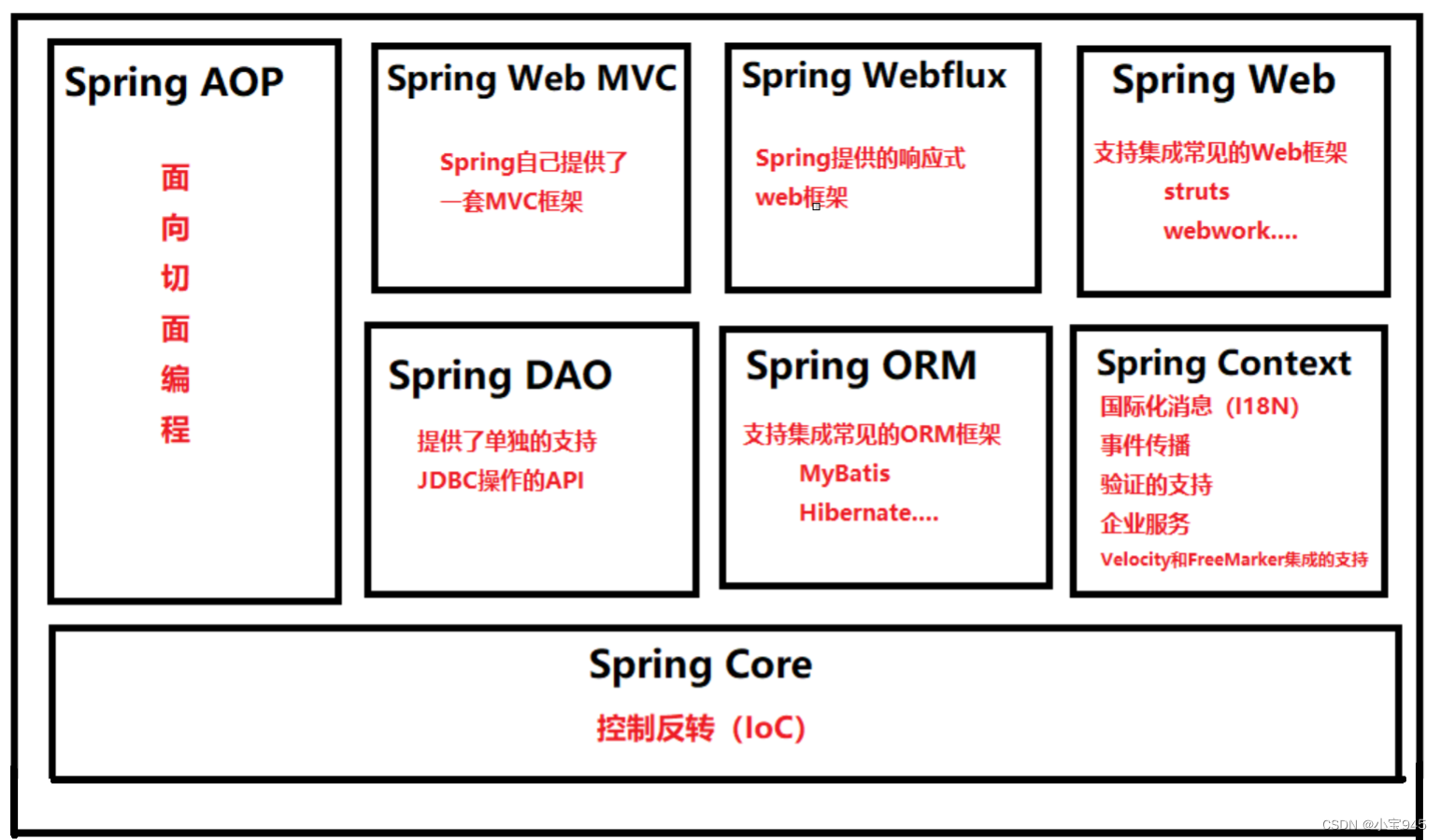
Spring初始(相关基础知识和概述)
Spring初始(相关基础知识和概述) 一、Spring相关基础知识(引入Spring)1.开闭原则OCP2.依赖倒置原则DIP3.控制反转IoC 二、Spring概述1.Spring 8大模块2.Spring特点2.Spring的常用jar文件 一、Spring相关基础知识(引入S…...

【Swift 周报 第四十七期
文章目录 前言新闻和社区苹果财报来袭:营收有望再创新高 巴克莱或将惨遭打脸?Apple 为在全球范围内提供迷你 App 和游戏访问的流媒体游戏服务和 App 发布新选项Swift Student Challenge 将于 2 月 5 日开放申请 提案通过的提案正在审查的提案 Swift论坛推…...

STM32(16)使用串口向电脑发送数据
发送字节 发送数组 发送字符和字符串 字符: 字符串: 字符串在电脑中以字符数组的形式存储...

利用大模型技术进行测试用例推荐如何实现
利用大模型技术进行测试用例推荐,可以通过以下步骤实现: 确定目标和需求:明确测试用例推荐的目标和需求,例如推荐哪些类型的测试用例、推荐的数量、推荐的准确率等。 收集数据:收集历史测试用例、需求文档、设计文档等…...
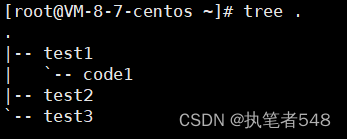
Linux学习:初识Linux
目录 1. 引子:1.1 简述:操作系统1.2 学习工具 2. Linux操作系统中的一些基础概念与指令2.1 简单指令2.2 ls指令与文件2.3 cd指令与目录2.4 文件目录的新建与删除指令2.5 补充指令1:2.6 文件编辑与拷贝剪切2.7 文件的查看2.8 时间相关指令2.9 …...

Python CGI编程错误汇总
文章目录 1 前言2 测试文件3 问题总结 1 前言 在学习Python CGI编程时,运行起来总是有各种各样的问题,故将问题进行总结,以便新接触Python的童鞋能少走弯路 以下均为本人遇到对应报错的解决方案,可能存在其他问题但报错相同的情况…...

第十三届蓝桥杯大赛软件赛省赛C/C++ 大学 B 组 统计子矩阵
#include<iostream> #include<algorithm> #include<cstring> #include<string> #include<vector> #include<queue>using namespace std;int cnt,temp; int n,m,K; int a[505][505]; int pre[505][505];//二维前缀和void sol() {cin>>…...
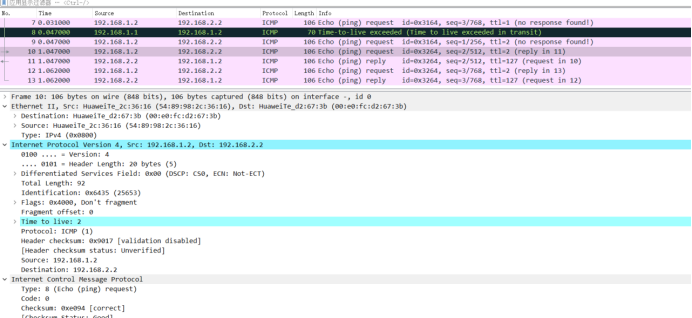
计算机网络实验 基于ENSP的协议分析
实验二 基于eNSP的协议分析 一、实验目的: 1)熟悉VRP的基本操作命令 2)掌握ARP协议的基本工作原理 3)掌握IP协议的基本工作原理 4)掌握ICMP协议的基本工作原理 二、实验内容: 1、场景1:两台PC机…...

Java实现手机库存管理
一、实验任务 编写一个程序,模拟库存管理系统。该系统主要包括系统首页、商品入库、商品显示和删除商品功能。每个功能的具体要求如下: 1.系统的首页:用于显示系统所有的操作,并且可以选择使用某一个功能。 2.商品入库功能&…...
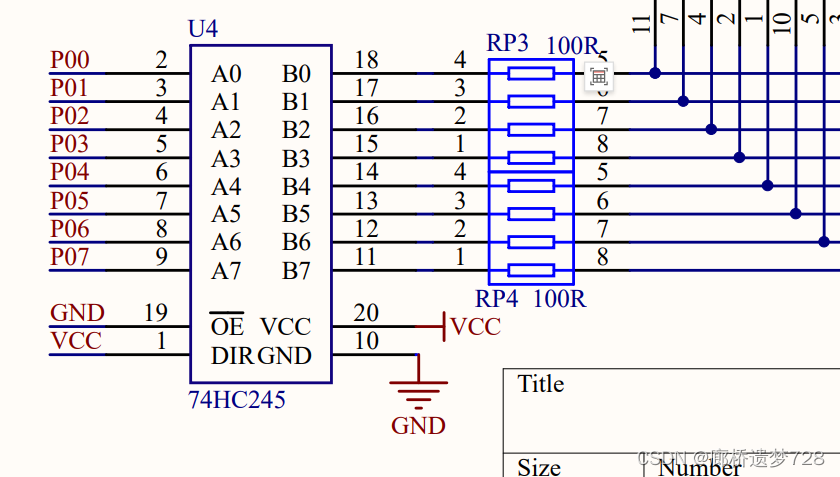
单片机入门:LED数码管
LED数码管 LED数码管:由多个发光二极管封装在一起组成的“8”字型的器件。如下图所示: 数码管引脚定义 一位数码管 内部由八个LED组成。器件有十个引脚。 对于数码管内的8个LED有共阴和共阳两种连接方法。 共阴:将8个LED的阴极都连接到一…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
