UnityShader——09数学知识3
方阵
行与列数量相等的矩阵,n*n阶矩阵
对角矩阵
当对角线以外的矩阵内元素全为0,则称之为对角矩阵,对角矩阵的前提是必须是方阵
单位矩阵
对角线元素全为1,其余元素全为0,属于对角矩阵的一部分
矩阵和向量
把1 * n阶矩阵称为行向量,n * 1阶矩阵称为列向量
当向量与矩阵进行运算的时候需要确定是行向量还是列向量
矩阵的转置
[ 1 2 3 4 5 6 7 8 9 ] T \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix} ^T 147258369 T = [ 1 4 7 2 5 8 3 6 9 ] \begin{bmatrix} 1 & 4 & 7\\ 2 & 5 & 8\\ 3 & 6 & 9 \end{bmatrix} 123456789
即行变为列,列变为行
矩阵转置的转置是其本身
对角矩阵的转置是其本身
标量与矩阵的乘法
以三阶矩阵为例:
kM = k [ m 11 m 12 m 13 m 21 m 22 m 23 m 31 m 32 m 33 ] \begin{bmatrix} m_{11} & m_{12} & m_{13}\\ m_{21} & m_{22} & m_{23}\\ m_{31} & m_{32} & m_{33} \end{bmatrix} m11m21m31m12m22m32m13m23m33 = [ k m 11 k m 12 k m 13 k m 21 k m 22 k m 23 k m 31 k m 32 k m 33 ] \begin{bmatrix} km_{11} & km_{12} & km_{13}\\ km_{21} & km_{22} & km_{23}\\ km_{31} & km_{32} & km_{33} \end{bmatrix} km11km21km31km12km22km32km13km23km33
矩阵的乘法
相乘的条件:前一个矩阵的列等于下一个矩阵的行

矩阵乘法特点

向量矩阵相乘

DX中是行向量
OpenGL中是列向量
相关文章:

UnityShader——09数学知识3
方阵 行与列数量相等的矩阵,n*n阶矩阵 对角矩阵 当对角线以外的矩阵内元素全为0,则称之为对角矩阵,对角矩阵的前提是必须是方阵 单位矩阵 对角线元素全为1,其余元素全为0,属于对角矩阵的一部分 矩阵和向量 把1 * n阶矩阵称…...

langchain学习笔记(九)
RunnableBranch: Dynamically route logic based on input | 🦜️🔗 Langchain 基于输入的动态路由逻辑,通过上一步的输出选择下一步操作,允许创建非确定性链。路由保证路由间的结构和连贯。 有以下两种方法执行路由 1、通过Ru…...
周处除三害在线资源最新电影1080p高清
打开下面这个链接就可以看到 周处除三害在线资源最新电影1080p高清 如果链接打不开,就复制下面的网址到浏览器打开 https://www.zhufaka.cn/liebiao/A09504AE3BF8BD06 用阿里云盘下载,下载完成之后,用迅雷播放 周处除三害在线资源最新电…...

STM32CubeIDE基础学习-新建STM32CubeIDE基础工程
STM32CubeIDE基础学习-新建STM32CubeIDE基础工程 前言 有开发过程序的朋友都清楚,后面开发是不需要再新建工程的,一般都是在初学时或者有特殊需要的时候才需要新建项目工程的。 后面开发都是可以在这种已有的工程上添加相关功能就行,只要前…...

R语言简介|你对R语言了解多少?
R语言是一种专门用于统计计算和图形展示的开源编程语言,它在数据科学领域有着广泛的应用。下面对R语言的环境、基础语法及注释进行解释: R语言环境 安装与配置 安装R语言通常可以从官方站点下载对应操作系统的安装包,如Windows、Linux、ma…...
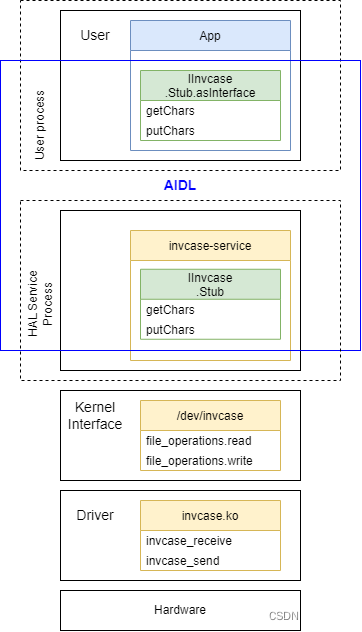
Android的硬件接口HAL
我一直觉得,现代计算机不是一门科学,起码快算不上一门理科科学。上上下下全是人造,左左右右全是生意,用管理学,经济学去学计算机,也许更看得懂很多问题。HAL就是一个典型例子。 传统Linux绕开了微软的霸权…...

【js】数组的常用方法
增加 push,unshift,splice,concat 前面三种修改原数组,concat不会修改原数组push 从后面添加数据,并返回新数组的长度unshift 从前面添加数据,并返回新数组的长度splice 可以接受三个参数,第一个参数开始位置,第二个参数是删除元素的数量,第三个参数是插入的数据concat 合并数…...
08. Nginx进阶-Nginx动静分离
简介 什么是动静分离? 通过中间件将动态请求和静态请求进行分离。分离资源,减少不必要的请求消耗,减少请求延时。 动静分离的好处 动静分离以后,即使动态服务不可用,静态资源仍不受影响。 动静分离示意图 动静分离…...

RPC--一起学习吧之架构
RPC(远程过程调用)是一种网络通信协议,它允许一台计算机(客户端)上的程序调用另一台计算机(服务器)上的程序,就像调用本地程序一样。RPC 可以使得网络中的不同进程能够相互调用&…...
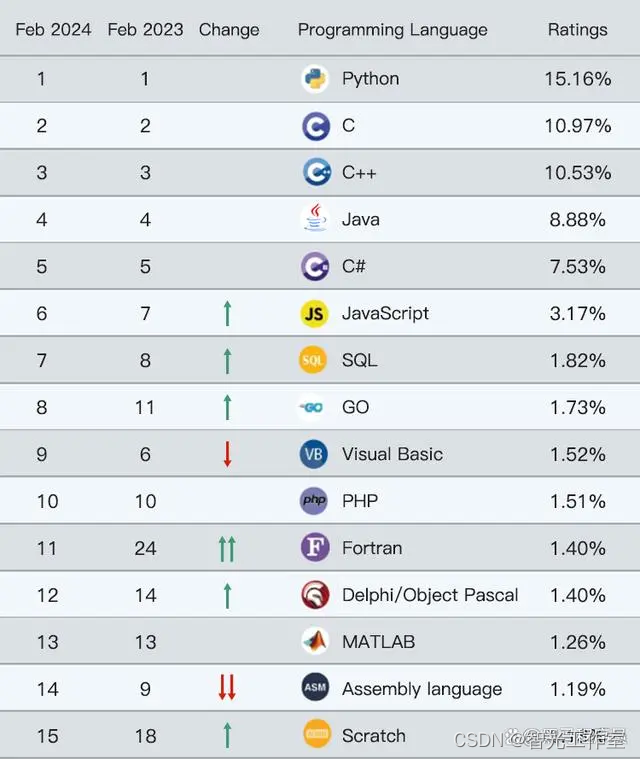
服务器后端是学习java还是php
没有绝对的"最好"语言,每种后端语言都有其适用的场景和特点。以下是几种常用的后端语言: 1. Java:Java是一种通用且强大的语言,广泛用于企业级应用和大型系统。它有很好的性能和可靠性,并且具有优秀的生态系…...

DCFL: for Oriented Tiny Object Detection
文章目录 AbstractIntroductionContributionRelated Work定向目标检测微小目标检测多尺度学习标签分配上下文信息特征增强MethodOverview动态先验Coarse Prior MatchingFiner Dynamic Posterior MatchingAblation StudyAnalysis不平衡问题的调解可视化速度Conclusionhh 源代码 …...

代码学习记录11
随想录日记part11 t i m e : time: time: 2024.03.04 主要内容:今天的主要内容是深入了解栈和队列中比较难的题录类型:滑动窗口最大值与前 K K K 个高频元素,最后对于这三天学习的队列和栈的知识进行总结。…...

【LeetCode】第 387 场周赛
3069. 将元素分配到两个数组中 I 给你一个下标从 1 开始、包含 不同 整数的数组 nums ,数组长度为 n 。 你需要通过 n 次操作,将 nums 中的所有元素分配到两个数组 arr1 和 arr2 中。在第一次操作中,将 nums[1] 追加到 arr1 。在第二次操作…...
基于 Vue3打造前台+中台通用提效解决方案(下)
47、通用组件 - 倒计时组件 特惠部分存在一个倒计时的功能,所以我们需要先处理对应的倒计时模块,并把它处理成一个通用组件。 那么对于倒计时模块我们又应该如何进行处理呢? 所谓倒计时,其实更多的是一个时间的处理,那么对于时间的处理,此时我们就需要使用到一个第三方…...
Topaz Video AI:一键提升视频品质,智能重塑影像魅力 mac/win版
Topaz Video AI是一款革命性的视频智能处理软件,它利用先进的机器学习和人工智能技术,为视频创作者提供了前所未有的视频增强和修复功能。无论您是专业视频编辑师、摄影师,还是热爱视频创作的爱好者,Topaz Video AI都能帮助您轻松…...

高效办公软件中哪个提醒待办事项更有效
在忙碌的办公环境中,每个人都像是一台精密运转的机器,处理着各种任务和待办事项。而在这其中,总有一些人,他们仿佛拥有超能力般,总是能准时、高效地完成每一项工作。他们的秘密武器是什么呢?答案就是——高…...
牛客练习赛122
D:圆 正着求删除的最小代价不好做,采用逆向思维,求选择一些不相交的线段使得构成一个圆的代价尽量大,最后答案就是所有线段权值之和减去最大代价。 那么如何求这个最大代价呢?显然区间DP 老套路:破环成链࿰…...
软考复习调整策略和学习计划!
根据软考办发布的最新通知,在群里引起了热烈讨论的是2024年度计算机技术与软件专业技术资格(水平)考试的安排。其中,信息系统项目管理师(简称高项)的考试次数从每年两次减少到只有5月份进行,而系…...

1小时网络安全事件报告要求,持安零信任如何帮助用户应急响应?
12月8日,国家网信办起草发布了《网络安全事件报告管理办法(征求意见稿)》(以下简称“办法”)。拟规定运营者在发生网络安全事件时应当及时启动应急预案进行处置。 1小时报告 按照《网络安全事件分级指南》,…...

mysql使用连接池
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、mysql连接池?二、使用步骤1.引入库 前言 提示:这里可以添加本文要记录的大概内容: 例如: 提示:…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
