Matlab小波去噪——基于wden函数的去噪分析
文章目录
- 一、问题描述
- 二、代码
- 问题1:原始信号加6分贝高斯白噪声
- 问题2:确定合适的小波基函数
- 问题3:确定最合适的阈值计算估计方法
- 问题4:确定合适的分解层数
- 问题5:实际信号去噪
- 问题6:对比
- 三、演示视频
- 最后
一、问题描述
1.利用MATLAB绘制原始信号,对其加6分贝高斯白噪声;
2.以Minimaxi阈值法,软阈值函数,3层分解层数,分别用dbN和symN小波对加噪信号去噪,获得分解图和去噪后的图,并用信噪比和均方根误差作为评判标准,确定合适的小波基函数;
3.用第2步确定的小波基函数,软阈值函数,分解层数为3层,对无偏估计阈值(RigrSure)、固定式阈值(Sqtwolog)、启发式阈值(HeurSure)和极大极小阈值(Minimaxi)四种分别去噪,获得去噪后的图,并用信噪比和均方根误差作为评判标准,确定最合适的阈值计算估计方法;
4.用第2步确定的小波基函数,第3步确定的阈值计算估计准则,分别用分解层数为1,2,3,4,5,6对加噪信号进行去噪,获得去噪后得到图,并用信噪比和均方根误差作为评判标准;
5.用实际的信号加6分贝噪声对前面确定的小波基函数,阈值计算方法以及分解层数用小波阈值进行去噪,并求信噪比和均方根误差。
6、确定好小波基函数、阈值函数和分解层数后,分别模拟加入不同量的噪声与4阶巴特沃斯低通滤波器滤波对比
二、代码
问题1:原始信号加6分贝高斯白噪声
代码如下(示例):
clear
clc
close all
%% MATLAB绘制原始信号
load('data.mat'); %私聊发数据
data=data;
%% 加6分贝高斯白噪声
SNR=6; %6dB
noise=0.2*randn(size(data))*std(data)/db2mag(SNR);
s=data+noise;
figure;
subplot(211)
plot(data);ylabel('P/MPa');title('原始信号')
subplot(212)
plot(s);ylabel('P/MPa');title('加6dB高斯白噪声')问题2:确定合适的小波基函数
代码如下(示例):
clear
clc
close all
%% MATLAB绘制原始信号
load('data.mat');
data=data;
%% 加6分贝高斯白噪声
SNR=6; %6dB
noise=0.2*randn(size(data))*std(data)/db2mag(SNR);
s=data+noise;
%% Minimaxi阈值法,软阈值函数,3层分解层数,db5去噪
wname=strvcat('sym4','sym5','db4','db5');
for i=1:4[C,L] = wavedec(s,3,wname(i,:)); %进行3层小波包分解s1=wden(s,'minimaxi','s','mln',3,wname(i,:)); %Minimaxi、软阈值,3层,db5figure;subplot(311)plot(data);xlabel('t/ms');ylabel('P/MPa');title('原始信号')subplot(312)plot(s);xlabel('t/ms');ylabel('P/MPa');title('加6dB高斯白噪声')subplot(313)plot(s1);xlabel('t/ms');ylabel('P/MPa');title(['Minimaxi-软阈值-3层-',wname(i,:)])figuresubplot(511)plot(data,'r');ylabel('s');title([wname(i,:),'小波分解图'])set(gca,'ytick',[]) set(gca,'xtick',[]) subplot(512)plot(C(1:L(2)),'b');ylabel('a3')set(gca,'ytick',[]) set(gca,'xtick',[]) subplot(513)plot(C(L(2):L(3)));ylabel('d3')set(gca,'ytick',[]) set(gca,'xtick',[]) subplot(514)plot(C(L(3):L(4)));ylabel('d2')set(gca,'ytick',[]) set(gca,'xtick',[]) subplot(515)plot(C(L(4):L(5)));ylabel('d1')SNR_s1(i)=snr(data,s1-data);RMSE_s1(i)=sqrt(mse(data-s1)); SNR_s11(i)=snr(s,s1-s);disp(['Minimaxi-软阈值-3层-',wname(i,:),':信噪比=',num2str(SNR_s1(i)),'dB,均方根误差=',num2str(RMSE_s1(i))])disp(['加噪后信噪比=',num2str(SNR_s11(i)),'dB'])disp('-----------------------------------------------------------')
end
%% 根据SNR选取较好的小波基函数
[m,index]=max(SNR_s1);
disp(['最合适的阈值计算估计方法为:',wname(index,:)])
disp('-----------------------------------------------------------')
问题3:确定最合适的阈值计算估计方法
代码如下(示例):
clear
clc
close all
%% MATLAB绘制原始信号
load('data.mat');
data=data;
%% 加6分贝高斯白噪声
SNR=6; %6dB
noise=0.2*randn(size(data))*std(data)/db2mag(SNR);
s=data+noise;
%% main2已经确定最合适的小波基函数
wname='sym5';
%% 无偏估计阈值(RigrSure)、固定式阈值(Sqtwolog)、启发式阈值(HeurSure)和极大极小阈值(Minimaxi)
TPTR=['rigrsure';'sqtwolog';'heursure';'minimaxi'];
for i=1:4s3=wden(s,TPTR(i,:),'s','mln',3,wname); %依次进行滤波figuresubplot(311)plot(data);xlabel('t/ms');ylabel('P/MPa');title('原始信号')subplot(312)plot(s);xlabel('t/ms');ylabel('P/MPa');title('加6dB高斯白噪声')subplot(313)plot(s3);xlabel('t/ms');ylabel('P/MPa');title(['采用',TPTR(i,:),'进行滤波'])snr_s3(i)=snr(data,s3-data);RMSE_s3(i)=sqrt(mse(data-s3));snr_s33(i)=snr(s,s3-s);disp([TPTR(i,:),'-软阈值-3层-',wname,':信噪比=',num2str(snr_s3(i)),'dB,均方根误差=',num2str(RMSE_s3(i))])disp(['加噪后信噪比=',num2str(snr_s33(i)),'dB'])disp('-----------------------------------------------------------')
end
%% 根据SNR选取较好的阈值计算估计方法
[m,index]=max(snr_s3);
disp(['最合适的阈值计算估计方法为:',TPTR(index,:)])
disp('-----------------------------------------------------------')
问题4:确定合适的分解层数
代码如下(示例):
clear
clc
close all
%% MATLAB绘制原始信号
load('data.mat');
data=data;
%% 加6分贝高斯白噪声
SNR=6; %6dB
noise=0.2*randn(size(data))*std(data)/db2mag(SNR);
s=data+noise;
%% main2和main3确定的小波基函数和阈值计算估计方法
wname='sym5';
TPTR='sqtwolog';
%% 分解层数为1,2,3,4,5,6
for i=1:6s4=wden(s,TPTR,'s','mln',i,wname); %依次进行滤波figuresubplot(311)plot(data);xlabel('t/ms');ylabel('P/MPa');title('原始信号')subplot(312)plot(s);xlabel('t/ms');ylabel('P/MPa');title('加6dB高斯白噪声')subplot(313)plot(s4);xlabel('t/ms');ylabel('P/MPa');title(['分解层数=',num2str(i)])snr_s4(i)=snr(data,s4-data);RMSE_s4(i)=sqrt(mse(data-s4));snr_s44(i)=snr(s,s4-s);disp([TPTR,'-软阈值-',num2str(i),'层-',wname,':信噪比=',num2str(snr_s4(i)),'dB,均方根误差=',num2str(RMSE_s4(i))])disp(['加噪后信噪比=',num2str(snr_s44(i)),'dB'])disp('-----------------------------------------------------------')
end
%% 根据SNR选取较好的分解层数
[m,index]=max(snr_s4);
disp(['最合适的分解层数为:',num2str(index)])
disp('-----------------------------------------------------------')
问题5:实际信号去噪
代码如下(示例):
clear
clc
close all
%% 读取实际的信号
data=xlsread('14#c1.csv');
data=data(:,2);
%% 加6分贝高斯白噪声
SNR=6; %6dB
noise=0.2*randn(size(data))*std(data)/db2mag(SNR);
s=data+noise;
%% 根据(2)(3)(4)确定参数
wname='sym5';
TPTR='sqtwolog';
lev=6;
%% 进行滤波
s5=wden(s,TPTR,'s','mln',lev,wname); %进行滤波
%% 绘制
figure;
subplot(311)
plot(data);xlabel('t/ms');ylabel('P/MPa');title('实际信号')
subplot(312)
plot(s);xlabel('t/ms');ylabel('P/MPa');title('加6dB高斯白噪声')
subplot(313)
plot(s5);xlabel('t/ms');ylabel('P/MPa');title('信号去噪')
snr_s55=snr(s,s5-s);
snr_s5=snr(data,s5-data);RMSE_s5=sqrt(mse(data-s5));
disp([TPTR,'-软阈值-',num2str(lev),'层-',wname,':信噪比=',num2str(snr_s5),'dB,均方根误差=',num2str(RMSE_s5)])
disp(['加噪后信噪比=',num2str(snr_s55),'dB'])
问题6:对比
代码如下(示例):
clear
clc
close all
%% 读取实际的信号
data=xlsread('14#c1.csv');
data=data(:,2);
fs=125000;
%%
wname='sym5';
TPTR='sqtwolog';
lev=6;
%% 设计4阶巴特沃斯低通滤波器
fc=10000;
n=4; %阶数
[b,a]=butter(n,fc/(fs/2), 'low');
%% 加1-16分贝高斯白噪声
for SNR=1:16 %6dBnoise=0.2*randn(size(data))*std(data)/db2mag(SNR);s=data+noise;s1=filter(b,a,s); %filter既能进行IIR滤波又能进行FIR滤波s2=wden(s,TPTR,'s','mln',lev,wname); %进行滤波snr_s1(SNR)=snr(data,s1-data);RMSE_s1(SNR)=sqrt(mse(data-s1));snr_s2(SNR)=snr(data,s2-data);RMSE_s2(SNR)=sqrt(mse(data-s2));
end
figure;
plot(1:16,snr_s1,'o-r');
hold on
plot(1:16,snr_s2,'*-b');
xlabel('高斯白噪声dB');ylabel('SNR')
legend('FIR滤波','小波滤波')
title('信噪比曲线')
%%
for SNR=2:2:10 %6dBnoise=0.2*randn(size(data))*std(data)/db2mag(SNR);s=data+noise;s1=filter(b,a,s); %filter既能进行IIR滤波又能进行FIR滤波s2=wden(s,TPTR,'s','mln',lev,wname); %进行滤波figure;subplot(411)plot(data);xlabel('t/ms');ylabel('P/MPa');title('实际信号')subplot(412)plot(s);xlabel('t/ms');ylabel('P/MPa');title('加16dB高斯白噪声')subplot(413)plot(s1);xlabel('t/ms');ylabel('P/MPa');title('FIR信号去噪')subplot(414)plot(s1);xlabel('t/ms');ylabel('P/MPa');title('小波信号去噪')suptitle(['噪声大小=',num2str(SNR),'dB'])
end三、演示视频
基于wden函数的去噪演示
最后
不定期发布一些matlab设计内容,敬请期待。包括但不限于如下内容:信号处理、通信仿真、gui设计、matlab appdesigner,simulink仿真。有任何有关MATLAB的问题可🐧咨询

相关文章:

Matlab小波去噪——基于wden函数的去噪分析
文章目录一、问题描述二、代码问题1:原始信号加6分贝高斯白噪声问题2:确定合适的小波基函数问题3:确定最合适的阈值计算估计方法问题4:确定合适的分解层数问题5:实际信号去噪问题6:对比三、演示视频最后一、…...

分布式对象存储——Apache Hadoop Ozone
前言 本文隶属于专栏《大数据技术体系》,该专栏为笔者原创,引用请注明来源,不足和错误之处请在评论区帮忙指出,谢谢! 本专栏目录结构和参考文献请见大数据技术体系 1. 概述 Ozone是Apache Hadoop项目的子项目…...

Linux 和数据库笔记-03
今天主要内容数据库相关介绍数据库(软件)常见类型Navicat 工具基本使用常见的数据类型和约束(重点)SQL 语句的编写(表和数据)一. 数据库是什么?为什么学习数据库软件中产生的所有数据, 最终都要存储于数据库当中测试人员如果想要进行数据查询/数据校验, 就必须掌握对数据库的基…...
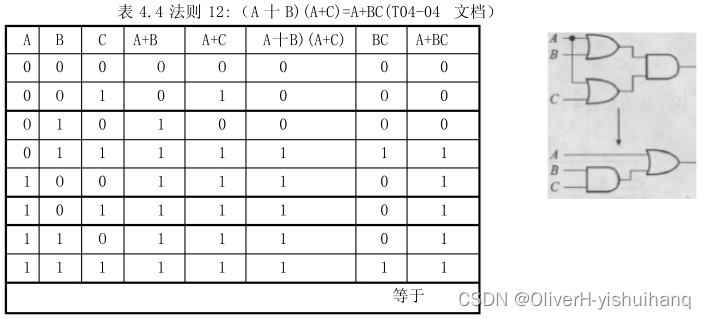
布尔定律---布尔代数的基本定律
一、单变量布尔定律 1、0-1定律 2、互补定律 3、重叠定律 4、还原定律 小结:或运算和与运算定律的差别在于:所有的“|”运算符换成“&”,运算结果为 0 换成 1。这就是对偶定律。它不仅是单逻辑变量的定律,而且对于所有布尔定…...

OSG三维渲染引擎编程学习之七十五:“第七章:OSG场景图形交互” 之 “7.6 多视图”
目录 第七章 OSG场景图形交互 7.6 多视图 7.6.1 多视图描述 7.6.2 多视图相机示例 第七章 OSG场景图形交互 作为一个成熟的三维渲染引擎,需...
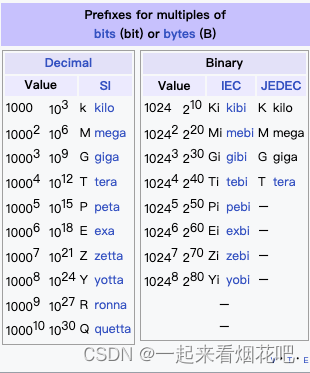
【计算机】单位制前缀的歧义-KB、kb、MB混用
引言 经常遇到容量、带宽的单位,MB,GB在进行单位换算时,总是傻傻分不清,查些资料浅记录一下。 公制(metric system) 又译米制,是一个国际化十进位量度系统。法国在1799年开始使用公制…...

nodejs调用浏览器打开URL链接
本文主要介绍的是node.js调用Chrome浏览器/默认浏览器打开链接地址的相关内容,分享出来供大家参考学习,下面来一起看看详细的介绍: 安装第三方插件open 通过open模块,可以在任何平台上打开某个浏览器网址。 通过NPM安装 npm i…...
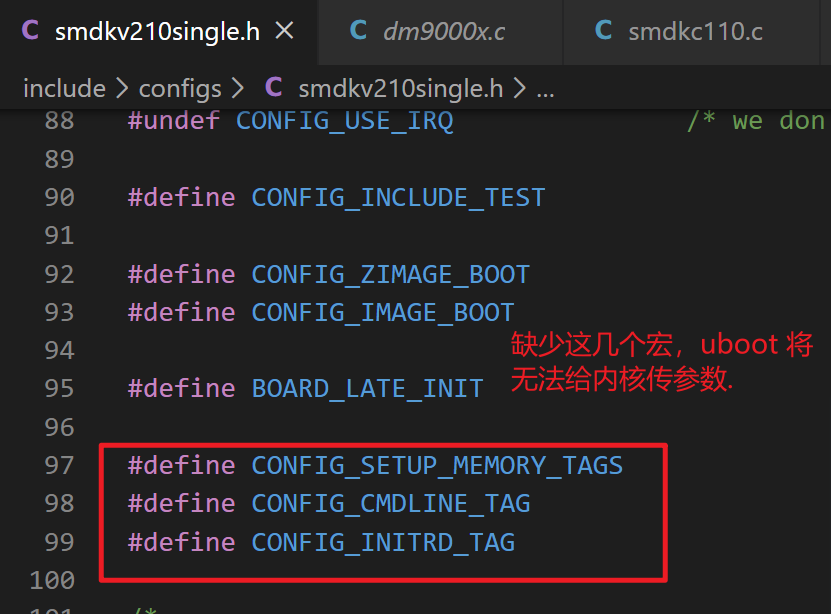
ARM uboot 的移植2-从三星官方 uboot 开始移植
一、inand 驱动问题的解决 1、先从现象出发定位问题 (1) 解决问题的第一步,是定位问题。所谓定位问题,就是找到源代码当中导致这个问题的那一句或者那几句代码。有时候解决这个问题需要修改的代码和直接导致这个问题的代码是不同的。我们这里说的定位问…...

js作用域和作用域链
1、局部作用域分为函数作用域和块作用域 1.1、函数作用域: 在函数内部声明的变量只能在函数内部被访问,外部无法直接访问。 总结 1.函数内部声明的变量,在函数外部无法被访问 2.函数的参数也是函数内部的局部变量 3.不同函数内部声明的变量无法互相访…...

C语言字符串
目录 一、字符串的引入和注意事项 1.1 字符串定义的几种方式: 1.2 定义字符串的方法一和方法二的区别: 1.3 字符串输出的几种方式: 1.3.1 循环下标法遍历输出字符串: 1.3.2 转义字符%s输出字符串: 1.3.3 使用puts函…...

Eureka注册中心快速入门
一、提供者与消费者**服务提供者:**一次业务中,被其他微服务调用的服务。(提供接口给其他微服务)**服务消费者:**一次业务中,调用其他微服务的服务。(调用其它微服务提供的接口)比如…...

xmu 离散数学 卢杨班作业详解【1-3章】
文章目录第一章 命题逻辑常用latex数学公式1.4.5679101113171923242627第二章 一阶逻辑1.2.3.6.9.10.12.13.一阶逻辑推理理论12.13.15.第三章 集合2478101213.第一章 命题逻辑 常用latex数学公式 符号代码∨\vee∨$\vee$∧\wedge∧$\wedge$→\rightarrow→$\rightarrow$⇒\Ri…...
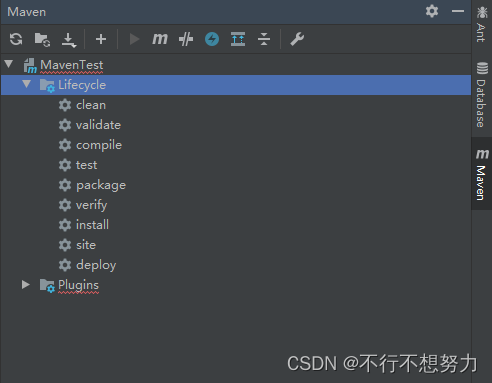
mvn命令
在IDEA右侧Maven菜单中,有以下几种指令。 clean:清理,清除上一次构建生产的文件。执行该命令会删除项目地址下的target文件,但不会删除本地的maven已生成的文件。 validate:验证,验证项目是否正确且所有必…...

JS - 事件循环EventLoop
一、面试题:说一下事件循环(回答思路梳理) 首先 js 是单线程运行的( JS 可以修改 DOM,如果在 JS 执行的时候 UI 线程还在工作,就可能导致不能安全的渲染 UI),在代码执行的时候&…...

【Java基础】30分钟Git 从入门到精通
一、 版本控制工具1、什么是版本控制系统?版本控制系统(Version Control System):是一种记录一个或若干文件内容变化,以便将来查阅特定版本修订情况的系统。版本控制系统不仅可以应用于软件源代码的文本文件,而且可以对…...

0100 MySQL03
1.distinct关键字 把查询结果去除重复记录,原表数据不会被修改,只能出现在字段的最前端 select distinct job from emp; select distinct job,deptno from emp;//表示两个字段联合起来 去重 2.连接查询 从一张表中单独查询,称为单表查询 两张表联合…...

32- PyTorch基础 (PyTorch系列) (深度学习)
知识要点 PyTorch可以说是现阶段主流的深度学习框架 . 1 PyTorch入门 1.1 PyTorch概述 Torch是什么?一个火炬!其实跟Tensorflow中Tensor是一个意思,可以当做是能在GPU中计算的矩阵.,也可以当做是ndarray的GPU版! PyT…...
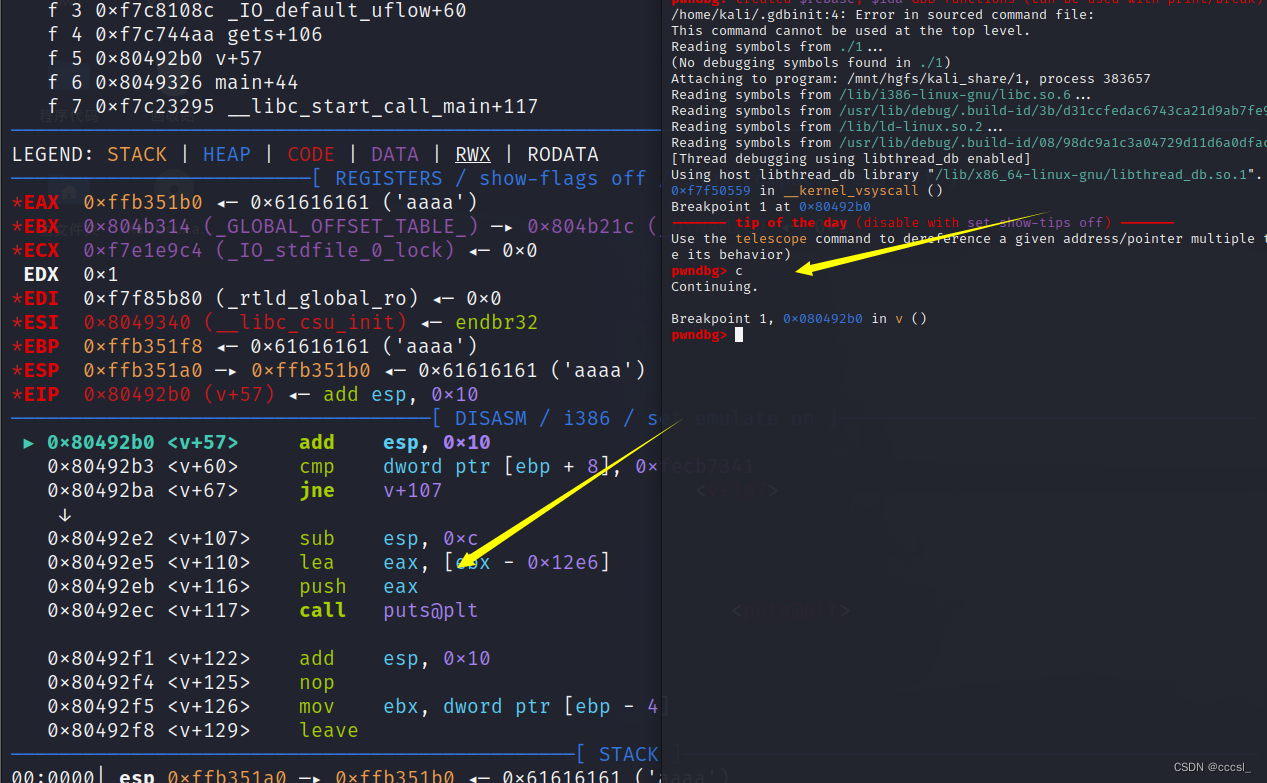
用gdb.attach()在gdb下断点但没停下的情况及解决办法
在python中,如果导入了pwntools,就可以使用里面的gdb.attach(io)的命令来下断点。 但是这一次鼠鼠遇到了一个情况就是下了断点,但是仍然无法在断点处开始运行,奇奇怪怪。 这是我的攻击脚本 我们运行一下。 可以看到其实已经运行起…...
调度(本质仍然是进程))
Linux入门篇-作业(jobs)调度(本质仍然是进程)
简介 之所以叫做作业调度,作业是以shell为单位的,一个shell建立的作业,不会被另外一个shell看到(包 括root),但是仍然可以看到作业对应的进程。①前台进程(front process) 运行在用户…...

vue 监听 取消监听
vue 的 watch 除了可以使用声明式的配置项以外,还可以通过命令式 this.$watch 方法。 如下是我们比较少用的命令式(想要初始只监听一次,必须命令式写法): 监听只运行一次 声明式 export default{data: {showType: fa…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
