LeetCode 1976.到达目的地的方案数:单源最短路的Dijkstra算法
【LetMeFly】1976.到达目的地的方案数:单源最短路的Dijkstra算法
力扣题目链接:https://leetcode.cn/problems/number-of-ways-to-arrive-at-destination/
你在一个城市里,城市由 n 个路口组成,路口编号为 0 到 n - 1 ,某些路口之间有 双向 道路。输入保证你可以从任意路口出发到达其他任意路口,且任意两个路口之间最多有一条路。
给你一个整数 n 和二维整数数组 roads ,其中 roads[i] = [ui, vi, timei] 表示在路口 ui 和 vi 之间有一条需要花费 timei 时间才能通过的道路。你想知道花费 最少时间 从路口 0 出发到达路口 n - 1 的方案数。
请返回花费 最少时间 到达目的地的 路径数目 。由于答案可能很大,将结果对 109 + 7 取余 后返回。
示例 1:
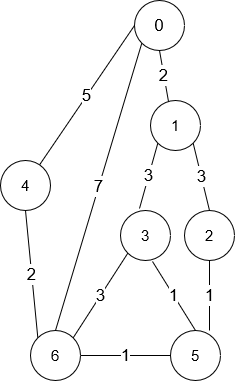
输入:n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]] 输出:4 解释:从路口 0 出发到路口 6 花费的最少时间是 7 分钟。 四条花费 7 分钟的路径分别为: - 0 ➝ 6 - 0 ➝ 4 ➝ 6 - 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6 - 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6
示例 2:
输入:n = 2, roads = [[1,0,10]] 输出:1 解释:只有一条从路口 0 到路口 1 的路,花费 10 分钟。
提示:
1 <= n <= 200n - 1 <= roads.length <= n * (n - 1) / 2roads[i].length == 30 <= ui, vi <= n - 11 <= timei <= 109ui != vi- 任意两个路口之间至多有一条路。
- 从任意路口出发,你能够到达其他任意路口。
方法一:单源最短路的Dijkstra算法
“单源最短路”意思是从一个点出发到其他点的最短路径。单源最短路的Dijkstra算法也可以看我之前做的视频。
总之Dijkstra算法就是,我们从起点开始:
计算所有能一步到达的点中,哪个点距离起点最近。
下一步就走到这个点,然后能一步到达的点就更新了。
直到走完所有的点为止。
对于这道题,我们在“往前走”的同时,记录一下走到这一步的“方案数”:
- 若从当前点走到点
a的距离 小于a原本到起点的距离,则说明发现了新大“路”(更近的路)。舍弃掉之前的方案数,将点a的方案数变为当前点的方案数,并更新最短距离,可以从点a开始往深处继续探索。 - 若从当前点走到点
a的距离 等于a原本到起点的距离,则说明又发现了一条同为最近路的路。将点a的方案数加上当前点的方案数。 - 否则,已有更短路,不做考虑。
最终返回终点的路径数即为答案。
- 时间复杂度 O ( m log m ) O(m\log m) O(mlogm)
- 空间复杂度 O ( n + m ) O(n+m) O(n+m)
AC代码
C++
typedef long long ll;
const ll MOD = 1e9 + 7;class Solution {
public:int countPaths(int n, vector<vector<int>>& roads) {vector<vector<pair<int, int>>> graph(n);for (vector<int>& road : roads) {graph[road[0]].push_back({road[1], road[2]});graph[road[1]].push_back({road[0], road[2]});}vector<ll> way(n);way[0] = 1;vector<ll> dis(n, 1e18);dis[0] = 0;priority_queue<pair<ll, int>, vector<pair<ll, int>>, greater<pair<ll, int>>> pq;pq.push({0, 0});while (pq.size()) {auto [thisDistance, thisNode] = pq.top();pq.pop();if (thisDistance > dis[thisNode]) { // 有更优解了continue;}for (auto [nextNode, nextDistance] : graph[thisNode]) {if (thisDistance + nextDistance < dis[nextNode]) {dis[nextNode] = thisDistance + nextDistance;way[nextNode] = way[thisNode];pq.push({dis[nextNode], nextNode});}else if (thisDistance + nextDistance == dis[nextNode]) {way[nextNode] = (way[nextNode] + way[thisNode]) % MOD;}}}return way.back();}
};
Python
# from typing import List
# import heapqMOD = int(1e9) + 7class Solution:def countPaths(self, n: int, roads: List[List[int]]) -> int:graph = [[] for _ in range(n)]for x, y, d in roads:graph[x].append((y, d))graph[y].append((x, d))way = [0] * nway[0] = 1dis = [int(1e18)] * ndis[0] = 0pq = [(0, 0)]while pq:thisDistance, thisNode = heapq.heappop(pq)if thisDistance > dis[thisNode]:continuefor nextNode, nextDistance in graph[thisNode]:if nextDistance + thisDistance < dis[nextNode]:dis[nextNode] = nextDistance + thisDistanceway[nextNode] = way[thisNode]heapq.heappush(pq, (dis[nextNode], nextNode))elif nextDistance + thisDistance == dis[nextNode]:way[nextNode] = (way[nextNode] + way[thisNode]) % MODreturn way[-1]
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/136481215
相关文章:

LeetCode 1976.到达目的地的方案数:单源最短路的Dijkstra算法
【LetMeFly】1976.到达目的地的方案数:单源最短路的Dijkstra算法 力扣题目链接:https://leetcode.cn/problems/number-of-ways-to-arrive-at-destination/ 你在一个城市里,城市由 n 个路口组成,路口编号为 0 到 n - 1 ÿ…...
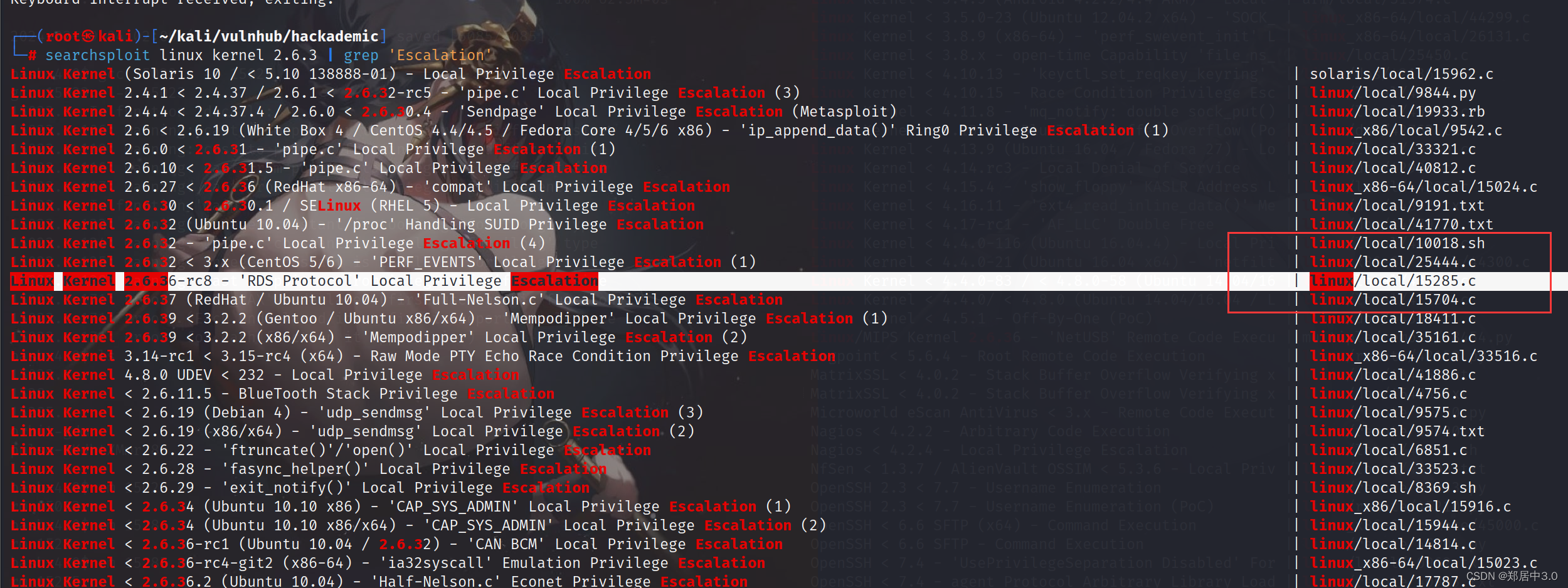
vulnhub-----Hackademic靶机
文章目录 1.C段扫描2.端口扫描3.服务扫描4.web分析5.sql注入6.目录扫描7.写马php反弹shell木马 8.反弹shell9.内核提权 1.C段扫描 kali:192.168.9.27 靶机:192.168.9.25 ┌──(root㉿kali)-[~] └─# arp-scan -l Interface: eth0,…...

十秒学会Ubuntu命令行:从入门到进阶
一、引言 在使用Ubuntu操作系统时,命令行界面(CLI)是不可或缺的一部分。对于初学者来说,掌握基本的命令行操作可以帮助他们更高效地管理系统和软件。 本文将介绍一些常见的Ubuntu命令以及如何解决与命令行相关的问题。 目录 一、…...
华为智慧教室3.0的晨光,点亮教育智能化变革
“教室外有更大的世界,但世界上没有比教室更伟大的地方。” 我们在求学阶段,都听说过这句话,但往往是在走出校园之后,才真正理解了这句话。为了让走出校园的孩子能够有能力,有勇气探索广阔的世界。我们应该准备最好的教…...

深度学习预测分析API:金融领域的Game Changer
🚀 引言 在这个AI遍地开花的时代,谁能成为金融领域的真正Game Changer?那必然是是深度学习预测分析API。如大脑般高效运转的系统不仅颠覆了传统操作,更是以无与伦比的速度和精度赋予了金融数据以全新的生命。 💼 广泛…...

外贸网站做Google SEO 用wordpress模板的优势
易于优化:WordPress模板是专门为搜索引擎优化(SEO)设计的。从一开始,WordPress模板就考虑到了搜索引擎的因素,因此在构建网站时已经考虑了如何优化网站的结构和内容。使用WordPress模板可以简化优化过程,让您的网站更容易被搜索引…...

后端面试题整理-1
1.Maven 依赖传递产生版本冲突怎么解决? 升级或降级依赖版本:通过修改相关依赖的版本号,选择与项目其他依赖兼容的版本。可以通过查看 Maven 依赖树来确定哪些依赖冲突,并找出合适的版本号进行调整。排除依赖:对于特定…...

Python图像处理之光斑分析
文章目录 质心目标截取光斑半径 python图像处理教程:初步📷插值变换📷形态学处理📷滤波 光斑是工程中经常出现的图像数据,其特点是目标明确,分布清晰。对光斑图像的分析,主要包括质心定位、目标…...

软件测试 - 测试用例基本理论
1. 概念 为了特定的目的(该目的是检验代码是否满足用户需求)而设计的文档,文档包含测试输入、执行条件、预期结果等。文档的形式一般是excel表格。 比如说我们买了一台电脑,新买的笔记本检查完外观之后第一步需要查看电脑是否能够正常开机,…...

在 Flutter 中使用 flutter_gen 简化图像资产管理
你是否厌倦了在 Flutter 项目中手动管理图像资产的繁琐任务? 告别手工输入资源路径的痛苦,欢迎使用“Flutter Gen”高效资源管理的时代。在本文中,我将带您从手动处理图像资源的挫折到动态生成它们的便利。 选择1:痛苦手动添加–…...
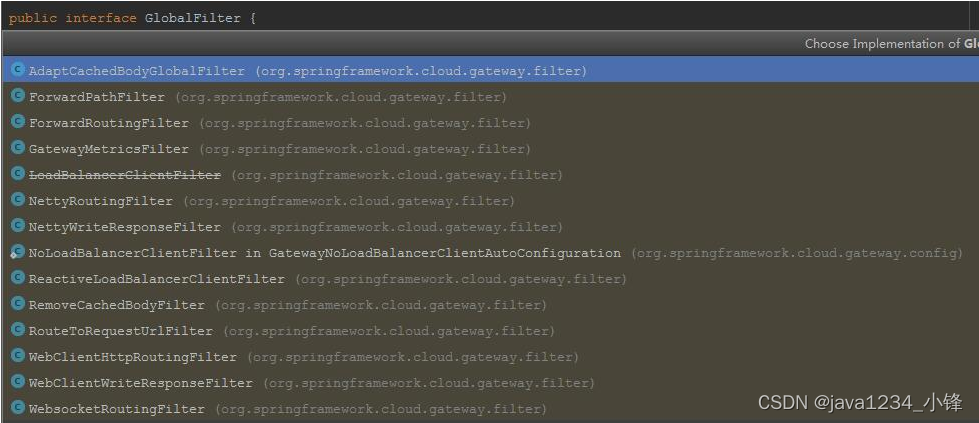
两天学会微服务网关Gateway-Gateway过滤器
锋哥原创的微服务网关Gateway视频教程: Gateway微服务网关视频教程(无废话版)_哔哩哔哩_bilibiliGateway微服务网关视频教程(无废话版)共计17条视频,包括:1_Gateway简介、2_Gateway工作原理、3…...
图像处理 mask掩膜
1,图像算术运算 图像的算术运算有很多种,比如两幅图像可以相加,相减,相乘,相除,位运算,平方根,对数,绝对值等;图像也可以放大,缩小,旋…...
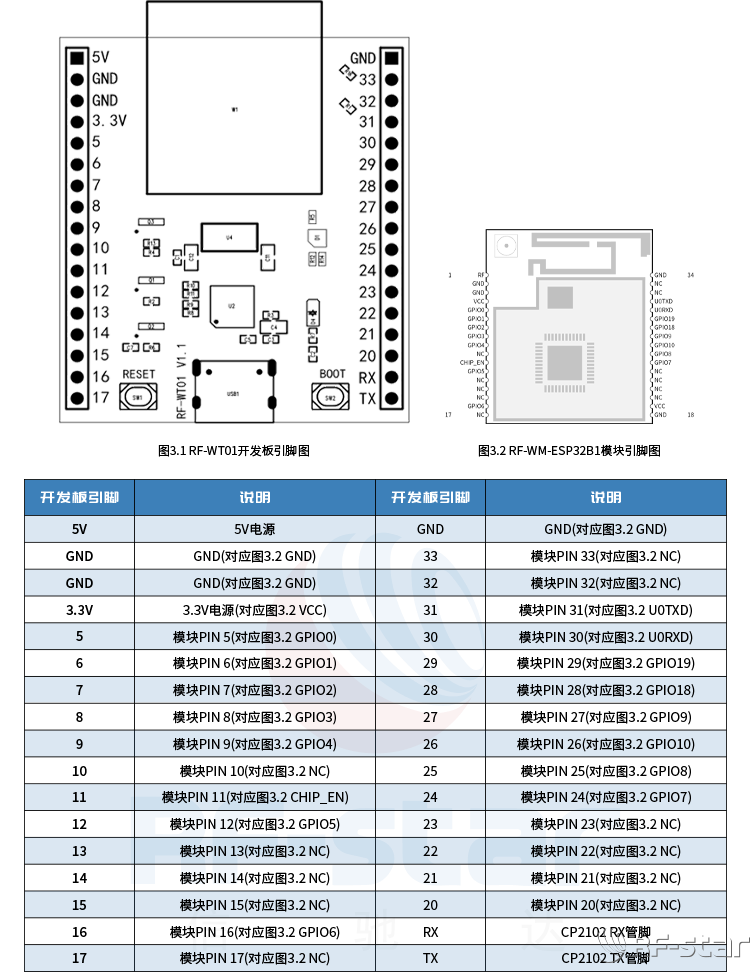
信驰达ESP32-C3/RTL8720CM WiFi开发板RF-WT01上线
为方便客户快速选型和验证WiFi模块,深圳市信驰达科技有限公司推出了WiFi开发板RF-WT01,支持适配信驰达RF-WM-ESP32B1、RF-WM-20CMB1、RF-WM-11AFB1、RF-WM-20DNB1 4款WiFi串口模块使用,方便客户实现对信驰达WiFi模块的快速测试和评估。 图1RF…...

【产品经理方法论——产品的基本概念】
1. 产品学三元素 产品学有三个元素:用户、需求、产品 产品学的内容:根据用户的需求设计产品,使用产品服务用户 仅仅通过三个元素无法说明每个元素的概念,因为三个元素互为说明关系。 通过引入人/群体来说明三个元素的关系。 需…...
V2 查询用户信息)
推特API(Twitter API)V2 查询用户信息
前面章节已经介绍使用code换取Token的整个流程了,这里不再重复阐述了,下面我们介绍如何使用Token查询用户信息等操作。 1.引入相关依赖Maven <dependency> <groupId>oauth.signpost</groupId> <artifactId>signpost-co…...

在Elasticsearch IK分词器中更新、停用某些专有名词
在Elasticsearch IK分词器中更新、停用某些专有名词 目前IK分词器对于现有的新名词或者流行语没有做区分比如"白嫖" “奥利给”,或者对一些没有用的字比如 “的” "地"进行分词其实没有必要过多的分词只会占用宝贵的内存空间,所以如…...

时钟显示 html JavaScript
sf.html <!DOCTYPE html> <html><head><meta charset"UTF-8"><title>时间</title><script>function showTime(){var timenew Date();var datetime.getDate();var yeartime.getFullYear();var monthtime.getMonth()1;var …...

List<Object>集合对象属性拷贝工具类
目录 问题现象: 问题分析: 解决方法: 问题现象: 最近在项目中经常会使用到BeanUtils工具类来作对象的属性字段拷贝,但如果应用到List集合的话就需要遍历去操作了,如下: 打印结果: …...

请说明Vue中的异步组件加载
Vue中的异步组件加载是指当页面需要渲染某个组件时,可以在需要时再去加载这个组件,而不是在页面初始化的时候就将所有组件一次性加载进来。这种方式能够有效降低页面的初始加载时间,提升用户体验。 在Vue中,我们可以使用import函…...
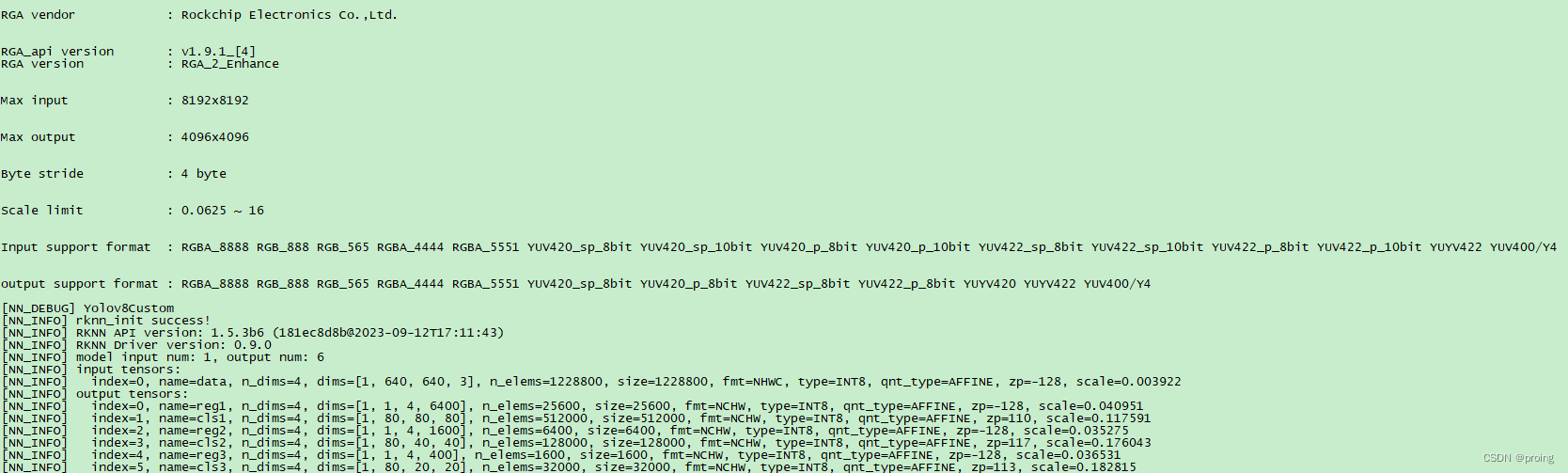
目标检测5:采用yolov8, RK3568上推理实时视频流
上一个效果图,海康球机对着电脑屏幕拍,清晰度不好。 RK3568接取RTSP视频流,通过解码,推理,编码,最终并把结果推出RTSP视频流。 数据集采用coco的80个种类集,通过从yovo8.pt,转换成R…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
