小米消金剖析“冒充老板”诈骗案例,呼吁群众提高反诈意识
近年来,诈骗手段日益翻新,冒充公司老板身份进行诈骗的案例屡见不鲜。不法分子利用人们的焦虑心理,以冒充老板的身份进行诈骗,给无数工作人员和企业带来了巨大的经济损失。重庆小米消费金融有限公司(以下简称“小米消金”)结合真实案例深度剖析,分享预防冒充“老板”诈骗的重要方法,共同守护企业和个人的财产安全。
案件回顾:2024年1月29日,某公司财务人员Z小姐接到自称为公司“老板”、“老板娘”的QQ好友添加申请,申请通过后被拉进一QQ群。老板在群里发布指令,“你现在把公司账上全部资金打到XXXXXXXXXXXX这个银行账号上”,并催促道,“这是XX合同的预付款比较着急,尽快转账”。就这样,Z小姐信以为真,并按照要求完成转账。殊不知该账户为诈骗账户,导致公司遭受重大经济损失。
在此类诈骗案件中,骗子通过非法获取公司信息,研究组织架构、人员信息,伪装成银行工作人员、公司领导等,通过QQ、微信添加公司工作人员为好友。其次,骗子能准确说出受害人姓名等信息,让受害人卸下防备,随后以各种理由提出转账的要求,例如要给客户转账、支付设备款项等。最后,骗子利用员工敬畏领导、不敢冒昧跟领导核实的心理实施诈骗,频繁使用“尽快、立即”等催促性的词语,降低受害人核实转账需求真假的可能性。
小米消金提示,在社交媒体平台上,如微信、QQ等,如果有陌生人主动添加你,尤其是声称是公司领导、同事或合作伙伴的人,一定要保持警惕。第一,务必核实对方身份信息,最好通过打电话或者当面确认的方式核实清楚。第二,不要轻易点击或者下载对方发来的不明链接。第三,转账有风险,在进行转账操作时,务必保持高度警惕,转账之前应先核对收款人账号和相关信息,确保准确无误后再进行操作。一旦遭遇QQ诈骗,要第一时间向公安机关报警求助。
小米消金通过普及金融服务相关知识,让大家更好地共享金融改革发展成果的同时,提升大家的获得感、幸福感、安全感。下一步,小米消金将持续聚焦消费者需求,全力推动开展丰富多彩的金融知识教育宣传活动,多措并举提高活动的影响力和覆盖面,积极履行企业社会责任,助力社会和谐健康发展。
相关文章:

小米消金剖析“冒充老板”诈骗案例,呼吁群众提高反诈意识
近年来,诈骗手段日益翻新,冒充公司老板身份进行诈骗的案例屡见不鲜。不法分子利用人们的焦虑心理,以冒充老板的身份进行诈骗,给无数工作人员和企业带来了巨大的经济损失。重庆小米消费金融有限公司(以下简称“小米消金…...

全量知识系统问题及SmartChat给出的答复 之14 解析器+DDD+文法型 之2
Q36. 知识系统中设计的三种文法解析器和设计模式之间的关系 进一步,我想将 知识系统中设计的三种语言(形式语言、人工语言和自然)的文法解析器和DDD中的三种程序类型(领域模型、领域实体和领域服务) 形式语言文法 我…...
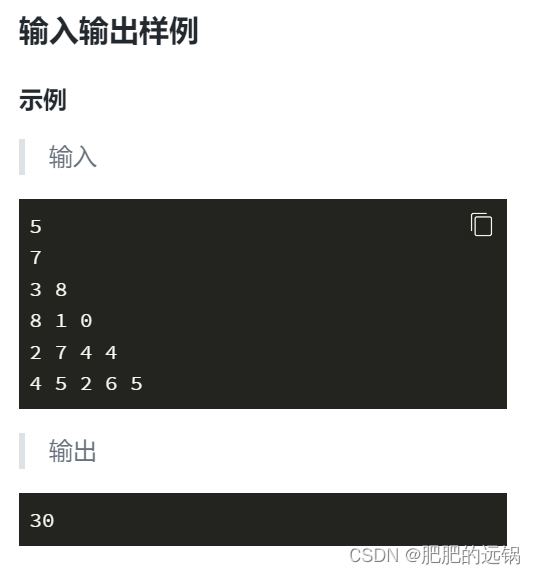
蓝桥杯备赛 day2 | 4. 付账问题 5. 数字三角形
付账问题,关键是要了解整型的范围,确定获取输入数据的变量类型 需要注意的是int的十进制范围-32768 ~ 32767,那么我们可以知道,人数n是可以用int来装的,需付款数S应该是long long,获取的每个人初始钱数也应…...
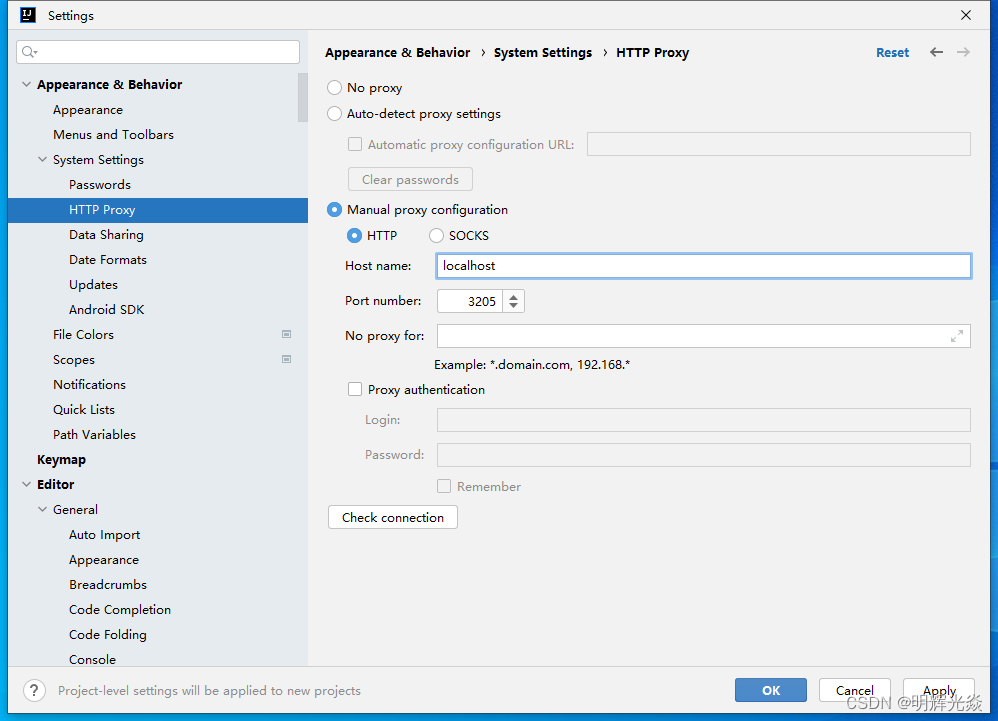
2024关于idea激活码报This license xxxx has been suspended
HOSTS文件中增加 0.0.0.0 www.jetbrains.com 0.0.0.0 account.jetbrains.com 然后...
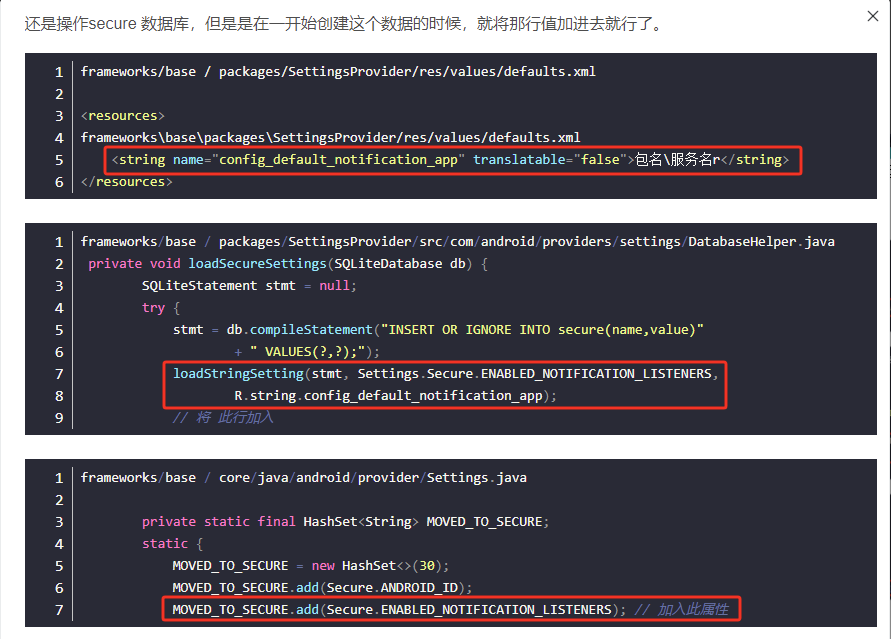
Android9-W517-使用NotificationListenerService监听通知
目录 一、前言 二、前提 三、方案 方案一 方案二 方案三 方案四 方案五 方案六 方案七 四、关于NotificationListenerService类头注释 五、结论 一、前言 NotificationListenerService可以让应用监听所有通知,但是无法获得监听通知的权限,如…...

git的“You can‘t push commits with committe“解决方法
如果使用错误的用户和邮箱执行了git提交,在执行 git push 时将遇到如下错误: ! [remote rejected] feature_116390305_story_0 -> feature_116390305_story_0 (You cant push commits with committer ‘yijian’ or email eyjianqq.com who is not ex…...
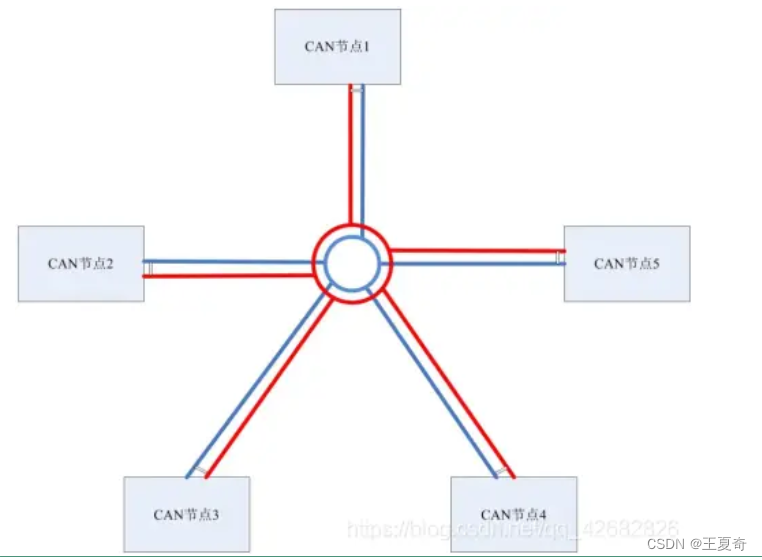
CAN总线的拓扑类型和CAN收发器(原理讲解)
1:CAN收发器(原理讲解) 从原理上来讲CAN_H拉升电压,或CAN_L拉低电压的原理。 以上是TJA1145AT的俯瞰图,此芯片是NXP比较先进的CAN收发器,带SPI总线系统。 回到正题,CAN_H和CAN_L收发器是通过内…...
如何实现WordPress后台显示文章、分类目录、标签等的ID?
我们平时在使用WordPress的过程中,偶尔需要用到文章的ID,或分类目录ID,或标签ID,或媒体库ID,或评论ID,或用户ID等,但是WordPress后台默认是不显示它们的ID的。 今天boke112百科就跟大家分享如何…...
)
【GB28181】SIP协议实践之Windows下VS2019编译eXosip、osip,测试(附工程源码,一键打开编译)
引言 SIP开源库或者GB28181,这里选择了osip和eXosip,但是这两个库的编译使用有些麻烦,源码下来之后编译会出现很多问题,网上也没有找到完整的编译介绍,只能一步一步的找办法解决,以下帮大家整理编译过程。 如果不想编译,可以跳转文章末尾链接直接下载相应工程直接编译即…...

GPT提示语格式——个人自用
总体格式 指令:将 输入 划分为/翻译为/提取出/... 输出 输出格式:... 输入示例:... 输出示例:... 输入:... 输出:基本概述 示例 指令: 提取以下文本中的介词。 输入:“虽然这些发展…...

MCU最小系统电路设计(以STM32F103C8T6为例)
目录 一、何为最小系统? 二、最小系统电路设计 1.电源 (1)各种名词解释 (2)为什么会有VDD_1 _2 _3区分? (3)Mirco USB (4)5v->3.3v滤波电路 &#…...

[JavaWeb学习日记]JSP+Cookie+Filter与登录+CRUD案例
目录 一.JSP 二.EL表达式与JSTL标签 三.Cookie 四.Session 五.Filter 六. 登录CRUD:品牌增删改查案例 Demo一览 1.导包 2.构建包结构 3.创建数据库表tb_brand与user 4.创建实体类 5.mybatis的配置文件和logback配置文件 6.写接口 7.工具类:生成图片与…...

Ruby网络爬虫教程:从入门到精通下载图片
概述 网络爬虫技术在信息时代扮演着重要的角色,它可以自动化地获取互联网上的信息,为用户提供便利的数据服务。本文将带领读者从零开始,通过学习Ruby编程语言,逐步掌握网络爬虫的设计与实现,重点介绍如何利用网络爬虫技…...
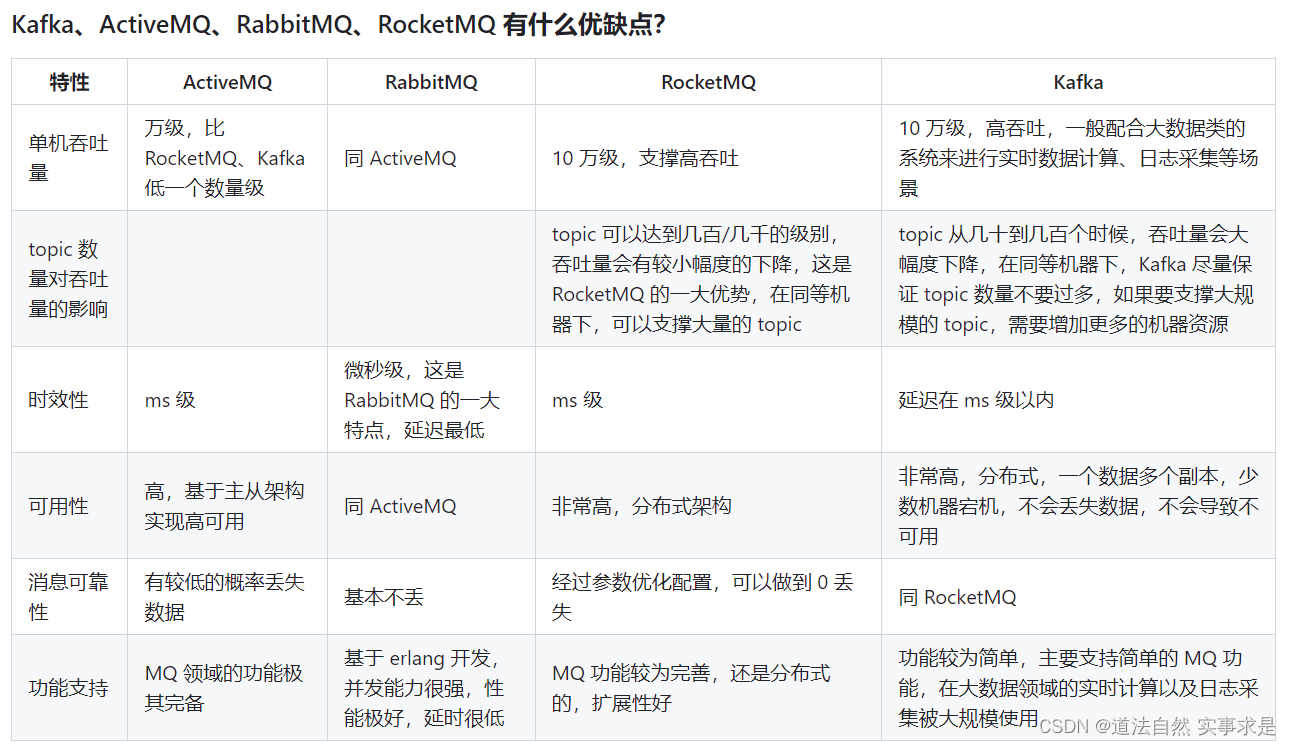
各中间件性能、优缺点对比
参考资料: Kafka、ActiveMQ、RabbitMQ、RocketMQ 有什么优缺点?...

修改表中某个字段等于另一个字段减去 2 小时的 SQL
需求:将表中到达时间按照客户要求改为比赛时间的提前 N 小时,具体如下: 表结构 update contestSchedule SET mainRefereeArrivalTimeDATE_FORMAT(CONCAT(2024-03-04 ,gameTime)- INTERVAL 2 HOUR, %H:%i), assistantRefereeArrivalTimeDAT…...
Jetpack Compose: Hello Android
Jetpack Compose 是一个现代化的工具包,用于使用声明式方法构建原生 Android UI。在本博文中,我们将深入了解一个基本的 “Hello Android” 示例,以帮助您开始使用 Jetpack Compose。我们将探讨所提供代码片段中使用的函数和注解。 入门 在…...
3月3号)
蓝桥每日一题 (差分)3月3号
//3279改变数组元素 自己做TLE:奈何想不出怎么用差分 #include<bits/stdc.h> using namespace std; //3279 改变数组元素(超时) const int N2e510; vector<int>a; int t,n; int main() {cin>>t;while(t--){cin>>n;…...
)
Mybatis和Spring Data Jpa的优缺点比较(八股文)
ORM(Object-Relational Mapping)框架是一种用于实现对象与关系数据库之间映射的工具或库。它可以将数据库中的表和记录映射成对象和属性,使开发人员可以使用面向对象的方式操作数据库,而不需要编写复杂的SQL语句。ORM框架的主要功…...

LeetCode买卖股票的最佳时机
LeetCode买卖股票的最佳时机 121 买卖股票的最佳时机Ⅰ 题目描述 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计…...
----->A. Entertainment in MAC)
Codeforces Round 932 (Div. 2)----->A. Entertainment in MAC
一,思路: 简单的字符串处理,当反转字符串后如果字典序减小了,那么肯定不会再执行反转操作,而是执行操作2,将反转后的字符串拼接(这样必定构造一个回文串),那么之后的操作…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
