路径规划 | 图解动态A*(D*)算法(附ROS C++/Python/Matlab仿真)
目录
- 0 专栏介绍
- 1 什么是D*算法?
- 2 D*算法核心概念一览
- 3 D*算法流程图
- 4 步步图解:算法实例
- 5 算法仿真与实现
- 5.1 ROS C++实现
- 5.2 Python实现
0 专栏介绍
🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);曲线优化(贝塞尔曲线、B样条曲线等)。
🚀详情:图解自动驾驶中的运动规划(Motion Planning),附几十种规划算法
1 什么是D*算法?
动态A*(Dynamic A*, D*)算法是一种增量式路径规划算法,与A*算法相比,它最大的优势是可以同时兼容静态环境和存在未知动态变化的场景,曾被美国用于火星探测器寻路。如果还不了解A*算法,可以看路径规划 | 图解A*、Dijkstra、GBFS算法的异同(附C++/Python/Matlab仿真)

这里有一个概念——增量式,什么是增量式呢?与启发式搜索利用启发函数指导高效搜索不同,增量式搜索对曾经的规划信息进行综合再利用以减少搜索范围和时间。
D*算法实现增量式规划采用从目标点向起始点的反向搜索策略:当既定路径被障碍阻塞时,障碍后各个节点到目标点的最短路径未被影响,只需在障碍附近重规划并更新起点到障碍处各节点的信息,当路径绕过障碍后即可重新利用曾经规划的到达目标位置的最短路径。
所以动态障碍越靠近起点,能重复利用的信息越多,规划效率越高。当动态障碍靠近终点时,仍要更新整张地图节点信息,相当于应用反向A*算法进行重规划。
2 D*算法核心概念一览
D*算法的核心概念如下所示:
-
c(x,y)c\left( x,y \right)c(x,y):从节点xxx移动到节点yyy的代价,若xxx、yyy间存在障碍则c(x,y)=infc\left( x,y \right) =\mathrm{inf}c(x,y)=inf;
-
t(x)t\left( x \right)t(x):节点xxx的表状态。有
NEW——未被搜索过的点OPEN——正在搜索的待考察节点CLOSED——被搜索过的节点。
为了适应动态环境,D*算法的
OPEN与CLOSED状态允许相互转化,当节点扩展后从开节点表中移除时,状态从OPEN变为CLOSED;当节点传播动态障碍信息给邻域时,节点将再次加入开节点表,状态从CLOSED变为OPEN -
h(x)h\left( x \right)h(x):从节点xxx到目标点的代价;
-
k(x)k\left( x \right)k(x):节点xxx的历史最小h(x)h\left( x \right)h(x)值,即
k(x)={h(x),t(x)=NEWmin{k(x),h(x)},otherwisek\left( x \right) =\begin{cases} h\left( x \right) \,\, , t\left( x \right) =\mathrm{NEW}\\ \min \left\{ k\left( x \right) ,h\left( x \right) \right\} , \mathrm{otherwise}\\\end{cases}k(x)={h(x),t(x)=NEWmin{k(x),h(x)},otherwise设置k(x)k\left( x \right)k(x)的目的在于加快障碍处局部路径重规划的效率。当某个路径点变为障碍时,其h(x)=infh\left( x \right) =\mathrm{inf}h(x)=inf而k(x)k\left( x \right)k(x)不变。若从开节点表中首选h(x)h\left( x \right)h(x)最小的点,则将最后考察障碍附近的点;而若从开节点表中首选k(x)k\left( x \right)k(x)最小的点,则将率先考察障碍附近的点,符合实际情况;
-
节点xxx的元状态:有
RAISED——此时k(x)<h(x)k\left( x \right) <h\left( x \right)k(x)<h(x)说明节点xxx受到障碍影响LOWER——此时k(x)=h(x)k\left( x \right) =h\left( x \right)k(x)=h(x)说明节点xxx未受障碍影响;
-
process_state()\mathrm{process}\_\mathrm{state}\left( \right)process_state():核心函数,静态环境下可以更新各节点到达目标点的最短路径及节点连接关系,动态环境下可以传播受障碍影响后节点h(x)h\left( x \right)h(x)的变更信息到邻域;
-
insert(x,val)\mathrm{insert}\left( x,val \right)insert(x,val):将节点xxx插入开节点表,并令其h(x)=valh\left( x \right) =valh(x)=val,更新k(x)k\left( x \right)k(x);
-
modify_cost(x)\mathrm{modify}\_\cos\mathrm{t}\left( x \right)modify_cost(x):通过insert(x,h(x)+c(x,x.parent))\mathrm{insert}\left( x,h\left( x \right) +c\left( x,x.\mathrm{parent} \right) \right)insert(x,h(x)+c(x,x.parent))将处于
CLOSED状态的节点xxx转换为OPEN状态
3 D*算法流程图
D*算法主函数流程如下所示

其中核心的process_state()\mathrm{process}\_\mathrm{state}\left( \right)process_state()算法流程如下

在将动态信息传播到邻域进行修正的过程中,分为两种情况讨论:
- 节点xxx处于
LOWER态。考虑到障碍的出现只可能让路径不变或更曲折,即让节点h(x)⩾k(x)h\left( x \right) \geqslant k\left( x \right)h(x)⩾k(x),所以对处在LOWER态的节点,不存在更优路径,此时只需将节点 的最优信息更新到邻域即可; - 节点xxx处于
RAISED态。与LOWER态节点不同,此时节点xxx处可能存在更优路径,即可能存在y∈neighbor(x)y\in \mathrm{neighbor}\left( x \right)y∈neighbor(x)使h(x)>h(y)+c(x,y)h\left( x \right) >h\left( y \right) +c\left( x,y \right)h(x)>h(y)+c(x,y)。对于y.parent=xy.\mathrm{parent}=xy.parent=x的情形RAISED态与LOWER态更新情况相同,以保持联结节点信息的同步。对于y.parent≠xy.\mathrm{parent}\ne xy.parent=x的情形,若h(y)>h(x)+c(x,y)h\left( y \right) >h\left( x \right) +c\left( x,y \right)h(y)>h(x)+c(x,y)则重新将节点xxx加入开节点表进行考察,因为xxx可能可以用更优的代价值来更新邻域;若h(x)>h(y)+c(x,y)h\left( x \right) >h\left( y \right) +c\left( x,y \right)h(x)>h(y)+c(x,y),考虑到h(y)⩽koldh\left( y \right) \leqslant k_{\mathrm{old}}h(y)⩽kold的情形在S2处已考虑,因此只需包含h(y)>koldh\left( y \right) >k_{\mathrm{old}}h(y)>kold,更进一步,由于节点yyy处在CLOSED状态,所以通常h(y)=k(y)⩽koldh\left( y \right) =k\left( y \right) \leqslant k_{\mathrm{old}}h(y)=k(y)⩽kold,但此处h(y)>koldh\left( y \right) >k_{\mathrm{old}}h(y)>kold说明节点yyy也受到了障碍影响导致价值升高,体现了将yyy重新纳入开节点表的必要性。
4 步步图解:算法实例
以下面的栅格地图为例,红色栅格表示起点,蓝色栅格表示终点,黄色栅格表示开节点表中的节点,绿色栅格表示闭节点表中的栅格

D*算法的静态规划阶段如下图所示

D*算法动态路径修正阶段如下所示

5 算法仿真与实现
5.1 ROS C++实现
double DStar::processState()
{if (open_list_.empty())return -1;double k_old = open_list_.begin()->first;DNodePtr x = open_list_.begin()->second;open_list_.erase(open_list_.begin());x->t = CLOSED;expand_.push_back(*x);std::vector<DNodePtr> neigbours;this->getNeighbours(x, neigbours);// RAISE state, try to reduce k value by neibhboursif (k_old < x->g_){for (DNodePtr y : neigbours){if (y->t != NEW && y->g_ <= k_old && x->g_ > y->g_ + this->getCost(y, x)){x->pid_ = y->id_;x->g_ = y->g_ + this->getCost(y, x);}}}// LOWER state, cost reductionsif (k_old == x->g_){for (DNodePtr y : neigbours){if (y->t == NEW || ((y->pid_ == x->id_) && (y->g_ != x->g_ + this->getCost(x, y))) ||((y->pid_ != x->id_) && (y->g_ > x->g_ + this->getCost(x, y)))){y->pid_ = x->id_;this->insert(y, x->g_ + this->getCost(x, y));}}}else{// RAISE statefor (DNodePtr y : neigbours){if (y->t == NEW || ((y->pid_ == x->id_) && (y->g_ != x->g_ + this->getCost(x, y)))){y->pid_ = x->id_;this->insert(y, x->g_ + this->getCost(x, y));}else if (y->pid_ != x->id_ && (y->g_ > x->g_ + this->getCost(x, y))){this->insert(x, x->g_);}else if (y->pid_ != x->id_ && (x->g_ > y->g_ + this->getCost(y, x)) && y->t == CLOSED && (y->g_ > k_old)){this->insert(y, y->g_);}}}return open_list_.begin()->first;
}

5.2 Python实现
def processState(self) -> float:# get node in OPEN set with min k valuenode = self.min_stateself.EXPAND.append(node)if node is None:return -1# record the min k value of this iterationk_old = self.min_k# move node from OPEN set to CLOSED setself.delete(node) # k_min < h[x] --> x: RAISE state (try to reduce k value by neighbor)if k_old < node.h:for node_n in self.getNeighbor(node):if node_n.h <= k_old and node.h > node_n.h + self.cost(node, node_n):# update h_value and choose parentnode.parent = node_n.currentnode.h = node_n.h + self.cost(node, node_n)# k_min >= h[x] -- > x: LOWER state (cost reductions)if k_old == node.h:for node_n in self.getNeighbor(node):if node_n.t == 'NEW' or \(node_n.parent == node.current and node_n.h != node.h + self.cost(node, node_n)) or \(node_n.parent != node.current and node_n.h > node.h + self.cost(node, node_n)):# Condition:# 1) t[node_n] == 'NEW': not visited# 2) node_n's parent: cost reduction# 3) node_n find a better parentnode_n.parent = node.currentself.insert(node_n, node.h + self.cost(node, node_n))else:for node_n in self.getNeighbor(node):if node_n.t == 'NEW' or \(node_n.parent == node.current and node_n.h != node.h + self.cost(node, node_n)):node_n.parent = node.currentself.insert(node_n, node.h + self.cost(node, node_n))else:if node_n.parent != node.current and \node_n.h > node.h + self.cost(node, node_n):self.insert(node, node.h)else:if node_n.parent != node.current and \node.h > node_n.h + self.cost(node, node_n) and \node_n.t == 'CLOSED' and \node_n.h > k_old:self.insert(node_n, node_n.h)return self.min_k

完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
相关文章:

路径规划 | 图解动态A*(D*)算法(附ROS C++/Python/Matlab仿真)
目录0 专栏介绍1 什么是D*算法?2 D*算法核心概念一览3 D*算法流程图4 步步图解:算法实例5 算法仿真与实现5.1 ROS C实现5.2 Python实现0 专栏介绍 🔥附C/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详…...
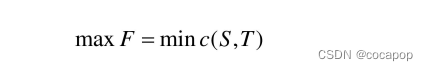
GraphCut、最大流最小割定理
G(V,E);V为点集,E为边集; 节点集V中的节点分为: (1)终端节点。不包含图像像素,用S和T表示。S为源点,T为汇点。图像分割中通常用S表示前景目标&a…...

Word文档的密码忘记了怎么办?
Word文档可以设置两种密码,文件的“限制密码”和“打开密码”,今天来分享一下忘记这两种密码可以如何处理。 如果忘记的是Word文档的“限制密码”,文档就无法编辑及更改了,菜单目录中的相关选项也都是灰色状态,无法点…...

Java分布式事务(二)
文章目录🔥分布式事务处理_认识本地事务🔥关系型数据库事务基础_并发事务带来的问题🔥关系型数据库事务基础_MySQL事务隔离级别🔥MySQL事务隔离级别_模拟异常发生之脏读🔥MySQL事务隔离级别_模拟异常发生之不可重复读&…...
游戏项目中的程序化生成(PCG):算法之外的问题与问题
本篇讨论的是什么 从概念上讲,PCG(程序化生成)的含义很广:任何通过规则计算得到的内容,都可算作是PCG。但在很多游戏项目的资料,包括本篇,讨论PCG时特指是:用一些算法/工具(特别是H…...
【C++】位图+哈希切割+布隆过滤器
文章目录一、位图1.1 位图概念1.2 位图实现1.2.1 把x对应比特位0置11.2.2 把x对应比特位1置01.2.1 查看x对应比特位1.3 位图源码1.4 位图的应用二、哈希切割(处理海量数据)三、布隆过滤器3.1 布隆过滤器的概念3.2 布隆过滤器的应用场景3.3 布隆过滤器的实…...
)
python实现网络游戏NPC任务脚本引擎(带限时任务功能)
python实现NPC任务脚本引擎 一、简介二、简单示例三、实现任务限时的功能四、结合twisted示例一、简介 要实现面向对象的网络游戏NPC任务脚本引擎,可以采用以下步骤: 1.定义NPC类:该类应该包括NPC的基本属性和行为,如名字、位置、血量、攻击力等等。NPC还应该有任务的列表…...
)
C语言的原子操作(待完善)
文章目录一、什么是原子操作二、为什么需要原子操作三、API一、什么是原子操作 原子操作是不可分割的,在执行完毕之前不会被任何其它任务或事件中断,可以视为最小的操作单元,是在执行的过程中、不会导致对数据的并发访问的、最小操作&#x…...

JavaScript Boolean 布尔对象
文章目录JavaScript Boolean 布尔对象Boolean 对象Boolean 对象属性Boolean 对象方法检查布尔对象是 true 还是 false创建 Boolean 对象JavaScript Boolean 布尔对象 Boolean(布尔)对象用于将非布尔值转换为布尔值(true 或者 false࿰…...
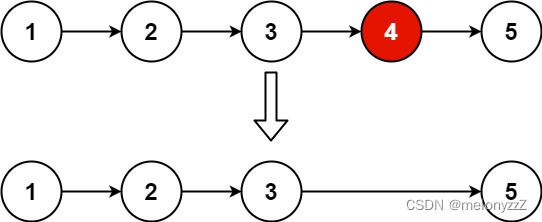
删除链表元素相关的练习
目录 一、移除链表元素 二、删除排序链表中的重复元素 三、删除排序链表中的重复元素 || 四、删除链表的倒数第 N 个结点 一、移除链表元素 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点,并返回 新的头…...

3DEXPERIENCE Works 成为了中科赛凌实现科技克隆环境的催化剂
您的企业是否想过实现设计数据的统筹管理,在设计上实现标准化,并把每位设计工程师串联起来协同办公?中科赛凌通过使用3DEXPERIENCE Works 实现了上述内容,一起来看本期案例分享吧!中科赛凌 通过其自主研发的单压缩机制冷技术实现零下190℃制…...

少儿编程 电子学会图形化编程等级考试Scratch一级真题解析(选择题)2022年12月
少儿编程 电子学会图形化编程等级考试Scratch一级真题解析2022年12月 选择题(共25题,每题2分,共50分) 1、小明想在开始表演之前向大家问好并做自我介绍,应运行下列哪个程序 A、 B、 C、 D、 答案:D...

【完整版】国内网络编译,Ambari 2.7.6 全部模块源码编译笔记
本次编译 ambari 2.7.6 没有使用科学上网的工具,使用的普通网络,可以编译成功,过程比 ambari 2.7.5 编译时要顺畅。 以下是笔记完整版。如果想单独查看本篇编译笔记,可参考:《Ambari 2.7.6 全部模块源码编译笔记》 该版本相对 2.7.5 版本以来,共有 26 个 contributors …...

HTML 颜色值
HTML 颜色值 颜色由红 (R)、绿 (G)、蓝 (B) 组成。 颜色值 颜色值由十六进制来表示红、绿、蓝(RGB)。 每个颜色的最低值为 0 (十六进制为 00 ),最高值为 255 (十六进制为 FF )。 十六进制值的写法为#号后跟三个或六个十六进制字符。 三位…...

RabbitMQ-消息的可靠性投递
文章目录0. 什么是消息的可靠性投递1. confirm机制2. return机制3. 总结0. 什么是消息的可靠性投递 在生产环境中,如果因为一些不明原因导致RabbitMQ重启,RabbitMQ重启过程中是无法接收消息的,那么我们就需要生产者重新发送消息。或者在消息…...
| 含思路)
华为OD机试题 - 最小叶子节点(JavaScript)| 含思路
华为OD机试题 最近更新的博客使用说明本篇题解:最小叶子节点题目输入输出示例一输入输出示例二输入输出Code解题思路华为OD其它语言版本最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD…...
)
嵌入式系统硬件设计与实践(开发过程)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 如果把电路设计看成是画板子的,这本身其实是狭隘了。嵌入式硬件设计其实是嵌入式系统中很重要的一个部分。里面软件做的什么样…...
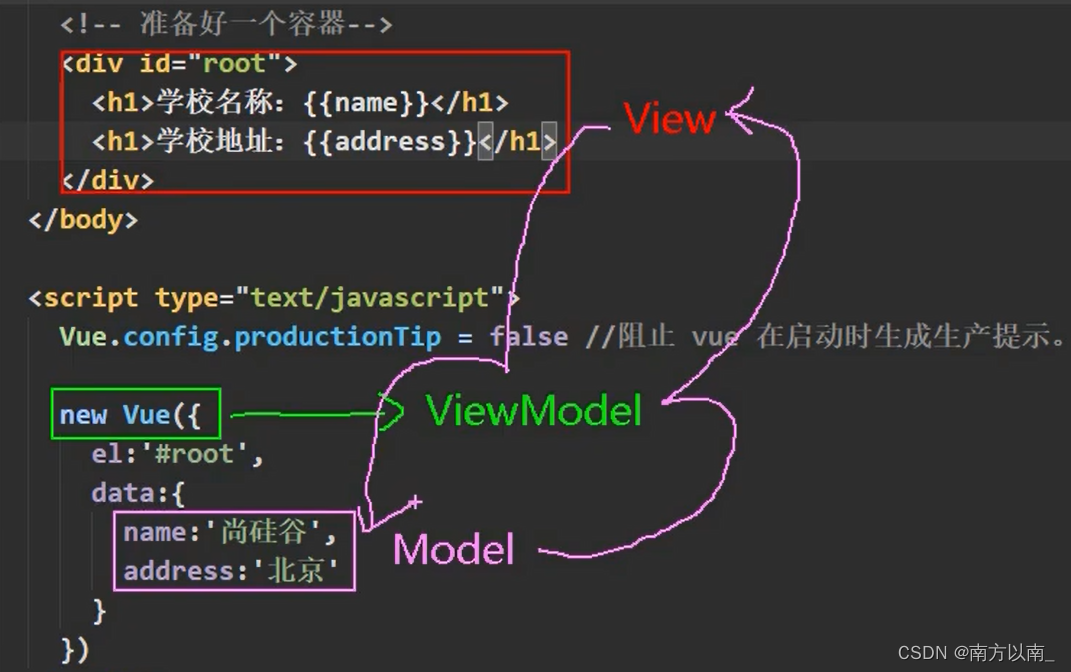
入门vue(1-10)
正确学习方式:视频->动手实操->压缩提取->记录表述 1基础结构 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"&…...

C#开发的OpenRA的游戏主界面怎么样创建3
继续游戏主界面创建的主题, 我们知道游戏的主界面上有很多部件,比如显示文本的标签(LabelWidget), 显示按钮(ButtonWidget)。那么这些部件又是如何创建在主界面上的呢? 其实这些部件是否显示,都是来源于文件yaml,在这里就是文件mainmenu.yaml, 在这个文件里定义了所有…...

秒懂算法 | 基于主成分分析法、随机森林算法和SVM算法的人脸识别问题
本文的任务与手写数字识别非常相似,都是基于图片的多分类任务,也都是有监督的。 01、数据集介绍与分析 ORL人脸数据集共包含40个不同人的400张图像,是在1992年4月至1994年4月期间由英国剑桥的Olivetti研究实验室创建。 此数据集下包含40个目录,每个目录下有10张图像,每个…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
