【深蓝学院】手写VIO第2章--IMU传感器--笔记
0. 内容

1. 旋转运动学
角速度的推导:
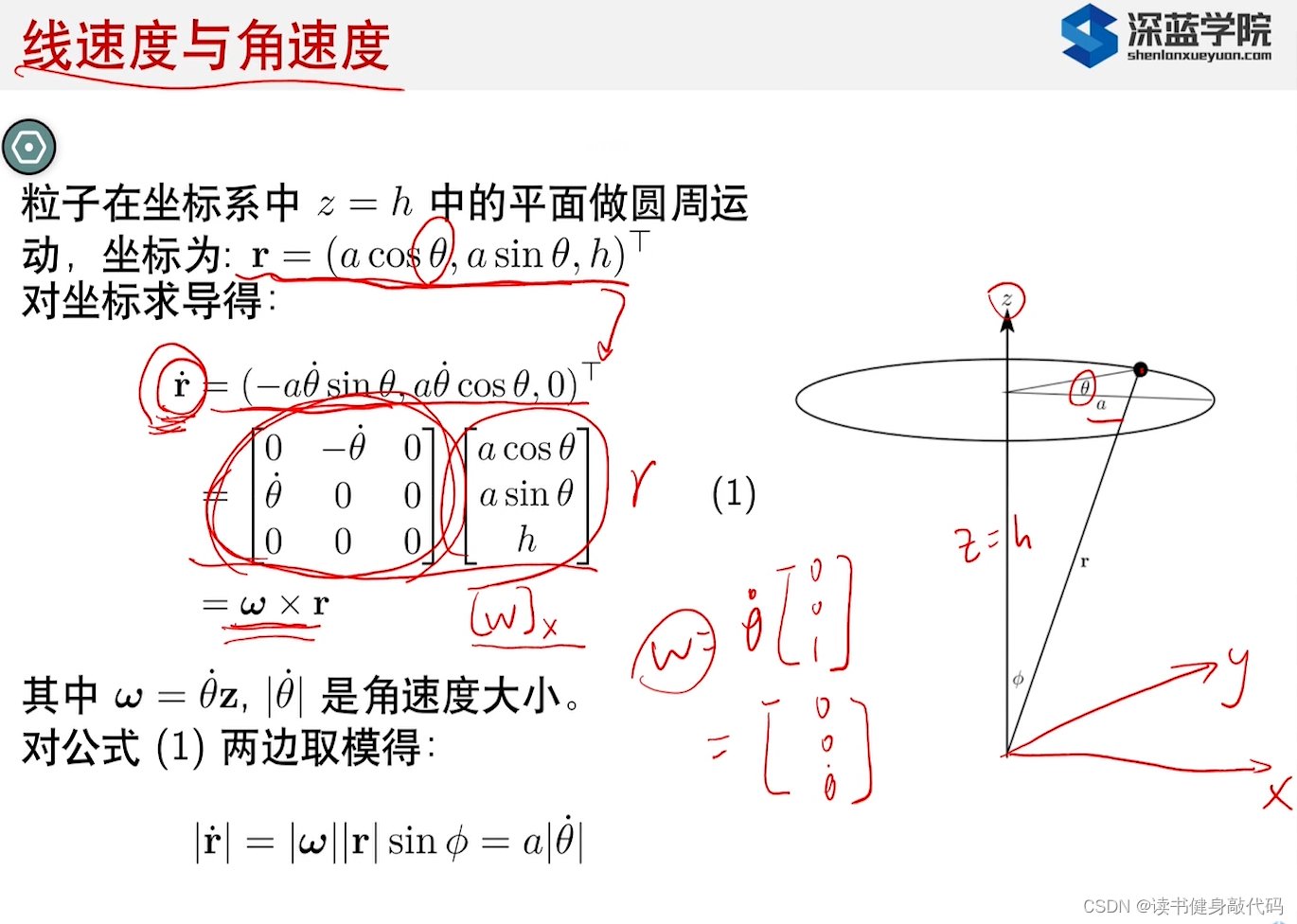
左=ω∧\omega^{\wedge}ω∧,而ω\omegaω是在z轴方向运动,=θ′[0,0,1]T\theta^{\prime}[0,0,1]^Tθ′[0,0,1]T
两边取模后得到结论: 线速度大小=半径 * 角速度大小
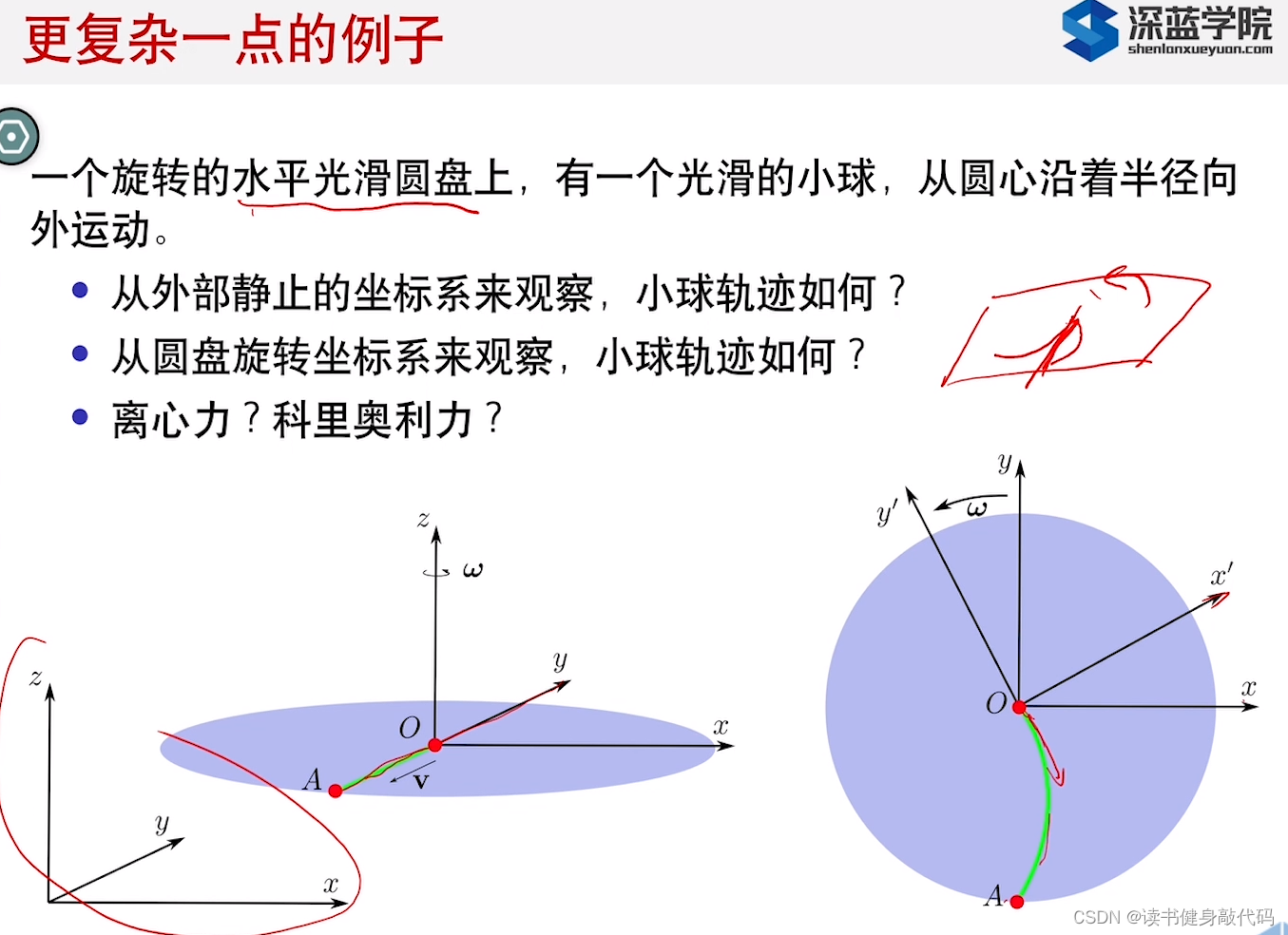

其中,对旋转矩阵求导根据第一章的结论:
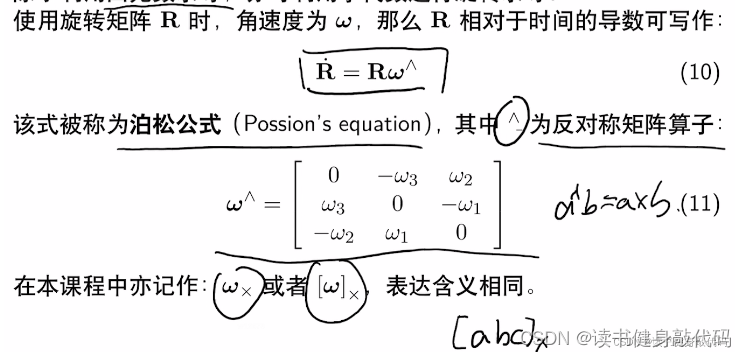
还有绿色箭头的公式,下面的推导看的不是很明白
实际上是把R的导数变成求极限的形式,但是这个极限怎么求的我不是很理解,然后就是下面这个公式
Rω∧=(Rω)∧RR\omega^\wedge=(R\omega)^\wedge RRω∧=(Rω)∧R


a=Rib∗aba = R_{ib}*a^ba=Rib∗ab表示body下的加速度在III系下的表示,仍是body下的加速度,只是表示在III系。
知道了这个科氏力之后,测量出科氏力以及运动的速度就能知道角速度了,这就是gyro的一个基本原理。
2. IMU测量模型及运动模型

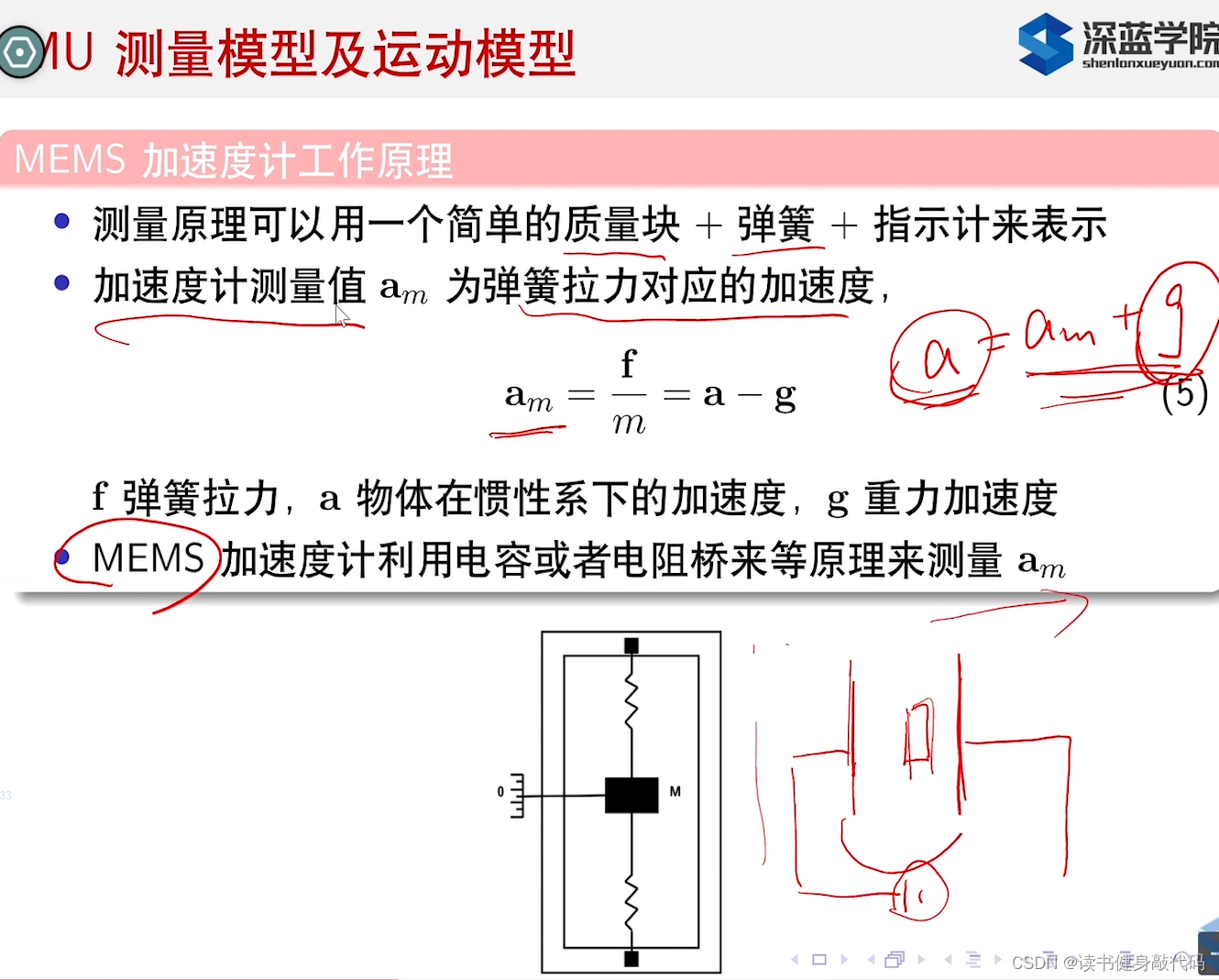
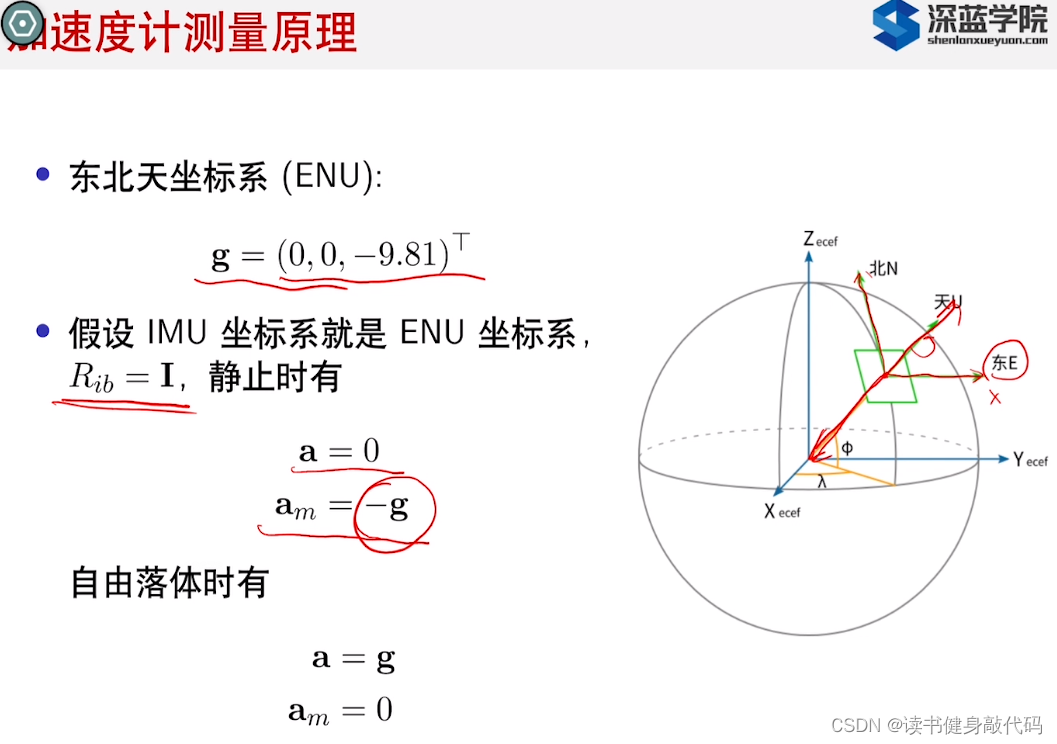

光纤陀螺仪一般较贵,原理是:光跑一圈路程是2πr2\pi r2πr,但如果在旋转,那就是2πr+x2\pi r+x2πr+x,测量出来这个x,用光速再进行相关计算就得到此时的角速度。
陀螺仪测角速度要两个轴:一个主动运动轴,一个敏感轴,敏感轴用于预测量科氏力
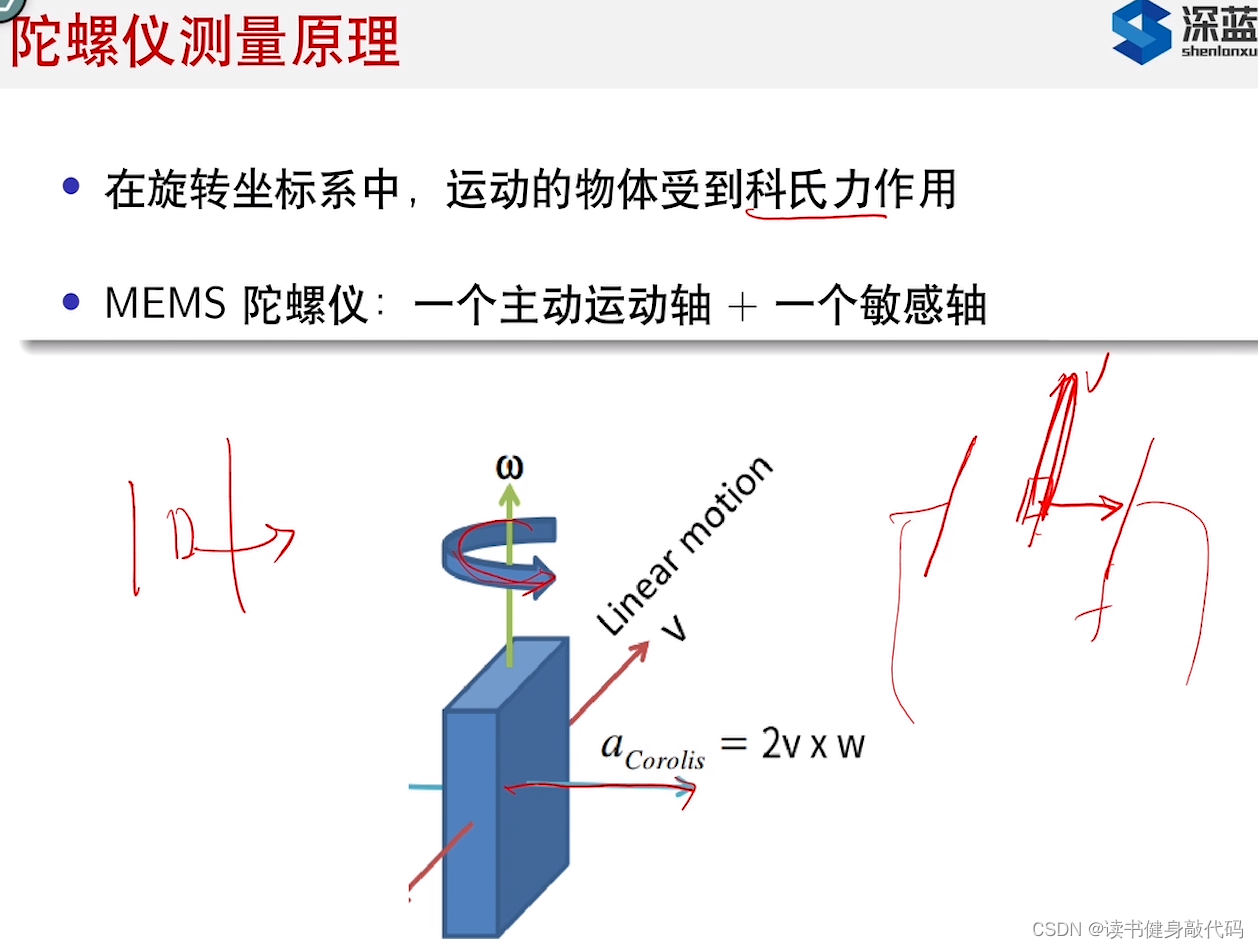
音叉振动陀螺
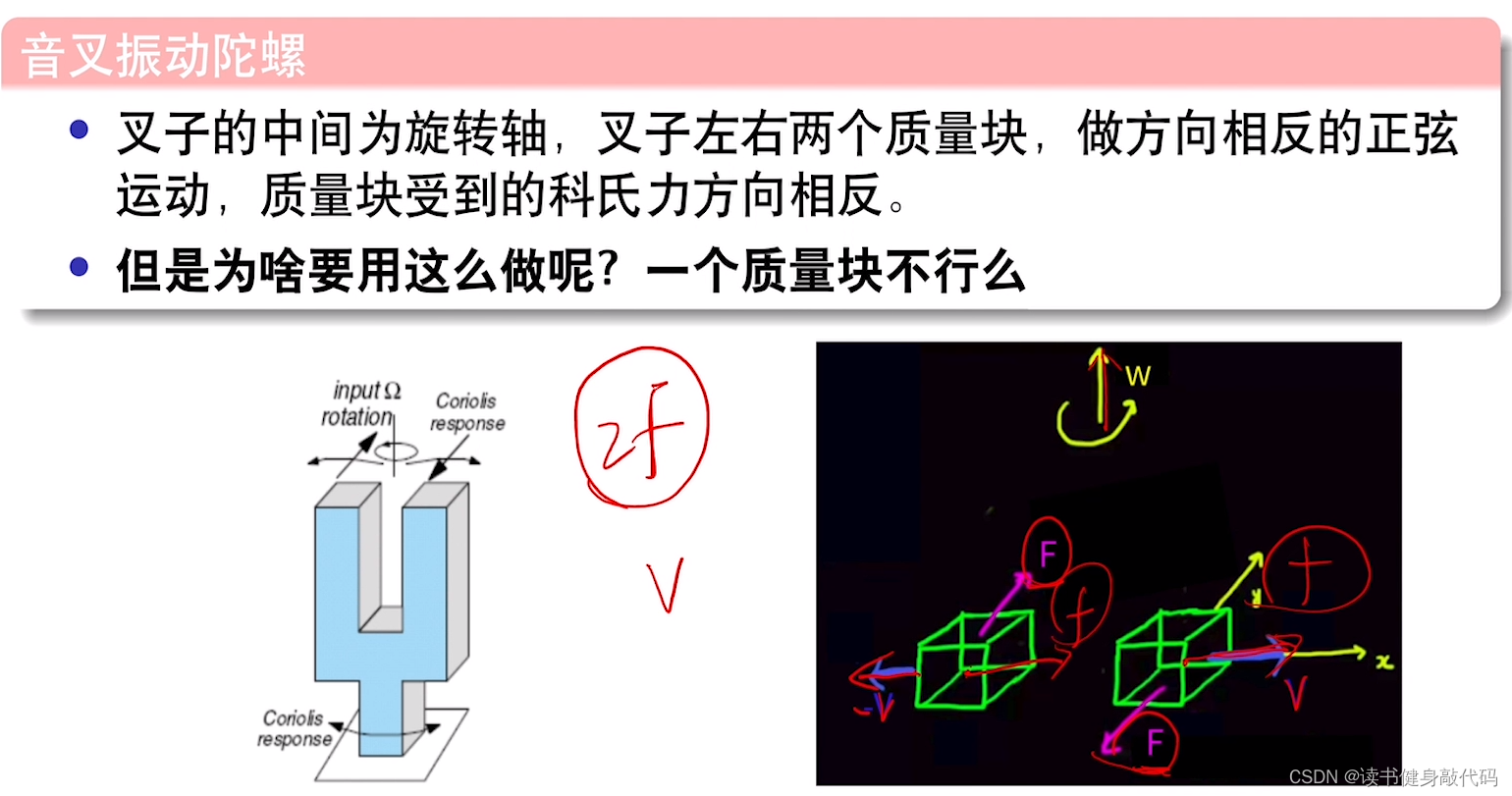
音叉两端左方向相反的正弦运动(什么叫正弦运动?音叉不是固定的吗? ),同一时刻其速度相反,±v,受到的科氏力大小相同方向相反F,整个音叉收到向右的力为f,左右也都为f,把受到的力相减,抵消之后,就能测出两倍科氏力2F,同时,知道自然块运动的速度,就能算出科氏力。
科氏力为2v∗ω2v*\omega2v∗ω,

这个G-sensitivity是灵敏度系数,比如机械振动会不会对IMU测量数据造成影响,如果不那么灵敏,就不会影响,如果比较灵敏,就需要考虑IMU减震等。
加速度计是否需要考虑科氏力影响?
不需要。

因为
1.即使开始加速时质量块会加速,但最终会达到平衡,速度v=0,最终的科氏力为0,
2.加计不是主动驱动的高速运动,会很缓慢地动,最终速度为0。
3. IMU误差模型
3.1 误差模型

3.2 确定性误差
确定性误差有bias和scale,
- bias随着时间会累积,使得位姿的误差perrp_{err}perr越来越大;
- scale可看成是原始物理v,ωv,\omegav,ω与ADC后的传感器输出值之间的比值,需要标定。
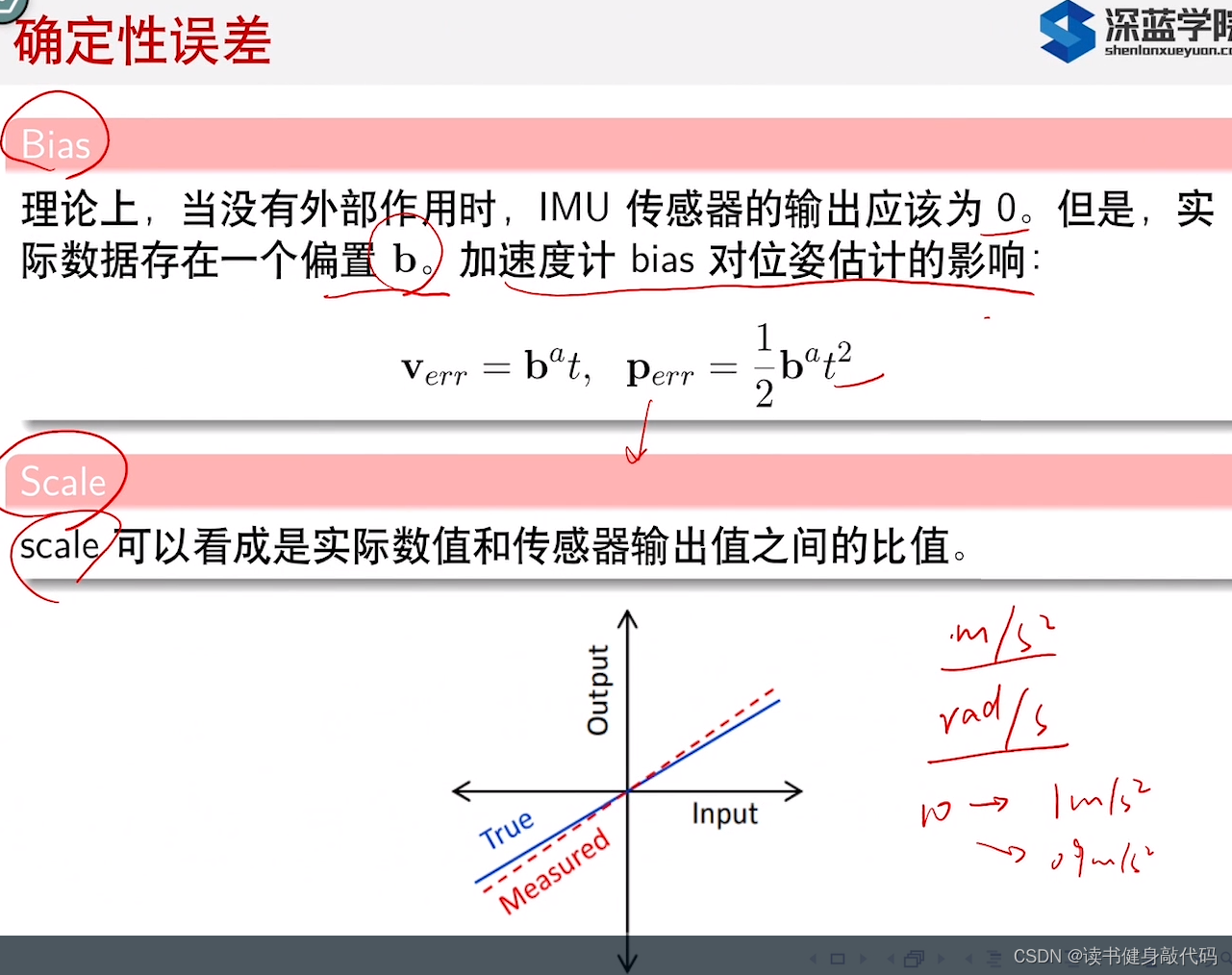
scale是尺度,Misalignment是轴偏,如yz轴投影到x轴上的轴偏。
不考虑bias时,测量出的lax=sxx∗ax+mxy∗ay+mxz∗azl_{ax}=s_{xx}*a_x + m_{xy}*a_y + m_{xz}*a_zlax=sxx∗ax+mxy∗ay+mxz∗az,尺度轴偏矩阵主对角线为尺度,其他为轴偏。

其他确定性误差还有
- 运行误差(每次都不一样),
- 温度相关误差(温度补偿或者标定方法)。
- 环境相关误差(高度,室内外等)

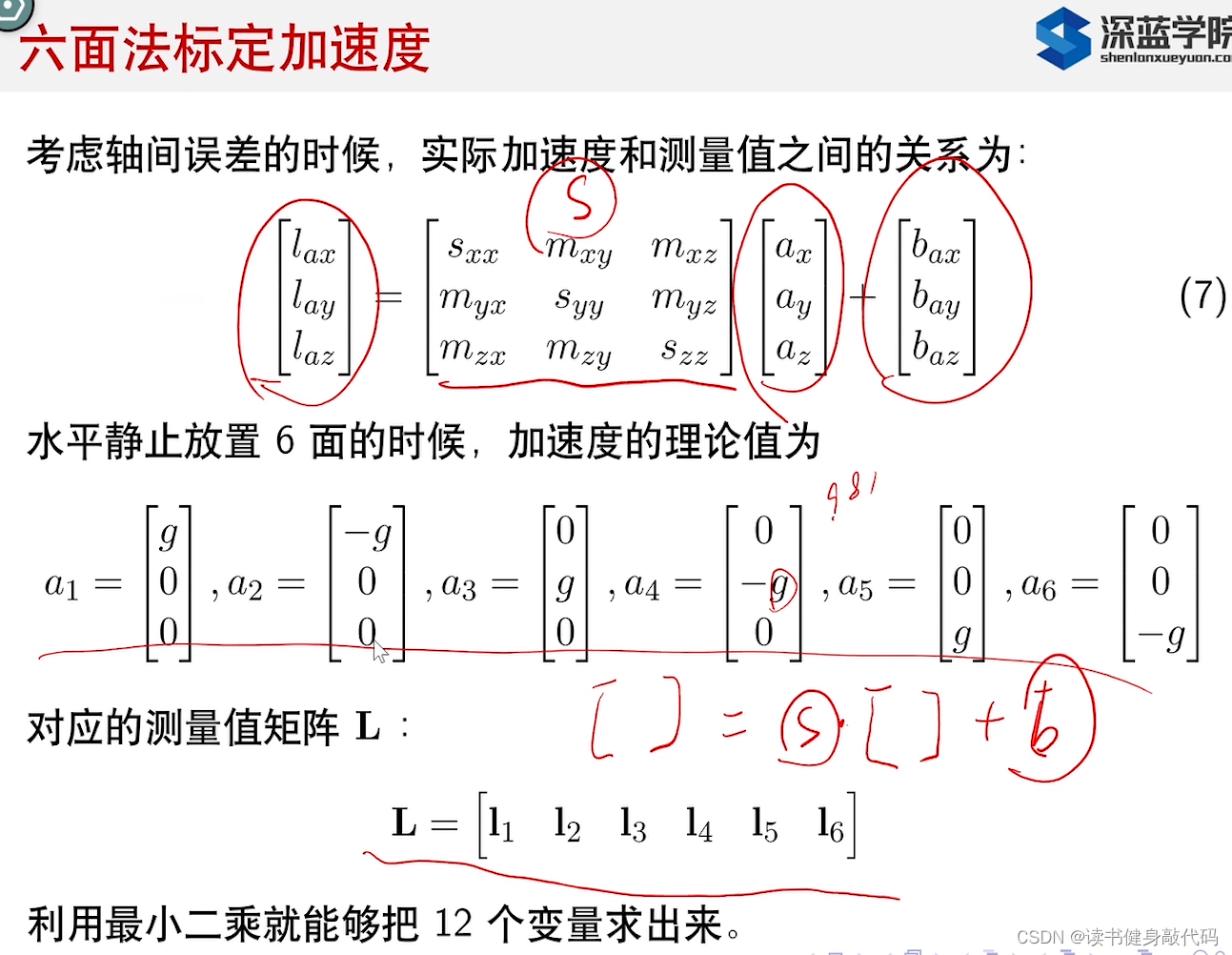
六面法标定bias和scale,分别将xzy三个轴朝上或者下放置,测出的应该是±g,但是会受到bias影响.于是b=lup+ldown2b = \frac{l^{up}+l^{down}}{2}b=2lup+ldown就是两倍bias的均值,反之,相减绝对值就是2g2g2g,一除就是尺度scale。
3.2.1 六面法标定acc

l1l_1l1 ~ l6l_6l6是加速度测量值,S,b是待标定的尺度轴偏矩阵和bias,a1a_1a1 ~ a6a_6a6是加速度的理论值,其中g=9.81g=9.81g=9.81是标量。如此可以标定出SSS和bbb。
L=S[a1,a2,a3,a4,a5,a6]+bL=S[a_1, a_2,a_3,a_4,a_5,a_6]+bL=S[a1,a2,a3,a4,a5,a6]+b
最小二乘法能够求出S和b共12个元素。
3.2.2 六面法标定gyro
同理,标定gyro也可以使用这种方法,需要有一个角速度较为精确的转台,也用6面,相对加计,此时我们知道较为精确的角速度ω1\omega_1ω1~ω6\omega_6ω6,即可标出gyro的尺度、轴偏、bias。

3.2.3 温度标定
一般采用soak method,精度较高。

3.3 IMU随机误差
3.3.1 IMU随机误差的介绍
bias的导数满足高斯分布n(t)n(t)n(t)(注意是导数而不是bias本身),这个bias的分布被称为随机游走(random walk)。

ADC采样时间段内认为数据是常数,采集的数据=理想数据+bias和随机游走的噪声带来的部分,这个不是常数,所以需要进行积分

仅考虑高斯白噪声时(假设bias和n(t)是相互独立的)的协方差计算推导:
这里的τ\tauτ实际上就是一个自变量,可以是x,y,zx,y,zx,y,z等任意一个,是因为ttt在这里要代表时间,所以使用了τ\tauτ作为这里的自变量。本身高斯白噪声是满足高斯分布n(t)n(t)n(t)的,就如(13)式所定义。
协方差相关补充:


方差是协方差的特殊情况,方差实际上是对自身的协方差,即D(X)=Cov(X,X)D(X)=Cov(X,X)D(X)=Cov(X,X),也就是X的二阶原点矩。
补充对于一二阶矩的定义:(一阶矩是期望E(X)E(X)E(X),二阶原点矩是E(X2)E(X^2)E(X2),二阶非原点矩E(((X−E(X))2)E(\quad((X-E(X))^2\quad)E(((X−E(X))2),平方是因为如果E(X)E(X)E(X)不为有0时,若出现了负值,则会使整体二阶矩偏大,如果加了平方就相当于加上了绝对值,就更能体现偏离均值的范围。

这里的协方差标准写法应该是Cov(nd2[k])Cov(n_d^2[k])Cov(nd2[k]),写法做了省略:Cov(nd[k],nd[k])=D(nd[k])=E(nd2[k])−E(nd[k])2=E(nd2[k])Cov(n_d[k],n_d[k])=D(n_d[k])=E(n_d^2[k])-E(n_d[k])^2=E(n_d^2[k])Cov(nd[k],nd[k])=D(nd[k])=E(nd2[k])−E(nd[k])2=E(nd2[k])(因为这里nd[k]n_d[k]nd[k]是均值为0的高斯分布,所以E(nd[k])=0\bm{E(n_d[k])=0}E(nd[k])=0,方差=平方的期望-期望的平方),不好理解,内部展开就是下面项目的相乘
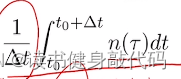

假设高斯白噪声是独立的,n(τ)n(t)n(\tau)n(t)n(τ)n(t)只有特定项(时间相差为1时)相乘才会有值,是狄拉克函数δ(t1−t2)=1(当且仅当t1−t2=1时)\delta(t_1-t_2)=1(当且仅当t_1-t_2=1时)δ(t1−t2)=1(当且仅当t1−t2=1时)
右因为前面有:

在tΔtt~\Delta tt Δt时间内只有一个时刻能使狄拉克函数为1,所以内层积分为1,外层积分为 (t+Δt)−Δt=Δt(t+\Delta t)-\Delta t=\Delta t(t+Δt)−Δt=Δt ,消掉分母即得协方差σ2Δt\frac{\sigma^2}{\Delta t}Δtσ2。
同理,下面的协方差写法也是做了省略,省略过程见上。

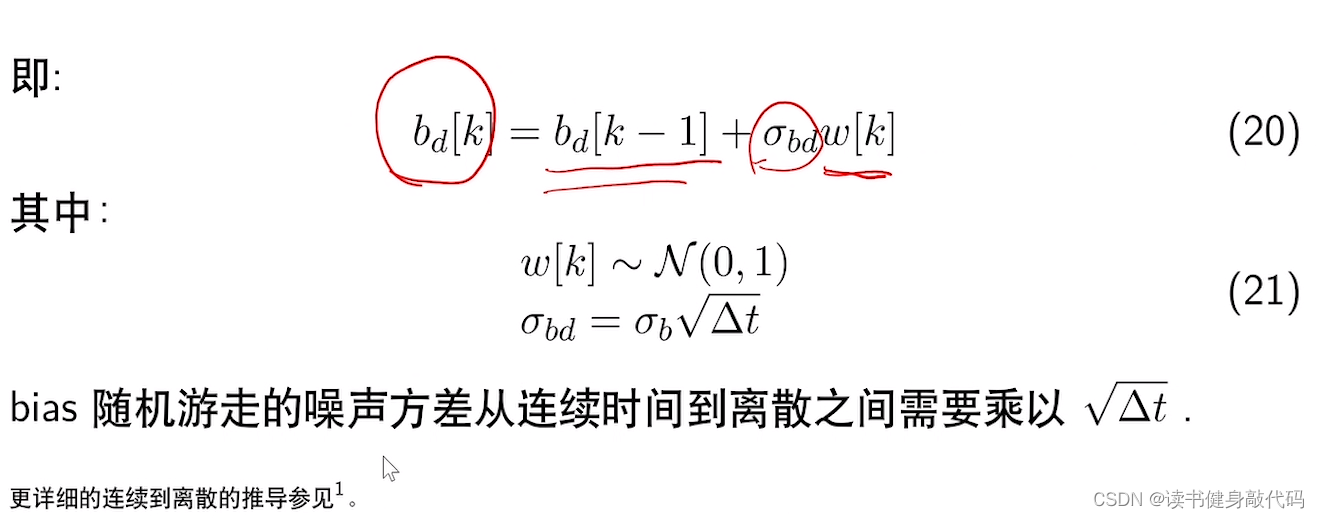
看起来像是开方的,σ\sigmaσ那一项相当于是服从一个N(0,1)N(0,1)N(0,1)分布。
结论:bias随即游走噪声方差从连续到离散之间需要∗Δt*\sqrt{\Delta t}∗Δt。(这个推导最后的开放有些看不懂,具体更详细的需要看论文

3.3.2 IMU随机误差的标定
主要是标定协方差,用于IMU选型,确定使用什么灵敏度类型的IMU
random walk noise的标定

艾伦方差的标定的论文:
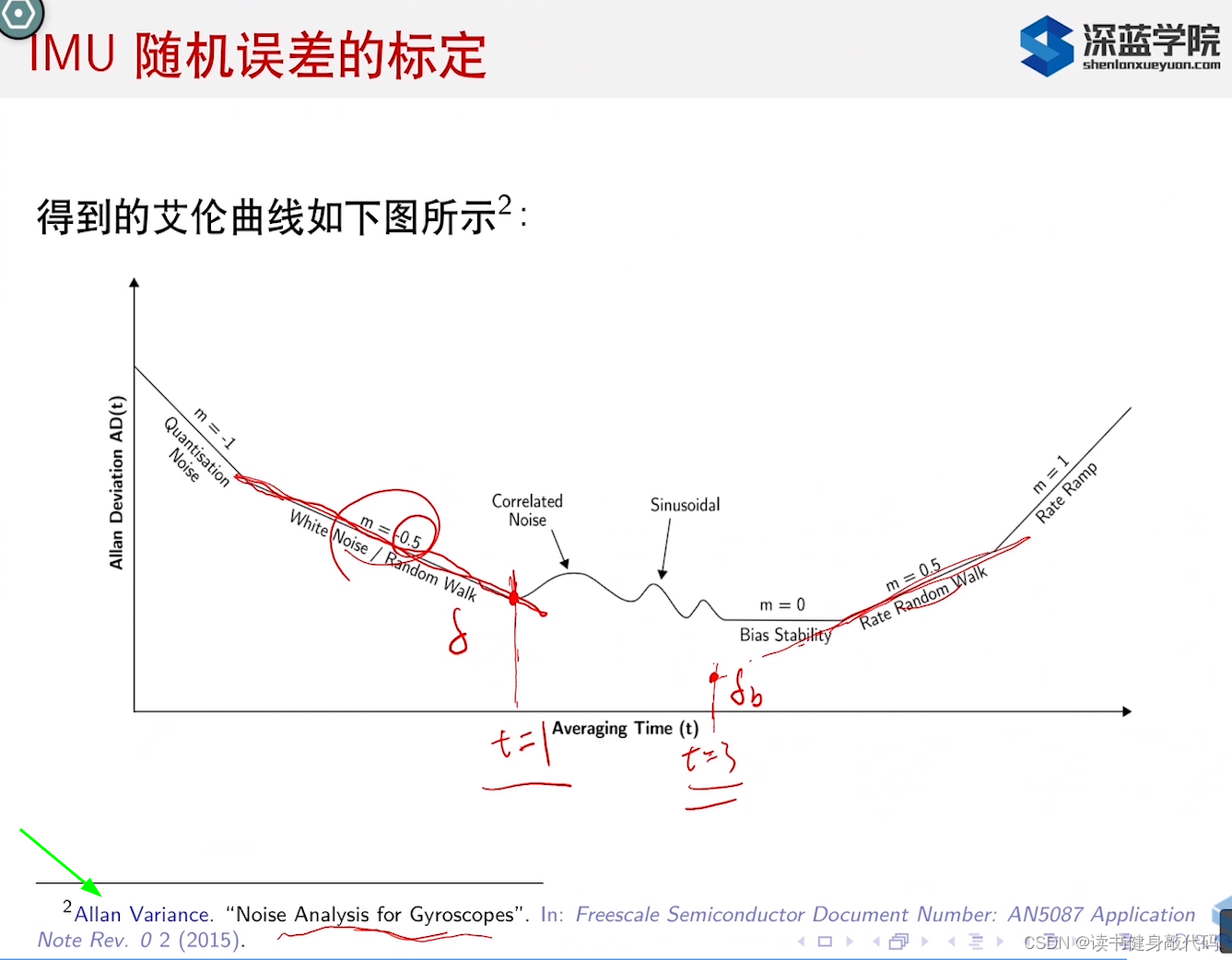
斜率-0.5处,t=1时的值是高斯白噪声方差的大小,斜率0.5,t=3处值是bias random walk的方差的大小,具体为什么,需要去看论文。(功率谱,靶向量?)
数据仿真部分:
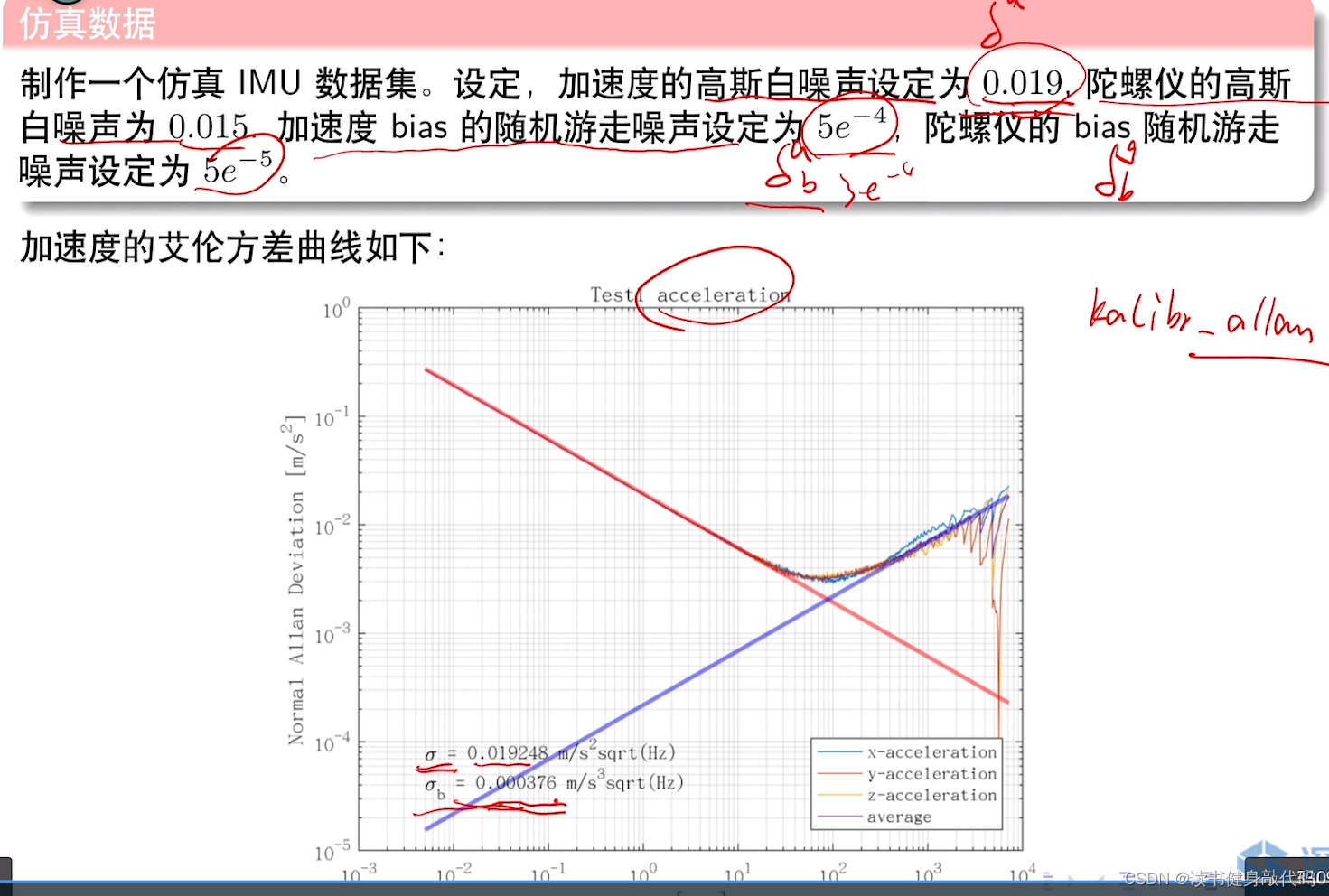 (主要是标定Acc和Gyro的bias的random walk的方差,使用Kalibr_allan)
(主要是标定Acc和Gyro的bias的random walk的方差,使用Kalibr_allan)
3.4 IMU数学模型
尺度因子如果标定的话会对精度有小幅提升(MSCKF什么黎明杨做的?VINS-MONO用过)
加计数学模型:加速度计的测量数据由尺度轴偏矩阵,重力分量,高斯白噪声,bias等构成。

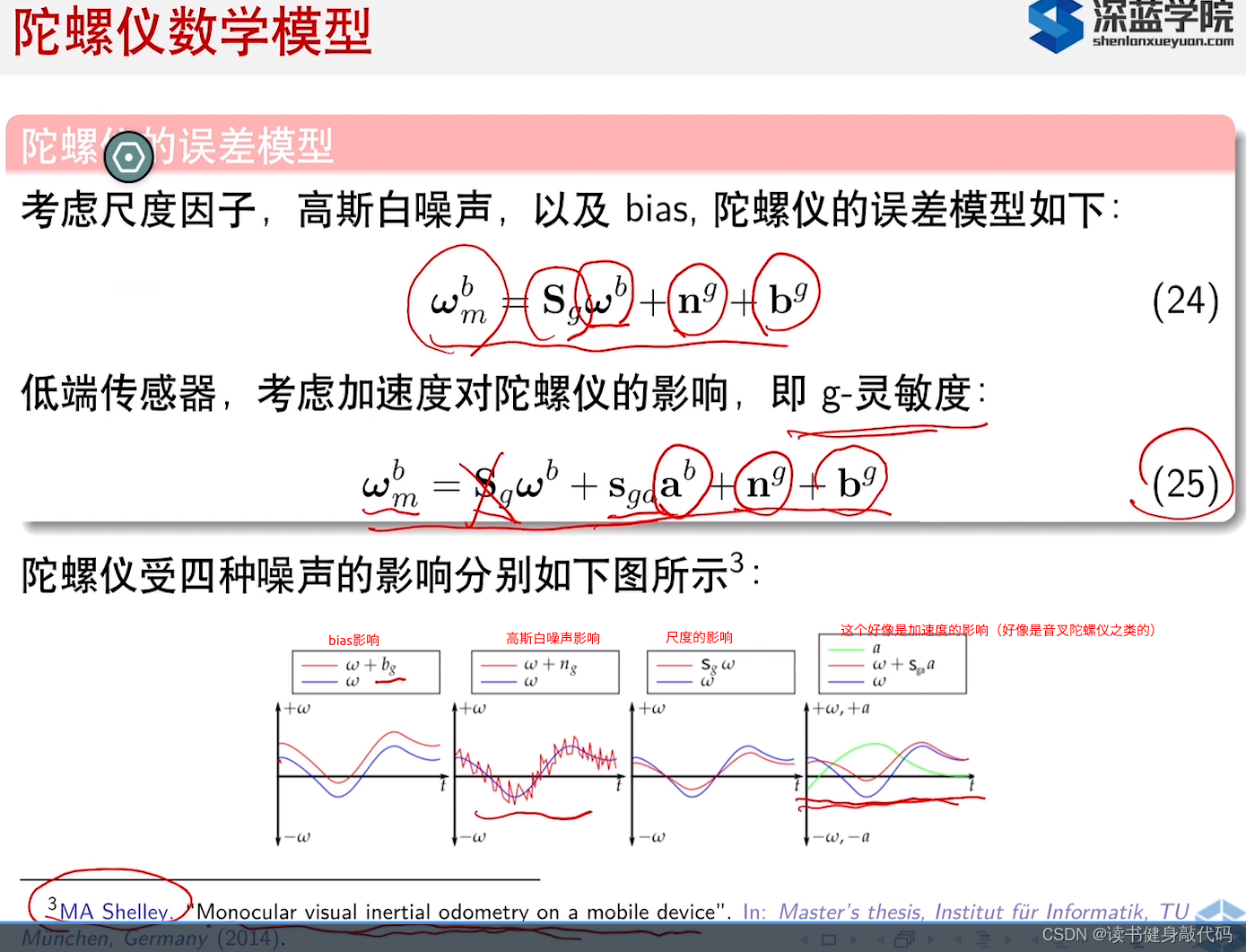
陀螺仪数学模型:
下面这篇论文对MSCKF进行了非常详细的建模,如果有兴趣可以看。
4. 运动模型离散时间处理:欧拉法&中值法
如何使用这些数据获得pose:
这里需要强调,重力加速度gwg^wgw前面的符号是跟坐标系定义有关的,如果是东北天,那就是-,如果是北东地就是+,整体上自洽即可。

基于导数,四元数导数的⊗\bm{\otimes}⊗是四元数乘法,可以积分计算位置,速度,旋转:

欧拉法进行近似,假设在每个积分间隔内,被积函数值保持不变,即k~k+1时刻的积分使用k时刻的值:

关于四元数的更新:
qωbk+1=qωbk+q′Δt=q⊗[10]+q⊗[012ωΔt](q提出来)=q⊗[112ωΔt]\begin{align} q_{\omega b_{k+1}} &= q_{\omega b_k}+q^{\prime}\Delta t \\ &=q \otimes \begin{bmatrix} 1 \\ 0 \end{bmatrix}+ q \otimes \begin{bmatrix} 0 \\ \frac{1}{2}\omega \Delta t \end{bmatrix} \\ (q提出来)&=q \otimes \begin{bmatrix} 1 \\ \frac{1}{2}\omega \Delta t \end{bmatrix} \\ \end{align} qωbk+1(q提出来)=qωbk+q′Δt=q⊗[10]+q⊗[021ωΔt]=q⊗[121ωΔt]
相较于欧拉法,中值法使用了k&k+1时刻的积分的均值,稍微准一点。
由于k->k+1时间较短,可以使用第k时刻的bias来矫正第k+1时刻的acc和gyro的值

5. IMU数据仿真
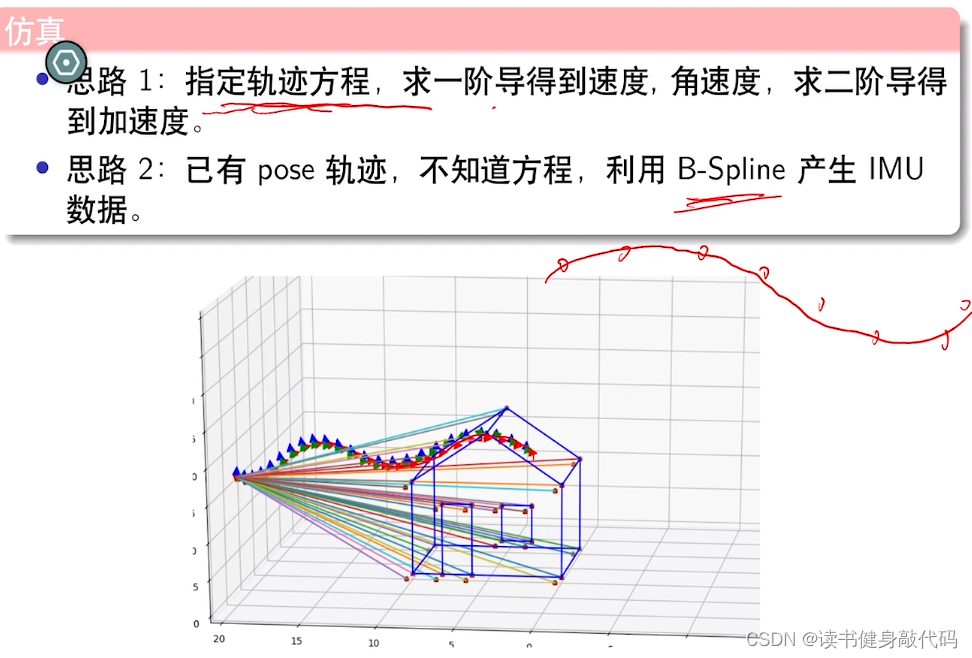
两种方式产生IMU仿真数据:
- 指定轨迹方程,求一阶导,二阶导得加速度等IMU仿真数据。
- 已有pose轨迹,但不知道方程,使用B-Spline产生IMU仿真数据。

由于四元数导数

所以四元数更新如上。
SO(3)更新也如上,更直观的方式是转换成欧拉角,需要将body系下的角速度转换为欧拉角速度。



粗略的理解:
旋转顺序是固定的(先绕哪个轴,再绕哪个轴)
最后转的x轴,所以x轴的角速度就是dψdt\frac{d\psi}{dt}dtdψ,
绕y轴转完之后还要绕x轴转个ψ\psiψ,所以y轴的角速度要乘一个R(ψ)R(\psi)R(ψ)
绕z轴转完之后还绕yx分别转了θ\thetaθ和ψ\psiψ,所以z方向的角速度要多乘个R(ψ)R(θ)R(\psi)R(\theta)R(ψ)R(θ)
所以就得到了Inertial->body系下的角速度转换矩阵,求逆就得从body->Inernial下的转换。

6. 作业

Reference
1. MSCKF详细建模推导(国外硕士论文)

2. Allan方差曲线论文

3. 离散和连续的IMU随机误差方差推导

4. 6面法标定误差(自己之前看过abstract的)
2014 ICRA:A Robust and Easy to Implement Method for IMU Calibration without
External Equipments
5. IMU数据仿真时IMU body系下的角速度转化为欧拉角速度课件

6. 利用B Spline(B样条)和已有IMU数据你拟合方程,产生IMU数据

相关文章:

【深蓝学院】手写VIO第2章--IMU传感器--笔记
0. 内容 1. 旋转运动学 角速度的推导: 左ω∧\omega^{\wedge}ω∧,而ω\omegaω是在z轴方向运动,θ′[0,0,1]T\theta^{\prime}[0,0,1]^Tθ′[0,0,1]T 两边取模后得到结论: 线速度大小半径 * 角速度大小 其中,对旋转矩…...
网络基础(二)之HTTP与HTTPS
应用层 再谈 "协议" 协议是一种 "约定". socket api的接口, 在读写数据时, 都是按 "字符串" 的方式来发送接收的. 如果我们要传输一些"结构化的数据" 怎么办呢? 为什么要转换呢? 如果我们将struct message里面的信息…...

Python每日一练(20230306)
目录 1. 翻转二叉树 ★★ 2. 最长公共前缀 ★★ 3. 2的幂 ★ 1. 翻转二叉树 翻转一棵二叉树。 示例 1: 输入: 4/ \2 7/ \ / \ 1 3 6 9 输出: 4/ \7 2/ \ / \ 9 6 3 1示例 2: 输入: 1…...

C/C++每日一练(20230305)
目录 1. 整数分解 ☆ 2. 二叉树的最小深度 ★★ 3. 找x ★★ 1. 整数分解 输入一个正整数,将其按7进制位分解为各乘式的累加和。 示例 1: 输入:49 输出:497^2示例 2: 输入:720 输出:720…...

SAS字典的应用
数据字典中常用信息检索DICTIONARY.COLUMNS、DICTIONARY.TABLES以及DICTIONARY.MEMBERS等字典表的内容。在编程实践中,如何以SAS字典表来提高效率。 1、DICTIONARY.COLUMNS 对于当前SAS任务的全部数据集,表格DICTIONARY.COLUMNS包含了诸如变量的名称、类…...

Mysql中的函数和触发器
函数函数是什么?多用于查询语句,实现了某种功能;用途与存储过程不同,但语法是类似的;函数语法create function 函数名([参数列表]) returns 数据类型 begin DECLARE 变量; sql 语句; return 值; end; 设置函…...

分布式架构之(Zookeeper原理)
Zookeeper是一个典型的分布式数据一致性的结局方案,分布式应用程序可以基于它实现注入数据发布、订阅、负载均衡、命名服务、分布式协调/通知、集群管理、Master选举、分布式锁和分布式队列等功能, Zookeeper可以保证如下分布式一致性特性: 顺…...

Java框架学习 | MyBatis
问题导向学习MyBatis 为什么要有MyBatis框架? 避免Java开发者直接使用 JDBC重复做数据库操作,同时更便捷地实现想要的数据库相关功能,让Java专注于开发业务。 MyBatis框架如何实现该目的? MyBatis是半自动化持久层ORM框架&#x…...
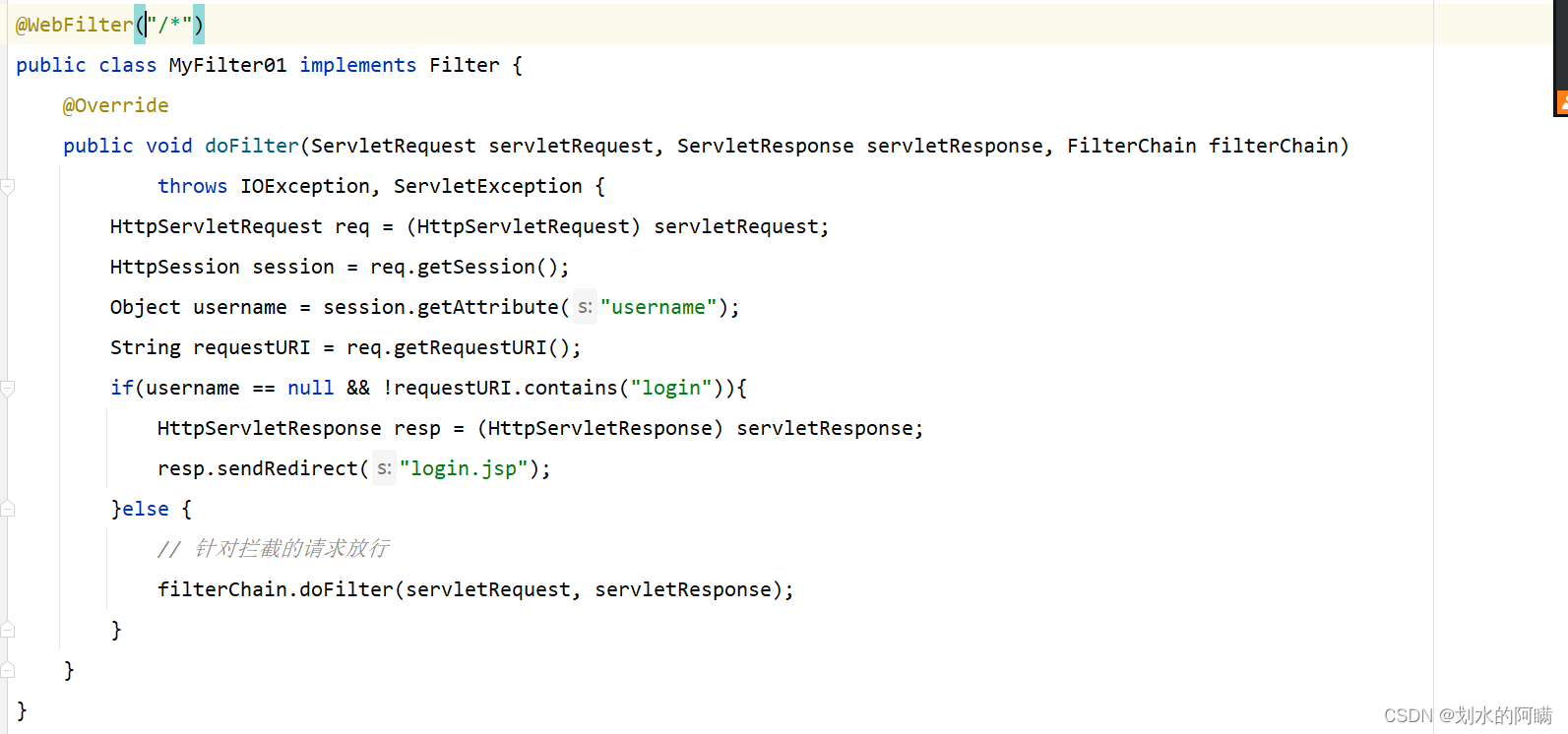
Cookie+Session详解
文章目录批量删除会话技术简介CookieCookie 查看Cookie 的删除Cookie 使用页面获取 cookie 信息cookie 特点Sessionsession 的使用Session 登录权限验证过滤器简介过滤器的使用WebFilter 注解过滤放行登录权限验证批量删除 servlet 类 dao 层 会话技术 简介 在计算机领域…...

CAPL脚本要注意区分elcount和strlen求数组长度的区别,不然要吃大亏
🍅 我是蚂蚁小兵,专注于车载诊断领域,尤其擅长于对CANoe工具的使用🍅 寻找组织 ,答疑解惑,摸鱼聊天,博客源码,点击加入👉【相亲相爱一家人】🍅 玩转CANoe&…...

CSS常用选择器
目录 1.CSS是什么 2.CSS的三种写法 2.1内部样式 2.2内联样式 2.3外部样式 3.CSS选择器 3.1标签选择器 3.2类选择器(更好的选择) 3.3ID选择器 3.4后代选择器 3.5子选择器 3.6并集选择器 3.7伪类选择器(复合选择器的特殊用法) 1.CSS是什么 CSS全称Cascding Style Sh…...

Registry与DGC的攻击利用
0x01 2022-02-03写的一篇文章。 0x02 Registry Registry指的是RMI的注册表,攻击的目标是注册表所在的机器,一般注册表和RMI Server在同一个机器上,特殊情况下也会在不同机器上。 在我们通过LocateRegistry#getRegistry获取到目标开启的注…...

赛道持续降温!又一家自动驾驶公司裁员,市值曾超50亿美元
从去年下半年开始,自动驾驶赛道的裁员、倒闭风潮盛行。 本周,美股卡车自动驾驶上市公司Embark Trucks(EMBK)宣布将裁员70%,同时大幅缩减业务。“痛苦可能还没有结束,”公司首席执行官Alex Rodrigues在给员…...

路径规划 | 图解动态A*(D*)算法(附ROS C++/Python/Matlab仿真)
目录0 专栏介绍1 什么是D*算法?2 D*算法核心概念一览3 D*算法流程图4 步步图解:算法实例5 算法仿真与实现5.1 ROS C实现5.2 Python实现0 专栏介绍 🔥附C/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详…...
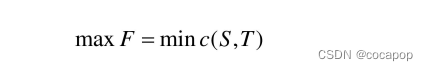
GraphCut、最大流最小割定理
G(V,E);V为点集,E为边集; 节点集V中的节点分为: (1)终端节点。不包含图像像素,用S和T表示。S为源点,T为汇点。图像分割中通常用S表示前景目标&a…...

Word文档的密码忘记了怎么办?
Word文档可以设置两种密码,文件的“限制密码”和“打开密码”,今天来分享一下忘记这两种密码可以如何处理。 如果忘记的是Word文档的“限制密码”,文档就无法编辑及更改了,菜单目录中的相关选项也都是灰色状态,无法点…...

Java分布式事务(二)
文章目录🔥分布式事务处理_认识本地事务🔥关系型数据库事务基础_并发事务带来的问题🔥关系型数据库事务基础_MySQL事务隔离级别🔥MySQL事务隔离级别_模拟异常发生之脏读🔥MySQL事务隔离级别_模拟异常发生之不可重复读&…...
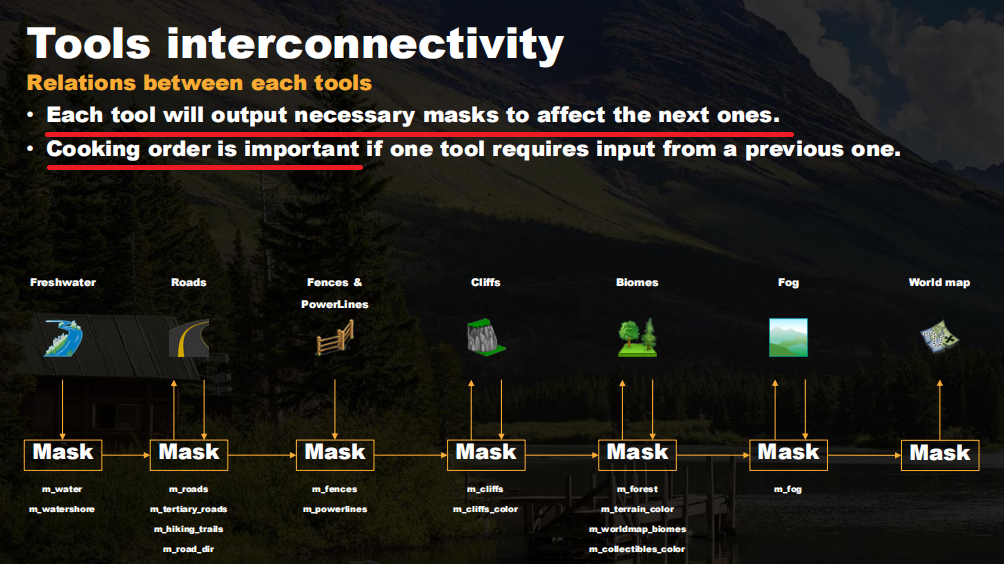
游戏项目中的程序化生成(PCG):算法之外的问题与问题
本篇讨论的是什么 从概念上讲,PCG(程序化生成)的含义很广:任何通过规则计算得到的内容,都可算作是PCG。但在很多游戏项目的资料,包括本篇,讨论PCG时特指是:用一些算法/工具(特别是H…...
【C++】位图+哈希切割+布隆过滤器
文章目录一、位图1.1 位图概念1.2 位图实现1.2.1 把x对应比特位0置11.2.2 把x对应比特位1置01.2.1 查看x对应比特位1.3 位图源码1.4 位图的应用二、哈希切割(处理海量数据)三、布隆过滤器3.1 布隆过滤器的概念3.2 布隆过滤器的应用场景3.3 布隆过滤器的实…...
)
python实现网络游戏NPC任务脚本引擎(带限时任务功能)
python实现NPC任务脚本引擎 一、简介二、简单示例三、实现任务限时的功能四、结合twisted示例一、简介 要实现面向对象的网络游戏NPC任务脚本引擎,可以采用以下步骤: 1.定义NPC类:该类应该包括NPC的基本属性和行为,如名字、位置、血量、攻击力等等。NPC还应该有任务的列表…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
