算法简单试题
一、选择题
01.一个算法应该是( B ).
A.程序 B.问题求解步骤的描述
C.要满足五个基本特性 D.A和C
02.某算法的时间复杂度为O(n²),则表示该算法的( C )。
A,问题规模是n² (默认都是n) B.执行时间等于n² <=k*n²
C.执行时间与n²成正比 D.问题规模与n²成正比
解析:算法时间复杂度:O(F(n))意味着算法在任何情况下,规模为n时,所花费的时间<=k*F(n)
03.若某算法的空间复杂度为O(1),则表示该算法( B )。
A,不需要任何辅助空间 B.所需辅助空间大小与问题规模n无关
C.不需要任何空间 D.所需空间大小与问题规模n无关
04.下列关于时间复杂度的函数中,时间复杂度最小的是( D ).
05.以下算法的时间复杂度为( D ).
void fun(int n){ //n作为参数
int i=1;while(i<=n)
i=i*2; //核心运算}
![]()
解析:核心操作是i=i*2;判断运算次数 ,即1*2*2*2乘多少次是n (2的几次方是n)
06.有以下算法,其时间复杂度为( C ).
void fun (int n){
int i=0;
while(i*i*i<=n)
i++; //i通过++操作往后推进,是核心操作}
![]()
解析:核心运算是i++,i*i*i仅用于逻辑判断,并没有“推进i”
当i*i*i>n时,则停止增加 即i = n开三次方
07.程序段如下:
for(i=n-1;i>1;i--)
for(j=1;j<i;j++)
if(A[j]>A[j+1]) //满足条件执行if
A[j]与A[j+1]对换;
其中n为正整数,则最后一行语句的频度在最坏情况下是( D )。![]()
解析:冒泡排序的算法代码,所有相邻元素都为逆序时,最后一行的语句每次都会执行
08.下列程序段的时间复杂度为( A )。
if(n>=0){
for (int i=0;i<n;i++)
for(int j=0;j<n;j++)
printf("输入数据大于或等于零\n");
}
else{
for(int j=0;j<n;j++)
printf("输入数据小于零\n");
![]()
09.以下算法中加下画线的语句的执行次数为( A )。 m++的执行次数
int m=0,i,j;
for(i=1;i<=n;i++)
for(j=1;j<=2*i;j++)
m++;
A. n(n+1) B.n C. n+1 D. n²
10.下列函数代码的时间复杂度是( C )。
int Func(int n){
if(n==1)return 1;
elsereturn 2* Func(n/2)+n;
![]()
11.【2011统考真题】设n是描述问题规模的非负整数,下列程序段的时间复杂度是( A )
x=2; //初值
while(x<n/2) //结束条件x=2*x; //执行操作
![]()
解析:x=2*2*2*....乘多少次2达到n
12.【2012统考真题】求整数n(n≥0)的阶乘的算法如下,其时间复杂度是( B )。
int fact(int n){
if(n<=1)return 1;
return n*fact (n-1); //递归程序
![]() “
“
解析:程序就是一个递归,整个程序的基础操作只有递归处有乘法,一次递归是一次乘法运算,值为n的情况下递归嵌套n次
13.【2014统考真题】下列程序段的时间复杂度是( C )。
count=0;
for(k=1;k<=n;k*=2)for(j=1;j<=n;j++)
count++;
![]()
解析:第一层:k的取值分别是1,2,4,8...一直到n:log2n次循环
第二层:无论k的取值是多少,第二层都是自加n次
14.【2017统考真题】下列函数的时间复杂度是( B ).
int func (int n){
int i=0,sum=0;
while(sum<n)sum += ++i;
return i;
)
![]()
解析:核心操作:sum+=++i; sum的变化过程:0+1+2+3....+i ,当sum<n时跳出循环,判断i加了几次,求和公式为sum=i*(i-1)/2<n,根据数量级可以把左边看成i²,即i²<n ,所以i=n的二分之一次方
15.【2019统考真题】设n是描述问题规模的非负整数,下列程序段的时间复杂度是( B )。
x=0;
while (n>=(x+1)*(x+1))x=x+1;
![]()
解析:(x+1)²<=n ,根据同阶数量级可以看成x²<n 即x趋向于根号n
16.【2022统考真题】下列程序段的时间复杂度是( B )。
int sum=0;
for(int i=l;i<n;i*=2)
for(int j=0;j<i;j++)
sum++;
![]()
解析:求出sum++的执行次数
第一层:i=1,2,4,8...2的k次方
第二层:j<i,所以j有0~i-1个
1+2+3+....+2的k次方 = 2的k+1次方-1<2n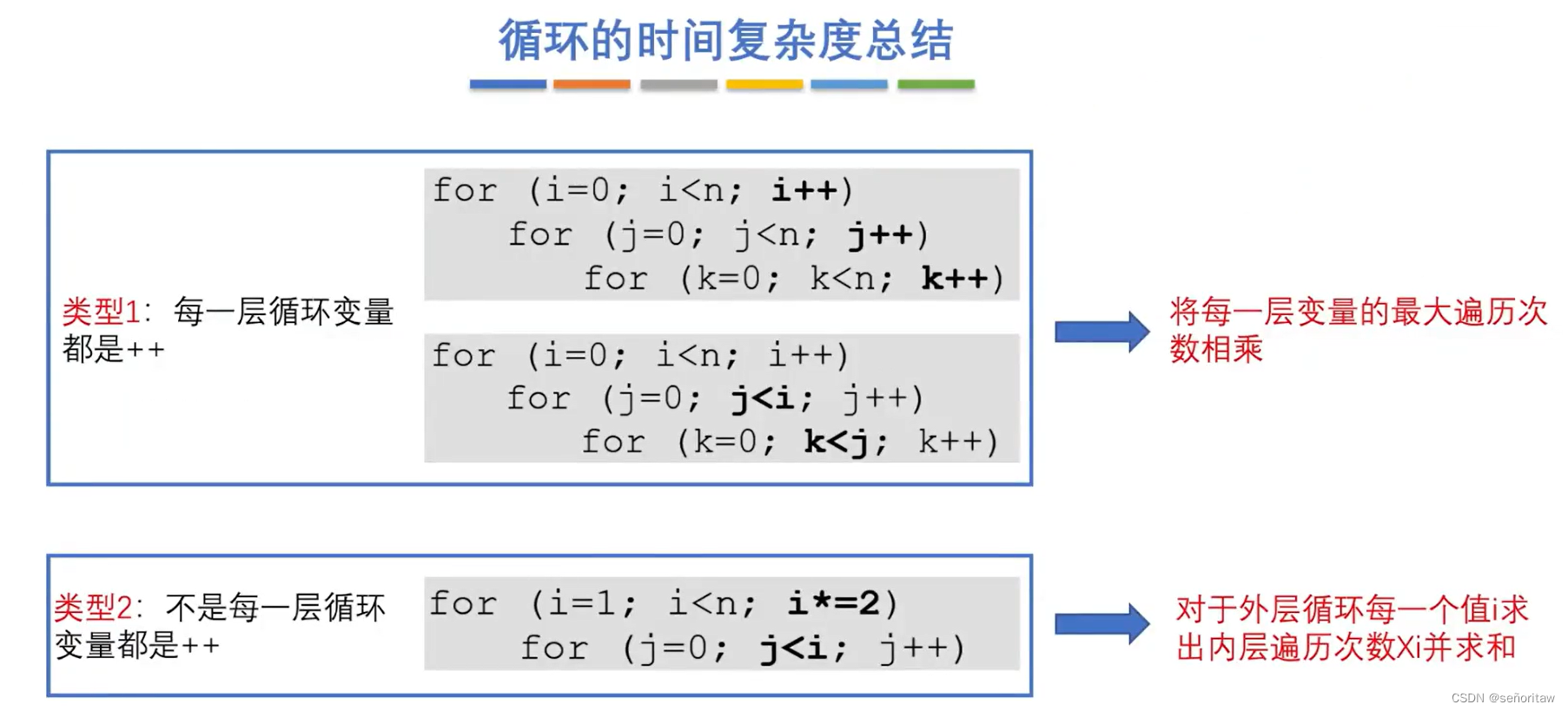
二、综合应用题
01.分析以下各程序段,求出算法的时间复杂度。
① i=1;k=0;
while(i<n-1){
k=k+10*i;i++;
② y=0;
while((y+1)*(y+1)<=n)
y=y+1;
③ for(i=0;i<n;i++)
for(j=0;j<m;j++)
a[i][j]=0;
①基本语句k=k+10*i共执行了n-2次,所以T(n)= O(n)。
②设循环体共执行t次,每循环一次,循环变量y加1,最终t=y。故t²≤n,得T(n)=O(n1/2)。
③内循环执行m次,外循环执行n次,根据乘法原理,共执行了mxn次,故T(m, n)=O(mxn)。
相关文章:

算法简单试题
一、选择题 01.一个算法应该是( B ). A.程序 B.问题求解步骤的描述 C.要满足五个基本特性 D.A和C 02.某算法的时间复杂度为O(n),则表示该…...

CSS 自测题 -- 用 flex 布局绘制骰子(一、二、三【含斜三点】、四、五、六点)
一点 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><title>css flex布局-画骰子</title><sty…...

蓝桥集训之牛的学术圈 I
蓝桥集训之牛的学术圈 I 核心思想:二分 确定指数x后 判断当前c[i]是否>x(满足条件) 并记录次数同时记录 1后满足条件的个数最后取bns和m的最小值 为满足条件的元素个数ansbns为当前指数x下 满足条件的元素个数 #include <iostream>#include <cstring…...

软件设计师软考题目解析21 --每日五题
想说的话:要准备软考了。0.0,其实我是不想考的,但是吧,由于本人已经学完所有知识了,只是被学校的课程给锁在那里了,不然早找工作去了。寻思着反正也无聊,就考个证玩玩。 本人github地址…...

python读写json文件详解
在Python中,可以使用json模块来读写JSON格式的文件。下面是一个详细的示例,演示了如何读写JSON文件: import json# 写入JSON文件 data {"name": "John","age": 30,"city": "New York" }…...

#include<ros/ros.h>头文件报错
快捷键 ctrl shift B 调用编译,选择:catkin_make:build)(要先在vscode上添加扩展:ros) 可以点击配置设置为默认,修改.vscode/tasks.json 文件 修改.vscode/tasks.json 文件,否则ros.h头文件会报错 内容修改为以下内…...
mybatis单表curd笔记(尚硅谷
Mybatis 11111ibatis和mybatis不同 查询文档mybatis的日志输出id赋值输入(向sql语句传入数据单个简单类型单个实体对象多个简单类型map类型 输出数据的指定单个简单类型单个实体类型输出map类型输出list输出类型主键回显(自增长类型主键回显(…...

在线重定义-操作步骤
第一步:验证表是否能被在线重定义 验证是否能按主键重定义(默认,最后一次参数可以不加) 1 2 3 4 begin --dbms_redefinition.can_redef_table(scott,tb_cablecheck_equipment_bak); dbms_redefinition.can_redef_table(scot…...
16:00面试,16:06就出来了,问的问题过于变态了。。。
从小厂出来,没想到在另一家公司又寄了。 到这家公司开始上班,加班是每天必不可少的,看在钱给的比较多的份上,就不太计较了。没想到2月一纸通知,所有人不准加班,加班费不仅没有了,薪资还要降40%…...

基于dashscope在线调用千问大模型
前言 dashscope是阿里云大模型服务平台——灵积提供的在线API组件。基于它,无需本地加载大模型,通过在线方式访问云端大模型来完成对话。 申请API key 老规矩:要想访问各家云端大模型,需要先申请API key。 对于阿里云&#x…...

【Python】可变数据类型 不可变数据类型 || hash
🚩 WRITE IN FRONT 🚩 🔎 介绍:"謓泽"正在路上朝着"攻城狮"方向"前进四" 🔎🏅 荣誉:2021|2022年度博客之星物联网与嵌入式开发TOP5|TOP4、2021|2222年获评…...
MySQL 篇-深入了解多表设计、多表查询
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 多表设计概述 1.1 多表设计 - 一对多 1.2 多表设计 - 一对一 1.3 多表设计 - 多对多 2.0 多表查询概述 2.1 多表查询 - 内连接 2.2 多表查询 - 外连接 2.3 多表查…...

【Java】Spring的ReflectionUtils类常用方法学习笔记
目录 ReflectionUtils介绍 常用方法 访问字段 方法调用 处理回调 示例 脑容量不够了,以简单的小知识作为一天的结尾吧(悲 ReflectionUtils介绍 ReflectionUtils是Spring Framework中非常实用的一个工具类,为开发人员提供了简便的反射操作方法&am…...

内存函数详解
1. memcpy函数 void * memcpy ( void * destination, const void * source, size_t num ); 1.1 函数的功能,使用与注意事项 1. memcpy函数的作用是内存拷贝,即将source指向的空间中的num个字节拷贝到destination指向的空间中去,然后返回de…...
)
事务(transaction)
事务,什么是事务,事务就是由单独单元的一个或多个sql语句组成,在这个单元中,每个sql语句都是相互依赖的。而整个单独单元是作为一个不可分割的整体存在,类似于物理当中的原子(一种不可分割的最小单位&#…...

Linux之cd、pwd、mkdir 命令
cd命令,切换目录 1)当Linux终端(命令行)打开的时候,会默认以用户的HOME目录作为当前的工作目录。 2)我们可以通过cd命令,更改当前所在的工作目录。 3)cd命令来自英文:C…...

【python高级编程教程】笔记(python教程、python进阶)第三节:(1)多态与鸭子类型(Polymorphism and Duck Typing)
参考文章1:【比刷剧还爽】清华大佬耗时128小时讲完的Python高级教程!全套200集!学不会退出IT界! 参考文章2:清华教授大力打造的Python高级核心技术!整整100集,强烈建议学习(Python3…...
)
学习JAVA的第十五天(基础)
目录 数据结构 二叉树 二叉查找树 平衡二叉树 红黑树 Set系列集合 HashSet集合 LinkedHashSet集合 TreeSet集合 前言:学习JAVA的第十四天(基础)-CSDN博客 数据结构 二叉树 元素:结点&am…...
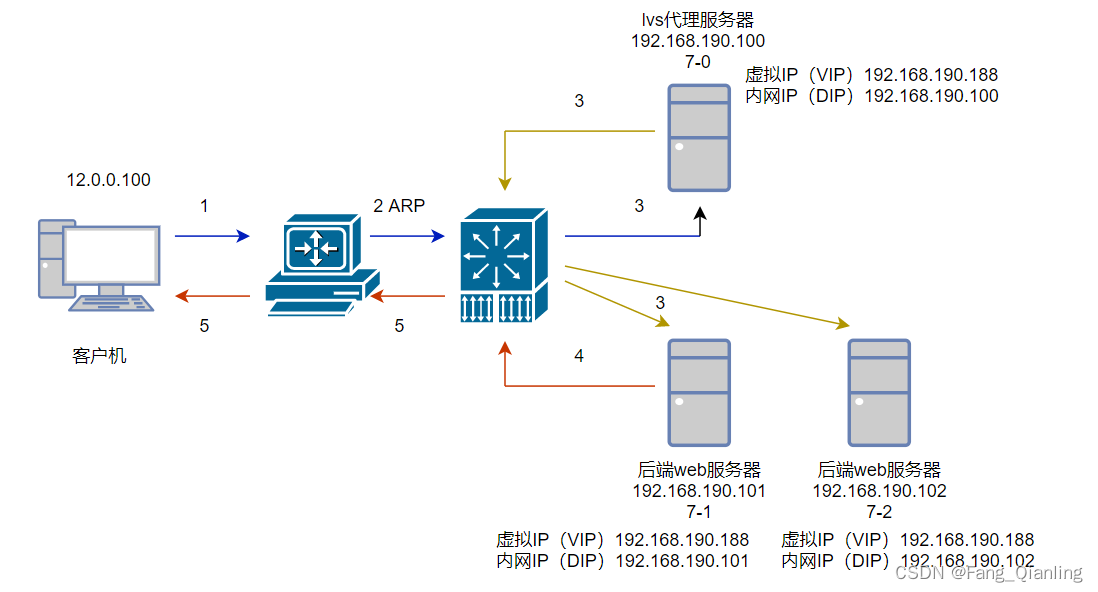
LVS四层负载均衡集群
简介 LVS(Linux Virtual Server)即Linux虚拟服务器,是由章文嵩博士主导的开源负载均衡项目,目前LVS已经被集成到Linux内核模块中。该项目在Linux内核中实现了基于IP的数据请求负载均衡调度方案,终端互联网用户从外部访…...
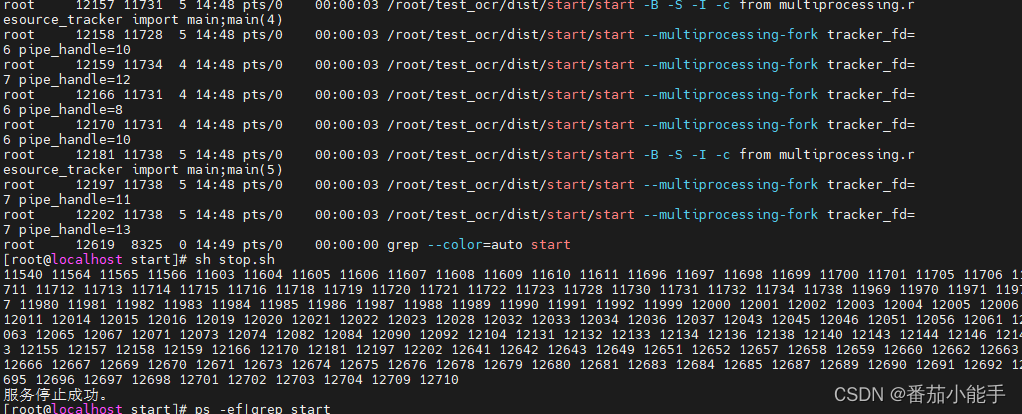
【pyinstaller打包记录】程序使用多进程,打包后,程序陷入死循环
简介 PyInstaller 是一个用于将 Python 程序打包成可执行文件(可执行程序)的工具。它能够将 Python 代码和其相关的依赖项(包括 Python 解释器、依赖的模块、库文件等)打包成一个独立的可执行文件,方便在不同环境中运行…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...
