学习JAVA的第十五天(基础)
目录
数据结构
二叉树
二叉查找树
平衡二叉树
红黑树
Set系列集合
HashSet集合
LinkedHashSet集合
TreeSet集合
前言:学习JAVA的第十四天(基础)-CSDN博客
数据结构
二叉树
元素:结点(节点)
度:每个节点的子节点数量
二叉树:度<=2
树高:树的总层数
根节点:最顶部的节点
左子结点:左下方的节点
右子节点:右下方的节点
二叉查找树
特点:
每个节点最多有2个子节点
任意节点左子树上的值小于当前节点
任意节点右子树上的值大于当前节点
添加节点:
小的存左边、大的存右边、一样的不存
遍历方式:
①前序遍历
②中序遍历
③ 后序遍历
④ 层序遍历
前序遍历
从根节点开始,按照当前节点、左子节点、右子节点的顺序遍历
中序遍历
从最左边的子节点开始,按照左子节点、当前节点、右子节点的顺序遍历
后序遍历
从最左边的子节点开始,按照左子节点、、右子节点、当前节点的顺序遍历
层序遍历
从根节点开始,一层一层遍历
平衡二叉树
规则: 任意节点的左右子树高度差不超过1
旋转机制
当添加一个节点时,该树不是一个平衡二叉树
左旋
确认支点:从添加的节点开始,不断的从父节点中找出不平衡的节点
步骤:不平衡节点作为支点。将支点左旋降级,变成左子节点。晋升原来的右子节点
右旋
确认支点:从添加的节点开始,不断的从父节点中找出不平衡的节点
步骤:不平衡节点作为支点。将支点右旋降级,变成右子节点。晋升原来的左子节点
红黑树
特征:
红黑树是一种自平衡的二叉树
每个节点可以是红或黑,红黑树不是高度平衡的,它的平衡是通过“红黑规则”实现
红黑规则:
①每个节点是红色或者是黑色的
②根节点必须是黑色的
③如果一个节点没有子节点或者父节点,则该节点的指针属性值为Nil,这些Nil会视为叶节点,每个叶节点是黑色的
④如果某一个节点是红色,那么它的子节点必须是黑色(不能出现两个红色节点相连)
⑤对每一个节点,从该节点到其所有后代叶节点的简单路径.上,均包含相同数目的黑色节点
添加节点:
默认是红色(效率高)
Set系列集合
特点:
无序:存取顺序不一致
不重复:可以用来去重
无索引: 不能用索引遍历元素
Set实现类:
- HashSet:无序、不重复、无索引
- LinkedHashSet:有序、不重复、无索引
- TreeSet:可排序、不重复、无索引
Set集合遍历测试类
public static void main(String[] args) {//创建Set集合对象 利用多态Set<String> s = new HashSet<>();//添加元素s.add("aaa");s.add("bbb");s.add("ccc");//打印集合System.out.print(s);//[aaa, ccc, bbb]//创建迭代器对象Iterator<String> it = s.iterator();while (it.hasNext()){System.out.print(it.next());//aaacccbbb}//增强for遍历for(String str : s) {System.out.print(str);//aaacccbbb}System.out.println();//利用Lambda表示式遍历s.forEach(new Consumer<String>() {@Overridepublic void accept(String str) {System.out.print(str);}});//简化Lambda表达式s.forEach(str -> System.out.print(str));//aaacccbbb}HashSet集合
解释:底层是用哈希表存储数据的
哈希表:
JDK8之前:数组+链表
JDK8开始:数组+链表+红黑树
哈希值:对象的整数表现形式
- 根据hashCode方法算出来的int类型整数
- 该方法定义在Object中,所有对象都可以调用,默认使用地址值计算哈希值
- 一般情况下,会重写hashCode方法,利用对象内部的属性值计算哈希值
测试类
public static void main(String[] args) {//创建对象Student s1 = new Student("zhj",32);Student s2 = new Student("zhj",32);//哈希值System.out.println(s1.hashCode());//2133927002System.out.println(s2.hashCode());//1836019240}LinkedHashSet集合
原理:底层数据结构依然是哈希表,只是每个元素又多了双链表的机制记录存储数据的顺序
测试类
public static void main(String[] args) {//创建对象Student s1 = new Student("aaa",12);Student s2 = new Student("bbb",15);Student s3 = new Student("ccc",18);Student s4 = new Student("ddd",42);//创建集合的对象LinkedHashSet<Student> lhs = new LinkedHashSet<>();System.out.println(lhs.add(s3));//trueSystem.out.println(lhs.add(s2));//trueSystem.out.println(lhs.add(s1));//trueSystem.out.println(lhs.add(s4));//trueSystem.out.println(lhs);//[Student{name='ccc', age=18}, Student{name='bbb', age=15}, Student{name='aaa', age=12}, Student{name='ddd', age=42}]}TreeSet集合
特点:可排序(默认情况按照从小到大排列)、无索引、不重复
实现:TreeSet集合底层是基于红黑树的数据结构进行排序的
测试类:
public static void main(String[] args) {//创建TreeSet集合对象TreeSet<Integer> ts = new TreeSet<>();//添加元素ts.add(4);ts.add(8);ts.add(1);ts.add(3);ts.add(2);//打印数据System.out.println(ts);//[1, 2, 3, 4, 8]//迭代器遍历Iterator<Integer> it = ts.iterator();while(it.hasNext()){System.out.print(it.next());//12348}//增强for遍历for (Integer t : ts) {System.out.print(t);//12348}//实现类ts.forEach(new Consumer<Integer>() {@Overridepublic void accept(Integer integer) {System.out.print(integer);//12348}});//Lambda表达式简化ts.forEach(integer -> System.out.print(integer));//12348}
相关文章:
)
学习JAVA的第十五天(基础)
目录 数据结构 二叉树 二叉查找树 平衡二叉树 红黑树 Set系列集合 HashSet集合 LinkedHashSet集合 TreeSet集合 前言:学习JAVA的第十四天(基础)-CSDN博客 数据结构 二叉树 元素:结点&am…...
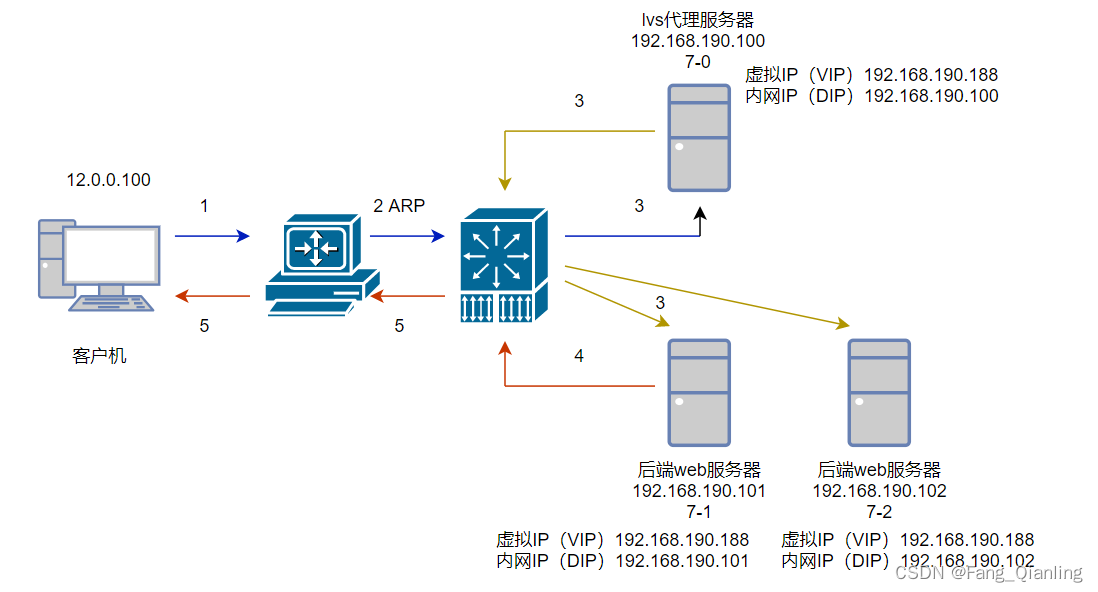
LVS四层负载均衡集群
简介 LVS(Linux Virtual Server)即Linux虚拟服务器,是由章文嵩博士主导的开源负载均衡项目,目前LVS已经被集成到Linux内核模块中。该项目在Linux内核中实现了基于IP的数据请求负载均衡调度方案,终端互联网用户从外部访…...
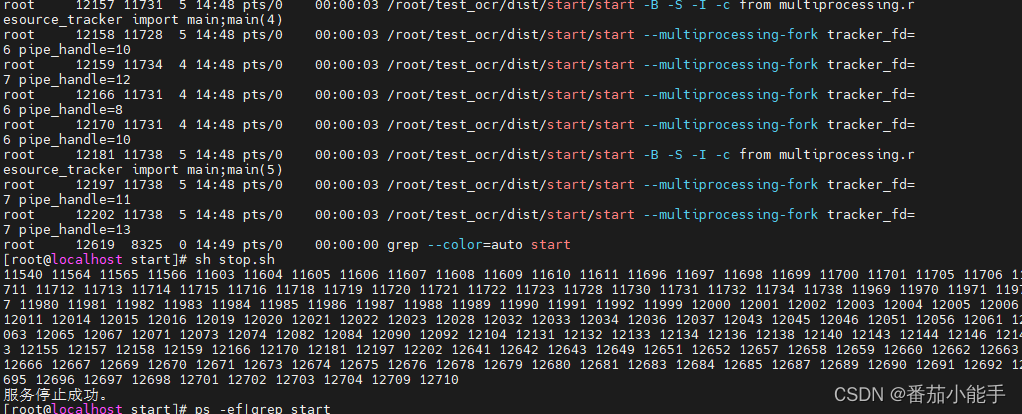
【pyinstaller打包记录】程序使用多进程,打包后,程序陷入死循环
简介 PyInstaller 是一个用于将 Python 程序打包成可执行文件(可执行程序)的工具。它能够将 Python 代码和其相关的依赖项(包括 Python 解释器、依赖的模块、库文件等)打包成一个独立的可执行文件,方便在不同环境中运行…...

MAC | linux | SSH 密钥验证
SSH密钥登陆过程 客户端通过ssh-keygen生成自己的公钥和私钥。手动将客户端的公钥放入远程服务器的指定位置。客户端向服务器发起 SSH 登录的请求。服务器收到用户 SSH 登录的请求,发送一些随机数据给用户,要求用户证明自己的身份。客户端收到服务器发来…...

【AI Agent系列】【MetaGPT多智能体学习】3. 开发一个简单的多智能体系统,兼看MetaGPT多智能体运行机制
本系列文章跟随《MetaGPT多智能体课程》(https://github.com/datawhalechina/hugging-multi-agent),深入理解并实践多智能体系统的开发。 本文为该课程的第四章(多智能体开发)的第一篇笔记。主要记录下多智能体的运行…...
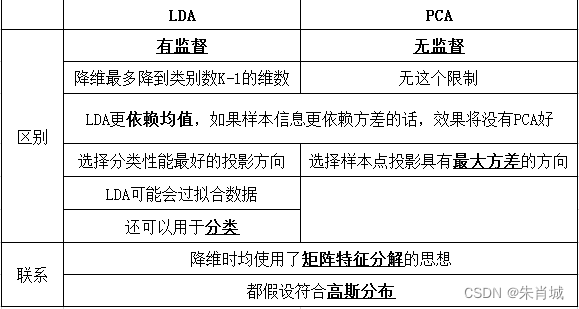
机器学习-面经(part7、无监督学习)
机器学习面经系列的其他部分如下所示: 机器学习-面经(part1) 机器学习-面经(part2)-交叉验证、超参数优化、评价指标等内容 机器学习-面经(part3)-正则化、特征工程面试问题与解答合集机器学习-面经(part4)-决策树共5000字的面试问题与解答…...
teknoparrot命令行启动游戏
官方github cd 到teknoparrot解压目录 cd /d E:\mn\TeknoParrot2_cp1\GameProfiles启动游戏 TeknoParrotUi.exe --profile游戏配置文件游戏配置文件位置/UserProfiles,如果UserProfiles文件夹里没有那就在/GameProfiles,在配置文件里将游戏路径加入之间,或者打开模拟器设置 …...
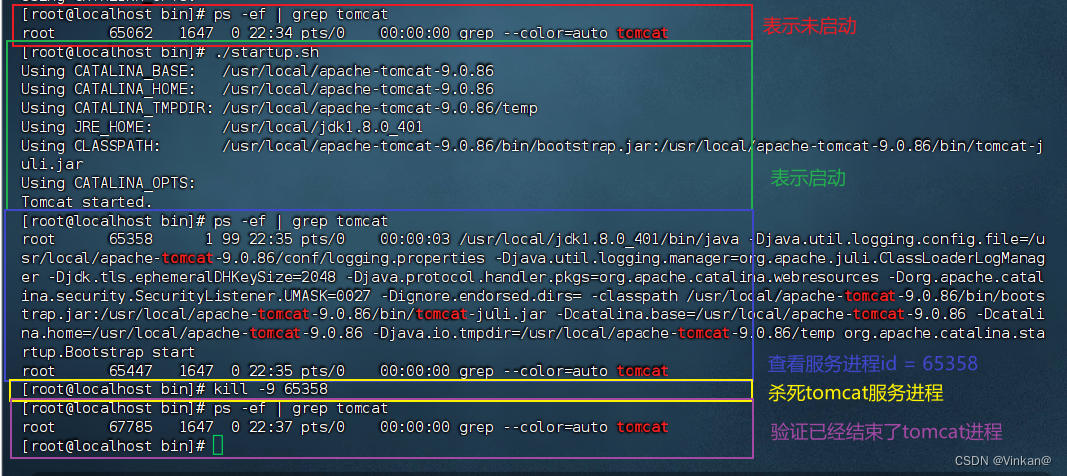
停止Tomcat服务的方式
运行脚本文件停止 运行Tomcat的bin目录中提供的停止服务的脚本文件 关闭命令 # sh方式 sh shutdown.sh# ./方式 ./shutdown.sh操作步骤 运行结束进程停止 查看Tomcat进程,获得进程id kill进程命令 # 执行命令结束进程 kill -9 65358 操作步骤 注意 kill命令是…...
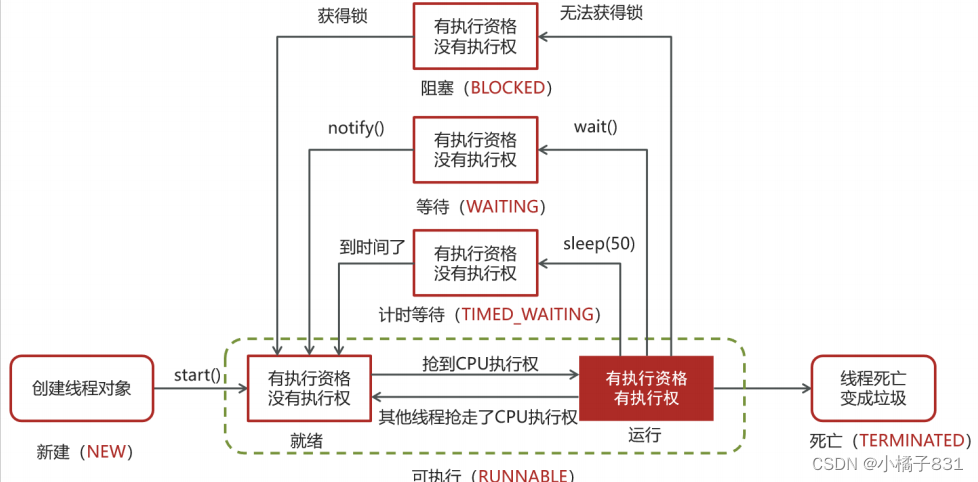
多线程相关面试题(2024大厂高频面试题系列)
1、聊一下并行和并发有什么区别? 并发是同一时间应对多件事情的能力,多个线程轮流使用一个或多个CPU 并行是同一时间动手做多件事情的能力,4核CPU同时执行4个线程 2、说一下线程和进程的区别? 进程是正在运行程序的实例ÿ…...
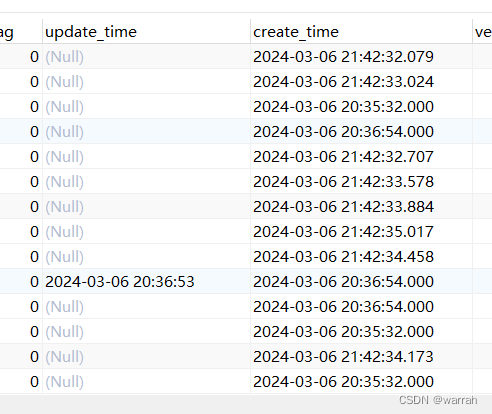
mysql 时间精度问题
timestamp到2038年,还有14年时间,一个系统如果能活到那一刻也是相当不错了。 这里先看一下个datetime的问题,下面的插入数据的时间戳是2024-03-06 21:20:50.839 INSERT INTO psi_io_balance ( id, as_id, bill_date, order_id, busi_type, direction, c…...
)
基于python的爬虫原理和管理系统实现(代码下载)
Python实现爬虫的原理如下: 发送请求:使用Python中的库,如Requests或urllib,向目标网站发送HTTP请求,获取网页的内容。 解析网页:使用Python中的库,如BeautifulSoup或lxml,对获取的…...

IOS 设置UIViewController为背景半透明浮层弹窗,查看富文本图片详情
使用场景:UIViewController1 打开 UIViewController2(背景半透明弹窗) 案例:打开富文本网页<img>图片的url查看图片详情 WKWebView WKNavigationDelegate代理方法设置js代码点击事件 ///注册添加图片标签点击js方法 - …...

网络层介绍
网络层是OSI模型中的第三层,也称为网络协议层。它主要负责在源主机和目标主机之间提供数据通信的路径选择和控制。网络层通过使用源和目标主机的网络地址来实现数据包的路由和转发。 以下是网络层的一些主要功能: 路由选择:网络层使用路由选…...

springboot/ssm酒店客房管理系统Java在线酒店预约预定平台web
springboot/ssm酒店客房管理系统Java在线酒店预约预定平台web 基于springboot(可改ssm)vue项目 开发语言:Java 框架:springboot/可改ssm vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:…...

分布式测试插件 pytest-xdist 使用详解
使用背景: 大型测试套件:当你的测试套件非常庞大,包含了大量的测试用例时,pytest-xdist可以通过并行执行来加速整体的测试过程。它利用多个进程或计算机的计算资源,可以显著减少测试执行的时间。高计算资源需求&#…...
)
【S32K3 MCAL配置】-1.1-GPIO配置及其应用-点亮LED灯(基于MCAL)
目录(共13页精讲,手把手教你S32K3从入门到精通) 实现的架构:基于MCAL层 前期准备工作: 1 创建一个FREERTOS工程...
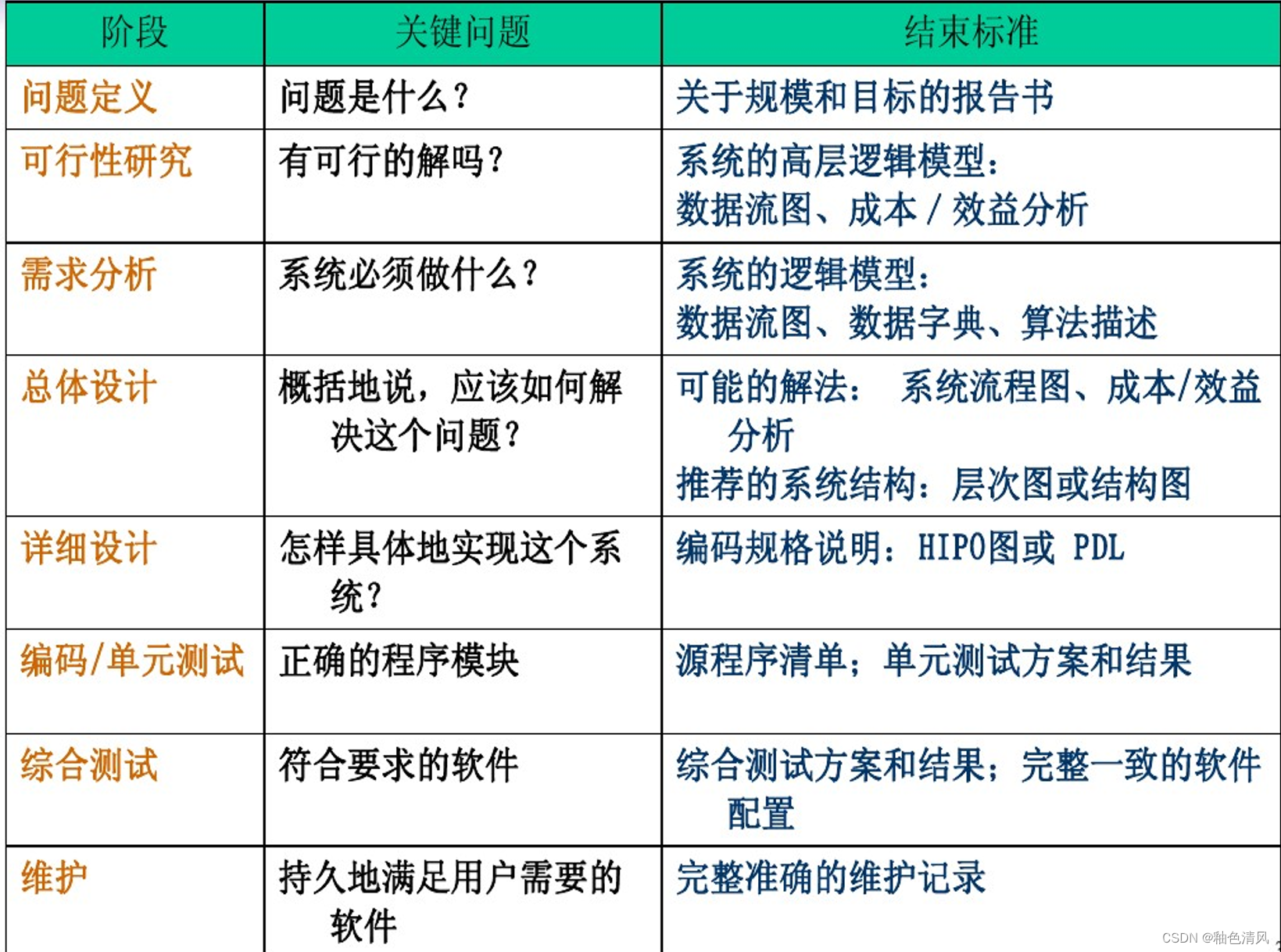
【软件工程】软件工程定义、软件危机以及软件生命周期
🌸博主主页:釉色清风🌸文章专栏:软件工程🌸 今日语录:What matters isn’t how others think of your ambitions but how fervently you cling to them. 软件工程系列,主要根据老师上课所讲提及…...

24计算机考研深大经验分享(计算机专业考研综合安排)
文章目录 背景科目选择高数选课一轮二轮冲刺阶段 线代一轮二轮 概率论计算机学科专业基础408数据结构计算机组成原理操作系统计算机网络总结 英语政治 末言 背景 首先贴一下初试成绩。这篇分享主要是给零基础的同学使用的,基础好的同学可以自行了解补充一下…...

【知识整理】MySQL数据库开发设计规范
一、规范背景与目的 MySQL数据库与 Oracle、 SQL Server 等数据库相比,有其内核上的优势与劣势。我们在使用MySQL数据库的时候需要遵循一定规范,扬长避短。 本规范旨在帮助或指导RD、QA、OP等技术人员做出适合线上业务的数据库设计。在数据库变更和处理…...

Vue自定义组件实现v-model
前言 v-model 实际上就是 $emit(input) 以及 props:value 的组合语法糖。 1.封装自定义组件 要在 Vue 中实现自定义组件的 v-model 功能,你可以通过使用 model 选项来定义组件的 prop 和事件。以下是一个示例代码,演示如何实现一个自定义组件并使用 v…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
