【蓝桥杯集训·每日一题】AcWing 1488. 最短距离
文章目录
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 三、知识风暴
- Dijkstra算法
一、题目
1、原题链接
1488. 最短距离
2、题目描述
有 N 个村庄,编号 1 到 N。
村庄之间有 M 条无向道路,第 i 条道路连接村庄 ai 和村庄 bi ,长度是 ci。
所有村庄都是连通的。
共有 K 个村庄有商店,第 j 个有商店的村庄编号是 xj。
然后给出 Q 个询问,第 k 个询问给出一个村庄的编号 yk,问该村庄距离最近的商店有多远?
输入格式
第一行包含两个整数 N,M。
接下来 M 行,每行包含三个整数 ai,bi,ci,表示第 i 条道路连接村庄 ai 和村庄 bi,长度是 ci。
再一行包含整数 K。
接下来 K 行,每行包含一个整数 xj,表示第 j 个有商店的村庄编号是 xj。
再一行包含整数 Q。
接下来 Q 行,每行包含一个整数 yk,表示询问编号为 yk 的村庄与其距离最近的商店之间的距离。
输出格式
对于每个询问,输出该询问的结果。
数据范围
2≤N≤105,N−1≤M≤min(N(N−1)/2,105),1≤Q≤105,1≤K≤N,1≤ci≤10000
输入样例:
7 7 1 2 5 1 4 3 2 3 2 2 5 1 3 6 7 5 6 8 6 7 6 3 7 5 4 7 1 2 3 4 5 6 7输出样例:
3 1 3 0 0 6 0
二、解题报告
1、思路分析
思路来源:y总讲解视频
y总yyds
(1)将每个商店看做起点,在图中添加一个虚拟源点(起点),该点到其后面所有商店的距离均为0(有向边),则可以将从村庄走到商店的最短路径转化为从村庄走到源点(也就是从源点到村庄)的最短路径,两者等价。
(2)模拟上述过程,求从虚拟源点到村庄的最短路径,即为从村庄到商店的最短路径。
2、时间复杂度
时间复杂度为O(mlogn)(n表示点数,m表示边数)
3、代码详解
#include <iostream>
#include <queue>
#include <cstring>
#include <utility>
using namespace std;
typedef pair<int,int> PII;
const int N=100010,M=3*N; //N代表点数,M代表边数,因需要为每个起点添加一条由虚拟源点指向的边,所以开成点数3倍
int dist[N]; //存储每个点到虚拟源点的最短路径
int h[N],e[M],w[M],ne[M],idx; //h[]存储每个点第一条边的idx,e[]存储每条边的终点,ne[]存储每条边同起点的下一条边的idx,idx存储边的编号
bool st[N];
int n,m;
//邻接表中添加一条边
void add(int a,int b,int c){e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;
}
//堆优化dijkstra求最短路
int dijkstra(){memset(dist,0x3f,sizeof dist);priority_queue<PII,vector<PII>,greater<PII>> heap;dist[0]=0;heap.push({0,0});while(!heap.empty()){PII t=heap.top();heap.pop();int ver=t.second;if(st[ver]) continue;st[ver]=true;for(int i=h[ver];i!=-1;i=ne[i]){int j=e[i];if(dist[j]>dist[ver]+w[i]){dist[j]=dist[ver]+w[i];heap.push({dist[j],j});}}}if(dist[n]==0x3f3f3f3f) return -3;else return dist[n];
}
int main(){cin>>n>>m;memset(h,-1,sizeof h);while(m--){int a,b,c;cin>>a>>b>>c;add(a,b,c);add(b,a,c);}int k;cin>>k;while(k--){int x;cin>>x;add(0,x,0); //添加一个虚拟源点到每个商店距离为0的有向边}dijkstra();int q;cin>>q;while(q--){int y;cin>>y;cout<<dist[y]<<endl;}return 0;
}
三、知识风暴
Dijkstra算法
- 基本思想:将一个带权有向图中的顶点分成两组,一组是未确定最短路的,一组是已确定最短路的。每次将未确定最短路集合中的点,按照与源点的距离递增加入已确定最短路的集合中,同时每次往已确定最短路集合中加入一个点后,需要用这个点来更新其他点距离源点的距离。当所有点的最短路都已确定,算法结束。
相关文章:

【蓝桥杯集训·每日一题】AcWing 1488. 最短距离
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴Dijkstra算法一、题目 1、原题链接 1488. 最短距离 2、题目描述 有 N 个村庄,编号 1 到 N。 村庄之间有 M 条无向道路,第 i 条道路连接村庄 ai 和村…...
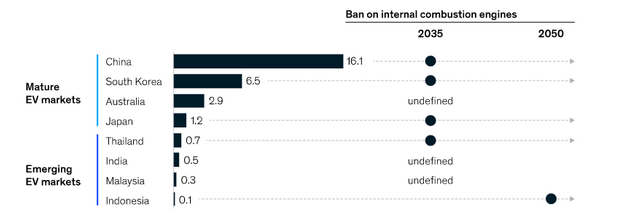
比亚迪:全球最大电动汽车制造商的坎坷成长之路
来源:猛兽财经 作者:猛兽财经 特斯拉(TSLA)首席执行官埃隆马斯克表示,特斯拉最接近的竞争对手可能是一家中国电动汽车公司。猛兽财经认为,沃伦•巴菲特支持的比亚迪(0211)可能是马斯…...

Java开发 - Quartz初体验
前言 在上一篇博客中,我们对单点登录有了初步了解,这也让我们独立做系统有了最基础的保障。但在业务开发中,总是会出现一些定期处理的任务,我们首先想到的是Timer,但由于其调度功能单一,我们实际并不会用它…...
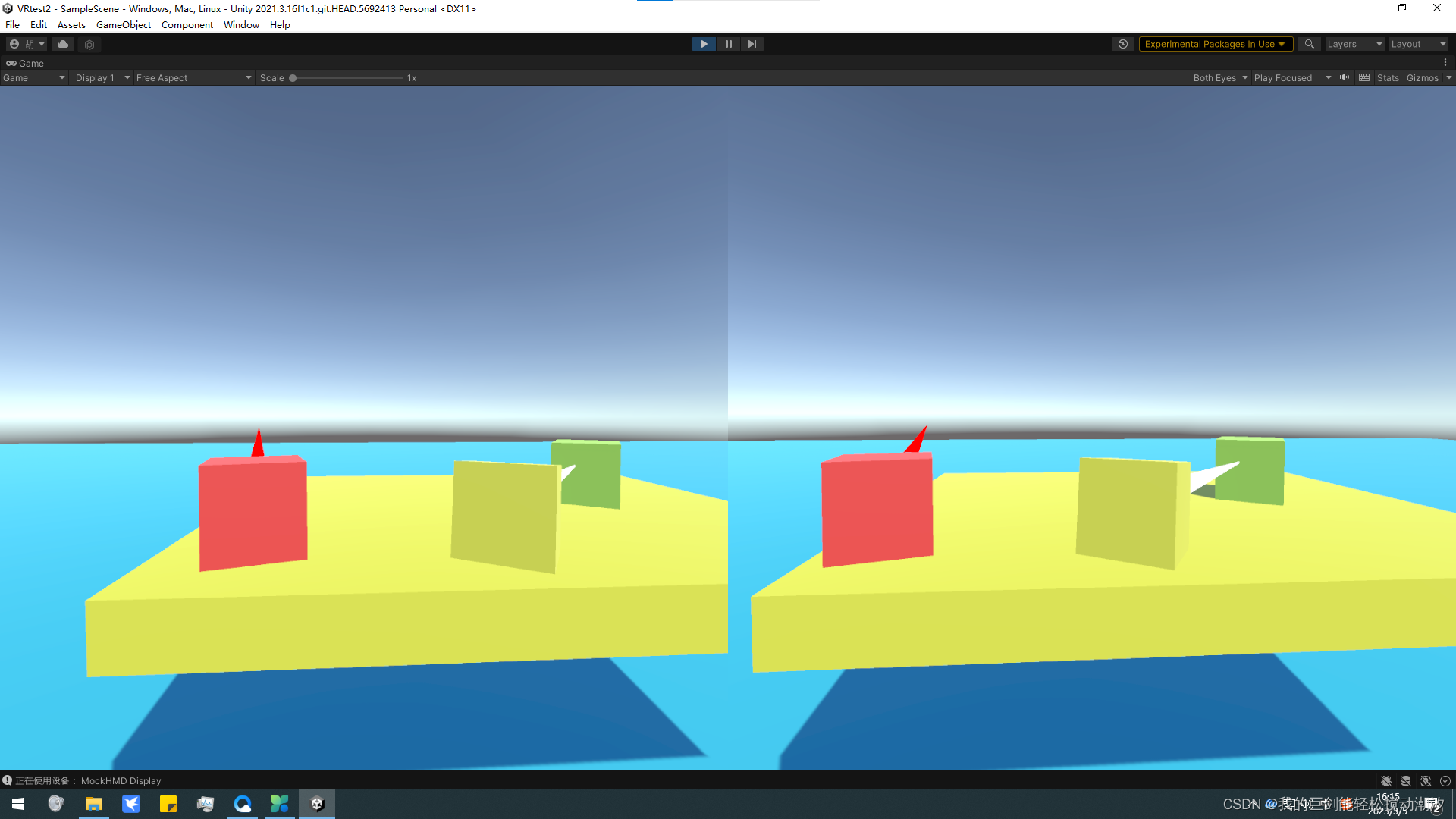
无头盔开发vr XR Device Simulator操作(更新)
1.摄像机(未开启TY键) 平移 上下左右:右键鼠标,移哪去哪 前后:右键快速滚动鼠标滚轮 旋转 XOY平面旋转:右键按住鼠标滚轮滚动鼠标滚轮 XOZ\YOZ平面旋转:右键按住鼠标滚轮移动鼠标 2.左手右手&am…...
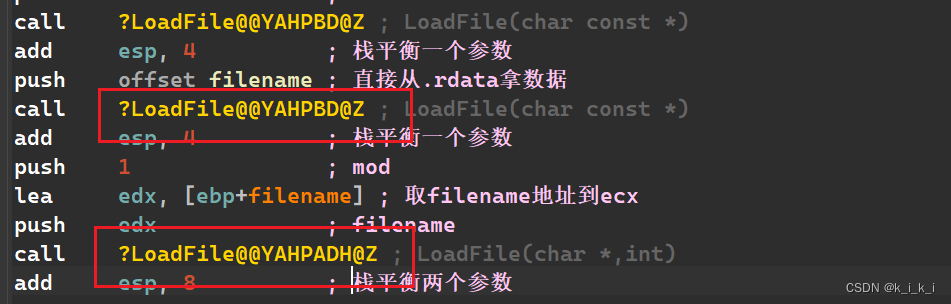
《C++代码分析》第二回:函数重载const char* ,char*,const char[],char[]汇编代码上的区别
一、前言 C相比C是支持函数重载的,现在我们详细探讨一下C函数重载与类方法承载。 二、案例代码 我们编译如下代码,同样的我们关闭代码优化,删除符号链接文(.pdb) #include "windows.h" #include "w…...
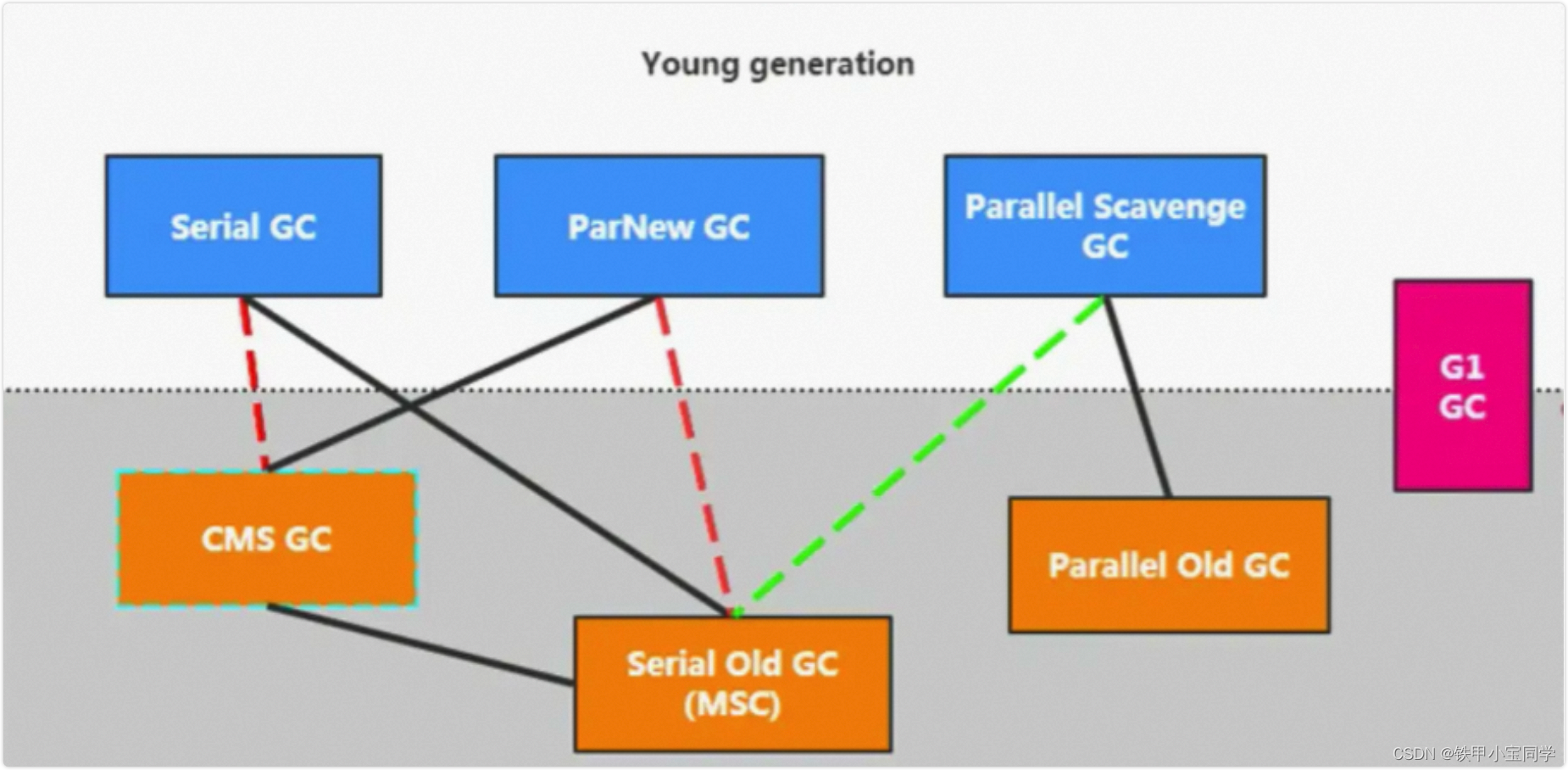
【学习笔记】深入理解JVM之垃圾回收机制
【学习笔记】深入理解JVM之垃圾回收机制 更多文章首发地址:地址 参考: 《深入理解JAVA虚拟机》第三版 第三章尚硅谷 第134 - 203 集参考文章:https://blog.csdn.net/qq_48435252/article/details/123697193 1、概念 🌻 首先我们…...

49.在ROS中实现local planner(2)- 实现Purepersuit(纯跟踪)算法
48.在ROS中实现local planner(1)- 实现一个可以用的模板实现了一个模板,接下来我们将实现一个简单的纯跟踪控制,也就是沿着固定的路径运动,全局规划已经规划出路径点,基于该路径输出相应的控制速度 1. Pur…...
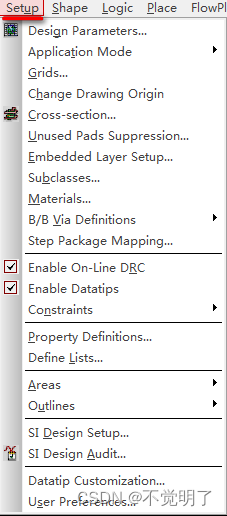
Allegro如何设通孔Pin和Via的消盘操作指导
Allegro如何设通孔Pin和Via的消盘操作指导 用Allegro做PCB设计的时候,除了可以在光绘设置里面设置内层通孔Pin和Via的消盘,在设计过程中,同样也可以设置消盘效果,以便实时显示,如下图 如何设置,具体操作如下 点击Setup点击Unused Pads Suppression...
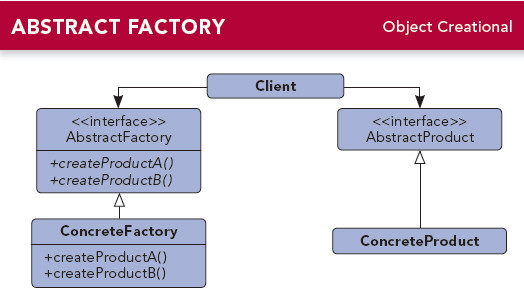
Android工厂模式
工厂模式分为三种 :简单工厂模式 、工厂方法模式 、抽象工厂模式 。 目录 简单工厂模式 UML图 实现 使用场景: 优点 : 缺点: 工厂方法模式 UML图 实现 使用场景: 优点: 缺点: 抽象工厂模式 UM…...

神经网络硬件加速器-架构篇
架构设计 常规架构通常包括两种: 1、全流水线架构,顾名思义,将整个神经网络进行平铺,并对每一层进行优化设计,优点:实现高吞吐率和低延时。缺点:消耗大量硬件资源,通常无法跨网络或…...
)
Python raise用法(超级详细,看了无师自通)
是否可以在程序的指定位置手动抛出一个异常?答案是肯定的,Python 允许我们在程序中手动设置异常,使用 raise 语句即可。 大家可能会感到疑惑,即我们从来都是想方设法地让程序正常运行,为什么还要手动设置异常呢&#…...
1.SpringSecurity快速入门
*SpringScurity的核心功能: 认证:验证当前访问系统的是不是本系统的用户,并且要确认具体是哪个用户 授权:经过认证后判断当前用户是否有权限进行某个操作 *第一步:创建springboot工程 *第二步:引入SpringSecurity依赖 *第三步:写controller,访问对应的url:localhos…...
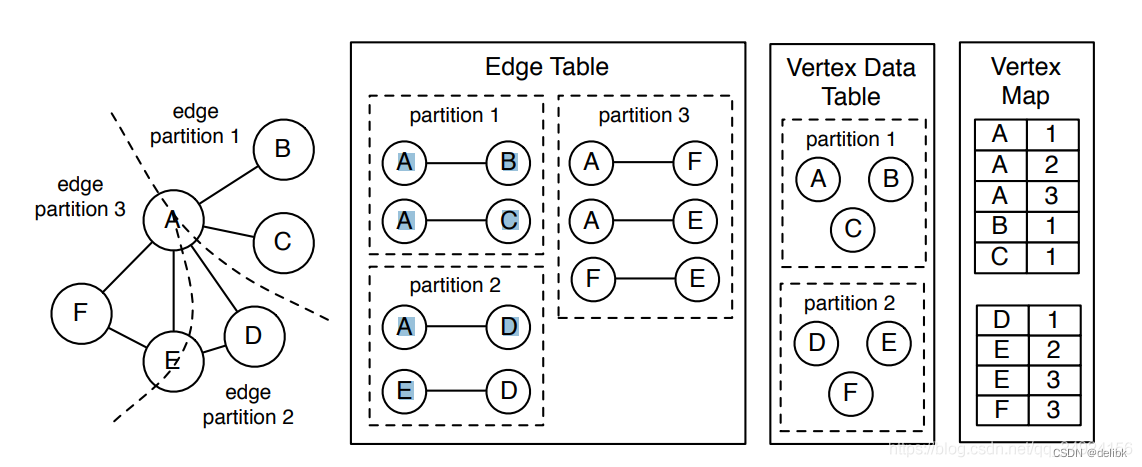
Graph Partition: Edge cut and Vertex cut
Graph PartitionEdge cut and Vertex cutEdge cutVertex cut实际如何进行点分割和边分割的呢?Graph store format情况1:按照边列表存储:情况2:按照邻接表存储:Edge cut and Vertex cut 图结构描述了数据流动ÿ…...

Javascript周学习小结(初识,变量,数据类型)
JS的三大书写方式行内式如图所示:几点说明:JS的行内式写在HTML的标签内部,(常以on开头),如onclick行内式常常使用单引号括住字符串以区分HTML的双引号可读性差,不建议使用引号易出错,不建议使用特殊情况下使…...
C语言-基础了解-10-C函数
C函数 一、C函数 函数是一组一起执行一个任务的语句。每个 C 程序都至少有一个函数,即主函数 main() ,所有简单的程序都可以定义其他额外的函数。 您可以把代码划分到不同的函数中。如何划分代码到不同的函数中是由您来决定的,但在逻辑上&…...
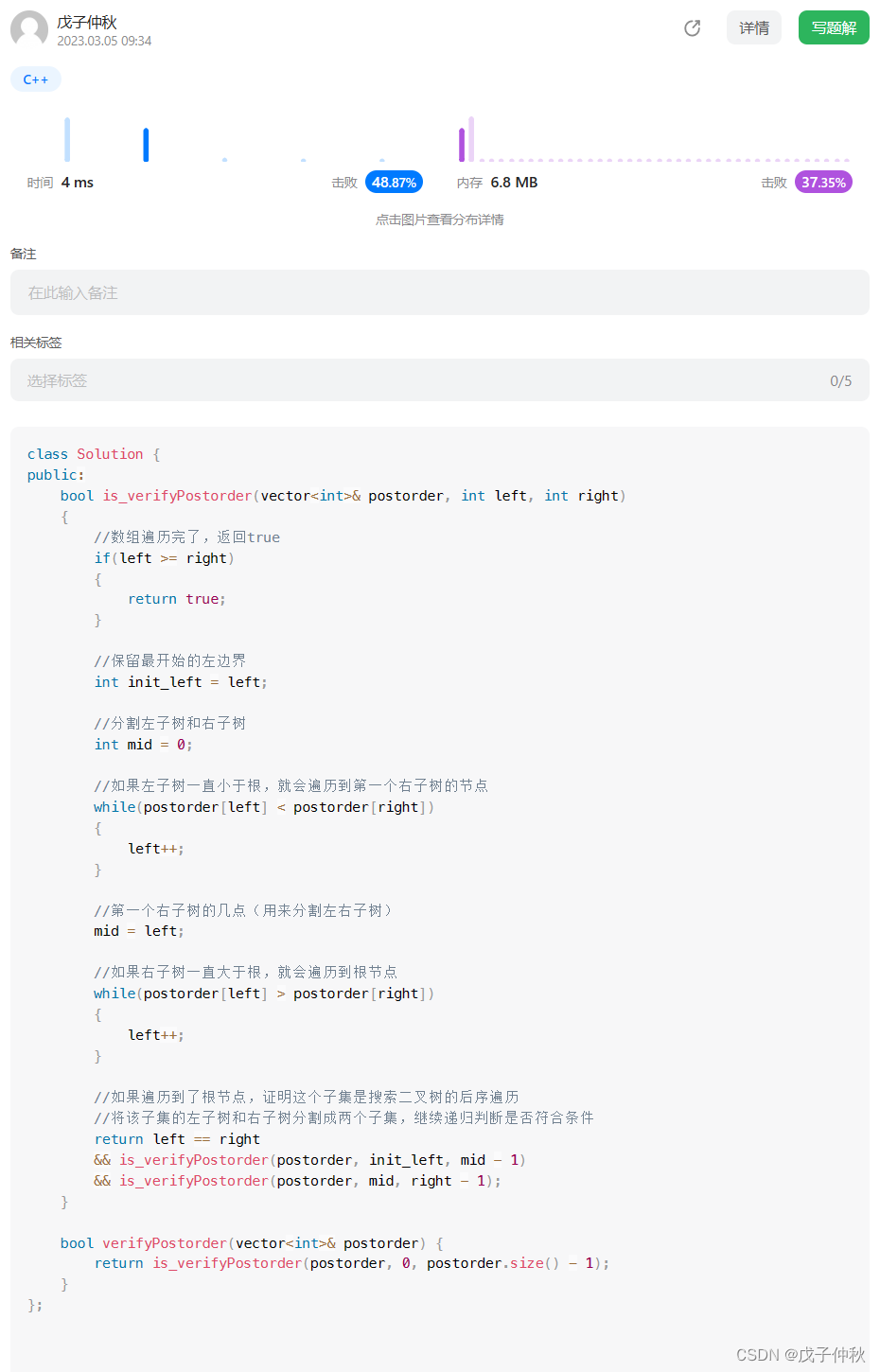
【LeetCode】剑指 Offer(16)
目录 题目:剑指 Offer 33. 二叉搜索树的后序遍历序列 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 写在最后: 题目:剑指 Offer …...
)
第三十九章 linux-并发解决方法二(互斥锁mutex)
第三十九章 linux-并发解决方法二(互斥锁mutex) 文章目录第三十九章 linux-并发解决方法二(互斥锁mutex)互斥锁的定义与初始化互斥锁的DOWN操作互斥锁的UP操作用count1的信号量实现的互斥方法还不是Linux下经典的用法,…...

脚本方式本地仓库jar包批量导入maven私服
脚本内容,将以下内容保存为mavenimport.sh,放置于需要上传的目录下,可以是顶层目录,或者某个分包的目录,若私服已有待上传的包,则执行会被替换 #!/bin/bash # copy and run this script to the root of th…...

【c++】引用的学习
引用的定义和声明 引用是一种别名,它允许使用与原变量相同的内存位置。在C中,引用是使用&符号来定义的。引用必须在定义时初始化,并且可以与原变量分别使用。 int a 10; int& b a; // 定义了一个引用b,它指向a引用的作用…...

linux 软件安装及卸载
1.联网在线安装及卸载ubuntu环境下:使用apt-get 工具apt-get install - 安装软件包apt-get remove - 移除(卸载)软件包CentOS环境下:使用yum工具 (银河麒麟系统属于centos)yum install - 安装软件包yum rem…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...
