C++从零开始的打怪升级之路(day44)
这是关于一个普通双非本科大一学生的C++的学习记录贴
在此前,我学了一点点C语言还有简单的数据结构,如果有小伙伴想和我一起学习的,可以私信我交流分享学习资料
那么开启正题
今天分享的是关于二叉搜索树的知识点
1.二叉搜索树概念
二叉搜索树又叫做二叉排序树,有以下性质(或为空树)
1.左子树结点所有结点的值都小于根节点的值
2.右子树结点所有结点的值都大于根节点的值
3.它的左右子树也都是二叉搜索树
2.二叉搜索树操作
1.查找
a.从根开始比较,查找,如果比跟大往右走,比跟小则往左走
b.最多查找高度次,走到为空还没找到,则这个值不存在
2.插入
a.树为空,直接新增结点,赋值给给_root
b.树不为空,类似查找根据性质找到插入位置,插入新结点
3.删除
首先查找元素是否在二叉搜索树中,如果不存在返回false,存在分为以下几种情况
a.要删除的结点没有左结点
b.要删除的结点没有右结点
c.要删除的结点有左右孩子结点
d.要删除的结点无孩子结点
其中d可以按照a或者b办法解决
情况a:删除该结点且使删除结点的父亲结点指向删除结点的孩子结点——直接删除
情况b:类似于a
情况c:在右子树中找到最小结点(或者在左子树中找到最大节点),用他的值填补到被删除的结点上,再删除此结点——替换法删除
3.二叉搜索树模拟实现
下面给出了模拟实现代码以及测试代码
namespace wkl
{template<class K>struct BSTreeNode{BSTreeNode* _left;BSTreeNode* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};template<class K>class BSTree{typedef BSTreeNode<K> Node;public:bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else{return false;}}//找到空位,开始插入cur = new Node(key);if (key > parent->_key)parent->_right = cur;elseparent->_left = cur;return true;}void _InOrder(Node* root){if (!root)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}void InOrder(){_InOrder(_root);cout << endl;}bool Find(const K& key){Node* cur = _root;while (cur){if (key > cur->_key)cur = cur->_right;else if (key < cur->_key)cur = cur->_left;elsereturn true;}return false;}bool Erase(const K& key){Node* cur = _root;Node* parent = nullptr;while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else{//开始删除//1.左为空//2.右为空//3.左右均不为空if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;}else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;}else{Node* rightMinParent = cur;Node* rightMin = cur->_right; //右子树最小值(最左)while (rightMin->_left){rightMinParent = rightMin;rightMin = rightMin->_left;}cur->_key = rightMin->_key;//改为删除rightMinif (rightMinParent->_left == rightMin)rightMinParent->_left = rightMin->_right;elserightMinParent->_right = rightMin->_right;delete rightMin;}return true;}}return false;}private:Node* _root = nullptr;};void BSTree_Test1(){BSTree<int> BST;int a[] = { 5,3,4,1,7,8,2,6,0,9 };for (auto e : a){BST.Insert(e);}BST.InOrder();int i = 0;for (i = 0; i < 20; i += 2){cout << i << "::";if (BST.Find(i))cout << "Yes";elsecout << "No";cout << endl;}}void BSTree_Test2(){BSTree<int> BST;int a[] = { 5,3,4,1,7,8,2,6,0,9 };for (auto e : a){BST.Insert(e);}BST.InOrder();/*BST.Erase(7);BST.InOrder();*/for (auto e : a){BST.Erase(e);BST.InOrder();}}
}4.二叉搜索树的应用
1.K值模型
K值模型只有key作为关键码,结构中只存储key,关键码即为需要搜索到的值
2.KV模型
每一个关键码都有与之对应的多个Value,即<Key,Value>的键值对
5.二叉搜索树的性能分析
插入和删除都必须先查找,查找效率代表了二叉搜索树的各个操作的性能
最好情况下:二叉树平衡,查找时间复杂度为O(lgN)
最坏情况下:二叉树插入数据接近有序,树长而不平衡,查找时间复杂度为O(N)
新手写博客,有不对的位置希望大佬们能够指出,也谢谢大家能看到这里,让我们一起学习进步吧!
相关文章:
)
C++从零开始的打怪升级之路(day44)
这是关于一个普通双非本科大一学生的C的学习记录贴 在此前,我学了一点点C语言还有简单的数据结构,如果有小伙伴想和我一起学习的,可以私信我交流分享学习资料 那么开启正题 今天分享的是关于二叉搜索树的知识点 1.二叉搜索树概念 二叉搜…...
:类和对象——运算符重载*)
[C++核心编程](七):类和对象——运算符重载*
目录 四则运算符重载 左移运算符重载 递增运算符重载 赋值运算符重载 关系运算符重载 函数调用运算符重载 对已有的运算符重新进行定义,赋予其另一种功能,以适应不同的数据类型 四则运算符重载 对自定义数据类型实现四则运算(加减乘除&…...

什么是MVC和MVVM
**MVC和MVVM是两种流行的软件架构模式,它们在前端开发中被广泛采用来组织代码和管理应用程序的复杂性**。具体如下: MVC(Model-View-Controller): 1. 模型(Model):负责管理数据和业…...

物体检测-系列教程23:YOLOV5 源码解析13 (SPP层、Flatten模块、Concat模块、Classify模块)
😎😎😎物体检测-系列教程 总目录 有任何问题欢迎在下面留言 本篇文章的代码运行界面均在Pycharm中进行 本篇文章配套的代码资源已经上传 点我下载源码 17、SPP模块 17.1 SPP类 SPP是一种特殊的池化策略,最初在YOLOv3-SPP中被使用…...

2024.3.6每日一题
LeetCode 找出数组中的 K -or 值 题目链接:2917. 找出数组中的 K-or 值 - 力扣(LeetCode) 题目描述 给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。 nums 中的 K-or 是一个满足以下条件的非负整数: 只有在 nums 中&…...
YOLOSHOW - YOLOv5 / YOLOv7 / YOLOv8 / YOLOv9 基于 Pyside6 的图形化界面
YOLOSHOW 是一个基于 PySide6(Qt for Python)开发的图形化界面应用程序,主要用于集成和可视化YOLO系列(包括但不限于YOLOv5、YOLOv7、YOLOv8、YOLOv9)的目标检测模型。YOLOSHOW 提供了一个用户友好的交互界面ÿ…...

sql高级
sql高级 SQL SELECT TOP 子句 SELECT TOP 子句用于规定要返回的记录的数目。 SELECT TOP 子句对于拥有数千条记录的大型表来说,是非常有用的。 **注意:**并非所有的数据库系统都支持 SELECT TOP 语句。 MySQL 支持 LIMIT 语句来选取指定的条数数据, O…...

更快更强,Claude 3全面超越GPT4,能归纳15万单词
ChatGPT4和Gemini Ultra被Claude 3 AI模型超越了? 3月4日周一,人工智能公司Anthropic推出了Claude 3系列AI模型和新型聊天机器人,其中包括Opus、Sonnet和Haiku三种模型,该公司声称,这是迄今为止它们开发的最快速、最强…...

devc++小游戏3.8.5
导航: Dev-c跑酷小游戏 1.0.0 devc跑酷小游戏1.2.5 devc跑酷游戏1.2.6 devc跑酷游戏2.0.0 devc跑酷游戏2.0.1 devc跑酷游戏2.4.0 devc跑酷小游戏3.5.0 更新内容 重磅回归,存档搞定!!! 每一关需要前一关已…...
Java网络通信TCP
目录 TCP两个核心类 服务端 1.用ServerSocker类创建对象并且手动指定端口号 2.accept阻塞连接服务端与客户端 3.给客户端提供处理业务方法 4.处理业务 整体代码 客户端 1.创建Socket对象,并连接服务端的ip与端口号 2.获取Socket流对象,写入数据…...

层级锁笔记
注意看test_hierarchy_lock函数:如果thread t2的不注释,就会报错。 这是因为层级锁 更强调单个线程内上锁的顺序。 线程t2已经获取了hmtx2,再试图获取hmtx1就会因为违反层级顺序而抛出异常。 #include <mutex> #include <thread&g…...
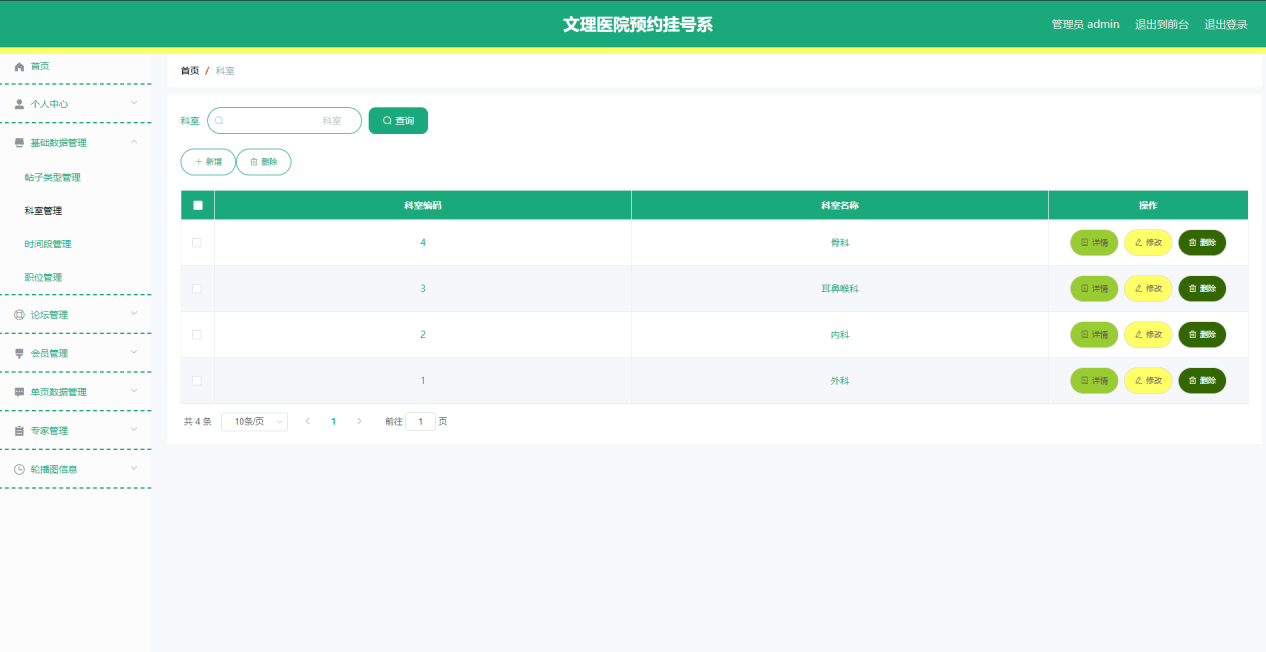
基于SpringBoot+Vue 的专家医院预约挂号系统
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...

计算机基础专升本笔记十二-Excel常用快捷键大全
计算机基础专升本笔记十二-Excel常用快捷键大全 Excel常用快捷键 按键作用Ctrl 0隐藏列Ctrl 1设置单元格格式Ctrl 2添加或取消字体加粗Ctrl 3添加或取消字体倾斜Ctrl 4添加或取消下划线Ctrl 5添加或取消删除线Ctrl 6隐藏或显示图形Ctrl 7隐藏工具栏Ctrl 8隐藏或显示…...

制作耳机壳的UV树脂和塑料材质相比优势有哪些?
制作耳机壳的UV树脂相比塑料材质有以下优势: 高强度与耐磨性:UV树脂具有高强度和耐磨性,能够更好地保护耳机内部零件,延长耳机使用寿命。相比之下,塑料材质可能较易磨损或刮伤。耐高温:UV树脂具有较好的耐…...

JS(JavaScript)中如何实现,复选框checkbox多选功能
起始界面: 代码元素: <p><input type"checkbox" id"checkedAll"> 全选按钮</p><p><input type"checkbox" class"cl"> 选项1</p><p><input type"checkbox&qu…...

直接修改zynq petalinux编译出来的rootfs.cpio.gz文件内容
xilinx zynq petalinux 默认编译打包出的SPI flash烧写启动文件是BOOT.BIN,然而每次需要修改rootfs内的文件时都要重新build rootfs 然后再 package一次才能生成新的BOOT.bin文件,地球人都知道petalinux编译一次是很耗时间的,那么有没有什么简…...

什么是 Golang 类型断言
类型断言:用于检查某个接口是否包含某个具体类型,语法x.(T),x是一个接口类型表达式,T是具体的类型,如果x包含的值可以被转换成T类型,则是ok 在Go语言中,任何类型的值都属于空接口类型。空接口类…...

mysql数据库root权限读写文件
如果没有shell,只有数据库权限的情况下: 1. udf 提权提示没有目录:使用数据流创建目录 1. select xxx into outfile C:\\phpstudy_pro\\Extensions\\MySQL5.5.29\\lib\::$INDEX_ALLOCATION;2. select xxx into outfile C:\\phpstudy_pro\…...

力扣爆刷第88天之hot100五连刷26-30
力扣爆刷第88天之hot100五连刷26-30 文章目录 力扣爆刷第88天之hot100五连刷26-30一、142. 环形链表 II二、21. 合并两个有序链表三、2. 两数相加四、19. 删除链表的倒数第 N 个结点五、24. 两两交换链表中的节点 一、142. 环形链表 II 题目链接:https://leetcode.…...
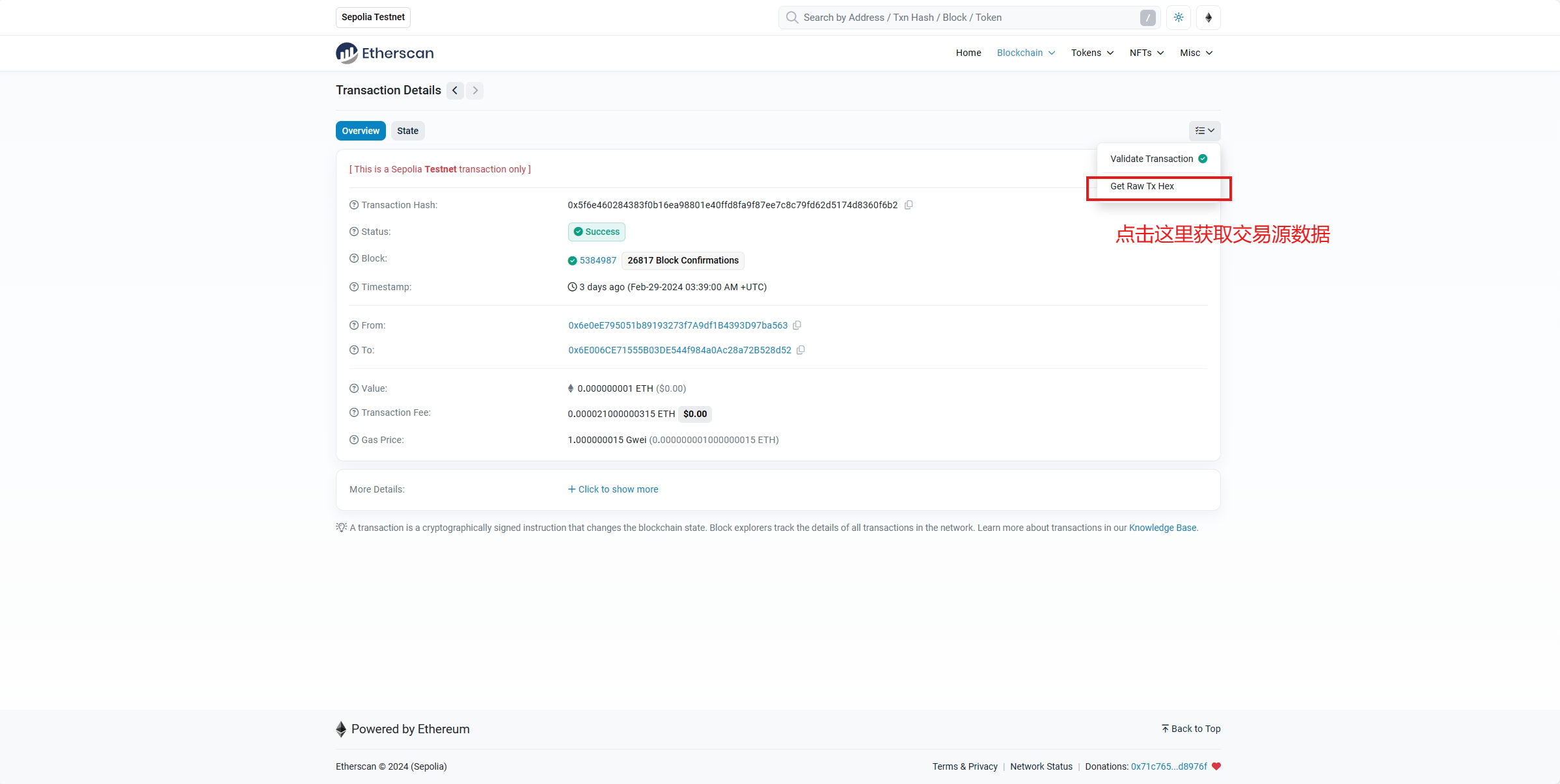
Ethersacn的交易数据是什么样的(2)
分析 Raw Transanction RLP(Recursive Length Prefix)是一种以太坊中用于序列化数据的编码方式。它被用于将各种数据结构转换为二进制格式,以便在以太坊中传输和存储。RLP 是一种递归的编码方式,允许对复杂的数据结构进行编码。所…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
