算法训练day38动态规划基础Leetcode509斐波纳切数70爬楼梯746使用最小花费爬楼梯
什么是动态规划
对于动态规划问题,我将拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组(打印dp数组)
找问题的最好方式就是把dp数组打印出来,看看究竟是不是按照自己思路推导的!
做动规的题目,写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍,心中有数,确定最后推出的是想要的结果。
509 斐波那契数
题目描述
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
题目分析
就像二叉树三部曲
-
确定递归函数的参数和返回值: 确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
-
确定终止条件: 写完了递归算法, 运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出。
-
确定单层递归的逻辑: 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
是有方法论的
这里动规五步曲也是一样
acm模式代码
#include <iostream>
#include <vector>class Solution {
public:int fib(int n) {std::vector<int> dp(n + 1);if (n <= 0) {return 0;}else if (n == 1) {return 1;}dp[0] = 0;dp[1] = 1;for (int i = 2 ; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
};int main() {Solution sol;int n = 5;int sum = sol.fib(n);std::cout << n << "sum:" << sum << std::endl;return 0;
}70. 爬楼梯
题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
示例 2:
输入:n = 3 输出:3 解释:有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶
提示:
1 <= n <= 45
题目分析
爬到第一层楼梯有一种方法,爬到二层楼梯有两种方法。
那么第一层楼梯再跨两步就到第三层 ,第二层楼梯再跨一步就到第三层。
所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来,那么就可以想到动态规划了。
acm模式代码
#include <iostream>
#include <vector>class Solution {
public:int climbStairs(int n) {if (n <= 1) return n;std::vector<int> dp(n + 1);dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
};int main() {Solution sol;int n = 5;int sum = sol.climbStairs(n);std::cout << n << "sum:" << sum << std::endl;return 0;
}746使用最小花费爬楼梯
题目描述
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20] 输出:15 解释:你将从下标为 1 的台阶开始。 - 支付 15 ,向上爬两个台阶,到达楼梯顶部。 总花费为 15 。
示例 2:
输入:cost = [1,100,1,1,1,100,1,1,100,1] 输出:6 解释:你将从下标为 0 的台阶开始。 - 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。 - 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。 - 支付 1 ,向上爬一个台阶,到达楼梯顶部。 总花费为 6 。
提示:
2 <= cost.length <= 10000 <= cost[i] <= 999
题目分析
- 确定dp数组以及下标的含义
使用动态规划,就要有一个数组来记录状态,本题只需要一个一维数组dp[i]就可以了。
dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。
对于dp数组的定义,大家一定要清晰!
- 确定递推公式
可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。
dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?
一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
- dp数组如何初始化
看一下递归公式,dp[i]由dp[i - 1],dp[i - 2]推出,既然初始化所有的dp[i]是不可能的,那么只初始化dp[0]和dp[1]就够了,其他的最终都是dp[0]dp[1]推出。
那么 dp[0] 应该是多少呢? 根据dp数组的定义,到达第0台阶所花费的最小体力为dp[0],那么有同学可能想,那dp[0] 应该是 cost[0],例如 cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 的话,dp[0] 就是 cost[0] 应该是1。
这里就要说明本题力扣为什么改题意,而且修改题意之后 就清晰很多的原因了。
新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 到达 第 0 个台阶是不花费的,但从 第0 个台阶 往上跳的话,需要花费 cost[0]。
所以初始化 dp[0] = 0,dp[1] = 0;
- 确定遍历顺序
最后一步,递归公式有了,初始化有了,如何遍历呢?
本题的遍历顺序其实比较简单,简单到很多同学都忽略了思考这一步直接就把代码写出来了。
acm模式代码
#include <iostream>
#include <vector>
#include <algorithm>class Solution {
public:int minCostClimbingStairs(std::vector<int>& cost) {std::vector<int> dp(cost.size() + 1);// dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。dp[0] = 0;dp[1] = 0;int sum = 0;for (int i = 2; i <= cost.size(); i++) {dp[i] = std::min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);}// for (int i : dp) {// std::cout << i << " ";// }// std::cout << std::endl;// return dp.back();return dp[cost.size()];}
};int main() {std::vector<int> count = {1, 100, 1, 1, 1, 100, 1, 1, 100, 1};Solution sol;int min = sol.minCostClimbingStairs(count);std::cout << "sum: " << min << std::endl;
}相关文章:

算法训练day38动态规划基础Leetcode509斐波纳切数70爬楼梯746使用最小花费爬楼梯
什么是动态规划 对于动态规划问题,我将拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了! 确定dp数组(dp table)以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数组&a…...
Leetcode 206. 反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 示例 1: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1] 示例 2: 输入:head [1,2] 输出:[2,1] 示例 3: 输…...

电子科技大学课程《计算机网络系统》(持续更新)
前言 本校的课程课时有所缩减,因此可能出现与你学习的课程有所减少的情况,因此对其他学校的同学更多的作为参考作用。本文章适合学生的期中期末考试,以及想要考研电子科技大学的同学,电子科技大学同学请先看附言。 第一章 计算…...

HBase介绍、特点、应用场景、生态圈
目录: 一、HBase简介 二、NoSQL和关系型数据库对比 三、HBase特点 四、应用场景 五、HBase生态圈技术 一、HBase简介 HBase是一个领先的NoSQL数据库 是一个面向列存储的NoSQL数据库 是一个分布式Hash Map,底层数据是Key-Value格式 基于Coogle Big Table论文 使用HD…...

蓝桥杯错误记录
今天在做 小蜜蜂的综合案例的时候,数码管显示,有重影。 #include <STC15F2K60S2.H> unsigned char num; unsigned char code Duan[22]{0xc0,0xf9,0xa4,0xb0,0x99,0x92,0x82,0xf8,0x80,0x90,0x88,0x80, 0xc6,0xc0,0x86,0x8e,0xbf,0x7f,0XC1,0X8C,0…...

Spring-静态代理VS动态代理/实现代理ProxyFactory
文章目录 静态代理VS动态代理Spring实现代理ProxyFactory 工作中遇到问题整理动态代理异常com.sun.proxy.$Proxy0 cannot be cast to 静态代理VS动态代理 静态代理VS动态代理 参考URL: https://blog.csdn.net/qq_25881443/article/details/103245938 【java项目实战】代理模式…...
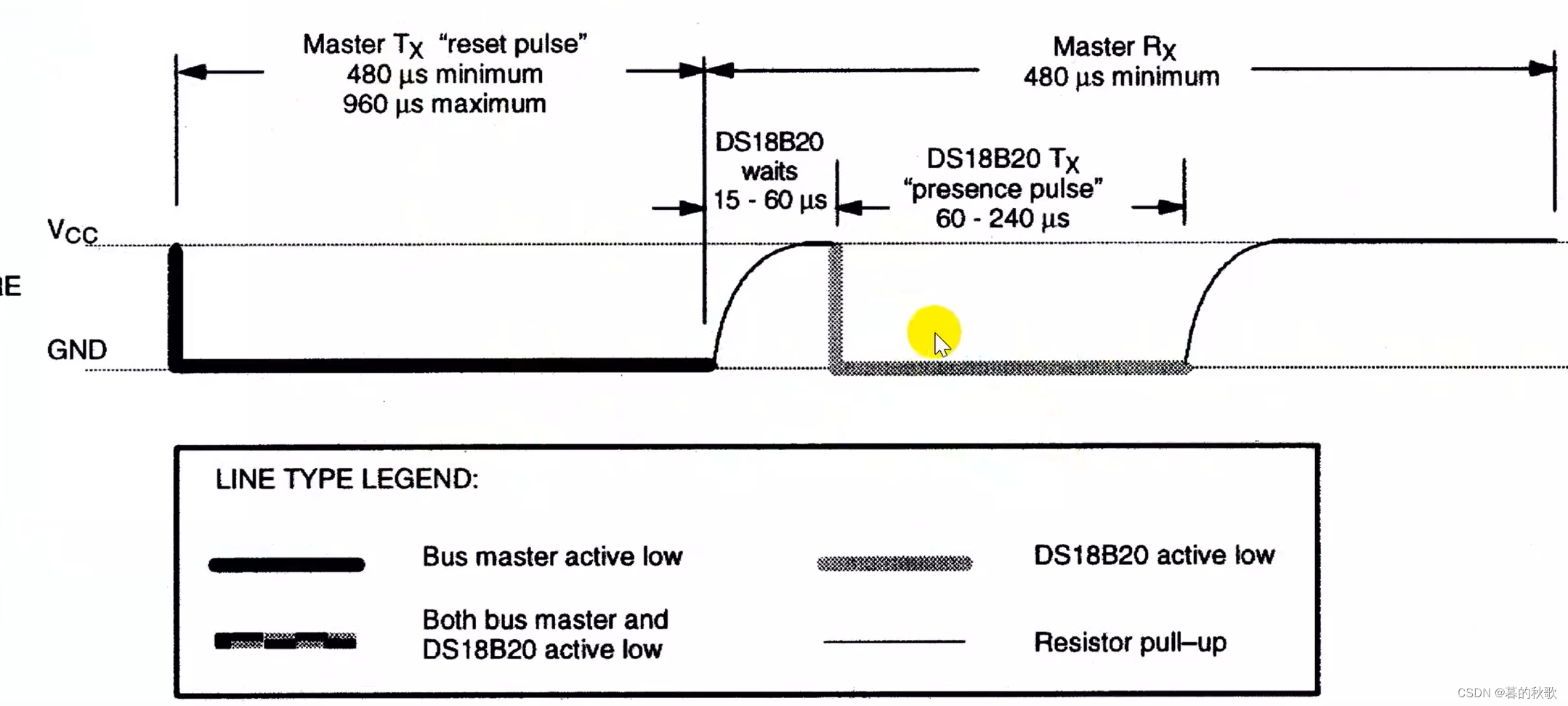
单片机精进之路-9ds18b20温度传感器
ds18b20复位时序图,先将b20的数据引脚拉低至少480us,然后再将数据引脚拉高15-60us,再去将测传感器的数据引脚是不是变低电平并保持60-240us,如果是,则说明检测到温度传感器,并正常工作。需要在240us后才能检…...
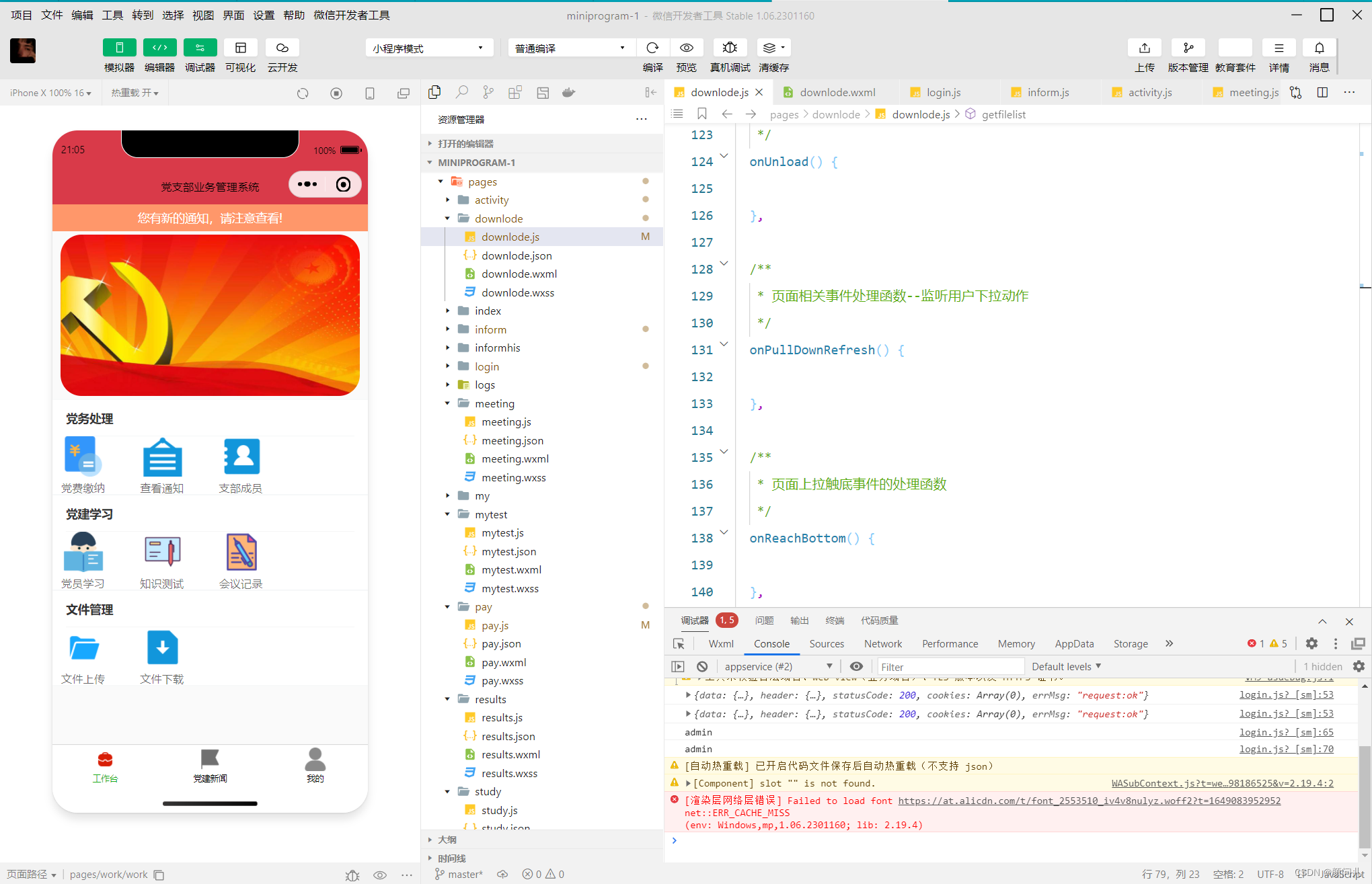
支部管理系统微信小程序(管理端+用户端)flask+vue+mysql+微信小程序
系统架构如图所示 高校D支部管理系统 由web端和微信小程序端组成,由web端负责管理,能够收缴费用、发布信息、发布问卷、发布通知等功能 部分功能页面如图所示 微信小程序端 包含所有源码和远程部署,可作为毕设课设...
)
4、Linux-常用命令(二)
目录 一、搜索命令 1、命令搜索命令 2、文件搜索命令find。格式:find [搜索范围] [搜索条件]。 3、字符串搜索命令grep 二、帮助命令 1、man【详细的帮助】 2、--help【简要的帮助】 三、压缩与解压命令 1、.zip格式 2、.gz格式 3、打包 四、关机和重启命…...

golang实现openssl自签名双向认证
第一步:生成CA、服务端、客户端证书 1. 生成CA根证书 生成CA证书私钥 openssl genrsa -out ca.key 4096创建ca.conf 文件 [ req ] default_bits 4096 distinguished_name req_distinguished_name[ req_distinguished_name ] countryName …...
【学习】torchvision.datasets.ImageFolder()
在分类任务中,数据集文件存储往往是如下形式: - train- class1- image1.jpg- image2.jpg...- class2- image1.jpg- image2.jpg......此时,我们想要获取图片和标签,标签即为文件名(class1、class2…) 可以使…...

pyinstaller打包的exe运行报错 No module named path
描述 用python开发了一个opc client应用,调试没有问题后,使用pyinstaller打包成exe,测试exe运行也没有问题,正常使用。 在某次重装win10系统后,在此运行exe就开始报错了,详细内容如下: ------…...
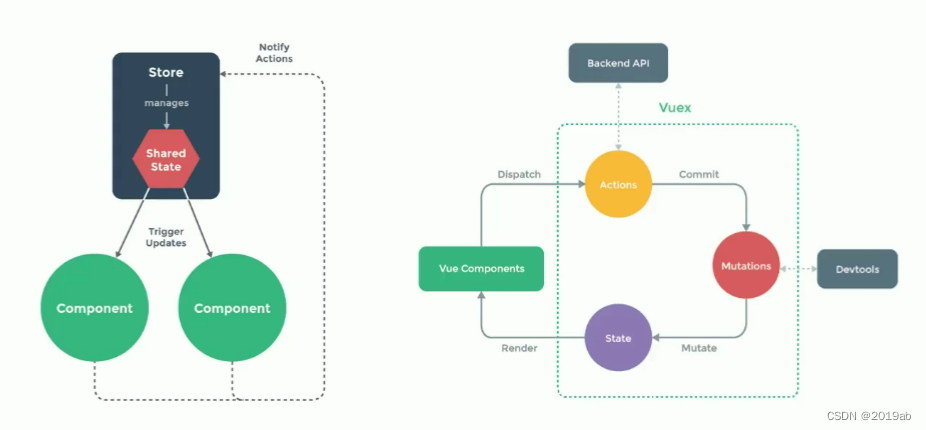
Vue3中Vuex状态管理库学习笔记
1.什么是状态管理 在开发中,我们会的应用程序需要处理各种各样的数据,这些数据需要保存在我们应用程序的某个位置,对于这些数据的管理我们就称之为状态管理。 在之前我们如何管理自己的状态呢? 在Vue开发中,我们使用…...

React富文本编辑器开发(二)
我们接着上一节的示例内容,现在有如下需求,我们希望当我们按下某个按键时编辑器有所反应。这就需要我们对编辑器添加事件功能onKeyDown, 我们给 Editor添加事件: SDocor.jsx import { useState } from react; import { createEditor } from…...
nginx代理minio客户端
错误方式 在点击桶名查看文件时, 会一直处于loading加载中 worker_processes 1; #设置 Nginx 启动的工作进程数为 1。events {worker_connections 1024; ##设置每个工作进程的最大并发连接数为 1024。 }http {include mime.types; #该文件定义了文件扩展名和 MIME 类型…...
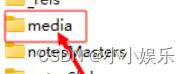
将ppt里的视频导出来
将ppt的后缀从pptx改为zip 找到【media】里面有存放图片和音频以及视频,看文件名后缀可以找到,mp4的即为视频,直接复制粘贴到桌面即可。 关闭压缩软件把ppt后缀改回,不影响ppt正常使用。...

Spring Boot 3核心技术与最佳实践
💂 个人网站:【 海拥】【神级代码资源网站】【办公神器】🤟 基于Web端打造的:👉轻量化工具创作平台💅 想寻找共同学习交流的小伙伴,请点击【全栈技术交流群】 highlight: a11y-dark 引言 Spring Boot作为…...
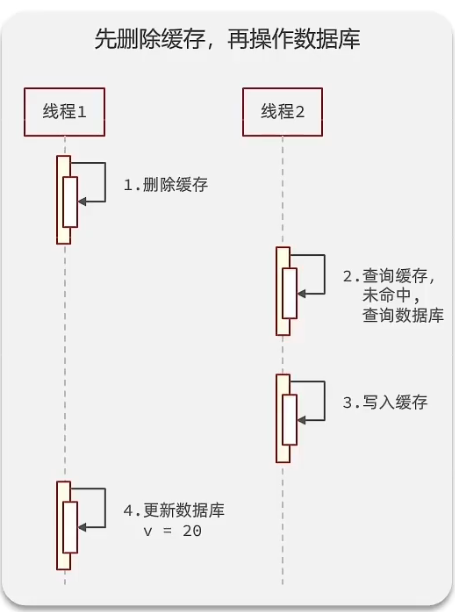
redis缓存更新策略
更新缓存策略: 对于低一致性需求的业务:使用redis自带的内存淘汰机制就行了,自动失效,等查询时再更新。 对于高一致性需求的业务:推荐主动更新,由缓存的调用者更新数据库的同时更新缓存(删除缓存)。 这里的…...

【操作系统学习笔记】文件管理1.4
【操作系统学习笔记】文件管理1.4 参考书籍: 王道考研 视频地址: Bilibili 文件的物理结构 文件快、磁盘块 在内存管理中,进程的逻辑空间被分为一个一个页面。同样的,在外存管理中,为了方便对文件数据的管理,文件的逻辑地址空…...

快递包装展|2024上海国际电商物流包装产业展览会
2024中国(上海)国际电商物流包装产业展览会 2024 China (Shanghai) international e-commerce logistics packaging industry exhibition 时 间:2024年7月24日 —7月26日 地 点:国家会展中心(上海市青浦区崧泽大道333号ÿ…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
