Python与FPGA——全局二值化
文章目录
- 前言
- 一、Python全局128
- 二、Python全局均值
- 三、Python全局OTSU
- 四、FPGA全局128
- 总结
前言
为什么要进行图像二值化,rgb图像有三个通道,处理图像的计算量较大,二值化的图像极大的减少了处理图像的计算量。即便从彩色图像转成了二值化图像,也不影响对物体的识别。本章开始讲解图像二值化。Python包含全局128、全局均值、大津阈值法(OTSU);FPGA只做全局128的讲解。
一、Python全局128
import numpy as np
import matplotlib.pyplot as plt
img = plt.imread("lenna.png")
gray = 0.299 * img[:, :, 0] + 0.587 * img[:, :, 1] + 0.114 * img[:, :, 2]
gray = gray * 255#图像是[0-1]--->[0-255]
bin_image = np.where(gray >= 128, 255, 0)#全局二值化
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(1, 2, 1)
ax.set_title("gray image")
ax.set_xlabel("width")
ax.set_ylabel("height")
plt.imshow(gray, cmap="gray")
ax = fig.add_subplot(1, 2, 2)
ax.set_title("binary image")
ax.set_xlabel("width")
ax.set_ylabel("height")
plt.imshow(bin_image, cmap="gray")

二、Python全局均值
mean_image = np.where(gray > np.mean(gray), 255, 0)#全局均值
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(1, 2, 1)
ax.set_title("gray image")
ax.set_xlabel("width")
ax.set_ylabel("height")
plt.imshow(gray, cmap="gray")
ax = fig.add_subplot(1, 2, 2)
ax.set_title("mean image")
ax.set_xlabel("width")
ax.set_ylabel("height")
plt.imshow(mean_image, cmap="gray")

三、Python全局OTSU
OTSU是阈值分割中一种常用的算法,它可以根据图像自动生成最佳分割阈值。 OTSU的核心思想是类间方差最大化。
- 初始化一个阈值T0,将图像分为前景f和背景b;
- 图像像素点个数为图像N=height x width,前景像素个数Nf,背景像素个数Nb;
- 图像灰度等级L-1(0~255=256),每个灰度等级像素个数Ni,满足以下公式:
P f = ∑ i = 0 i = T 0 N i N P b = ∑ i = T 0 i = L − 1 N i N (1) Pf = \sum_{i = 0}^{i=T0}\frac{Ni}{N} \quad\quad Pb= \sum_{i = T0}^{i=L-1}\frac{Ni}{N}\tag{1} Pf=i=0∑i=T0NNiPb=i=T0∑i=L−1NNi(1)
- 前景和背景的灰度平均值分别为:
M f = ∑ i = 0 i = T 0 i × P i P f M b = ∑ i = T 0 i = L − 1 i × P i P b (2) Mf = \sum_{i = 0}^{i=T0}i \times \frac{Pi}{Pf} \quad\quad Mb= \sum_{i = T0}^{i=L-1}i\times\frac{Pi}{Pb}\tag{2} Mf=i=0∑i=T0i×PfPiMb=i=T0∑i=L−1i×PbPi(2)
-
整个图像灰度平均值:
M = P f × M f + P b × M b (3) M = Pf \times Mf + Pb \times Mb\tag{3} M=Pf×Mf+Pb×Mb(3) -
求前景和背景之间的方差:
σ 2 = P f × ( M f − M ) 2 + P b × ( M b − M ) 2 (4) \sigma^2 = Pf\times(Mf-M)^2 + Pb \times(Mb-M)^2\tag{4} σ2=Pf×(Mf−M)2+Pb×(Mb−M)2(4) -
找到阈值T0,使得公式4最大;
-
怎么找?可以采用优化算法,本文中直接遍历灰度等级,查找最优阈值。
"""
统计像素点函数
image: 输入灰度图(ndarray)
reutrn: {像素:个数}(dict)
"""
def pixel_num(image):h, w = image.shapepdict = {}for i in range(h):for j in range(w):if image[i,j] in pdict:pdict[image[i,j]] += 1else:pdict[image[i,j]] = 0return pdict"""
求公式4中sigma2的值
T0: 预设阈值(int)
gray: 灰度图(ndarray)
L: 灰度等级(int)
"""
def sigma2(T0, gray, L=256):h, w = gray.shapeN = h * wpdict = pixel_num(gray)pf = sum([v for k,v in pdict.items() if k < T0]) / N#公式1pb = sum([v for k,v in pdict.items() if k >= T0]) / N#公式1pf = [pf if pf > 1e-6 else 1e-6][0]#控制最小值,避免除以0pb = [pb if pb > 1e-6 else 1e-6][0]#控制最小值,避免除以0mf = sum([k * pdict.get(k, 0) / N for k in range(T0)]) / pf#公式2mb = sum([k * pdict.get(k, 0) / N for k in range(T0, L)]) / pb#公式2M = pf * mf + pb * mb#公式3s2 = pf * (mf - M) ** 2 + pb * (mb - M) ** 2#公式4return s2, T0"""
遍历查找最大sigma2
gray: 灰度图(ndarray)
L: 灰度等级(int)
"""
def otsu(gray, L=256):smax = 0tmax = 0for t in range(1, L):s2, T0 = sigma2(t, gray, L)if s2 > smax:smax = s2tmax = T0return smax, tmax"""
根据最佳阈值求二值化图像
threshold: 最佳阈值(int)
return: 二值化图像(ndarray)
"""
def otsu_threshold(max_threshold, gray):threshold = np.mean(gray)binary = np.where(gray >= max_threshold, 255, 0)return binarysmax, tmax = otsu(gray, 256)
otsu_image = otsu_threshold(tmax, gray)
plt.figure(figsize=(10,10))
ax = plt.subplot(1, 2, 1)
ax.set_title("gray image")
ax.set_xlabel("width")
ax.set_ylabel("height")
plt.imshow(gray, cmap="gray")
ax = plt.subplot(1, 2, 2)
ax.set_title("otsu image")
ax.set_xlabel("width")
ax.set_ylabel("height")
plt.imshow(otsu_image, cmap="gray")

大津阈值法计算量较大,FPGA实现没有意义。
四、FPGA全局128
module ycbcr2binary_global
(input wire vga_clk ,input wire sys_rst_n ,input wire [7:0] y_data ,input wire rgb_valid ,output reg [15:0] binary_data
);
wire [7: 0] temp;
reg y_valid;
assign temp = (y_data >= 8'd128)? 8'd255: 8'd0; always @(posedge vga_clk or negedge sys_rst_n)if(sys_rst_n == 1'b0)y_valid <= 1'b0;elsey_valid <= rgb_valid;always@(posedge vga_clk or negedge sys_rst_n)if(sys_rst_n == 1'b0)binary_data <= 16'd0 ;else if(y_valid == 1'b1)binary_data <= {temp[7:3], temp[7:2], temp[7:3]};elsebinary_data <= binary_data;
endmodule

总结
全局二值化都比较基础,Python与FPGA实现都较为简单。下期讨论难度升级的局部二值化,敬请期待。
相关文章:

Python与FPGA——全局二值化
文章目录 前言一、Python全局128二、Python全局均值三、Python全局OTSU四、FPGA全局128总结 前言 为什么要进行图像二值化,rgb图像有三个通道,处理图像的计算量较大,二值化的图像极大的减少了处理图像的计算量。即便从彩色图像转成了二值化图…...

《Docker极简教程》--Docker的高级特性--Docker Compose的使用
Docker Compose是一个用于定义和运行多容器Docker应用程序的工具。它允许开发人员通过简单的YAML文件来定义应用程序的服务、网络和卷等资源,并使用单个命令来启动、停止和管理整个应用程序的容器。以下是关于Docker Compose的一些关键信息和优势: 定义…...

tidyverse去除表格中含有NA的行
在tidyverse中,特别是使用dplyr包,去除含有NA的行可以通过filter()函数结合is.na()和any()或all()函数来实现。dplyr是tidyverse的一部分,提供了一系列用于数据操作的函数,使数据处理变得更加简单和直观。 以下是一个简单的例子&…...
开源爬虫技术在金融行业市场分析中的应用与实战解析
一、项目介绍 在当今信息技术飞速发展的时代,数据已成为企业最宝贵的资产之一。特别是在${industry}领域,海量数据的获取和分析对于企业洞察市场趋势、优化产品和服务至关重要。在这样的背景下,爬虫技术应运而生,它能够高效地从互…...

使用SMTP javamail发送邮件
一、SMTP协议 SMTP(Simple Mail Transfer Protocol)即简单邮件传输协议,它是一组用于由源地址到目的地址传送邮件的规则,由它来控制信件的中转方式。SMTP协议属于TCP/IP协议簇,它帮助每台计算机在发送或中转信件时找到下一个目的地。使用javamail编写发送…...

Hello C++ (c++是什么/c++怎么学/c++推荐书籍)
引言 其实C基础语法基本上已经学完,早就想开始写C的博客了,却因为其他各种事情一直没开始。原计划是想讲Linux系统虚拟机安装的,后来考虑了一下还是算了,等Linux学到一定程度再开始相关博客的写作和发表吧。今天写博客想给C开个头…...

最新的前端开发技术(2024年)
关于作者: 还是大剑师兰特:曾是美国某知名大学计算机专业研究生,现为航空航海领域高级前端工程师;CSDN知名博主,GIS领域优质创作者,深耕openlayers、leaflet、mapbox、cesium,canvas࿰…...
GCN 翻译 - 2
2 FAST APROXIMATE CONVOLUTIONS ON GRAPHS 在这一章节,我们为这种特殊的的图基础的神经网络模型f(X, A)提供理论上的支持。我们考虑一个多层的图卷积网络(GCN),它通过以下方式进行层间的传播: 这里,是无…...
HBase 的安装与部署
目录 1 启动 zookeeper2 启动 Hadoop3 HBase 的安装与部署4 HBase 高可用 1 启动 zookeeper [huweihadoop101 ~]$ bin/zk_cluster.sh start2 启动 Hadoop [huweihadoop101 ~]$ bin/hdp_cluster.sh start3 HBase 的安装与部署 (1)将 hbase-2.0.5-bin.tar.…...

236.二叉搜索树的公共祖先
236.二叉树的公共祖先 思路 看到题想的是找到两个点的各自路径利用stack保存,根据路径长度大小将两个stack的值对齐到同一层,之后同时出栈节点,若相同则找到祖先节点。但是效率不高 看了大佬代码,递归思想很难理解。 根据大佬…...
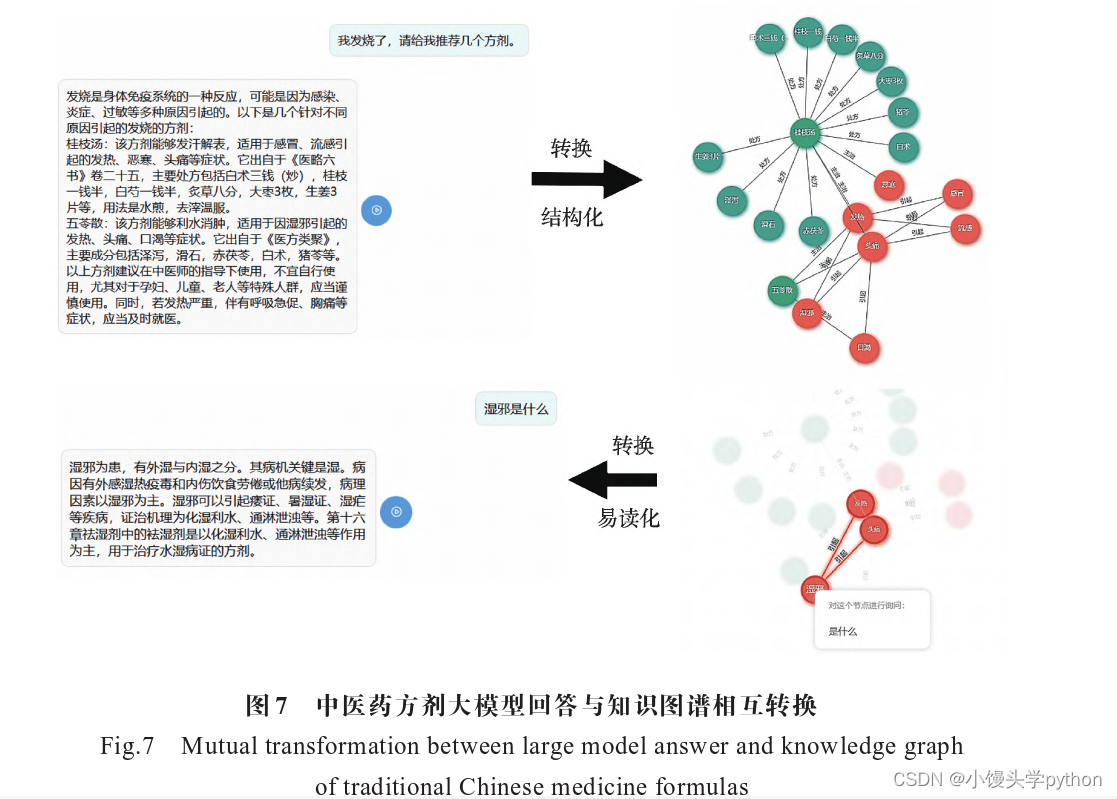
【论文精读】大语言模型融合知识图谱的问答系统研究
💗💗💗欢迎来到我的博客,你将找到有关如何使用技术解决问题的文章,也会找到某个技术的学习路线。无论你是何种职业,我都希望我的博客对你有所帮助。最后不要忘记订阅我的博客以获取最新文章,也欢…...
LabVIEW高精度天线自动测试系统
LabVIEW高精度天线自动测试系统 系统是一个集成了LabVIEW软件的自动化天线测试平台,提高天线性能测试的精度与效率。系统通过远程控制测试仪表,实现了数据采集、方向图绘制、参数计算等功能,特别适用于对天线辐射特性的精确测量。 在天线的…...
7.3 支付模块 - 创建订单、查询订单、通知
支付模块 - 创建订单、查询订单、通知 文章目录 支付模块 - 创建订单、查询订单、通知一、生成支付二维码1.1 数据模型1.1.1 订单表1.1.2 订单明细表1.1.3 支付交易记录表 1.2 执行流程1.3 Dto1.3.1 AddOrderDto 商品订单1.3.2 PayRecordDto支付交易记录扩展字段1.3.3 雪花算法…...

灵魂指针,教给(一)
欢迎来到白刘的领域 Miracle_86.-CSDN博客 系列专栏 C语言知识 先赞后看,已成习惯 创作不易,多多支持! 一、内存和地址 1.1 内存 在介绍知识之前,先来想一个生活中的小栗子: 假如把你放在一个有100间屋子的酒店…...
Linux 开发工具 yum、git、gdb
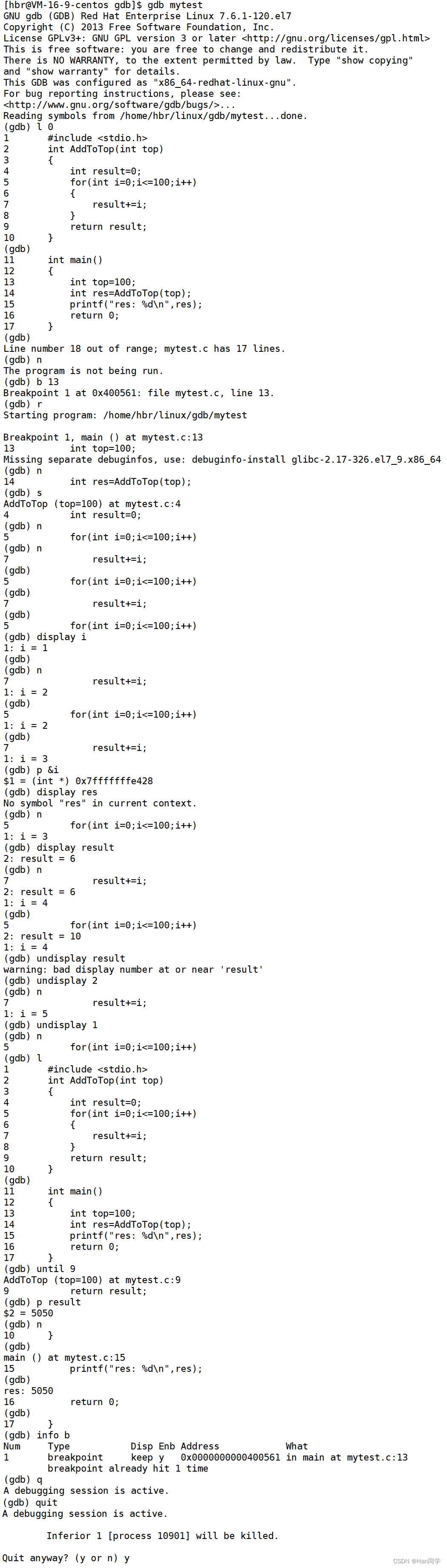
目录 一、yum 1、软件包 2、rzsz 3、注意事项 4、查看软件包 5、安装软件 6、卸载软件 二、git操作 1、克隆三板斧 2、第一次使用会出现以下情况: 未配置用户名和邮箱: push后弹出提示 三、gdb使用 1、背景 2、使用方法 例一:…...

Markdown
这里写自定义目录标题 欢迎使用Markdown编辑器 新的改变 功能快捷键 合理的创建标题,有助于目录的生成 如何改变文本的样式 插入链接与图片 如何插入一段漂亮的代码片 生成一个适合你的列表 创建一个表格 设定内容居中、居左、居右 SmartyPants 创建一个自定义列表 …...

【Oracle】oracle中sql给表新增字段并添加注释说明;mysql新增、修改字段
oracle中sql给表新增字段并添加注释说明 ALTER TABLE 表名 ADD 字段名 类型 COMMENT ON COLUMN 表面.字段名 IS ‘注释内容’ ALTER TABLE GROUP ADD T NUMBER(18) COMMENT ON COLUMN GROUP.T IS ‘ID’ mysql新增、修改字段、已有字段增加默认值 ALTER TABLE 表名 ADD COL…...

【汇总】pytest简易教程
pytest作为python技术栈里面主流、火热的技术,非常有必要好好学一下,因为工作和面试都能用上; 它不仅简单易用,还很强大灵活,重点掌握fixture、parametrize参数化、allure-pytest插件等,这些在后续自动化框…...

openssl调试记录
openssl不能直接解密16进制密文,需要把密文转化成base64格式才能解密 调试记录如下:...

3.7练习题解
一共五道题: 1. PERKET: 观察容易发现n的值很小,所以我们可以考虑使用dfs的方法进行解答,首先我们可以考虑一共有n种配料,那么我们就可以考虑到可以选择1到n种配料数目,然后基于这个思路我们再对其进行判断…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
