3.7练习题解
一共五道题:
1. PERKET:

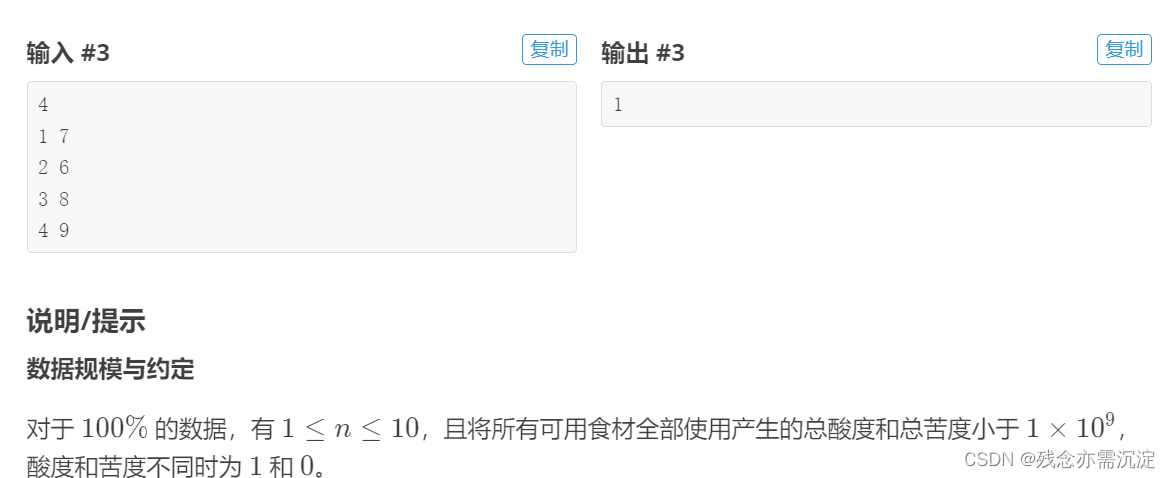
观察容易发现n的值很小,所以我们可以考虑使用dfs的方法进行解答,首先我们可以考虑一共有n种配料,那么我们就可以考虑到可以选择1到n种配料数目,然后基于这个思路我们再对其进行判断当选择几种并且选择哪几种能够得到最小的酸甜度匹配,于是代码就如下:
#include<bits/stdc++.h>
using namespace std;
const int N=50;
int n,ans=1<<20,x=1,y=0;
int a[N],b[N],book[N];
void dfs(int c){if(c==0){ans=min(ans,abs(x-y));return;} for(int i=1;i<=n;i++){if(book[i]){x*=a[i];y+=b[i];--c;book[i]=0;dfs(c);book[i]=1;++c;x/=a[i];y-=b[i];}}
}
int main(){ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin>>n;for(int i=1;i<=n;i++){cin>>a[i]>>b[i];}for(int i=1;i<=n;i++){x*=a[i];y+=b[i];}ans=min(ans,abs(x-y));for(int i=1;i<=n;i++){ans=min(ans,abs(a[i]-b[i]));}for(int i=2;i<n;i++){memset(book,1,sizeof(book));x=1;y=0;dfs(i);}cout<<ans<<endl;return 0;
}引入了book数组来标记在dfs过程中已经被使用过的配料,然后先把选择一种和n种配料的情况给算出来并更新最小的ans,接下来再判断当选择的配料数目为2到n-1的时候,对应的最小ans,并利用dfs进行不断更新。
2.迷宫:

这道题目就是最经典和典型的dfs模板题目了,直接上代码吧:
#include<iostream>
#include<cstring>
using namespace std;
int n,m,t;
int startx,starty,p,q;
const int N=10;
int book[50][50],a[50][50];
int ans=0;
void dfs(int x,int y){if(x==p && y==q){++ans;return;} int next[4][2]={{0,1},{1,0},{0,-1},{-1,0}};int tx,ty;for(int i=0;i<=3;i++){tx=x+next[i][0];ty=y+next[i][1];if(tx < 1 || tx > n || ty < 1 || ty > m)continue;if(!book[tx][ty] && a[tx][ty]){book[tx][ty] = 1;dfs(tx,ty);if(a[tx][ty]) book[tx][ty]=0;}}
}
int main(){cin >> n >> m >> t;cin >> startx >> starty >> p >> q;memset(book,0,sizeof(book));for(int i=1;i<=n;i++){for(int j=1;j<=m;j++)a[i][j]=1;}for(int i=1;i<=t;i++){int x,y;cin>>x>>y;a[x][y]=0;}dfs(startx,starty);cout<<ans<<endl;return 0;
}利用一个a数组代表是否有陷阱,利用book数组表示对于同一种方案是否有走过同一个格子,在dfs中利用一个二维数组来表示接下来一步的上下左右并进行枚举,不过我至今没有想明白为什么这只能获得70分。
3.借教室:


#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1000010;
int n, m;
int w[N];//这个数组用来存储n天中每一天对应的可借出去的教室
int l[N], r[N], d[N];//l和r分别表示对应天数的差分端点,d数组则表示对应需要借出的教室
LL b[N];//当进行二分筛选的时候这一个数组就是拿来进行记录当订单数量为mid的时候每一天需要的教室数量
bool check(int mid)
{memset(b, 0, sizeof b);for (int i = 1; i <= mid; i ++ ){b[l[i]] += d[i];b[r[i] + 1] -= d[i];//对端点进行加减}for (int i = 1; i <= n; i ++ ){b[i] += b[i - 1];if (b[i] > w[i]) return false;//如果当天的需求大于所能提供的教室数量则说明要求的值在mid的左边}return true;
}
int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++ )scanf("%d", &w[i]);for (int i = 1; i <= m; i ++ )scanf("%d%d%d", &d[i], &l[i], &r[i]);int l = 0, r = m;while (l < r){int mid = l + r + 1 >> 1;//我们的二分求出来的r是最后一份能恰好满足教室需求的订单,r+1则是第一个无法满足的订单,记得右移if (check(mid)) l = mid;else r = mid - 1;}if (r == m) puts("0");else printf("-1\n%d\n", r + 1);return 0;
}这道题目的方法就是差分加二分,订单的数量越多,那么剩余的空余教室的数量肯定会减少,因此我们考虑使用二分的方法进行查找,对于每一份订单,我们都有一个区间,在这个区间上加上订单所对应的借教室的数量,但是我们会发现题目当中,n和m的极限数据是10的6次方,如果对于每一个订单我们都将从第l天到第r天进行枚举并加上借教室的数量的话会导致tle,所以我们考虑使用差分的方式进行加速处理,这样处理的时间复杂度为O(n+m)logm。
以下是二分的两种模板:
bool check(int x) {/* ... */} // 检查x是否满足某种性质// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r)
{while (l < r){int mid = l + r >> 1;if (check(mid)) r = mid; // check()判断mid是否满足性质else l = mid + 1;}return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
int bsearch_2(int l, int r)
{while (l < r){int mid = l + r + 1 >> 1;if (check(mid)) l = mid;else r = mid - 1;}return l;
}4.分巧克力:

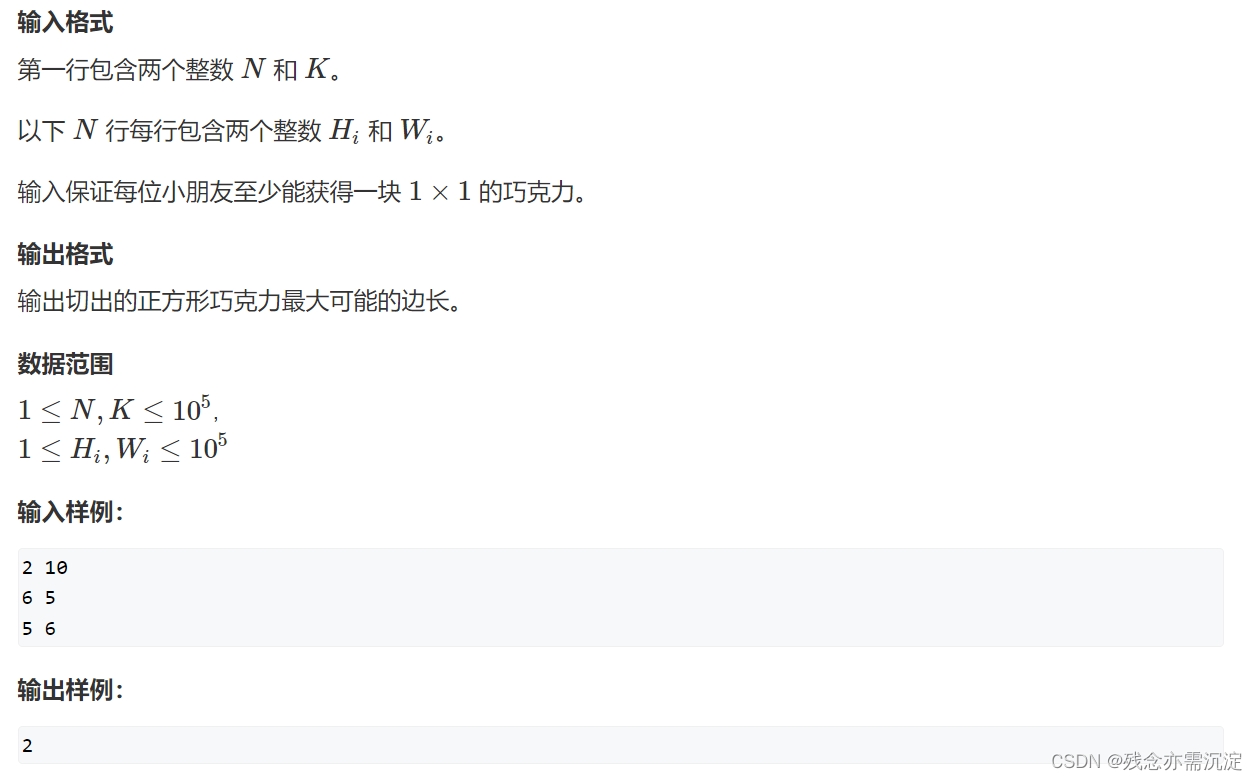 这道题目的话 难度比排教室要小很多了,我们可以考虑使用二分来找到所给的巧克力总共可以分成的边长最大的数量大于k的答案,那么我们的代码可以这样去写:
这道题目的话 难度比排教室要小很多了,我们可以考虑使用二分来找到所给的巧克力总共可以分成的边长最大的数量大于k的答案,那么我们的代码可以这样去写:
#include<iostream>
using namespace std;
const int N=1e5+100;
int w[N],h[N];
int n,k;
bool pd(int x){int ans=0;for(int i=1;i<=n;i++){ans += (w[i]/x) * (h[i]/x);}if(ans>=k) return true;else return false;
}
int main(){cin>>n>>k;for(int i=1;i<=n;i++){cin>>w[i]>>h[i];}int l=1,r=100000;while(l<r){int mid=l+r+1>>1;if(pd(mid)) l=mid;else r=mid-1;}cout<<r<<endl;return 0;
}5.技能升级

这是一道很难的题目,题解如下:



一定要记得开long long:
#include <iostream>
#include <cmath>
#define N 100005
using namespace std;
int n, m, l = 0, r = 1e6, mid, now, cnt, a[N], b[N];
long long ans;
long long sum (int r, int n, int t) // 求和
{int l = r - t * (n - 1);return (long long) (l + r) * n >> 1;
}
bool check (int x)
{long long res = 0;for (int i = 1; i <= n; i ++){if (a[i] > x) // 前提条件{res += ceil ((double) (a[i] - x) / b[i]);// 累计第 i 个技能发动的次数}}return res <= m; // 判断是否合法
}
int main ()
{cin >> n >> m;for (int i = 1; i <= n; i ++){cin >> a[i] >> b[i];}while (l < r) // 二分{mid = l + r >> 1;if (check (mid)) // 如果 x = mid 合法{r = mid;}else{l = mid + 1;}}for (int i = 1; i <= n; i ++){if (a[i] > l) // 前提条件{now = ceil ((double) (a[i] - l) / b[i]), cnt += now;// now 是第 i 个技能发动的次数,cnt 则是总共升级了多少次ans += sum (a[i], now, b[i]);// 总升级攻击力累加上右端点为 a[i],项数为 now,公差为 b[i] 的等差数列和}}cout << ans + (long long) l * (m - cnt); // 答案还要记得加上那些等于 l 的攻击力增加return 0;
}感谢您的观看。
相关文章:

3.7练习题解
一共五道题: 1. PERKET: 观察容易发现n的值很小,所以我们可以考虑使用dfs的方法进行解答,首先我们可以考虑一共有n种配料,那么我们就可以考虑到可以选择1到n种配料数目,然后基于这个思路我们再对其进行判断…...

MQ的消费模式-消息是推还是拉
文章目录 概述RocketMQ默认pushRabbitMQ默认pushKafka默认拉PullActiveMQ默认push 概述 MQ的消费模式可以大致分为两种,一种是推Push,一种是拉Pull Push是服务端主动推送消息给客户端,Pull是客户端需要主动到服务端轮询获取数据。 推优点是及…...
一个平台满足你对测试工具的所有需求
背景 目前,测试人员普遍使用的测试工具有Postman、JMeter等,但这些工具都存在一定的局限性。例如,Postman缺少对API性能测试方面的支持,而JMeter则缺乏一个整合测试报告、测试脚本的统一管理系统以及UI测试功能。 RunnerGo是什么…...

【C语言】【字符串函数】【超详解】【上】!!!
前言: 在学习C语言的过程中,字符串、字符数组等对新手来说总是会有疏忽,在已有的库函数中,我们平时用到最多的就是关于字符串的函数,今天我们就来详细学习字符串函数的相关内容。 下面我们就开始讲解字符串函数&#x…...

算法沉淀——动态规划之其它背包问题与卡特兰数(leetcode真题剖析)
算法沉淀——动态规划之其它背包问题与卡特兰数 二维费用的背包问题01.一和零02.盈利计划 似包非包组合总和 Ⅳ 卡特兰数不同的二叉搜索树 二维费用的背包问题 01.一和零 题目链接:https://leetcode.cn/problems/ones-and-zeroes/ 给你一个二进制字符串数组 strs…...

selenium中ChromeDriver配置,一把过,并且教你伪装
最近正值毕业季,我之前不是写了个问卷星代码嘛,昨晚上有人凌晨1点加我,问我相关内容。 由于我之前C盘重装了一下,导致我很多东西空有其表,实际不能用,借此机会,向大家编写ChromeDriver配置&…...
vue3 + vite 项目可以使用纯Js开发吗?
答案:可以 创建项目: 按照链接参考或者按官方: webstorm 创建vue3 vite 项目-CSDN博客 项目目录 tsconfig.json 配置允许js allowJs指定是否编译js文件,在任意文件当中,如果我们模块使用js写的,那么我们需要 将all…...
Java EE之线程安全问题
一.啥是线程安全问题 有些代码,在单个线程执行时完全正确,但同样的代码让多个线程同时执行,就会出现bug。例如以下代码: 给定一个变量count,让线程t1 t2分别自增5000次,然后进行打印,按理说co…...

掌握Nodejs高级图片压缩技巧提升web优化
掌握Nodejs高级图片压缩技巧提升web优化 在当今的数字时代,图像在网络开发中发挥着至关重要的作用。它们增强视觉吸引力、传达信息并吸引用户。然而,高质量的图像通常有一个显着的缺点——较大的文件大小会减慢网页加载时间。为了应对这一挑战并确保快速加载网站,掌握 Node…...
C++初阶 类(上)
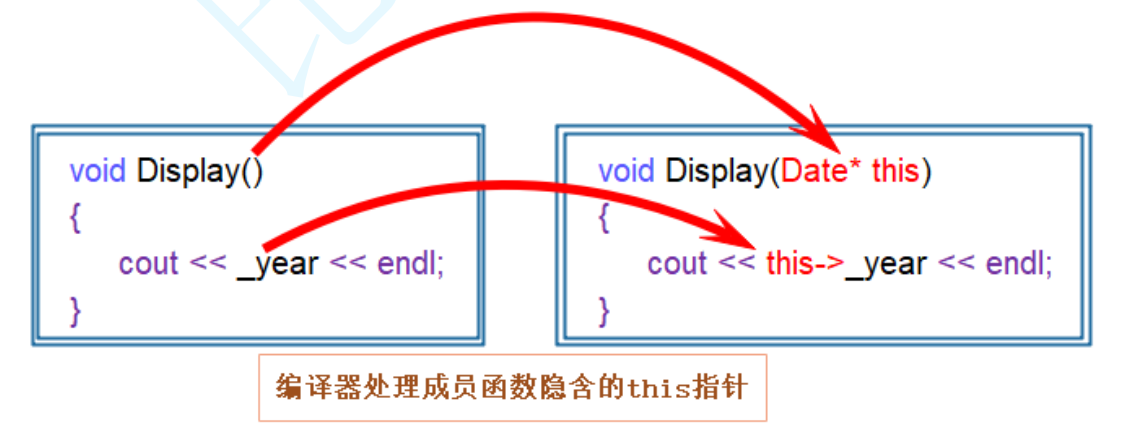
目录 1. 什么是类 2. 如何定义出一个类 3. 类的访问限定符 4. 类的作用域 5. 类的实例化 6. 类的大小 7. this指针 1.this指针的引出 2. this指针的特性 8. 面试题 1. 什么是类 在C语言中,不同类型的数据集合体是结构体。为了方便管理结构体,我…...

图片速览 BitNet: 1-bit LLM
输入数据 模型使用absmax 量化方法进行b比特量化,将输入量化到 [ − Q b , Q b ] ( Q b 2 b − 1 ) \left[-Q_{b},Q_{b}\right](Q_{b}2^{b-1}) [−Qb,Qb](Qb2b−1) x ~ Q u a n t ( x ) C l i p ( x Q b γ , − Q b ϵ , Q b − ϵ ) , Clip ( x , a , b ) ma…...

金融基础——拨备前利润和拨备后利润介绍
一、简介 拨备前利润(PreProvision Operating Profit,也就是PPOP)和拨备后利润的主要区别在于是否扣除减值准备金、是否遵循保守性原则以及显示的利润数值不同。 拨备前利润。指在计算利润时没有扣除减值准备金的利润,它等于税前…...
网络编程作业day7
作业项目:基于UDP的聊天室 服务器代码: #include <myhead.h>//定义客户信息结构体 typedef struct magtye {char type; //消息类型char name[100]; //客户姓名char text[1024]; //客户发送聊天信息 }msg_t;//定义结构体存储…...

【Vision Pro杀手级应用】3D音乐会/演唱会,非VR视频播放的形式,而是实实在在的明星“全息”形象,在你的面前表演
核心内容形式:体积视频 参考对标案例深度解读: 体积视频,这一全新的内容形式,正在引领我们进入一个前所未有的四维体验时代。它将传统的演艺形式推向了新的高度,让我们能够更加深入地沉浸在虚拟世界中,感受前所未有的视听盛宴。 在这一领域,有一个引人注目的案例,那…...

变频器学习
西门子变频器 SINAMICS V20 入门级变频器 SINAMICS G120C...
Linux Ubuntu系统安装MySQL并实现公网连接本地数据库【内网穿透】
文章目录 前言1 .安装Docker2. 使用Docker拉取MySQL镜像3. 创建并启动MySQL容器4. 本地连接测试4.1 安装MySQL图形化界面工具4.2 使用MySQL Workbench连接测试 5. 公网远程访问本地MySQL5.1 内网穿透工具安装5.2 创建远程连接公网地址5.3 使用固定TCP地址远程访问 前言 本文主…...

0048__Unix传奇
Unix传奇 (上篇)_unix传奇(上篇)-CSDN博客 Unix传奇 (下篇)-CSDN博客 Unix现状与未来——CSDN对我的采访_nuix邮件系统行业地位-CSDN博客...

蓝桥杯-排序
数组排序 Arrays.sort(int[] a) 这种形式是对一个数组的所有元素进行排序,并且时按从小到大的顺序。 package Work;import java.util.*;public class Imcomplete {public static void main(String args[]) {int arr[]new int [] {1,324,4,5,7,2};Arrays.sort(arr)…...
计算机设计大赛 深度学习的视频多目标跟踪实现
文章目录 1 前言2 先上成果3 多目标跟踪的两种方法3.1 方法13.2 方法2 4 Tracking By Detecting的跟踪过程4.1 存在的问题4.2 基于轨迹预测的跟踪方式 5 训练代码6 最后 1 前言 🔥 优质竞赛项目系列,今天要分享的是 基于深度学习的视频多目标跟踪实现 …...

高性能JSON框架之FastJson的简单使用
高性能JSON框架之FastJson的简单使用、 1.前言 1.1.FastJson的介绍: JSON协议使用方便,越来越流行,JSON的处理器有很多,这里我介绍一下FastJson,FastJson是阿里的开源框架,被不少企业使用,是一个极其优秀的Json框架,Github地址: FastJson 1.2.FastJson的特点: 1.F…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...

初探用uniapp写微信小程序遇到的问题及解决(vue3+ts)
零、关于开发思路 (一)拿到工作任务,先理清楚需求 1.逻辑部分 不放过原型里说的每一句话,有疑惑的部分该问产品/测试/之前的开发就问 2.页面部分(含国际化) 整体看过需要开发页面的原型后,分类一下哪些组件/样式可以复用,直接提取出来使用 (时间充分的前提下,不…...

【大厂机试题+算法可视化】最长的指定瑕疵度的元音子串
题目 开头和结尾都是元音字母(aeiouAEIOU)的字符串为元音字符串,其中混杂的非元音字母数量为其瑕疵度。比如: “a” 、 “aa”是元音字符串,其瑕疵度都为0 “aiur”不是元音字符串(结尾不是元音字符) “…...

leetcode 386. 字典序排数 中等
给你一个整数 n ,按字典序返回范围 [1, n] 内所有整数。 你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。 示例 1: 输入:n 13 输出:[1,10,11,12,13,2,3,4,5,6,7,8,9]示例 2: 输入:n 2…...

【Redis】数据库与缓存一致性
目录 1、背景2、核心问题3、常见解决方案【1】缓存更新策略[1]旁路缓存模式(Cache-Aside)[2]写穿透模式(Write-Through)[3]写回模式 【2】删除与更新策略[1]先更新数据库再删除缓存[2]先删除缓存再更新数据库 【3】一致性保障机制…...
