算法沉淀——动态规划之其它背包问题与卡特兰数(leetcode真题剖析)

算法沉淀——动态规划之其它背包问题与卡特兰数
- 二维费用的背包问题
- 01.一和零
- 02.盈利计划
- 似包非包
- 组合总和 Ⅳ
- 卡特兰数
- 不同的二叉搜索树
二维费用的背包问题
01.一和零
题目链接:https://leetcode.cn/problems/ones-and-zeroes/
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
输入:strs = ["10", "0", "1"], m = 1, n = 1
输出:2
解释:最大的子集是 {"0", "1"} ,所以答案是 2 。
提示:
1 <= strs.length <= 6001 <= strs[i].length <= 100strs[i]仅由'0'和'1'组成1 <= m, n <= 100
思路
问题转化为二维费用的01背包问题:
- 状态表示:
dp[i][j][k]表示从前i个字符串中挑选,字符0的个数不超过j,字符1的个数不超过k,所有的选法中,最大的长度。
- 状态转移方程:
- 根据最后一步的状况,分两种情况讨论:
- 不选第
i个字符串:相当于去前i - 1个字符串中挑选,并且字符0的个数不超过j,字符1的个数不超过k。此时的最大长度为dp[i][j][k] = dp[i - 1][j][k]。 - 选择第
i个字符串:接下来在前i - 1个字符串中挑选,字符0的个数不超过j - a,字符1的个数不超过k - b的最大长度,然后在这个长度后面加上字符串i。此时dp[i][j][k] = dp[i - 1][j - a][k - b] + 1。需要特判这种状态是否存在。
- 不选第
- 综上,状态转移方程为:
dp[i][j][k] = max(dp[i][j][k], dp[i - 1][j - a][k - b] + 1)。
- 根据最后一步的状况,分两种情况讨论:
- 初始化:
- 当没有字符串的时候,没有长度,因此初始化为
0。
- 当没有字符串的时候,没有长度,因此初始化为
- 填表顺序:
- 保证第一维的循环从小到大即可。
- 返回值:
- 根据状态表示,返回
dp[l][m][n]。
- 根据状态表示,返回
代码
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {int l=strs.size();vector<vector<vector<int>>> dp(l+1,vector<vector<int>>(m+1,vector<int>(n+1)));for(int i=1;i<=l;i++){int a=0,b=0;for(char ch:strs[i-1])if(ch=='0') a++;else b++;for(int j=m;j>=0;j--)for(int k=n;k>=0;k--){dp[i][j][k]=dp[i-1][j][k];if(j>=a&&k>=b) dp[i][j][k]=max(dp[i][j][k],dp[i-1][j-a][k-b]+1);}}return dp[l][m][n];}
};
02.盈利计划
题目链接:https://leetcode.cn/problems/profitable-schemes/
集团里有 n 名员工,他们可以完成各种各样的工作创造利润。
第 i 种工作会产生 profit[i] 的利润,它要求 group[i] 名成员共同参与。如果成员参与了其中一项工作,就不能参与另一项工作。
工作的任何至少产生 minProfit 利润的子集称为 盈利计划 。并且工作的成员总数最多为 n 。
有多少种计划可以选择?因为答案很大,所以 返回结果模 10^9 + 7 的值。
示例 1:
输入:n = 5, minProfit = 3, group = [2,2], profit = [2,3]
输出:2
解释:至少产生 3 的利润,该集团可以完成工作 0 和工作 1 ,或仅完成工作 1 。
总的来说,有两种计划。
示例 2:
输入:n = 10, minProfit = 5, group = [2,3,5], profit = [6,7,8]
输出:7
解释:至少产生 5 的利润,只要完成其中一种工作就行,所以该集团可以完成任何工作。
有 7 种可能的计划:(0),(1),(2),(0,1),(0,2),(1,2),以及 (0,1,2) 。
提示:
1 <= n <= 1000 <= minProfit <= 1001 <= group.length <= 1001 <= group[i] <= 100profit.length == group.length0 <= profit[i] <= 100
思路
- 状态表示:
dp[i][j][k]表示从前i个计划中挑选,总人数不超过j,总利润至少为k,有多少种选法。
- 状态转移方程:
- 根据最后一位的元素,有两种选择策略:
- 不选第
i位置的计划:此时只能在前i - 1个计划中挑选,总人数不超过j,总利润至少为k。此时有dp[i - 1][j][k]种选法。 - 选择第
i位置的计划:在前i - 1个计划中挑选的限制变成了,总人数不超过j - g[i],总利润至少为max(0, k - p[i])。此时有dp[i - 1][j - g[i]][max(0, k - p[i])]种选法。
- 不选第
- 注意特殊情况:
- 如果
j - g[i] < 0,说明人数过多,状态不合法,舍去。 - 对于
k - p[i] < 0,说明利润太高,但问题要求至少为k,因此将其取max(0, k - p[i])。
- 如果
- 综上,状态转移方程为:
dp[i][j][k] = dp[i - 1][j][k] + dp[i - 1][j - g[i]][max(0, k - p[i])]。
- 根据最后一位的元素,有两种选择策略:
- 初始化:
- 当没有任务时,利润为
0。在这种情况下,无论人数限制为多少,都能找到一个「空集」的方案。因此初始化dp[0][j][0]为1,其中0 <= j <= n。
- 当没有任务时,利润为
- 填表顺序:
- 根据状态转移方程,保证
i从小到大即可。
- 根据状态转移方程,保证
- 返回值:
- 根据状态表示,返回
dp[l][m][n],其中l表示计划数组的长度。
- 根据状态表示,返回
代码
class Solution {const int MOD=1e9+7;
public:int profitableSchemes(int n, int m, vector<int>& group, vector<int>& profit) {int l = group.size();vector<vector<vector<int>>> dp(l+1,vector<vector<int>>(n+1,vector<int>(m+1)));for(int j=0;j<=n;j++) dp[0][j][0]=1;for(int i=1;i<=l;i++)for(int j=0;j<=n;j++)for(int k=0;k<=m;k++){dp[i][j][k]=dp[i-1][j][k];if(j>=group[i-1]) dp[i][j][k]+=dp[i-1][j-group[i-1]][max(0,k-profit[i-1])];dp[i][j][k]%=MOD;}return dp[l][n][m];}
};
似包非包
组合总和 Ⅳ
题目链接:https://leetcode.cn/problems/combination-sum-iv/
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。
示例 1:
输入:nums = [1,2,3], target = 4
输出:7
解释:
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意,顺序不同的序列被视作不同的组合。
示例 2:
输入:nums = [9], target = 3
输出:0
提示:
1 <= nums.length <= 2001 <= nums[i] <= 1000nums中的所有元素 互不相同1 <= target <= 1000
思路
注意这里题目意思容易混淆概念,其实这里是一个排列问题而并非组合问题,所以应该是普通的动态规划问题
- 状态表示:
dp[i]表示总和为i时,一共有多少种排列方案。
- 状态转移方程:
- 对于
dp[i],根据最后一个位置划分,选择数组中的任意一个数nums[j],其中0 <= j <= n - 1。 - 当
nums[j] <= i时,排列数等于先找到i - nums[j]的方案数,然后在每一个方案后面加上一个数字nums[j]。 - 因为有很多个
j符合情况,状态转移方程为:dp[i] += dp[i - nums[j]],其中0 <= j <= n - 1。
- 对于
- 初始化:
- 当和为
0时,我们可以什么都不选,即「空集」一种方案,因此dp[0] = 1。
- 当和为
- 填表顺序:
- 根据状态转移方程,从左往右填表。
- 返回值:
- 根据状态表示,返回
dp[target]的值。
- 根据状态表示,返回
代码
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<double> dp(target+1);dp[0]=1;for(int i=1;i<=target;i++)for(int& x:nums)if(x<=i) dp[i]+=dp[i-x];return dp[target];}
};
卡特兰数
不同的二叉搜索树
题目链接:https://leetcode.cn/problems/unique-binary-search-trees/
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
输入:n = 3
输出:5
示例 2:
输入:n = 1
输出:1
提示:
1 <= n <= 19
思路
- 状态表示:
dp[i]表示当结点数量为i个时,一共有多少颗 BST。
- 状态转移方程:
- 对于
dp[i],选择每一个结点j作为头结点,分析不同头结点的 BST 数量。 - 根据 BST 的定义,
j号结点的左子树的结点编号在[1, j-1]之间,有j-1个结点,右子树的结点编号在[j+1, i]之间,有i-j个结点。 - 因此,
j号结点作为头结点的 BST 种类数量为dp[j-1] * dp[i-j]。 - 综合每一个可能的头结点,状态转移方程为:
dp[i] += dp[j-1] * dp[i-j],其中1 <= j <= i。
- 对于
- 初始化:
dp[0]表示空树,也是一颗二叉搜索树,因此dp[0] = 1。- 针对
i从 1 开始的情况,需要通过dp[j-1] * dp[i-j]来计算。
- 填表顺序:
- 从左往右填表,保证每一步都有所依赖的子问题的解。
- 返回值:
- 返回
dp[n]的值,表示结点数量为n时的 BST 种类数量。
- 返回
代码
class Solution {
public:int numTrees(int n) {vector<int> dp(n+1);dp[0]=1;for(int i=1;i<=n;i++)for(int j=1;j<=i;j++)dp[i]+=dp[j-1]*dp[i-j];return dp[n];}
};
相关文章:

算法沉淀——动态规划之其它背包问题与卡特兰数(leetcode真题剖析)
算法沉淀——动态规划之其它背包问题与卡特兰数 二维费用的背包问题01.一和零02.盈利计划 似包非包组合总和 Ⅳ 卡特兰数不同的二叉搜索树 二维费用的背包问题 01.一和零 题目链接:https://leetcode.cn/problems/ones-and-zeroes/ 给你一个二进制字符串数组 strs…...

selenium中ChromeDriver配置,一把过,并且教你伪装
最近正值毕业季,我之前不是写了个问卷星代码嘛,昨晚上有人凌晨1点加我,问我相关内容。 由于我之前C盘重装了一下,导致我很多东西空有其表,实际不能用,借此机会,向大家编写ChromeDriver配置&…...
vue3 + vite 项目可以使用纯Js开发吗?
答案:可以 创建项目: 按照链接参考或者按官方: webstorm 创建vue3 vite 项目-CSDN博客 项目目录 tsconfig.json 配置允许js allowJs指定是否编译js文件,在任意文件当中,如果我们模块使用js写的,那么我们需要 将all…...
Java EE之线程安全问题
一.啥是线程安全问题 有些代码,在单个线程执行时完全正确,但同样的代码让多个线程同时执行,就会出现bug。例如以下代码: 给定一个变量count,让线程t1 t2分别自增5000次,然后进行打印,按理说co…...

掌握Nodejs高级图片压缩技巧提升web优化
掌握Nodejs高级图片压缩技巧提升web优化 在当今的数字时代,图像在网络开发中发挥着至关重要的作用。它们增强视觉吸引力、传达信息并吸引用户。然而,高质量的图像通常有一个显着的缺点——较大的文件大小会减慢网页加载时间。为了应对这一挑战并确保快速加载网站,掌握 Node…...
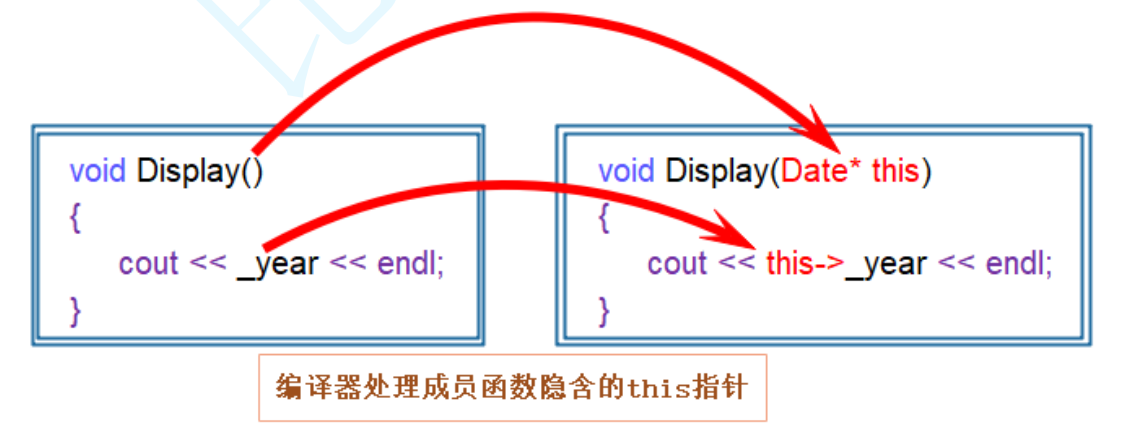
C++初阶 类(上)
目录 1. 什么是类 2. 如何定义出一个类 3. 类的访问限定符 4. 类的作用域 5. 类的实例化 6. 类的大小 7. this指针 1.this指针的引出 2. this指针的特性 8. 面试题 1. 什么是类 在C语言中,不同类型的数据集合体是结构体。为了方便管理结构体,我…...

图片速览 BitNet: 1-bit LLM
输入数据 模型使用absmax 量化方法进行b比特量化,将输入量化到 [ − Q b , Q b ] ( Q b 2 b − 1 ) \left[-Q_{b},Q_{b}\right](Q_{b}2^{b-1}) [−Qb,Qb](Qb2b−1) x ~ Q u a n t ( x ) C l i p ( x Q b γ , − Q b ϵ , Q b − ϵ ) , Clip ( x , a , b ) ma…...

金融基础——拨备前利润和拨备后利润介绍
一、简介 拨备前利润(PreProvision Operating Profit,也就是PPOP)和拨备后利润的主要区别在于是否扣除减值准备金、是否遵循保守性原则以及显示的利润数值不同。 拨备前利润。指在计算利润时没有扣除减值准备金的利润,它等于税前…...
网络编程作业day7
作业项目:基于UDP的聊天室 服务器代码: #include <myhead.h>//定义客户信息结构体 typedef struct magtye {char type; //消息类型char name[100]; //客户姓名char text[1024]; //客户发送聊天信息 }msg_t;//定义结构体存储…...

【Vision Pro杀手级应用】3D音乐会/演唱会,非VR视频播放的形式,而是实实在在的明星“全息”形象,在你的面前表演
核心内容形式:体积视频 参考对标案例深度解读: 体积视频,这一全新的内容形式,正在引领我们进入一个前所未有的四维体验时代。它将传统的演艺形式推向了新的高度,让我们能够更加深入地沉浸在虚拟世界中,感受前所未有的视听盛宴。 在这一领域,有一个引人注目的案例,那…...

变频器学习
西门子变频器 SINAMICS V20 入门级变频器 SINAMICS G120C...
Linux Ubuntu系统安装MySQL并实现公网连接本地数据库【内网穿透】
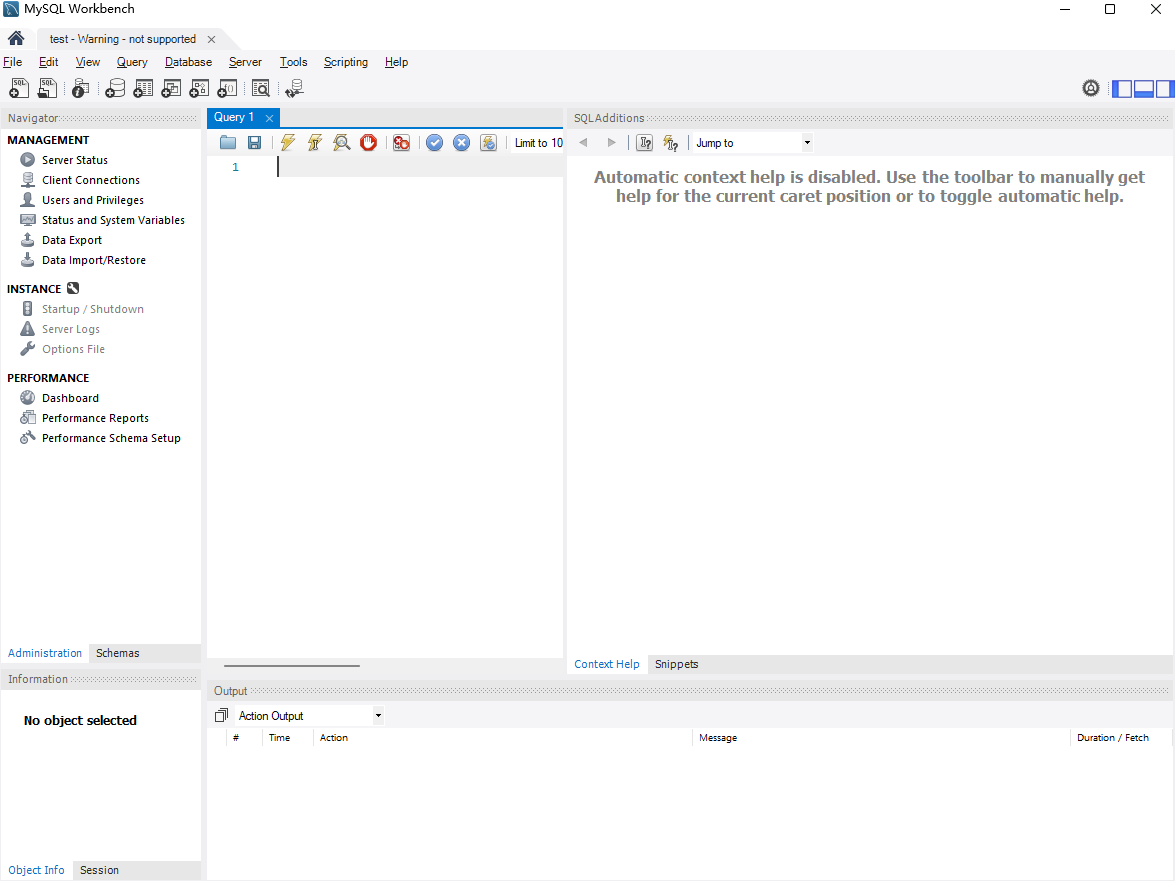
文章目录 前言1 .安装Docker2. 使用Docker拉取MySQL镜像3. 创建并启动MySQL容器4. 本地连接测试4.1 安装MySQL图形化界面工具4.2 使用MySQL Workbench连接测试 5. 公网远程访问本地MySQL5.1 内网穿透工具安装5.2 创建远程连接公网地址5.3 使用固定TCP地址远程访问 前言 本文主…...

0048__Unix传奇
Unix传奇 (上篇)_unix传奇(上篇)-CSDN博客 Unix传奇 (下篇)-CSDN博客 Unix现状与未来——CSDN对我的采访_nuix邮件系统行业地位-CSDN博客...

蓝桥杯-排序
数组排序 Arrays.sort(int[] a) 这种形式是对一个数组的所有元素进行排序,并且时按从小到大的顺序。 package Work;import java.util.*;public class Imcomplete {public static void main(String args[]) {int arr[]new int [] {1,324,4,5,7,2};Arrays.sort(arr)…...
计算机设计大赛 深度学习的视频多目标跟踪实现
文章目录 1 前言2 先上成果3 多目标跟踪的两种方法3.1 方法13.2 方法2 4 Tracking By Detecting的跟踪过程4.1 存在的问题4.2 基于轨迹预测的跟踪方式 5 训练代码6 最后 1 前言 🔥 优质竞赛项目系列,今天要分享的是 基于深度学习的视频多目标跟踪实现 …...

高性能JSON框架之FastJson的简单使用
高性能JSON框架之FastJson的简单使用、 1.前言 1.1.FastJson的介绍: JSON协议使用方便,越来越流行,JSON的处理器有很多,这里我介绍一下FastJson,FastJson是阿里的开源框架,被不少企业使用,是一个极其优秀的Json框架,Github地址: FastJson 1.2.FastJson的特点: 1.F…...
)
★判断素数的几种方法(由易到难,由慢到快)
素数的定义: 素数,又称为质数,指的是“大于1的整数中,只能被1和这个数本身整除的数”。换句话说,素数是只有两个正约数(1和本身)的自然数。素数在数论中有着重要的地位,且素数的个数…...

vue svelte solid 虚拟滚动性能对比
前言 由于svelte solid 两大无虚拟DOM框架,由于其性能好,在前端越来越有影响力。 因此本次想要验证,这三个框架关于实现表格虚拟滚动的性能。 比较版本 vue3.4.21svelte4.2.12solid-js1.8.15 比较代码 这里使用了我的 stk-table-vue(np…...
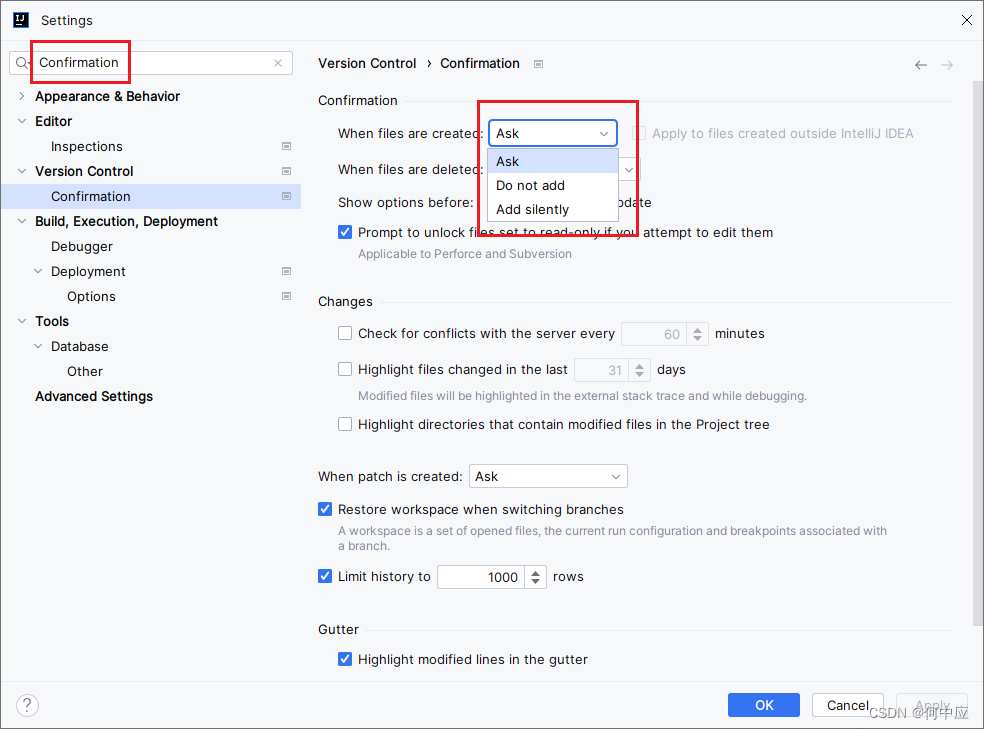
IDEA中新增文件,弹出框提示是否添加到Git点错了,怎么重新设置?
打开一个配置了Git的项目,新增一个文件,会弹出下面这个框。提示是否将新增的文件交给Git管理。 一般来说,会选择ADD,并勾选Dont ask agin,添加并不再询问。如果不小心点错了,可在IDEA中重新设置(…...

LV15 day5 字符设备驱动读写操作实现
一、读操作实现 ssize_t xxx_read(struct file *filp, char __user *pbuf, size_t count, loff_t *ppos); 完成功能:读取设备产生的数据 参数: filp:指向open产生的struct file类型的对象,表示本次read对应的那次open pbuf&#…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...
