★判断素数的几种方法(由易到难,由慢到快)
素数的定义:
素数,又称为质数,指的是“大于1的整数中,只能被1和这个数本身整除的数”。换句话说,素数是只有两个正约数(1和本身)的自然数。素数在数论中有着重要的地位,且素数的个数是无限的。例如,2、3、5、7、11、13等都是素数。判断一个数是否为素数的方法有多种,包括试除法、埃筛法等。
暴力法:
素数判定,是检验一个给定的整数是否为素数的测试。
判断 n 是否为素数时,最简单的方式就是暴力法:遍历的所有大于 1 且小于 n 的整数,判断 n 是否可以被这些数整除,如果不存在可以整除的数,则为素数;否则为合数。
#include <bits/stdc++.h>
using namespace std;//暴力法bool isPrime(int n) { if (n <= 1) return false; for (int i = 2; i <= n-1; i++) { if (n % i == 0) { return false; } } return true;
} int main() { int n; cout << "Enter a number: "; cin >> n; if (isPrime(n)) std::cout << n << " is a prime number." << std::endl; else std::cout << n << " is not a prime number." << std::endl; return 0;
}
暴力法的优化:
暴力法效率极低,如果n为一万,则核心代码要跑n-2次,其实我们只需要判断2~√n个数,因为一个数如果可以因数分解(不是质数),那么分解得到的两个数一定是一个小于等于√n,一个大于等于√n,一个合数一定由两个自然数相乘,一个大于等于平方根一个小于等于平方根,并且成对存在,所以只判断前根号个。这时我们需要使用sqrt函数来求根号。
代码如下:
#include <bits/stdc++.h>
using namespace std;//暴力法的优化
bool isPrime(int n) { if (n <= 1) return false; for (int i = 2; i <= sqrt(n); i++) { if (n % i == 0) { return false; } } return true;
} int main() { int n; cout << "Enter a number: "; cin >> n; if (isPrime(n)) std::cout << n << " is a prime number." << std::endl; else std::cout << n << " is not a prime number." << std::endl; return 0;
}
埃式筛选:
埃拉托斯特尼筛法(Sieve of Eratosthenes)是一种简单且古老的用来找出一定范围内所有素数的算法。其基本思想是从2开始,将每个素数的各个倍数,标记为合数(非素数),直到标记到所给定的范围为止。
具体的步骤如下
-
创建一个布尔数组
notPrime[0..n+1],并初始化为true。这个数组用来表示对应索引的数是否为素数(true表示可能是素数,false表示不是素数或还未检测)。通常notPrime[0]和notPrime[1]会被设为false,因为0和1不是素数。 -
从
p = 2开始,即最小的素数,一直到sqrt(n)(n为要筛的范围)。 -
如果
notPrime[p]为true,则p是一个素数。 -
接下来,标记
p的所有倍数(从p*p开始,一直到n)为非素数。即设置notPrime[p*i]为false,其中i从p开始递增。 -
重复步骤3和4,直到
p超出sqrt(n)。 -
最后,数组中剩余标记为
true的索引对应的数就是素数。
#include <bits/stdc++.h>
using namespace std;//埃式筛法
bool sieveOfEratosthenes(int n,vector<bool>& notPrime) { for (int p = 2; p * p <= n; p++) { //将素数的倍数全部标记为false if (notPrime[p] == true) { for (int i = p * p; i <= n; i += p) notPrime[i] = false; } } return notPrime[n];
}
int main() { int n; cout << "Enter a number: "; cin >> n; vector<bool> notPrime(n + 1, true);notPrime[0] = notPrime[1] = false; if(sieveOfEratosthenes(n,notPrime)) cout << n << " is a prime number." << std::endl; else cout << n << " is not a prime number." << std::endl;return 0;
}欧拉筛选:
具体的步骤如下
埃式筛选任然有一些可以改进的地方,比如说当筛选到2时,会将4,、6、8、10、12等2的倍数标记为false。然而当筛选到3时,会将6、9、12、15等3的倍数标记为fasle,这其中6和12等既是2的倍数又是3的倍数的一些数,会被重复标记。
欧拉筛选素数法是一种更加高效的素数筛选算法,它的基本思想是从2开始,将每个素数的倍数都标记成合数,但与传统的埃拉托斯特尼筛法(Sieve of Eratosthenes)不同,欧拉筛选保证了每个合数只被其最小质因子筛选一次,从而实现了线性的时间复杂度。
下面是欧拉筛选素数法的详细实现步骤:
-
初始化:创建一个布尔数组
isPrime[0..n],并全部初始化为true。这个数组用于表示从0到n的每个数是否为素数。通常,我们会忽略0和1,因为它们不是素数。 -
筛选过程:
- 从
p = 2开始,这是第一个素数。 - 对于每个
p,遍历所有i(从p的平方开始,直到n),并将isPrime[i*p]设置为false,因为i*p显然不是素数(除非i是1,但这在循环开始条件中已经被排除了)。 - 在遍历
i的过程中,如果发现isPrime[i]已经为false,则跳出内层循环。这是因为如果i不是素数,那么i*p已经被一个比p更小的素数标记过了,无需再次标记。 - 继续增加
p,直到所有小于等于n的数都被检查。
- 从
-
收集素数:最后,遍历
isPrime数组,所有标记为true的位置对应的数就是素数。
这个算法的关键在于,它确保了每个合数只被其最小的质因子筛选一次。这是通过在内层循环中检查 isPrime[i] 并在发现其为 false 时跳出循环来实现的。这样,每个合数只会在其最小质因子第一次出现时被标记,从而避免了重复标记,提高了效率。
欧拉筛选素数法的时间复杂度是线性的,即 O(n),这使得它在处理大规模数据时比传统的埃拉托斯特尼筛法更加高效。
需要注意的是,虽然欧拉筛选素数法在某些情况下比埃拉托斯特尼筛法更优,但它并不是在所有情况下都是最佳选择。具体使用哪种算法取决于问题的具体要求和数据的规模。
#include <bits/stdc++.h>
using namespace std;
vector<int> primes;
void linearSieve(int n) { vector<bool> isPrime(n + 1, true); for (int i = 2; i <= n; ++i) { if (isPrime[i]) { primes.push_back(i); } for (size_t j = 0; j < primes.size() && i * primes[j] <= n; ++j) { isPrime[i * primes[j]] = false; if (i % primes[j] == 0) { break; } } } } int main() { int n = 100; // 可以根据需要修改这个值 cout << "Prime numbers up to " << n << " are: "; linearSieve(n); for (int prime : primes) { cout << prime << " "; } return 0;
}对于小范围的素数判断,试除法通常足够高效;对于需要生成大量素数的情况,埃筛法更为合适;
相关文章:
)
★判断素数的几种方法(由易到难,由慢到快)
素数的定义: 素数,又称为质数,指的是“大于1的整数中,只能被1和这个数本身整除的数”。换句话说,素数是只有两个正约数(1和本身)的自然数。素数在数论中有着重要的地位,且素数的个数…...

vue svelte solid 虚拟滚动性能对比
前言 由于svelte solid 两大无虚拟DOM框架,由于其性能好,在前端越来越有影响力。 因此本次想要验证,这三个框架关于实现表格虚拟滚动的性能。 比较版本 vue3.4.21svelte4.2.12solid-js1.8.15 比较代码 这里使用了我的 stk-table-vue(np…...
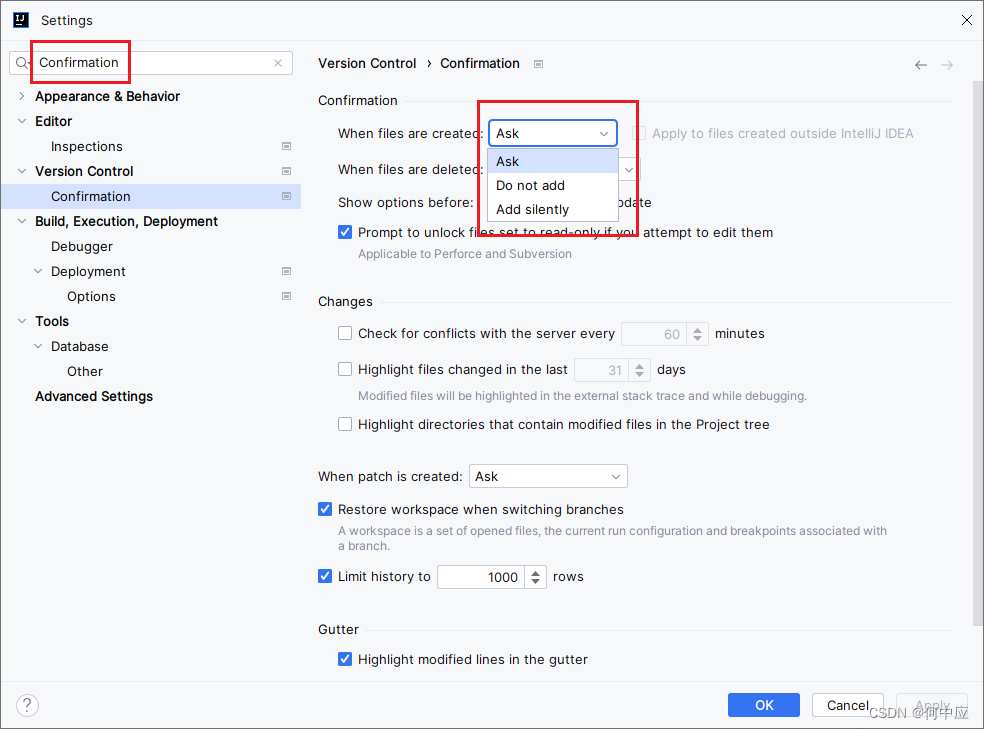
IDEA中新增文件,弹出框提示是否添加到Git点错了,怎么重新设置?
打开一个配置了Git的项目,新增一个文件,会弹出下面这个框。提示是否将新增的文件交给Git管理。 一般来说,会选择ADD,并勾选Dont ask agin,添加并不再询问。如果不小心点错了,可在IDEA中重新设置(…...

LV15 day5 字符设备驱动读写操作实现
一、读操作实现 ssize_t xxx_read(struct file *filp, char __user *pbuf, size_t count, loff_t *ppos); 完成功能:读取设备产生的数据 参数: filp:指向open产生的struct file类型的对象,表示本次read对应的那次open pbuf&#…...

Uninty 鼠标点击(摄像机发出射线-检测位置)
平面来触发碰撞,胶囊用红色材质方便观察。 脚本挂载到胶囊上方便操作。 目前实现的功能,鼠标左键点击,胶囊就移动到那个位置上。 using System.Collections; using System.Collections.Generic; using UnityEngine;public class c6 : MonoBe…...

描述下Vue自定义指令
描述下Vue自定义指令 (1)自定义指令基本内容(2)使用场景(3)使用案例 在 Vue2.0 中,代码复用和抽象的主要形式是组件。然而,有的情况下,你仍然需要对普通 DOM 元素进行底层…...

2024.3.7
作业: 1、OSI的七层网络模型有哪些,每一层有什么作用? (1)应用层 负责处理不同应用程序之间的通信,需要满足提供的协议,确保数据发送方和接收方的正确 (2)表示层…...

this.$watch 侦听器 和 停止侦听器
使用组件实例的$watch()方法来命令式地创建一个侦听器; 它还允许你提前停止该侦听器 语法:this.$watch(data, method, object) 1. data:侦听的数据源,类型为String 2. method:回调函数&#x…...

P1030 [NOIP2001 普及组] 求先序排列题解
题目 给出一棵二叉树的中序与后序排列。求出它的先序排列。(约定树结点用不同的大写字母表示,且二叉树的节点个数≤8)。 输入输出格式 输入格式 共两行,均为大写字母组成的字符串,表示一棵二叉树的中序与后序排列。…...

【分布式】NCCL Split Tree kernel内实现情况 - 06
相关系列 【分布式】NCCL部署与测试 - 01 【分布式】入门级NCCL多机并行实践 - 02 【分布式】小白看Ring算法 - 03 【分布式】大模型分布式训练入门与实践 - 04 目录 相关系列概述1.1 Tree1.2 double binary tree初始化和拓扑2.1 Tree的初始化与差异2.2 ncclGetBtreeKernel内部…...
)
C语言深入学习 --- 4.自定义类型(结构体+枚举+联合)
第四章 自定义类型:结构体,枚举,联合 结构体 结构体类型的声明 结构的自引用 结构体变量的定义和初始化 结构体的内存对齐 结构体实现位段(位段的填充 和 可移植性) 枚举 枚举类型的定义 枚举的优点 枚举的使…...

AI自然语言中默认上下文长度4K 几K是什么意思?
环境: 4K 问题描述: AI自然语言中默认上下文长度4K 几K是什么意思? 解决方案: 在自然语言处理中,“k” 表示 “千”,是一种简写方式。当我们说 “4k” 时,实际上指的是 “4,000”。在上下文…...

vSphere 8考试认证题库 2024最新(VCP 8.0版本)
VMware VCP-DCV(2V0-21.23)认证考试题库,已全部更新,答案已经完成校对,完整题库请扫描上方二维码访问。正常考可以考到450分以上(满分500分,300分通过) An administrator is tasked …...

系统学习Python——装饰器:“私有“和“公有“属性案例-[装饰器参数、状态保持和外层作用域]
分类目录:《系统学习Python》总目录 文章《系统学习Python——装饰器:“私有“和“公有“属性案例-[实现私有属性]》中使用的类装饰器接受任意多个参数来命名私有属性。然而真正发生的情况是,参数传递给了Private函数,然后Private…...

星辰天合参与编制 国内首个可兼顾 AI 大模型训练的高性能计算存储标准正式发布
近日,在中国电子工业标准化技术协会高标委的支持和指导下,XSKY星辰天合作为核心成员参与编制的《高性能计算分布式存储系统技术要求》团体标准,在中国电子工业标准化技术协会网站正式发布。 该团体标准强调了分布式存储系统对包括传统高性能计…...

算法训练day38动态规划基础Leetcode509斐波纳切数70爬楼梯746使用最小花费爬楼梯
什么是动态规划 对于动态规划问题,我将拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了! 确定dp数组(dp table)以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数组&a…...
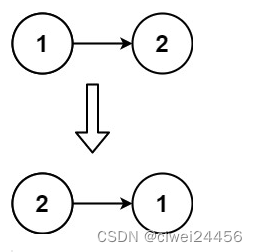
Leetcode 206. 反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 示例 1: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1] 示例 2: 输入:head [1,2] 输出:[2,1] 示例 3: 输…...

电子科技大学课程《计算机网络系统》(持续更新)
前言 本校的课程课时有所缩减,因此可能出现与你学习的课程有所减少的情况,因此对其他学校的同学更多的作为参考作用。本文章适合学生的期中期末考试,以及想要考研电子科技大学的同学,电子科技大学同学请先看附言。 第一章 计算…...

HBase介绍、特点、应用场景、生态圈
目录: 一、HBase简介 二、NoSQL和关系型数据库对比 三、HBase特点 四、应用场景 五、HBase生态圈技术 一、HBase简介 HBase是一个领先的NoSQL数据库 是一个面向列存储的NoSQL数据库 是一个分布式Hash Map,底层数据是Key-Value格式 基于Coogle Big Table论文 使用HD…...

蓝桥杯错误记录
今天在做 小蜜蜂的综合案例的时候,数码管显示,有重影。 #include <STC15F2K60S2.H> unsigned char num; unsigned char code Duan[22]{0xc0,0xf9,0xa4,0xb0,0x99,0x92,0x82,0xf8,0x80,0x90,0x88,0x80, 0xc6,0xc0,0x86,0x8e,0xbf,0x7f,0XC1,0X8C,0…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
