GCN 翻译 - 2
2 FAST APROXIMATE CONVOLUTIONS ON GRAPHS
在这一章节,我们为这种特殊的的图基础的神经网络模型f(X, A)提供理论上的支持。我们考虑一个多层的图卷积网络(GCN),它通过以下方式进行层间的传播:
这里,是无向图邻接矩阵加上自己本身。
是对称矩阵,
,
是层的训练权重矩阵。
表示激活函数,例如ReLu.
是
层的激活矩阵,
.在接下来中,我们将会展示,这种规则的传播方式是局部谱域滤波的一阶近似。
2.1 SPECTRAL GRAPH CONVOLUTIONS
我们考虑图上的谱域卷积 : 多维信号,用参数
定义的傅里叶过滤器
,i.e.:
这里U是归一化的图拉普拉斯矩阵的特征向量矩阵,这里,
对角矩阵是特征值,
是x的图傅里叶的转换。我们可以理解
是拉普拉斯矩阵L的特征值的函数,即
。计算公式(3)是非常繁重的计算,因为特征向量的矩阵U的乘法是
。并且,在大的图上计算L的特征值分解,其计算量之大以至于无法做到。为了规避在大图上特征值分解的问题,
近似是切比雪夫多项式
级截断
:
。
表示L的最大特征值。
是切比雪夫向量的系数。切比雪夫多项式递归地定义为
,这里面
。
回到我们信号x过滤器
这里;可以轻易验证
。这个表达式是K阶截断的拉普拉斯多项式近似,它依赖于中心节点周围做多K个节点的作用。公式 5的复杂度是
,随着边的数量线性增长。Defferrard et al 使用K阶卷积定义了图上的卷积网络。
2.2 LAYER-WISE LINEAR MODEL
通过公式5,图卷积神经网络可以叠多个卷积层,每一层都是非线性的。现在,如果我们将层的卷积操作K=1,即图谱域拉普拉斯矩阵L的限行函数。
这种一阶的线性方式,我们仍然可以罗列多层的卷积层,这不局限于切比雪夫多项式。我直觉期望这样的模型能够对于点的度数很高的分布(例如,社交网络、引用网络、知识图谱和其他一些真实世界的数据库)的图结构起到减轻过拟合的作用。并且,对于一定的计算资源,这种一阶的layer-wise方式能够建立更深的网络。
这样一种GCN的方式,我们近似,训练过程中,网络的参数适应如下方式:
这里2个自由参数和
。这个过滤器的参数被整个网络共享。多层卷积过滤能够卷积到一个节点的第
层邻居,k就是图神经网络卷积层的层数。
在实际中,限制参数的数量以减少计算(例如矩阵乘法)已解决过拟合的问题,这种优化可以得到如下公式
一个参数。注意
的特征值取值范围在
。在神经网络里面叠多层这样的操作将导致数值不稳定,以及神经网络梯度的消失。为了有效缓解这个问题,我们将使用再归一化的技巧:
,
和
。
我们可以将上述的定义真正泛化到一个信号,带有C个输入通道(例如,每一个节点有C维的特征向量),F过滤和特征映射如下:
这里是过滤矩阵的参数,
是卷积信号矩阵。这个过滤操作有
的复杂度,
是稀疏矩阵和稠密矩阵的乘积。
相关文章:
GCN 翻译 - 2
2 FAST APROXIMATE CONVOLUTIONS ON GRAPHS 在这一章节,我们为这种特殊的的图基础的神经网络模型f(X, A)提供理论上的支持。我们考虑一个多层的图卷积网络(GCN),它通过以下方式进行层间的传播: 这里,是无…...
HBase 的安装与部署
目录 1 启动 zookeeper2 启动 Hadoop3 HBase 的安装与部署4 HBase 高可用 1 启动 zookeeper [huweihadoop101 ~]$ bin/zk_cluster.sh start2 启动 Hadoop [huweihadoop101 ~]$ bin/hdp_cluster.sh start3 HBase 的安装与部署 (1)将 hbase-2.0.5-bin.tar.…...

236.二叉搜索树的公共祖先
236.二叉树的公共祖先 思路 看到题想的是找到两个点的各自路径利用stack保存,根据路径长度大小将两个stack的值对齐到同一层,之后同时出栈节点,若相同则找到祖先节点。但是效率不高 看了大佬代码,递归思想很难理解。 根据大佬…...
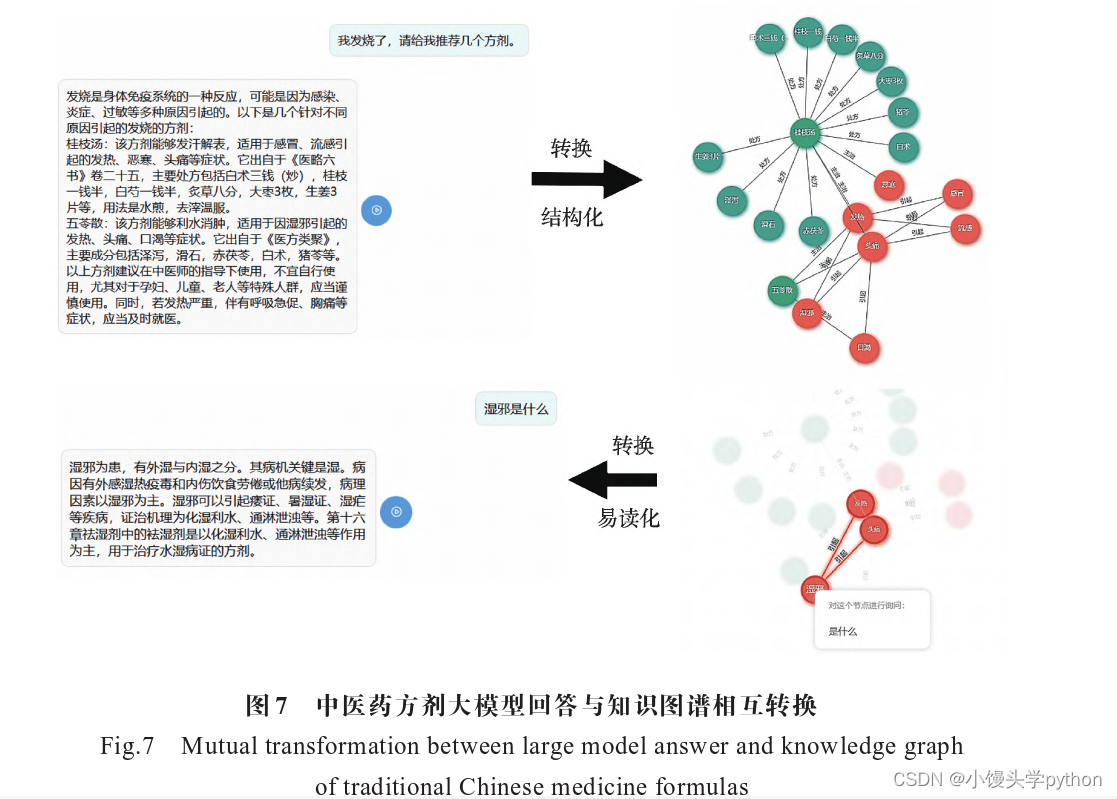
【论文精读】大语言模型融合知识图谱的问答系统研究
💗💗💗欢迎来到我的博客,你将找到有关如何使用技术解决问题的文章,也会找到某个技术的学习路线。无论你是何种职业,我都希望我的博客对你有所帮助。最后不要忘记订阅我的博客以获取最新文章,也欢…...
LabVIEW高精度天线自动测试系统
LabVIEW高精度天线自动测试系统 系统是一个集成了LabVIEW软件的自动化天线测试平台,提高天线性能测试的精度与效率。系统通过远程控制测试仪表,实现了数据采集、方向图绘制、参数计算等功能,特别适用于对天线辐射特性的精确测量。 在天线的…...
7.3 支付模块 - 创建订单、查询订单、通知
支付模块 - 创建订单、查询订单、通知 文章目录 支付模块 - 创建订单、查询订单、通知一、生成支付二维码1.1 数据模型1.1.1 订单表1.1.2 订单明细表1.1.3 支付交易记录表 1.2 执行流程1.3 Dto1.3.1 AddOrderDto 商品订单1.3.2 PayRecordDto支付交易记录扩展字段1.3.3 雪花算法…...

灵魂指针,教给(一)
欢迎来到白刘的领域 Miracle_86.-CSDN博客 系列专栏 C语言知识 先赞后看,已成习惯 创作不易,多多支持! 一、内存和地址 1.1 内存 在介绍知识之前,先来想一个生活中的小栗子: 假如把你放在一个有100间屋子的酒店…...
Linux 开发工具 yum、git、gdb
目录 一、yum 1、软件包 2、rzsz 3、注意事项 4、查看软件包 5、安装软件 6、卸载软件 二、git操作 1、克隆三板斧 2、第一次使用会出现以下情况: 未配置用户名和邮箱: push后弹出提示 三、gdb使用 1、背景 2、使用方法 例一:…...

Markdown
这里写自定义目录标题 欢迎使用Markdown编辑器 新的改变 功能快捷键 合理的创建标题,有助于目录的生成 如何改变文本的样式 插入链接与图片 如何插入一段漂亮的代码片 生成一个适合你的列表 创建一个表格 设定内容居中、居左、居右 SmartyPants 创建一个自定义列表 …...

【Oracle】oracle中sql给表新增字段并添加注释说明;mysql新增、修改字段
oracle中sql给表新增字段并添加注释说明 ALTER TABLE 表名 ADD 字段名 类型 COMMENT ON COLUMN 表面.字段名 IS ‘注释内容’ ALTER TABLE GROUP ADD T NUMBER(18) COMMENT ON COLUMN GROUP.T IS ‘ID’ mysql新增、修改字段、已有字段增加默认值 ALTER TABLE 表名 ADD COL…...

【汇总】pytest简易教程
pytest作为python技术栈里面主流、火热的技术,非常有必要好好学一下,因为工作和面试都能用上; 它不仅简单易用,还很强大灵活,重点掌握fixture、parametrize参数化、allure-pytest插件等,这些在后续自动化框…...

openssl调试记录
openssl不能直接解密16进制密文,需要把密文转化成base64格式才能解密 调试记录如下:...

3.7练习题解
一共五道题: 1. PERKET: 观察容易发现n的值很小,所以我们可以考虑使用dfs的方法进行解答,首先我们可以考虑一共有n种配料,那么我们就可以考虑到可以选择1到n种配料数目,然后基于这个思路我们再对其进行判断…...

MQ的消费模式-消息是推还是拉
文章目录 概述RocketMQ默认pushRabbitMQ默认pushKafka默认拉PullActiveMQ默认push 概述 MQ的消费模式可以大致分为两种,一种是推Push,一种是拉Pull Push是服务端主动推送消息给客户端,Pull是客户端需要主动到服务端轮询获取数据。 推优点是及…...
一个平台满足你对测试工具的所有需求
背景 目前,测试人员普遍使用的测试工具有Postman、JMeter等,但这些工具都存在一定的局限性。例如,Postman缺少对API性能测试方面的支持,而JMeter则缺乏一个整合测试报告、测试脚本的统一管理系统以及UI测试功能。 RunnerGo是什么…...

【C语言】【字符串函数】【超详解】【上】!!!
前言: 在学习C语言的过程中,字符串、字符数组等对新手来说总是会有疏忽,在已有的库函数中,我们平时用到最多的就是关于字符串的函数,今天我们就来详细学习字符串函数的相关内容。 下面我们就开始讲解字符串函数&#x…...

算法沉淀——动态规划之其它背包问题与卡特兰数(leetcode真题剖析)
算法沉淀——动态规划之其它背包问题与卡特兰数 二维费用的背包问题01.一和零02.盈利计划 似包非包组合总和 Ⅳ 卡特兰数不同的二叉搜索树 二维费用的背包问题 01.一和零 题目链接:https://leetcode.cn/problems/ones-and-zeroes/ 给你一个二进制字符串数组 strs…...

selenium中ChromeDriver配置,一把过,并且教你伪装
最近正值毕业季,我之前不是写了个问卷星代码嘛,昨晚上有人凌晨1点加我,问我相关内容。 由于我之前C盘重装了一下,导致我很多东西空有其表,实际不能用,借此机会,向大家编写ChromeDriver配置&…...
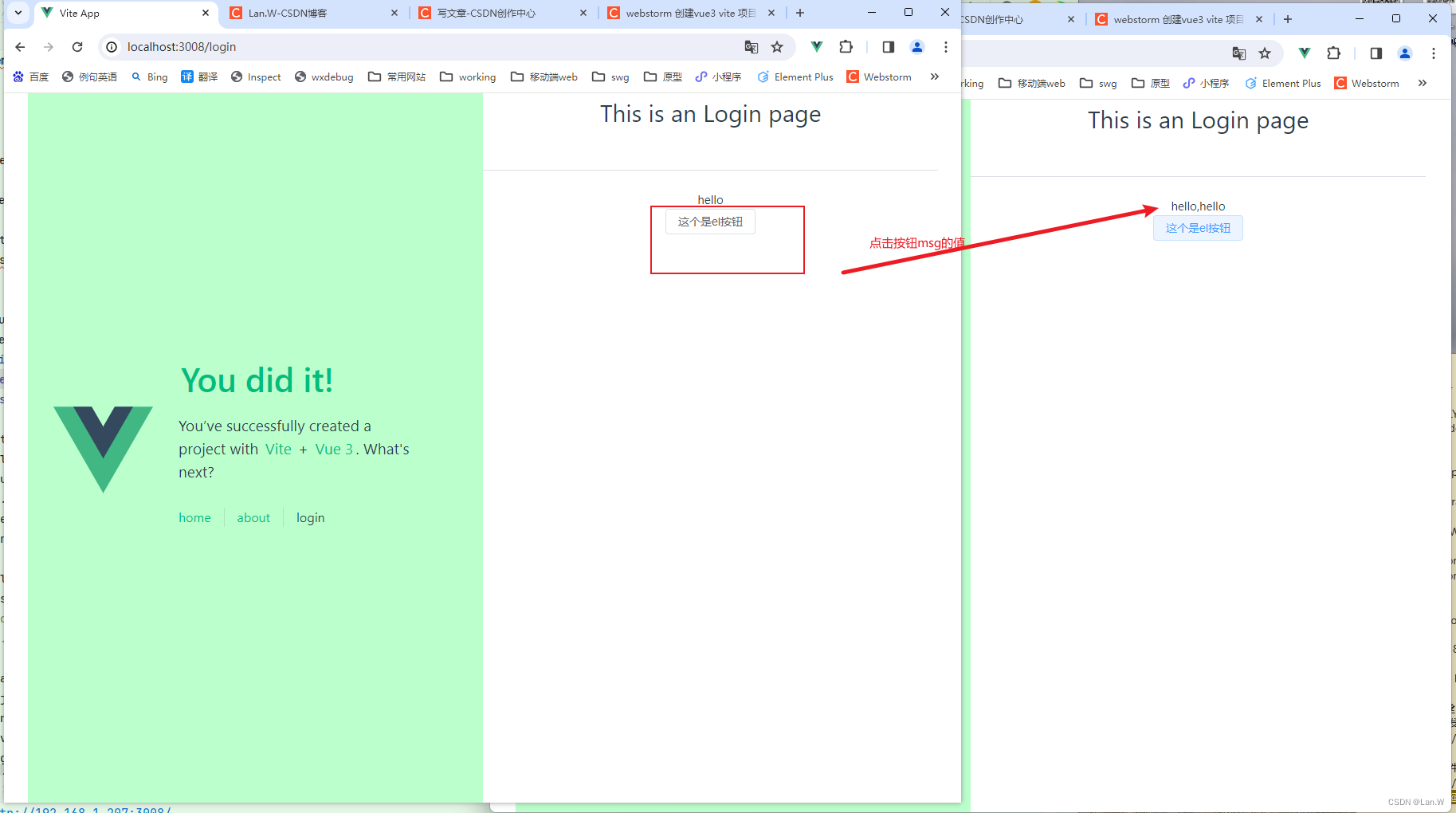
vue3 + vite 项目可以使用纯Js开发吗?
答案:可以 创建项目: 按照链接参考或者按官方: webstorm 创建vue3 vite 项目-CSDN博客 项目目录 tsconfig.json 配置允许js allowJs指定是否编译js文件,在任意文件当中,如果我们模块使用js写的,那么我们需要 将all…...
Java EE之线程安全问题
一.啥是线程安全问题 有些代码,在单个线程执行时完全正确,但同样的代码让多个线程同时执行,就会出现bug。例如以下代码: 给定一个变量count,让线程t1 t2分别自增5000次,然后进行打印,按理说co…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...
