蓝桥杯真题(解码)小白入!
本来看这个题感觉很简单,不就是Ascall值换来换去嘛,其实也真的这样,但是对于小白来说,ascall根本记不住
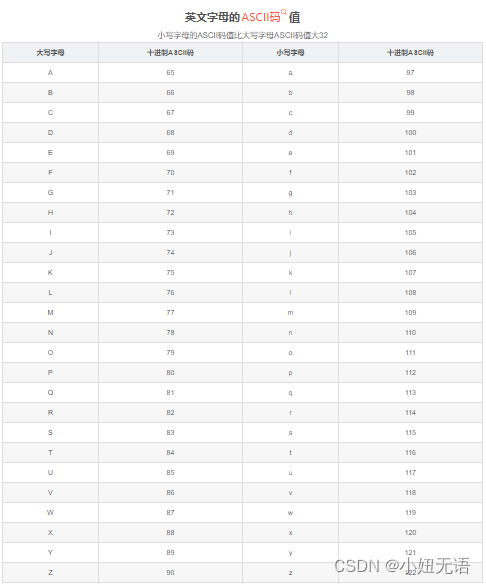
题目说了,每个数不会重复超过9次(这见到那多了,不然根本不会写)
其次如何实现字符英文和整型之间转换和字符数字与整形之间的转换,又是个点
首先说说,字符英语和整型的转换
int temp='a';
这样就OK了,当你输出temp,就是对应a的Ascall值
然后就是,字符数字与整形之间的转换
第一步也是
int temp='3';//你要知道这里转化过来的是3的Ascall值,不是数字3
这时,就有同学疑问,呢要怎么变回3
其实Ascall很有规律的,数字的Ascall是连续的
'0'的Ascall值为48,'3'是51
所以两者相减就行
int temp='3'-'0';
这样就ok了
好了,回到题上,看完上面应该就明了,直接上代码
#include<bits/stdc++.h>
#include<cstring>
using namespace std;char a[110],b;
int temp;
int main()
{cin.tie(0);cout.tie(0);//就是输入输出加个速cin>>a;int h=strlen(a);for(int i=0;i<h;i++){int f=(int)a[i]; //先转化每个字符的Ascallif(f>=65&&f<=90||f>=97&&f<=122)//通过Ascall可看出大写A-Z范围是65-90,小写a-z范围是97-122{b=a[i];temp=1;//这里统一了,就算是要重复的字母也会跟不重复的字母同时输出一次}else {temp=a[i]-'0';temp--;//因为它在上一步就输出过一次了}while(temp--)cout<<b;}return 0;
}相关文章:

蓝桥杯真题(解码)小白入!
本来看这个题感觉很简单,不就是Ascall值换来换去嘛,其实也真的这样,但是对于小白来说,ascall根本记不住 题目说了,每个数不会重复超过9次(这见到那多了,不然根本不会写) 其次如何实现…...

并发包中的ConcurrentLinkedQueue和LinkedBlockingQueue有什么区别?
第20讲 | 并发包中的ConcurrentLinkedQueue和LinkedBlockingQueue有什么区别? 在上一讲中,我分析了 Java 并发包中的部分内容,今天我来介绍一下线程安全队列。Java 标准库提供了非常多的线程安全队列,很容易混淆。 今天我要问你的…...
分享四个前端Web3D动画库在Threejs中使用的动画库以及优缺点附地址
Threejs中可以使用以下几种动画库:Tween.js:Tween.js是一个简单的缓动库,可以用于在three.js中创建简单的动画效果。它可以控制数值、颜色、矢量等数据类型,并提供了多种缓动函数,例如线性、弹簧、强化、缓冲等等。区别…...

谷歌浏览器和火狐浏览器永久禁用缓存【一劳永逸的解决方式】
目录 前言 谷歌浏览器 方式一 方式二 火狐浏览器 前言 缓存对于开发人员来说异常的痛苦,很多莫名其妙的bug就是由缓存导致的,但当我们在网上查找禁用缓存的方式时,找到的方式大多数都是在开发者工具的面板中勾选禁用缓存的选项,但这种方式有个弊端就是需要一直打开这个…...

kibana查看日志
一、背景 kibana收集日志功能很强大,之前只是简单的使用,此次系统学习了解并分享一波 二、kibana查看日志的基本使用 1.选择查询的服务和日志文件 注意:每个应用配置了开发与生产环境,需要找到指定的应用 1.1选择对应的应用 1.…...
JS 异步接口调用介绍
JS 异步接口调用介绍 Js 单线程模型 JavaScript 语言的一大特点就是单线程,也就是说,同一个时间只能做一件事。这样设计的方案主要源于其语言特性,因为 JavaScript 是浏览器脚本语言,它可以操纵 DOM ,可以渲染动画&a…...
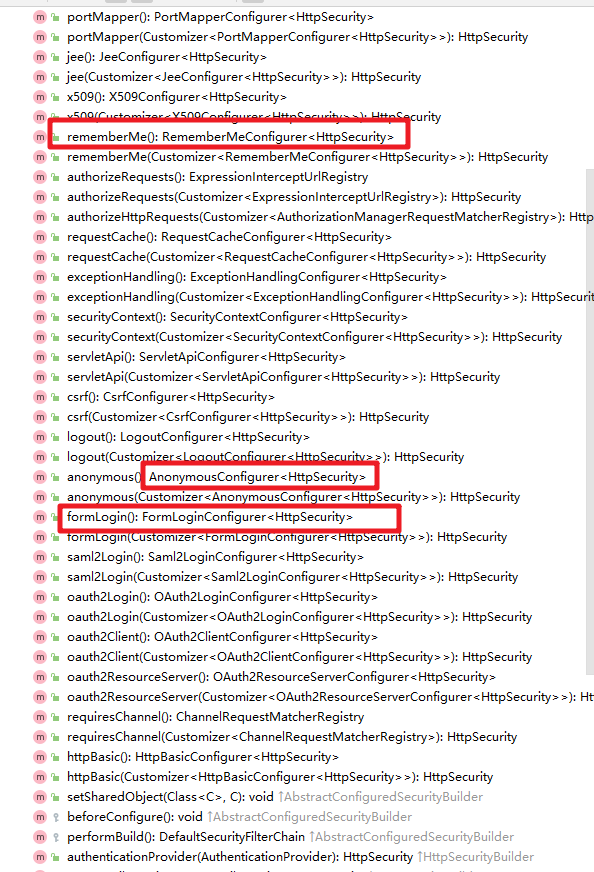
5.深入理解HttpSecurity的设计
深入理解HttpSecurity的设计 一、HttpSecurity的应用 在前章节的介绍中我们讲解了基于配置文件的使用方式,也就是如下的使用。 也就是在配置文件中通过 security:http 等标签来定义了认证需要的相关信息,但是在SpringBoot项目中,我们慢慢脱离…...
)
opencv-python numpy常见的api接口汇总(持续更新)
前言 最近写代码总是提笔忘api,因为图像处理代码写的比较多,所以想着把一些常用的opencv的api,包括numpy的api做一个记录,后面再忘记的时候,就不用去google挨个搜索了,只需要在自己的博客中一查就全知道了…...
)
概率论小课堂:伯努利实验(正确理解随机性,理解现实概率和理想概率的偏差)
文章目录 引言I 伯努利试验1.1 伯努利分布(二项式分布)1.2 数学期望值(简称期望值)1.3 平方差(简称方差)1.4 标准差1.5 小结引言 假设买彩票中奖的概率是一百万分之一,如果要想确保成功一次,要买260万次彩票。你即使中一回大奖,花的钱要远比获得的多得多。 很多人喜…...
加密功能实现
文章目录1. 前言2. 密码加密1. 前言 本文 主要实现 对密码进行加密 ,因为 使用 md5 容易被穷举 (彩虹表) 而破解 ,使用 spring security 框架又太大了 (杀鸡用牛刀) 。 所以本文 就自己实现一个密码加密 . 2. 密码加密 这里我们通过 加盐是方式 来 对…...
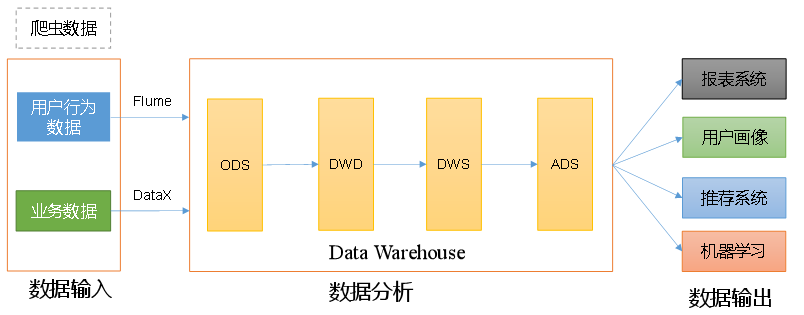
大数据项目实战之数据仓库:用户行为采集平台——第1章 数据仓库概念
第1章 数据仓库概念 数据仓库(Data Warehouse),是为企业制定决策,提供数据支持的。可以帮助企业改进业务流程、提高产品质量等。 数据仓库的输入数据通常包括:业务数据、用户行为数据和爬虫数据等 业务数据…...
在生物制药业应用)
NTP对时服务器(NTP电子时钟)在生物制药业应用
NTP对时服务器(NTP电子时钟)在生物制药业应用 NTP对时服务器(NTP电子时钟)在生物制药业应用 8.1 系统概述 时钟系统为生物制药厂网络控制中心调度员、车场值班员及各部门工作人员提供统一的标准时间信息,也为本工程其它…...

JPA 之 QueryDSL-JPA 使用指南
Querydsl-JPA 框架(推荐) 官网:传送门 参考: JPA整合Querydsl入门篇SpringBoot环境下QueryDSL-JPA的入门及进阶 概述及依赖、插件、生成查询实体 1.Querydsl支持代码自动完成,因为是纯Java API编写查询࿰…...

如何找回回收站删除的视频?这三种方法可以试试
在使用电脑过程中,我们可能会误删重要的文件,特别是影音文件。在这样的情况下,我们可以从计算机的回收站中找回已经被删除的视频。但是有时候,我们可能会不小心清空回收站,这时候就需要一些技巧来恢复回收站删除的视频…...

FPGA_边沿监测理解
一、简易频率计设计中为什么一定要获取下降沿?gate_a:实际闸门信号gate_a_stand:将实际闸门信号打一拍之后的信号gate_a_fall_s:下降沿标志信号cnt_clk_stand: Y值,即在实际闸门信号下,标准时钟信号的周期个数cnt_clk_stand_reg:保存Y值的寄存器核心问题…...

41 42Ping-Pong操作
提高电路吞吐率的结构——Ping-Pong操作 1.Ping-Pong操作原理 作用:为了让两个不匹配的模块进行对接,并且在对接的过程中让这两个模块能够同时工作,提高数据处理的吞吐率(也称throughput效能) 常见的不匹配࿱…...

保护你的数据安全,了解网络安全法!
网络安全法是中国自2017年6月1日起实施的一项法律,旨在保障网络安全和信息安全,维护国家安全和社会稳定。网络安全法覆盖了众多方面,包括网络基础设施安全、网络运营安全、个人信息保护、网络安全监管等,具有重要的法律意义和社会…...
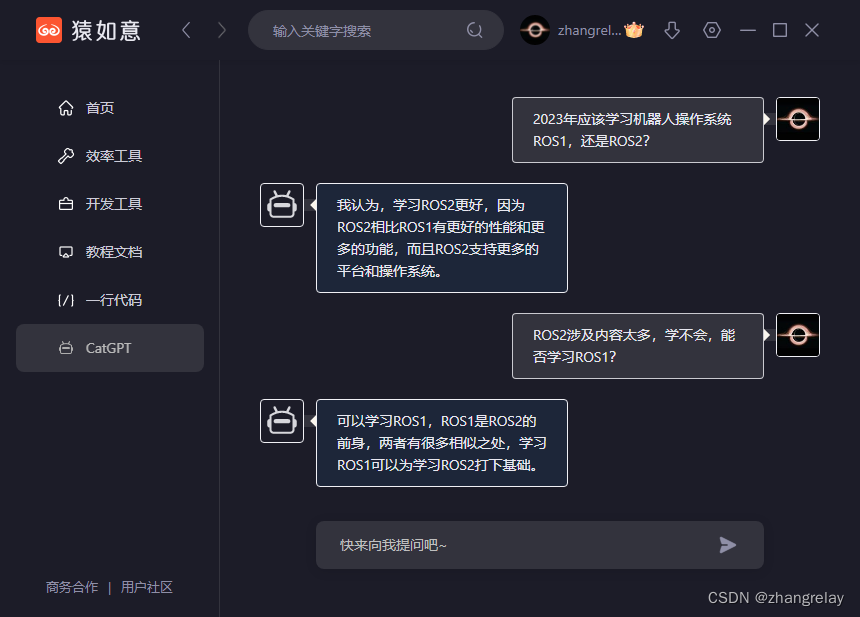
什么是CatGPT-使用效果如何-
个人使用效果,评分优,足以满足教学和填表。程序媛借助CatGPT(ChatGPT更佳),基本上可以秒杀不用此类工具的程序猿(男)!!!问:为什么使用AIGC能大幅度…...

【MySQL】第17章_触发器
第17章_触发器 在实际开发中,我们经常会遇到这样的情况:有 2 个或者多个相互关联的表,如商品信息和库存信息分别存放在 2 个不同的数据表中,我们在添加一条新商品记录的时候,为了保证数据的完整性,必须同时…...

【前端】一个更底层库-React基础知识点第2篇
目录属性状态PROPSPROP VALIDATIONSTATEFORMCONTROLLED COMPONENTSMIXINCOMPONENT APICOMPONENT LIFECYCLETOP API上一篇文章也是React基础知识点,了解到了React是什么?为什么要使用React?还知道了JSX概述,JSX嵌入变量,…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
