洛谷 1025.数的划分
这道题用的知识点是DFS+剪枝。难的不在DFS上,而是在剪枝上如何选择。
思路:这道题我们看到是按照字典序排的,但是,我们注意到,看似是全排列的递归,实则不是。
我们前面也了解过,全排列的数字大小是没有规则的,当然指数型也不可能,这并不涉及到选与不选的问题。而且,我们看到,这些数字有点像升序排列的,所以可能会是组合型递归。但是呢,我们又发现,它们的数字并不是严格单调的,而是有相同的数字在里面排序。这怎么办呢?
改进方法已经在代码里了,就是在进行下一次dfs的时候我们只需要写上i就行,而不是i+1,如果是i+1就会严格单调了。
只是这样写起来,会有数据点TLE。这是为什么呢?因为有些地方是需要剪枝的。那么这里我们怎么剪枝呢?如果你想说在求出来的和不是n的时候剪枝,那也是在全部数字枚举出来的时候才会判断的,仅仅是这样并不能完全剪枝。那该怎么办呢?这里,我们直接在循环里剪枝,也就是在枚举的过程中进行剪枝。怎么剪枝呢?举个例子:
当我们n=7,k=4时,这个时候假如我们已经列举到1,3了,现在正在第三个位置的dfs当中,这个时候按照我们的写法下一个数字肯定是3,最后一个数字也是3,这是对于自己编写的程序的理解。
我们看,如果这几个数字加起来是不是已经超过7了?也就是说,第四个位置我们根本不需要考虑了,前面已经=7了,后面再加就不行了,这里我们直接让循环不去dfs了,而是进行下一次循环。这就省了一次dfs函数的调用!那么,怎么实现这种想法呢?
我们在循环中改进循环条件就行,这和上几次的剪枝是不一样的,这里的剪枝涉及到的是对于在枚举过程中的剪枝,而不是对于全部枚举完之后的剪枝,这里是不同点。在上面的例子中,我们看到,其实知道了第三个数字我们也就知道了第四个数字了。所以,我们只需要循环到第二个位置后,判断后面两个位置的和与前面我们已经计算了的sum相加是不是<=n就行了,这就是优化的地方。
注意:这里的dfs有三个变量,第一个是位置,第二个是从哪个数开始枚举,第三个则是累加的数用来记录的。
#include<iostream>
#include<stdio.h>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<algorithm>
#include<stack>
#include<queue>
#include<sstream>
#include<map>
#include<limits.h>
#include<set>
#define MAX 100010
#define _for(i,a,b) for(int i=a;i<(b);i++)
#define ALL(x) x.begin(),x.end()
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
int arr[MAX];
LL n, m, counts, num;
void dfs(int u,int st,int sum) {if (u > m) {if (sum<n || sum>n)return;else {counts++;}return;}for (int i = st; sum+(m-u+1)*i <= n; i++) {arr[u] = i;dfs(u + 1,i,sum+i);arr[u] = 0;}}
int main() {ios::sync_with_stdio(false);cin.tie(NULL); cout.tie(NULL);cin >> n >> m;dfs(1,1,0);cout << counts << endl;return 0;
}相关文章:

洛谷 1025.数的划分
这道题用的知识点是DFS剪枝。难的不在DFS上,而是在剪枝上如何选择。 思路:这道题我们看到是按照字典序排的,但是,我们注意到,看似是全排列的递归,实则不是。 我们前面也了解过,全排列的数字大…...

MySQL实战:SQL优化及问题排查
有更合适的索引不走,怎么办? MySQL在选取索引时,会参考索引的基数,基数是MySQL估算的,反映这个字段有多少种取值,估算的策略为选取几个页算出取值的平均值,再乘以页数,即为基数 查…...

加密与安全_使用Java代码操作RSA算法生成的密钥对
文章目录 Pre概述什么是非对称加密算法?如何工作?示例:RSA算法特点和优势ECC:另一种非对称加密算法 Code生成公钥和私钥私钥加密私钥加密私钥解密 ( 行不通 )私钥加密公钥解密公钥加密和公钥解密 (行不通)保…...

Spring Boot中实现图片上传功能的两种策略
🌟 前言 欢迎来到我的技术小宇宙!🌌 这里不仅是我记录技术点滴的后花园,也是我分享学习心得和项目经验的乐园。📚 无论你是技术小白还是资深大牛,这里总有一些内容能触动你的好奇心。🔍 &#x…...

07.axios封装实例
一.简易axios封装-获取省份列表 1. 需求:基于 Promise 和 XHR 封装 myAxios 函数,获取省份列表展示到页面 2. 核心语法: function myAxios(config) {return new Promise((resolve, reject) > {// XHR 请求// 调用成功/失败的处理程序}) …...
【Linux】第四十一站:线程控制
一、Linux线程VS进程 1.进程和线程 进程是资源分配的基本单位线程是调度的基本单位线程共享进程数据,但也拥有自己的一部分数据:线程ID一组寄存器(上下文)栈errno信号屏蔽字调度优先级 2.进程的多个线程共享 同一地址空间,因此Text Segment、…...
ChatGPT提示词工程:prompt和chatbot
ChatGPT Prompt Engineering for Developers 本文是 https://www.deeplearning.ai/short-courses/chatgpt-prompt-engineering-for-developers/ 这门课程的学习笔记。 ChatGPT提示词工程:prompt和chatbot 文章目录 ChatGPT Prompt Engineering for DevelopersWhat …...
java算法
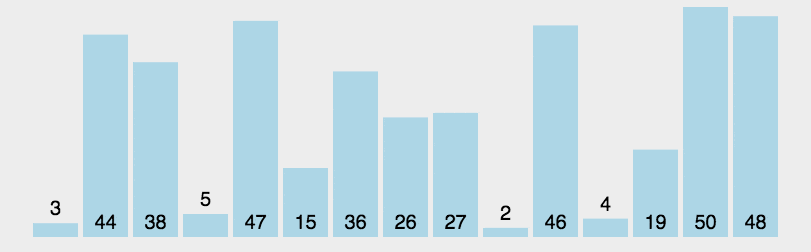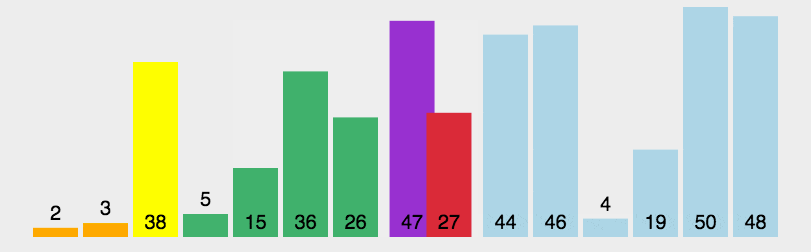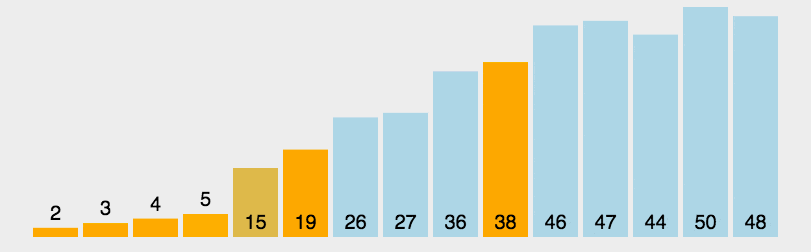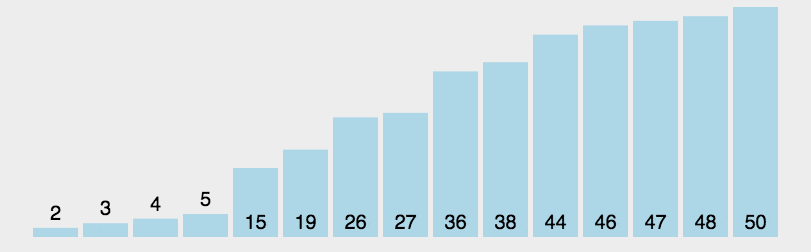
常见的七种查找算法: 数据结构是数据存储的方式,算法是数据计算的方式。所以在开发中,算法和数据结构息息相关。 1. 基本查找 也叫做顺序查找 说明:顺序查找适合于存储结构为数组或者链表。 基本思想:顺序查找也称…...

铭文资产是比特币生态破局者 or 短暂热点?
比特币作为加密货币的鼻祖,一直以来都扮演着数字资产市场的引领者角色。最近几年,随着 BRC20 项目的兴起,我们看到了更多与比特币相互关联的创新。在比特币生态中,BRC20 项目不仅仅是数字资产的代表,更是一种对于区块链…...
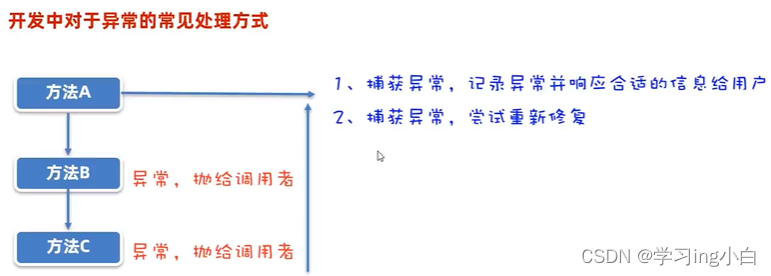
Java基础 - 8 - 算法、正则表达式、异常
一. 算法 什么是算法? 解决某个实际问题的过程和方法 学习算法的技巧? 先搞清楚算法的流程,再直接去推敲如何写算法 1.1 排序算法 1.1.1 冒泡排序 每次从数组中找出最大值放在数组的后面去 public class demo {public static void main(S…...

gRPC-第二代rpc服务
在如今云原生技术的大环境下,rpc服务作为最重要的互联网技术,蓬勃发展,诞生了许多知名基于rpc协议的框架,其中就有本文的主角gRPC技术。 一款高性能、开源的通用rpc框架 作者作为一名在JD实习的Cpper,经过一段时间的学…...

Node.js是什么?
概念:Node.js1运行在服务器端的js,用来编写服务器 特点:单线程、异步、非阻塞、统一API 是一个构建在V8引擎之上的js运行环境,它使得js可以运行在浏览器以外的地方,相对于大部分的服务器端语言来说,Node.J…...
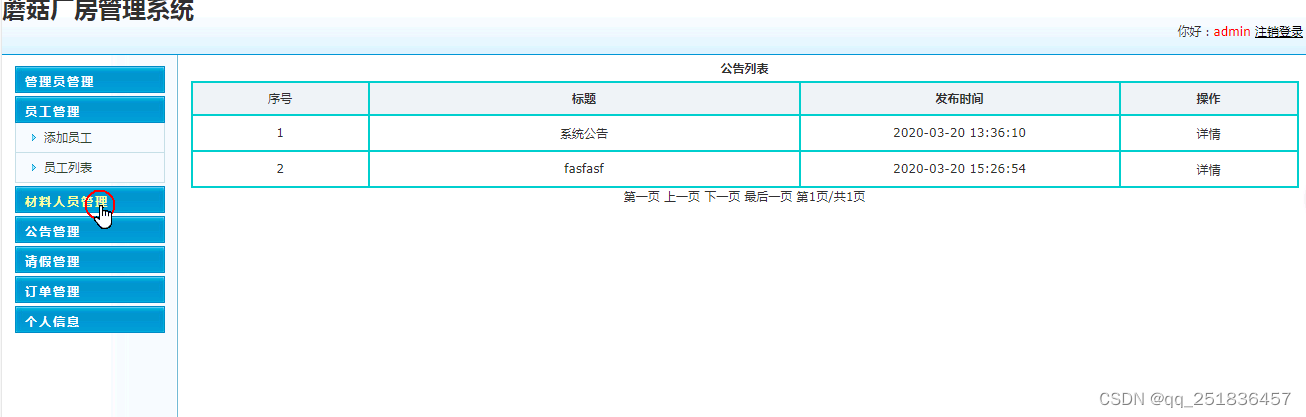
java SSM厂房管理系统myeclipse开发mysql数据库springMVC模式java编程计算机网页设计
一、源码特点 java SSM厂房管理系统是一套完善的web设计系统(系统采用SSM框架进行设计开发,springspringMVCmybatis),对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S…...
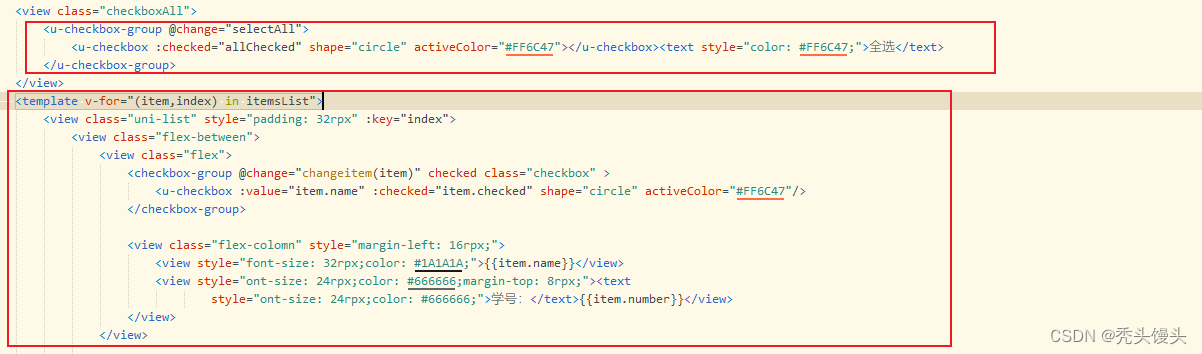
uniapp实现---类似购物车全选
目录 一、实现思路 二、实现步骤 ①view部分展示 ②JavaScript 内容 ③css中样式展示 三、效果展示 四、小结 注意事项 一、实现思路 点击商家复选框,可选中当前商家下的所有商品。点击全选,选中全部商家的商品 添加单个多选框,在将多选…...

Java:List列表去重有序和无序
目录 待去重列表HashSet去重(不保证顺序)TreeSet去重(不保证顺序)LinkedHashSet去重(保证顺序)遍历List去重(保证顺序)Java8中Stream流处理(保证顺序)参考文章 待去重列表 // 列表 …...
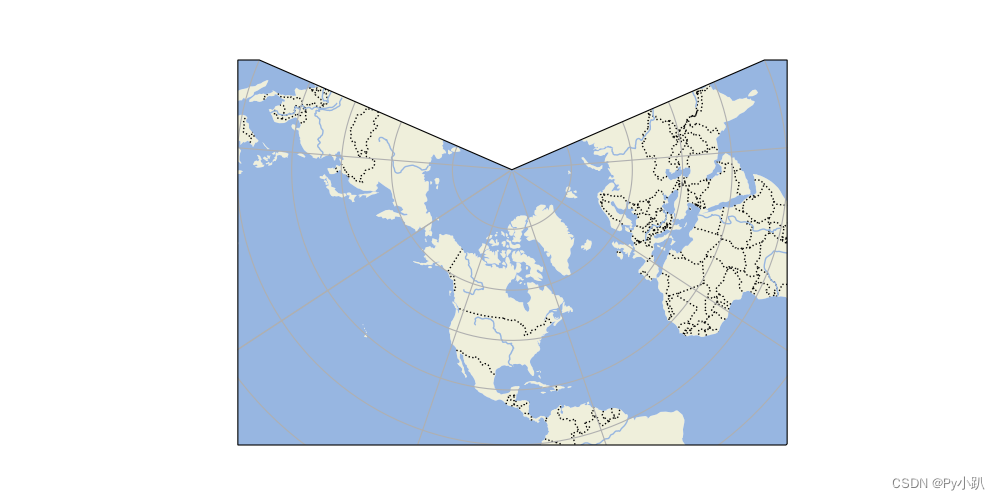
Python绘图-12地理数据可视化
Matplotlib 自 带 4 类别 地理投影: Aitoff, Hammer, Mollweide 及 Lambert 投影,可以 结 合以下四 张 不同 的 图 了解四 种 不同投影 区别 。 12.1Aitoff投影 12.1.1图像呈现 12.1.2绘图代码 import numpy as np # 导入numpy库,用于…...

NineData与OceanBase完成产品兼容认证,共筑企业级数据库新生态
近日,云原生智能数据管理平台 NineData 和北京奥星贝斯科技有限公司的 OceanBase 数据库完成产品兼容互认证。经过严格的联合测试,双方软件完全相互兼容、功能完善、整体运行稳定且性能表现优异。 此次 NineData 与 OceanBase 完成产品兼容认证…...

旅游专业VR虚拟仿真情景教学实训
一、生动的情景模拟 VR技术能够创建出高度逼真的虚拟环境,使学生能够身临其境地体验旅游场景。无论是古色古香的古代建筑,还是充满异国情调的热带雨林,亦或是繁华的都市风光,VR都能一一呈现。这种沉浸式的体验,使得学…...

解决方案TypeError: string indices must be integers
文章目录 一、现象:二、解决方案 一、现象: PyTorch深度学习框架,运行bert-mini,本地环境是torch1.4-gpu,发现报错显示:TypeError: string indices must be integers 后面报字符问题,百度过找…...

【论文阅读】Segment Anything论文梳理
Abstract 我们介绍了Segment Anything(SA)项目:新的图像分割任务、模型和数据集。高效的数据循环采集,使我们建立了迄今为止最大的分割数据集,在1100万张图像中,共超过10亿个掩码。 该模型被设计和训练为可…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
