c++ 常用的STL
前言
写这篇博客目的是为了记录在刷算法题中使用过的STL,因为有些不太常用的会遗忘。这篇博客只是作为笔记,不是详细的STL,因此只会对常用方法说明,不会详细介绍。此外在后面用到新的STL内容时会再补充。
列队
基础列队
基本列队是queue,其中主要有入队、出队、读取队尾或则队首元素、获取队列长度这几个方法。
| 方法 | 说明 |
|---|---|
| pop() | 删除首元素 |
| push() | 添加一个元素 |
| front() | 获取队首元素 |
| back() | 获取队尾元素 |
| size() | 队列长度 |
| empty() | 判断是否为空 |
这里是基础列队queue,有的时候在写算法时为了满足某些需要。需要队列可以弹出队尾元素。这里queue并没有提供相应的方法,当然如果需要可以使用迭代器的 erase() 方法,该方法目的是删除某个元素,并将后面元素前移。
双端操作列队
这里可以使用修改版的列队deque,该列队提供了更加多样的操作,使得列队可以在任何端进行插入和删除操作。这里deque相比于vector优势是速度快一点。
| 方法 | 说明 |
|---|---|
| pop_front() | 删除队首元素 |
| pop_back() | 删除队尾元素 |
| push_front() | 队首添加一个元素 |
| push_back() | 队尾添加一个元素 |
| front() | 获取队首元素 |
| back() | 获取队尾元素 |
| size() | 队列长度 |
| empty() | 判断是否为空 |
向量数组
向量数组vector,向量数组相比于传统的数组,优势在于其长度可以动态扩展,而不必一开始就规定数组大小。并直接提供了队尾添加删除操作。
| 方法 | 说明 |
|---|---|
| pop_back() | 删除尾元素 |
| push_back() | 向尾部添加一个元素 |
| front() | 获取首元素 |
| back() | 获取尾元素 |
| size() | 队列长度 |
| empty() | 获取数组长度 |
例如代码:
#include<bits/stdc++.h>
using namespace std;
int main(){vector<int> a;for(int i=0;i<10;i++)a.push_back(i);a.pop_back();for(int i=0;i<a.size();i++){cout<<a[i]<<' ';}cout<<endl<<a.size();
}
结果是:

这里经常配合使用的方法是**unique(a,b)**该方法是将重复元素移动到数组尾部,参数分别是开始和结束部分迭代器。返回不重复部分最后一个元素的迭代器。
集合
集合特点是自动排序,并且集合没有重复元素。集合没有提供按元素查找方式,可以通过迭代器实现,具体实现看这篇博客。
基础集合
基础集合是set 该集合不允许出现重复元素(出现相同元素会被覆盖)。默认按照升序排序。也可以指定排序方式。
| 方法 | 说明 |
|---|---|
| size() | 集合元素个数 |
| insert() | 插入元素 |
| empty() | 集合是否为空 |
| find() | 查找元素,返回迭代器 |
#include<bits/stdc++.h>
using namespace std;
struct cmp{bool operator()(const int&a,const int&b){if(a<b)return false;return true;}
};//定义的排序方法
int main(){set<int,cmp> m; //按照定义进行排序set<int>::iterator iters;m.insert(1);m.insert(9);iters=m.begin();cout<<*iters<<' ';cout<<m.size();
}
结果是
9 2
可重复集合
可重复集合是multiset,该集合区别是可以重复存储相同元素。不会覆盖,除此之外方法等和set基本没什么区别。
映射
映射是map,映射通过键值对一一映射,从而可以快速查询数据。一般来说使用时和数组差不多。没什么很多方法,如果一个键值对不存在,并查询一个不存在的键时,如果值类型是整形,则其值等于0
#include<bits/stdc++.h>
using namespace std;
int main(){map<int,int> m;m[1]=100;m[2]++;cout<<m[1]<<' '<<m[2]<<' '<<m[3]<<endl;
}
结果为:
pair
pair是将两个数据组成一个元素,其中这两个数据类型可以是不同类型。主要通过first访问第一个数据元素,通过second访问第二个数据元素。
#include<bits/stdc++.h>
using namespace std;
int main(){pair<int,char> a;a.first=4;a.second='a';cout<<a.first<<' '<<a.second;
}
结果为

迭代器
迭代器类似于指针,对于上述数据类型。都可以获取其相应的迭代器。如果c++版本够高可以直接使用auto接收返回的迭代器。不过我的c++版本太低只能自己定义。其定义方式是数据类型::iterator 迭代器名.具体如下如下:
定义一个map<int,int>名为iters的迭代器:
map<int,int>::iterator iters
在上述类型中一般使用如下获取相应迭代器
| 方法 | 说明 |
|---|---|
| begin() | 指向第一个元素迭代器 |
| end() | 最后的迭代器 |
这两个方法是通用的,有些数据类型也提供其他放回迭代器的方法,例如set的find()方法,返回一个指向目标元素的迭代器。迭代器访问是通过*迭代器变量名。
迭代器向前移动可以通过方法advance(iters,steps)参数分别是迭代器名和向前移动步数。
#include<bits/stdc++.h>
using namespace std;
int main(){deque<int> a;deque<int>::iterator iters; //deque<int>类型迭代器for(int i=0;i<10;i++){a.push_back(i);}iters=a.begin(); //获取指向第一个元素的迭代器for(int i=0;i<a.size();i++){cout<<*iters<<' ';advance(iters,1); //迭代器向前移动一个元素}
}
结果为
删除方法是erase()该方法将迭代器指向元素删除,并将后面元素向前移动。
例如代码
#include<bits/stdc++.h>
using namespace std;
int main(){deque<int> a;deque<int>::iterator iters; for(int i=0;i<10;i++){a.push_back(i);}iters=a.begin();a.erase(iters);iters=a.begin();cout<<*iters<<endl;
结果为;

相关文章:

c++ 常用的STL
前言 写这篇博客目的是为了记录在刷算法题中使用过的STL,因为有些不太常用的会遗忘。这篇博客只是作为笔记,不是详细的STL,因此只会对常用方法说明,不会详细介绍。此外在后面用到新的STL内容时会再补充。 列队 基础列队 基本列…...

接口自动化测试思路和实战 —— 编写线性测试脚本实战!
接口自动化测试框架目的 测试工程师应用自动化测试框架的目的: 增强测试脚本的可维护性、易用性(降低公司自动化培训成本,让公司的测试工程师都可以开展自动化测试)。 自动化测试框架根据思想理念和深度不同,渐进式的分为以下几种: 线性脚本框架 模块…...

python控制语句-1.2
目录 循环结构 while循环 for循环 循环结构练习-1 循环嵌套 循环结构练习-2 循环控制语句(continue & break) 循环结构 while循环 语法 Python 编程中 while 语句用于循环执行程序,即在某条件下,循环执行某段程序&am…...

HTML 学习笔记(一)开始
一、介绍: 首先引用百度百科的一段话作为介绍: HTML的全称为超文本标记语言,是一种标记语言。它包括一系列标签,通过这些标签可以将网络上的文档格式统一,使分散的Internet资源连接为一个逻辑整体。HTML文本是由HTML命令组成的描述性文本…...

查看自己的ip地址的网站
有时候需要知道自己的ip地址,可以上这个网站查看: What Is My IP? Best Way To Check Your Public IP Address 网站的域名是https://www.whatismyip.com/ 还是挺好记的。...

ES分布式搜索-索引库操作
索引库操作 1、mapping映射属性 可以查看官方文档学习:ES官方手册 mapping是对索引库中文档的约束,常见的mapping属性包括: type:字段数据类型,常见的简单类型有: 字符串:text(可…...
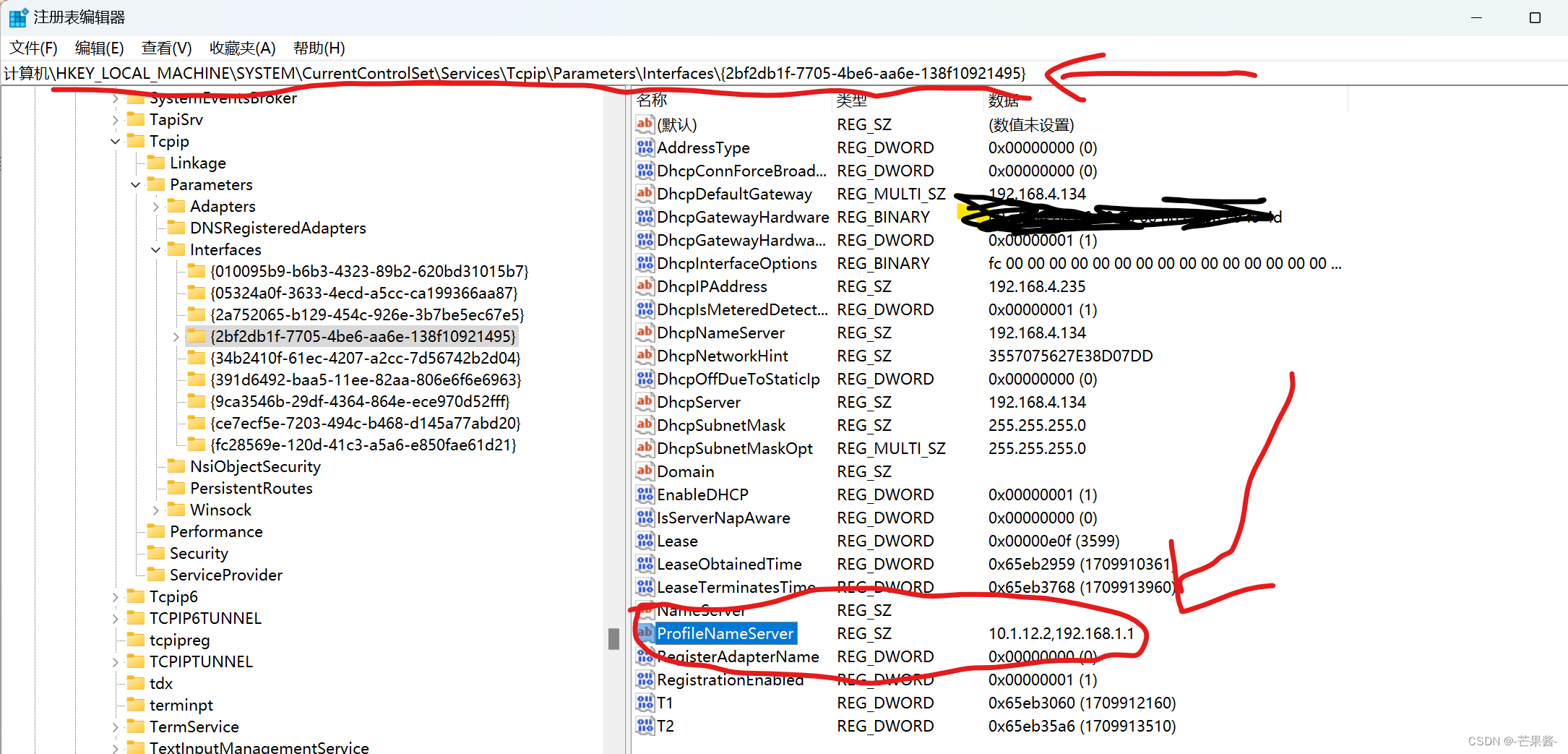
Win11 没有网络bug
1.问题描述 没有网络,dns一直是固定的,但是dns已经是自动获取了(MAC地址随机) 2.解决办法 1.首先,删除所有网络的手动dns配置,控制中心那个dns管理没有用,在设置中删除网络,不然问题还会出现 - 2.然后,进入注册表\HKEY_LOCAL_MACH…...

洛谷 1025.数的划分
这道题用的知识点是DFS剪枝。难的不在DFS上,而是在剪枝上如何选择。 思路:这道题我们看到是按照字典序排的,但是,我们注意到,看似是全排列的递归,实则不是。 我们前面也了解过,全排列的数字大…...

MySQL实战:SQL优化及问题排查
有更合适的索引不走,怎么办? MySQL在选取索引时,会参考索引的基数,基数是MySQL估算的,反映这个字段有多少种取值,估算的策略为选取几个页算出取值的平均值,再乘以页数,即为基数 查…...

加密与安全_使用Java代码操作RSA算法生成的密钥对
文章目录 Pre概述什么是非对称加密算法?如何工作?示例:RSA算法特点和优势ECC:另一种非对称加密算法 Code生成公钥和私钥私钥加密私钥加密私钥解密 ( 行不通 )私钥加密公钥解密公钥加密和公钥解密 (行不通)保…...

Spring Boot中实现图片上传功能的两种策略
🌟 前言 欢迎来到我的技术小宇宙!🌌 这里不仅是我记录技术点滴的后花园,也是我分享学习心得和项目经验的乐园。📚 无论你是技术小白还是资深大牛,这里总有一些内容能触动你的好奇心。🔍 &#x…...

07.axios封装实例
一.简易axios封装-获取省份列表 1. 需求:基于 Promise 和 XHR 封装 myAxios 函数,获取省份列表展示到页面 2. 核心语法: function myAxios(config) {return new Promise((resolve, reject) > {// XHR 请求// 调用成功/失败的处理程序}) …...
【Linux】第四十一站:线程控制
一、Linux线程VS进程 1.进程和线程 进程是资源分配的基本单位线程是调度的基本单位线程共享进程数据,但也拥有自己的一部分数据:线程ID一组寄存器(上下文)栈errno信号屏蔽字调度优先级 2.进程的多个线程共享 同一地址空间,因此Text Segment、…...
ChatGPT提示词工程:prompt和chatbot
ChatGPT Prompt Engineering for Developers 本文是 https://www.deeplearning.ai/short-courses/chatgpt-prompt-engineering-for-developers/ 这门课程的学习笔记。 ChatGPT提示词工程:prompt和chatbot 文章目录 ChatGPT Prompt Engineering for DevelopersWhat …...
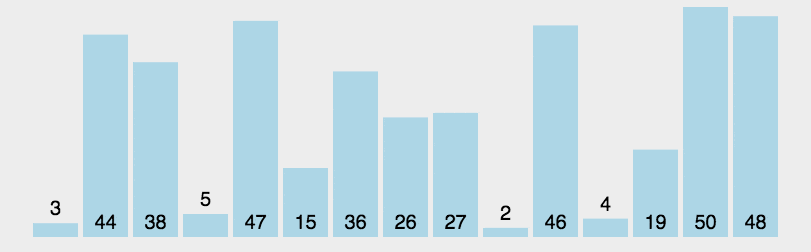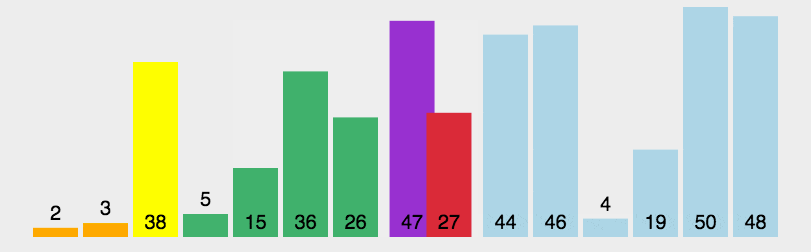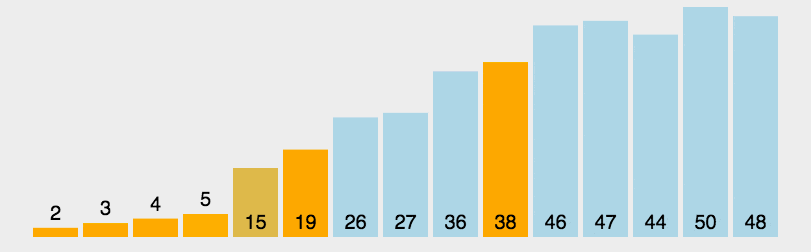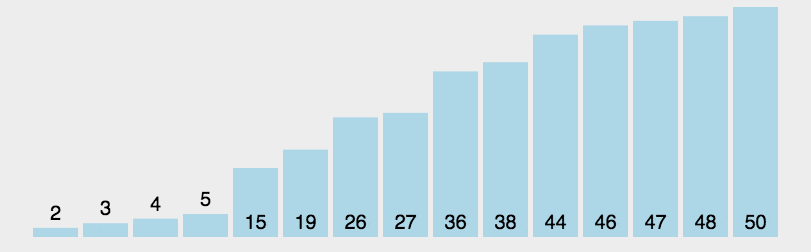
java算法
常见的七种查找算法: 数据结构是数据存储的方式,算法是数据计算的方式。所以在开发中,算法和数据结构息息相关。 1. 基本查找 也叫做顺序查找 说明:顺序查找适合于存储结构为数组或者链表。 基本思想:顺序查找也称…...

铭文资产是比特币生态破局者 or 短暂热点?
比特币作为加密货币的鼻祖,一直以来都扮演着数字资产市场的引领者角色。最近几年,随着 BRC20 项目的兴起,我们看到了更多与比特币相互关联的创新。在比特币生态中,BRC20 项目不仅仅是数字资产的代表,更是一种对于区块链…...
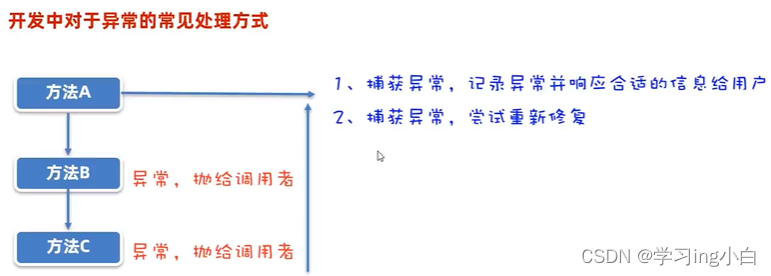
Java基础 - 8 - 算法、正则表达式、异常
一. 算法 什么是算法? 解决某个实际问题的过程和方法 学习算法的技巧? 先搞清楚算法的流程,再直接去推敲如何写算法 1.1 排序算法 1.1.1 冒泡排序 每次从数组中找出最大值放在数组的后面去 public class demo {public static void main(S…...

gRPC-第二代rpc服务
在如今云原生技术的大环境下,rpc服务作为最重要的互联网技术,蓬勃发展,诞生了许多知名基于rpc协议的框架,其中就有本文的主角gRPC技术。 一款高性能、开源的通用rpc框架 作者作为一名在JD实习的Cpper,经过一段时间的学…...

Node.js是什么?
概念:Node.js1运行在服务器端的js,用来编写服务器 特点:单线程、异步、非阻塞、统一API 是一个构建在V8引擎之上的js运行环境,它使得js可以运行在浏览器以外的地方,相对于大部分的服务器端语言来说,Node.J…...
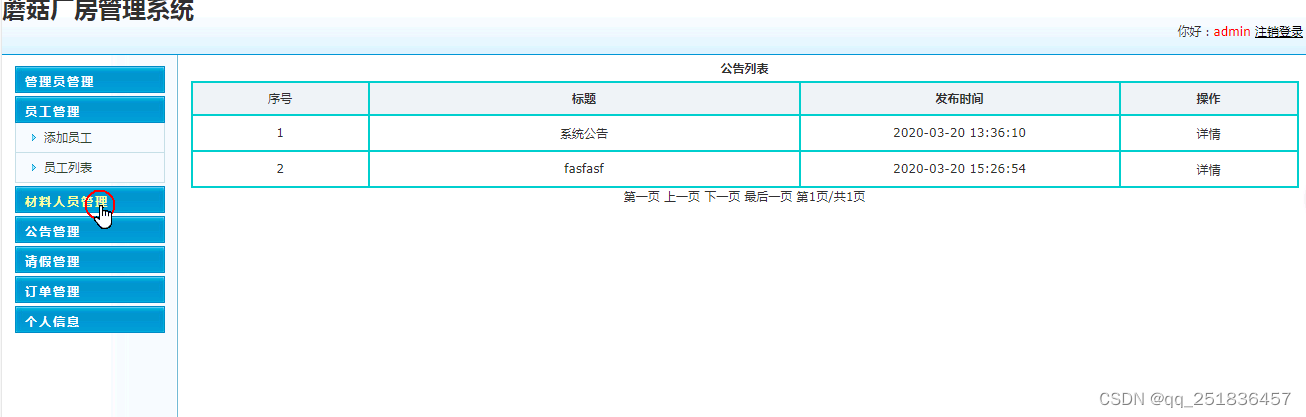
java SSM厂房管理系统myeclipse开发mysql数据库springMVC模式java编程计算机网页设计
一、源码特点 java SSM厂房管理系统是一套完善的web设计系统(系统采用SSM框架进行设计开发,springspringMVCmybatis),对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
