数据结构与算法-希尔排序
引言
在计算机科学中,数据结构和算法是构建高效软件系统的基石。而排序算法作为算法领域的重要组成部分,一直在各种应用场景中发挥着关键作用。今天我们将聚焦于一种基于插入排序的改进版本——希尔排序(Shell Sort),深入了解其原理、实现步骤以及优缺点。
一、希尔排序简介
希尔排序(Shell Sort) 是由Donald Shell在1959年提出的,它是对插入排序的一种改进,通过定义一个增量序列来对原始数据进行分组和预处理,使得每组内的数据相对有序,然后逐步减小增量并最终采用插入排序将所有数据完全排序。
二、希尔排序详细步骤
-
初始化增量序列:希尔排序的核心在于使用一系列的间隔(或称增量)对数组进行划分,初始时通常选择一个较大的间隔序列,例如
n/2, n/4, ..., 1(这里的n是数组长度)。 -
按增量分组排序:对于每一个增量值,将数组划分为多个子序列,每个子序列内部执行插入排序。例如,当增量为
gap时,将从索引0到gap-1的元素作为一个子序列,然后是gap到2gap-1的元素,以此类推。 -
递减增量继续排序:重复上述过程,但每次减少一个增量,直到增量为1,此时整个数组被当作一个子序列进行插入排序,完成最后的排序工作。
三、希尔排序的时间复杂度与空间复杂度分析
-
时间复杂度:希尔排序的时间复杂度取决于增量序列的选择,理论上最佳情况下可以达到O(n log n),但在实际应用中由于难以找到理想的增量序列,一般认为其平均时间复杂度介于O(n^1.3)到O(n^2)之间。
-
空间复杂度:希尔排序是原地排序算法,不需要额外的存储空间,因此其空间复杂度为O(1)。
四、希尔排序的优缺点
优点:
- 相比于简单插入排序,希尔排序能显著提升对大规模无序数据集的排序效率。
- 空间效率高,适合内存资源有限的情况。
缺点:
- 时间复杂度依赖于增量序列的选择,如果增量序列选择不当,可能会导致效率降低。
- 希尔排序并不是稳定的排序算法,相等元素的顺序可能在排序过程中发生变化。
五、希尔排序的图解过程
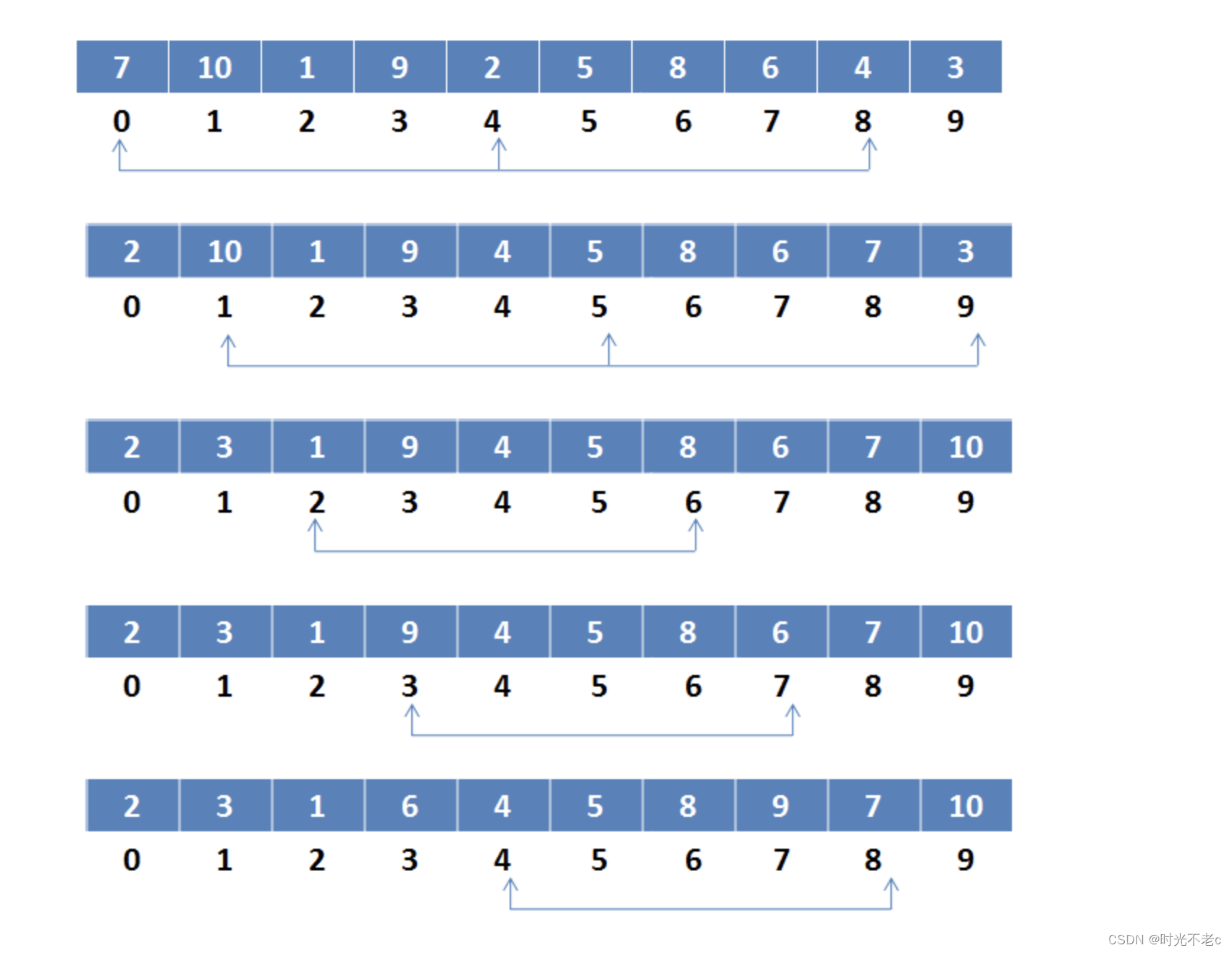
图解小结
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序,随着增了逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个数据恰被分为一组,算法便终止进行了。
六、希尔排序的代码实践
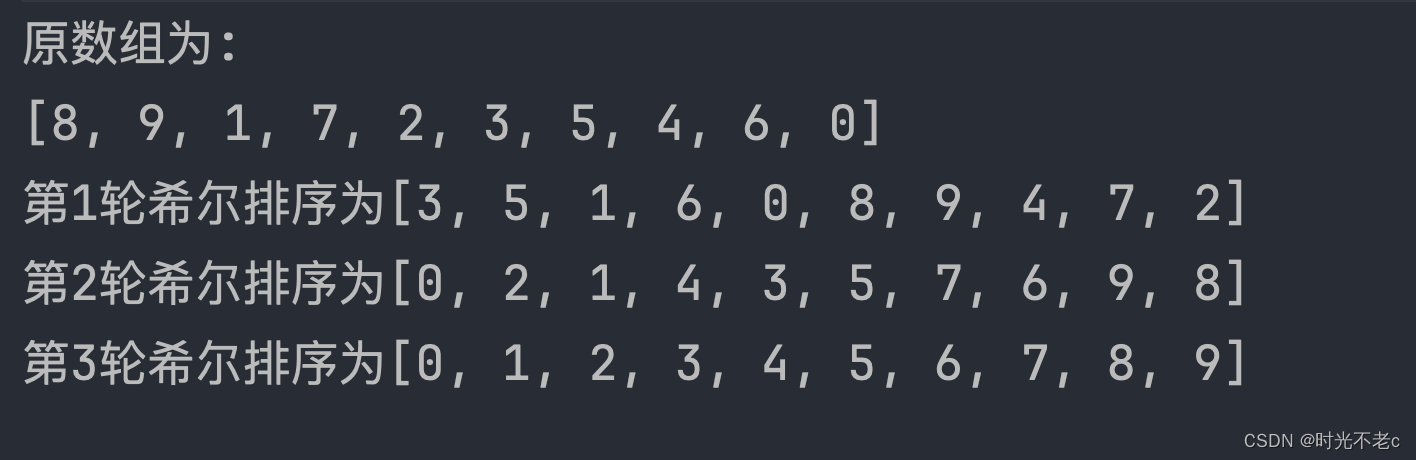
1.展示每一次选择排序过程
// 第一轮
// 应为第一轮排序是将10个数据分成了10 /2 = 五组for (int i = 5; i < arr.length; i++) {
// 遍历各组中所有的元素(共有5组,每组两个元素,步长5)for (int j = i - 5; j >= 0; j -= 5) {
// 如果当前元素大于加上步长后的那个元素,说明需要交换if (arr[j] > arr[j + 5]) {int temp = arr[j];arr[j] = arr[j + 5];arr[j + 5] = temp;}}}System.out.println("第一轮希尔排序为");System.out.println(Arrays.toString(arr));// 第二轮
// 应为第二轮排序是将10个数据分成了5 /2 = 2组for (int i = 2; i < arr.length; i++) {
// 遍历各组中所有的元素(共有5组,每组两个元素,步长5)for (int j = i - 2; j >= 0; j -= 2) {
// 如果当前元素大于加上步长后的那个元素,说明需要交换if (arr[j] > arr[j + 2]) {int temp = arr[j];arr[j] = arr[j + 2];arr[j + 2] = temp;}}}System.out.println("第二轮希尔排序为");System.out.println(Arrays.toString(arr));// 第一轮
// 应为第一轮排序是将10个数据分成了2 /2 =1组for (int i = 1; i < arr.length; i++) {
// 遍历各组中所有的元素(共有5组,每组两个元素,步长5)for (int j = i - 1; j >= 0; j -= 1) {
// 如果当前元素大于加上步长后的那个元素,说明需要交换if (arr[j] > arr[j + 1]) {int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}System.out.println("第三轮希尔排序为");System.out.println(Arrays.toString(arr));2.总结规律得到过程
public static void shellSort(int[] arr) {
// 有上述可得规律int temp = 0;int count = 0;for (int gap = arr.length / 2; gap > 0; gap /= 2) {count++;for (int i = gap; i < arr.length; i++) {
// 遍历各组中的元素共有gap组,步长为gapfor (int j = i - gap; j >= 0; j -= gap) {if (arr[j] > arr[j + gap]) {temp = arr[j];arr[j] = arr[j + gap];arr[j + gap] = temp;}}}System.out.printf("第%d轮希尔排序为", count);System.out.println(Arrays.toString(arr));}}七、总结
虽然希尔排序在理论上的性能不如快速排序、归并排序等高级排序算法,但由于其简单且易于实现的特点,在某些特定场景下仍具有一定的实用价值,比如在硬件资源有限的嵌入式系统中,或者需要快速实现一个基础排序功能时。
希尔排序是一种早期出现的改进型排序算法,它的提出启示我们可以通过对传统算法进行改良以适应不同的需求场景。尽管希尔排序在现代排序算法家族中并非最优解,但它在理解排序算法优化思路、探索更高效排序策略等方面依然具有重要的学习和研究价值。同时,希尔排序也是我们在实际编程中根据具体问题灵活选择排序算法的一个良好例证。
相关文章:

数据结构与算法-希尔排序
引言 在计算机科学中,数据结构和算法是构建高效软件系统的基石。而排序算法作为算法领域的重要组成部分,一直在各种应用场景中发挥着关键作用。今天我们将聚焦于一种基于插入排序的改进版本——希尔排序(Shell Sort),深…...

蓝桥杯算法错题记录
这里写目录标题 本文还在跟新,最新更新时间24/3/91. nextInt () next() nextLine() 的注意事项2 . 转换数据类型int ,string,charint -> string , charstring -> int ,charchar -> int , string 进制转换十六进制转化为10 进制 最大公约数 本文还在跟新&am…...

【Python 图像处理 PIL 系列 13 -- PIL 及 Image.convert 函数介绍】
文章目录 Python PIL 介绍PIL 使用介绍PIL convert 介绍PIL convert 使用示例 Python PIL 介绍 PIL 是 Python Image Library 的简称。PIL 库中提供了诸多用来处理图片的模块,可以对图片做类似于 PS(Photoshop) 的编辑。比如:改变…...

使用docker datascience-notebook进行数据分析
Jupyter/datascience-notebook 简介 jupyter/datascience-notebook 是 Docker Hub 上可用的 Docker 镜像:https://hub.docker.com/。该镜像提供了一个开箱即用的环境,用于数据科学任务,包括: Jupyter Notebook: 一个基于 Web 的…...
VR全景技术在VR看房中有哪些应用,能带来哪些好处
引言: 随着科技的不断发展,虚拟现实(VR)技术在房地产行业中的应用也越来越广泛。其中,VR全景技术在VR看房中的运用尤为突出。今天,让我们一起深入探讨VR全景技术在VR看房中的应用及其带来的种种好处。 一、…...
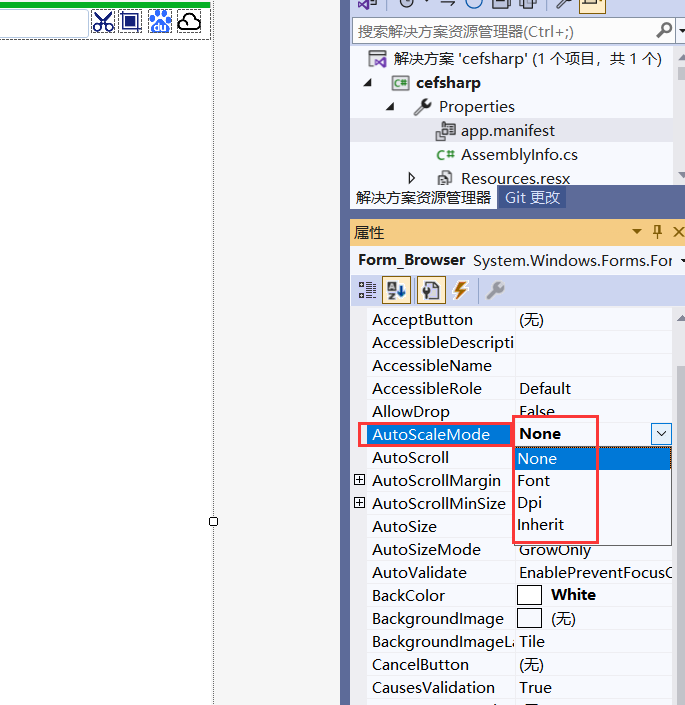
Winform窗体随着屏幕的DPI缩放,会引起窗体变形及字体变形,superTabControl标签字体大小不匹配
一、前言 superTabControl做的浏览器标签(cefsharp)在缩放比例(125%,150%时字体不协调) 物联网浏览器,定制浏览器,多媒体浏览器(支持H264)参考栏目文章即可 二、配置参数 app.manifest参数 dpiAware =true <application xmlns="urn:schemas-microsoft-c…...

java网络编程 01 IP,端口,域名,TCP/UDP, InetAddress
01.IP 要想让网络中的计算机能够互相通信,必须为计算机指定一个标识号,通过这个标识号来指定要接受数据的计算机和识别发送的计算机,而IP地址就是这个标识号,也就是设备的标识。 ip地址组成: ip地址分类:…...
第十篇 - 如何利用人工智能技术做好营销流量整形管理?(Traffic Shaping)- 我为什么要翻译介绍美国人工智能科技巨头IAB公司
IAB平台,使命和功能 IAB成立于1996年,总部位于纽约市。 作为美国的人工智能科技巨头社会媒体和营销专业平台公司,互动广告局(IAB- the Interactive Advertising Bureau)自1996年成立以来,先…...

npm ERR! errno -13具体问题处理
npm ERR! errno -13具体问题处理 出现问题的报错 npm ERR! code EACCES npm ERR! syscall open npm ERR! path /Users/xxxx/.npm/_cache/index-v5/c6/06/xxxxx npm ERR! errno -13 npm ERR! npm ERR! Your cache folder contains root-owned files, due to a bug in npm ERR! …...
【Python】3. 基础语法(2) -- 语句篇
顺序语句 默认情况下, Python 的代码执行顺序是按照从上到下的顺序, 依次执行的. print("1") print("2") print("3")执行结果一定为 “123”, 而不会出现 “321” 或者 “132” 等. 这种按照顺序执行的代码, 我们称为 顺序语句. 这个顺序是很关…...
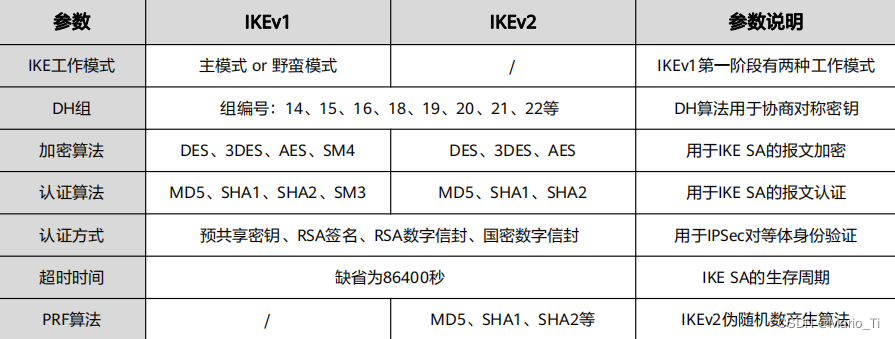
IPsec VPN之安全联盟
一、何为安全联盟 IPsec在两个端点建立安全通信,此时这两个端点被称为IPsec对等体。安全联盟,即SA,是指通信对等体之间对某些要素的约定,定义了两个对等体之间要用何种安全协议、IP报文的封装方式、加密和验证算法。SA是IPsec的基…...

012集——显示高考天数倒计时——vba实现
以下代码实现高考倒计时: Sub 高考倒计时() 高考日期 CDate("06,07," & Year(Date)) If Date > 高考日期 Then高考日期 CDate("06-07-" & Year(Date) 1) End If 年月日 Year(Date) & "年" & Month(Date) &am…...
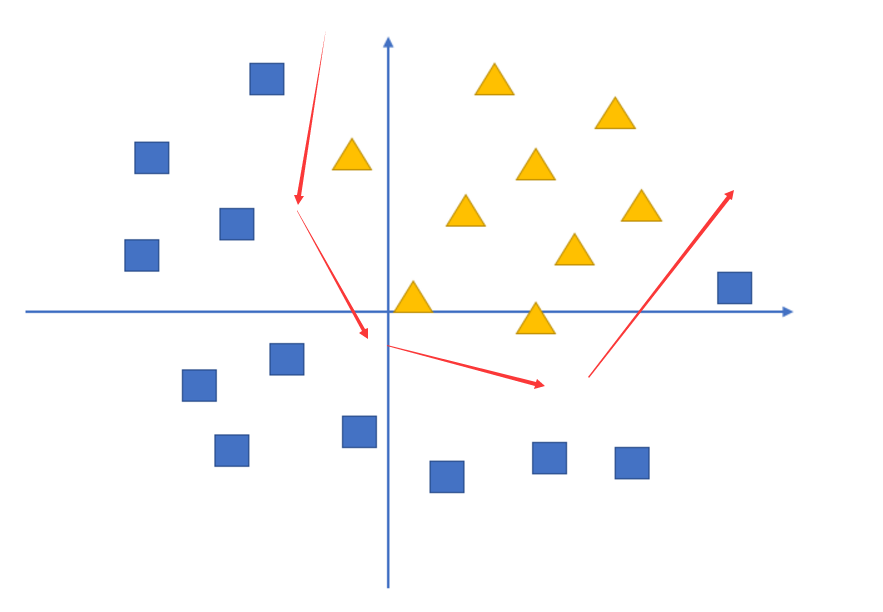
1.1 深度学习和神经网络
首先要说的是:深度学习的内容,真的不难。你要坚持下去。 神经网络 这就是一个神经网络。里面的白色圆圈就是神经元。神经元是其中最小的单位。 神经网络 单层神经网络: 感知机 (双层神经网络) 全连接层: …...

sentinel docker 基础配置学习
1:去官网下载 Releases alibaba/Sentinel GitHub 2:保存到linux 3:编写dockerfile FROM openjdk:8-jreLABEL authors"xxx" #第二步创建一个文件夹Z RUN mkdir /app #第三步复制jar 到app 下 COPY xxxxxx-1.8.7.jar /app/#第四…...

与缓存相关的状态码
与缓存相关的 HTTP 状态码主要涉及客户端和服务器之间对资源缓存的处理和验证,以下是一些常见的与缓存相关的状态码: 1. **200 OK**: - 当服务器成功处理了客户端的请求时,会返回状态码 200 OK。这意味着请求成功,…...

影刀_如何点击桌面图片上的指定区域
问题:如图,桌面上有一张打开的图片,如何点击“J&T极兔快递”的左上角和右下角? 总体流程: 1、用“影刀离线OCR”指令获取目标区域坐标值。 分别是:x1,y1,x2,y2 2、用快捷键ctrlalt键获取图片左上角的…...
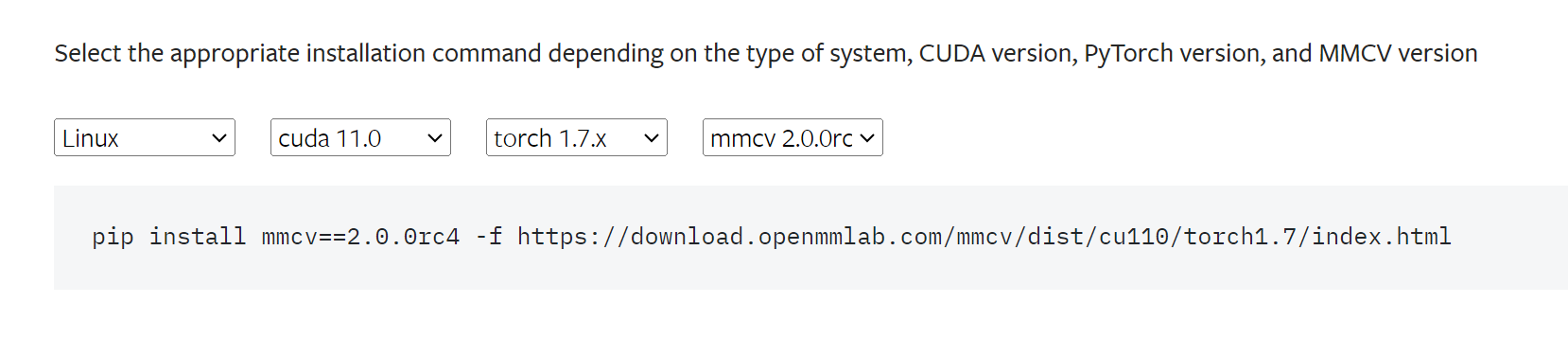
linux安装部署mmdetection,亲测可行
安装了两天,最后终于成功,这里有一些注意事项,版本对应啥的: 这里是mmdetection与MMCV的版本对应关系: mmdet与mmcv的版本对应有一些包因为版本问题直接pip下载不了,这里直接跑到官网去复制下载命令&#…...
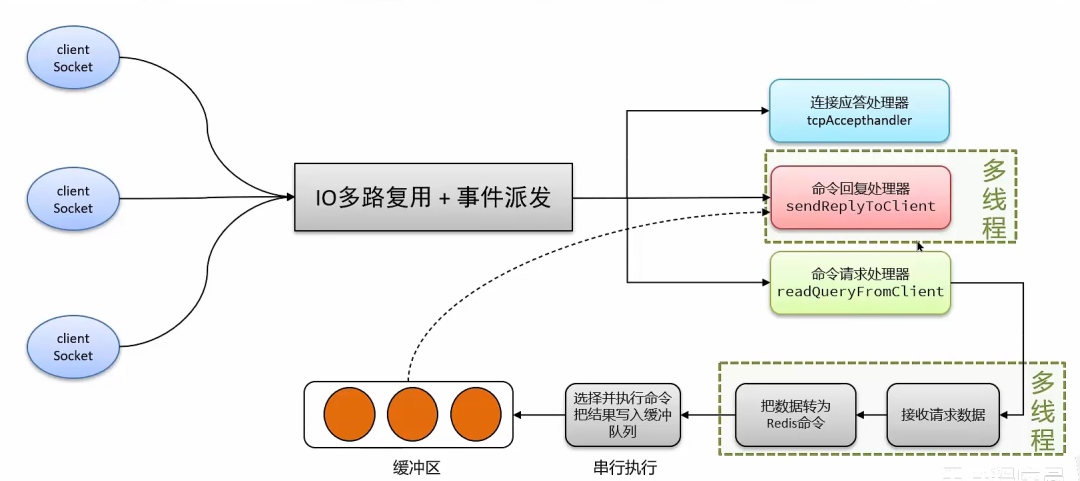
redis常见问题
目录 一、缓存穿透 二、缓存击穿 三、缓存雪崩 四、redis做为缓存,mysql的数据如何与redis进行同步呢?(双写一致性) 五、redis做为缓存,数据的持久化是怎么做的? 六、数据过期策略 七、数据淘汰策略 八、Redis分布式锁使用场景 九、Redis分布…...
元数据区存放的内容)
Java虚拟机(JVM)元数据区存放的内容
类元数据 元数据区(在HotSpot虚拟机中也称为Metaspace)主要存放了类的元数据信息,如类的名称、访问修饰符、常量池、字段描述、方法描述等。 运行时常量池 运行时常量池是每个类或接口的常量池表的运行时表示形式,包含了若干种不…...

wifi连接上后是怎么提供网络的?
干了六个月的网络协议栈,又回到了wifi老本行,所以我最近又开始研读 Android wifi fwk的源码了 之前还在干wifi的时候就思考过一个问题,wifi区别于蓝牙的一个很明显的点是,wifi可以提供 access to Internet 所以我想看看wifi连接成…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
