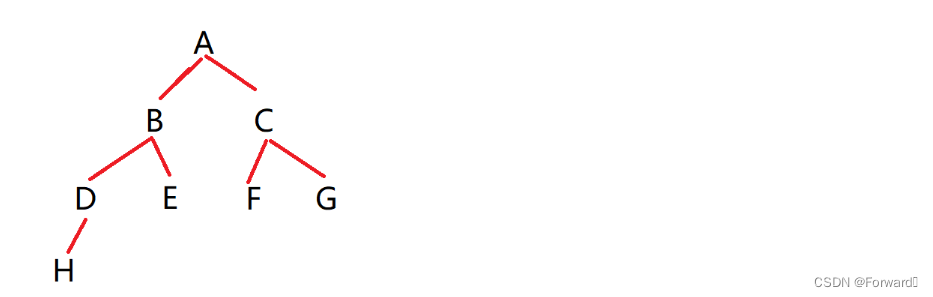二叉树遍历(前中后序的递归/非递归遍历、层序遍历)
二叉树的遍历
1. 二叉树的前序、中序、后序遍历
- 前、中、后序遍历又叫深度优先遍历
- 注:严格来说,深度优先遍历是先访问当前节点再继续递归访问,因此,只有前序遍历是严格意义上的深度优先遍历
- 首先需要知道下面几点:
- 任何一颗二叉树,都由根节点、左子树、右子树构成。
如图:
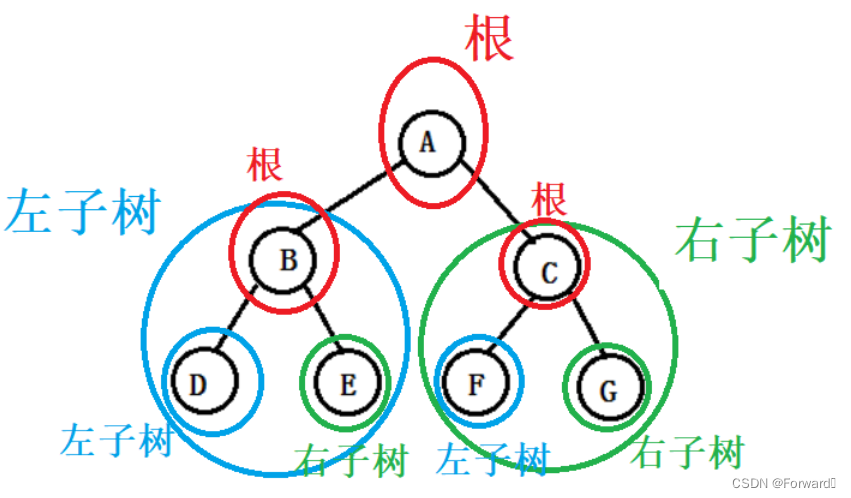
- 分治算法:分而治之。大问题分成类似的子问题,子问题再分成子问题……直到子问题不能再分割。对树也可以做类似的处理,对一棵树不断地分割,直到子树为空时,分割停止。
- 关于二叉树的许多问题我们都要利用分治思想,将一棵完整的树分解成根和左右两棵子树,然后再对这两棵子树进行相同的递归处理,最后得到结果。
- 如果对递归的过程想的不太清楚,建议画递归展开图来辅助理解。
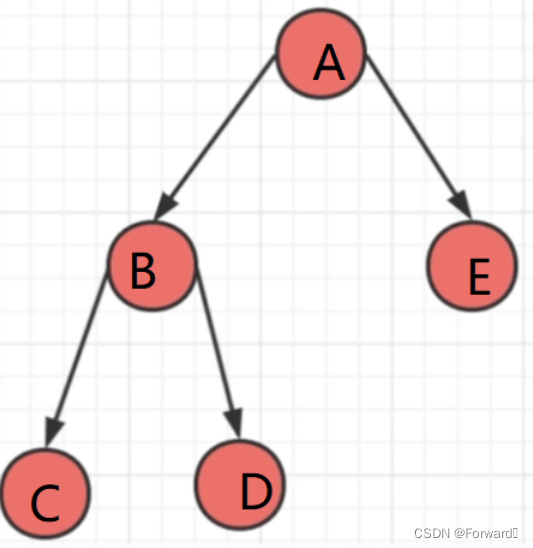
1.1 前序(先根)遍历
-
遍历顺序:根- > 左子树 -> 右子树(即先访问根,再访问左子树,最后在访问右子树)
-
如上图中:A -> B -> C -> NULL -> NULL -> D -> NULL -> NULL -> E -> NULL -> NULL
typedef char BTDataType;
typedef struct BinaryTreeNode
{struct BinaryTreeNode *left; //指向左子树struct BinaryTreeNode *right; //指向右子树BTDataType data;
}BTNode;void PrevOrder(BTNode * root) //前序遍历
{if (!root)return;printf("%d ",root->data); //根PrevOrder(root->left); //左子树PrevOrder(root->right); //右子树return;
}
递归顺序图:
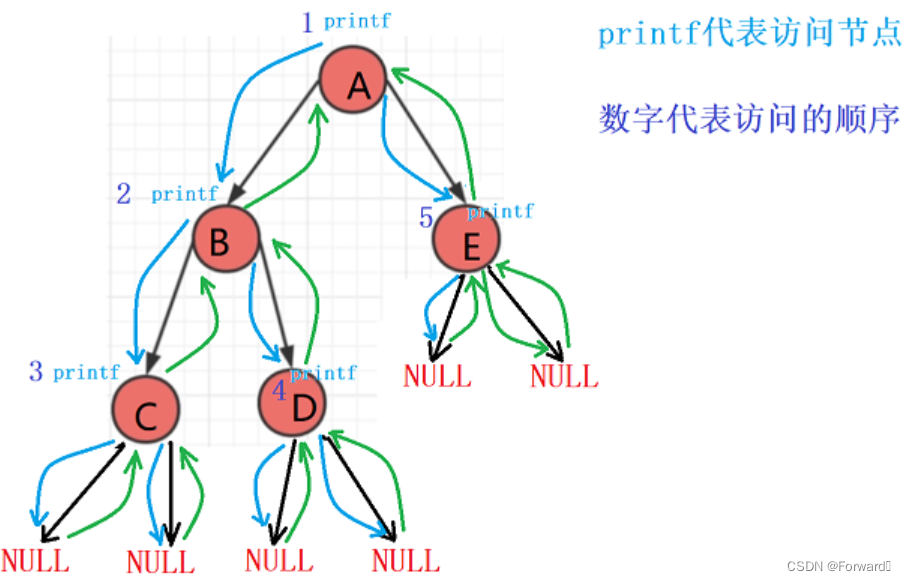
递归展开图:

1.2 中序(中根)遍历
-
遍历顺序:左子树 -> 根 -> 右子树(即先访问左子树,再访问根,最后在访问右子树)
-
如上图中:NULL -> C -> NULL -> B -> NULL -> D -> NULL -> A -> NULL -> E -> NULL
void InOrder(BTNode* root)
{if (!root)return;InOrder(root->left); //左子树printf("%c ", root->data); //根InOrder(root->right); //右子树return;
}
递归顺序图:
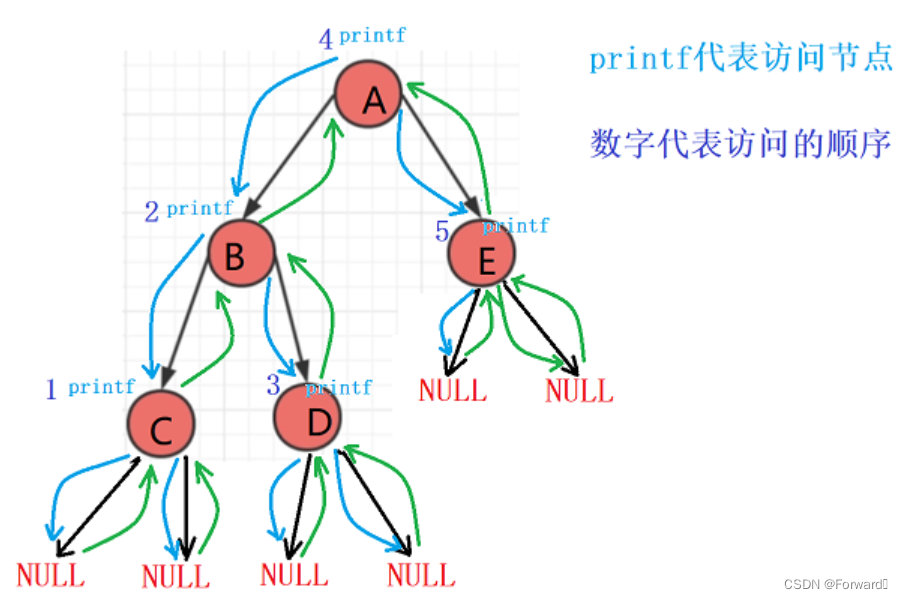
1.3 后序(后根)遍历
-
遍历顺序:左子树 -> 右子树 -> 根(即先访问左子树,再访问左=右子树,最后在访问根)
-
如上图中:NULL -> NULL -> C -> NULL -> NULL -> D -> B -> NULL -> NULL -> E -> A
void PostOrder(BTNode* root)
{if (!root){printf("NULL ");return;}PostOrder(root->left); //左子树PostOrder(root->right); //右子树printf("%c ", root->data); //根
}
递归顺序图:
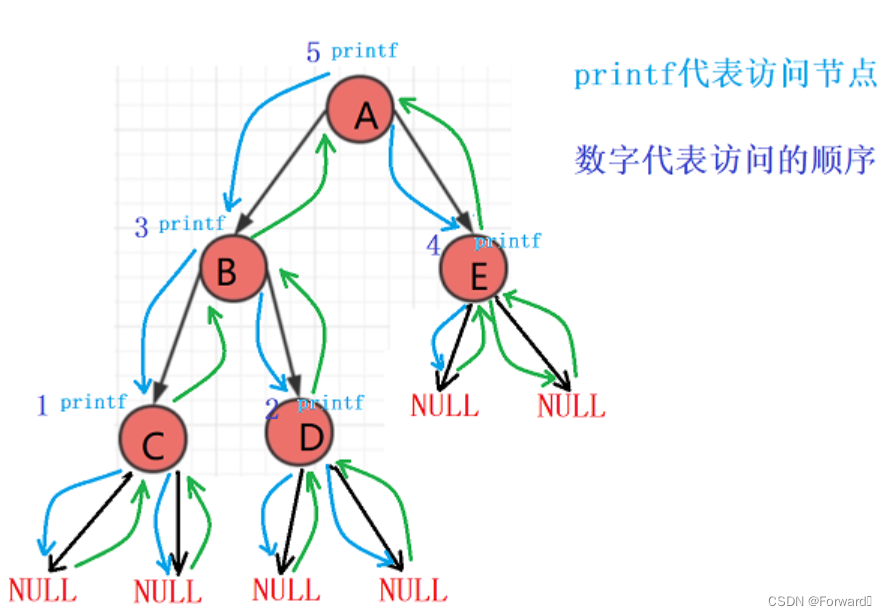
2. 二叉树前中后序的非递归遍历
- 在利用递归来进行二叉树的前中后序遍历时,我们通常将一棵二叉树看成三部分:根、左子树、右子树。
- 但是对于前中后序的非递归遍历,我们需要转变思路:应当将一棵二叉树看成两部分:左路节点、左路节点的右子树
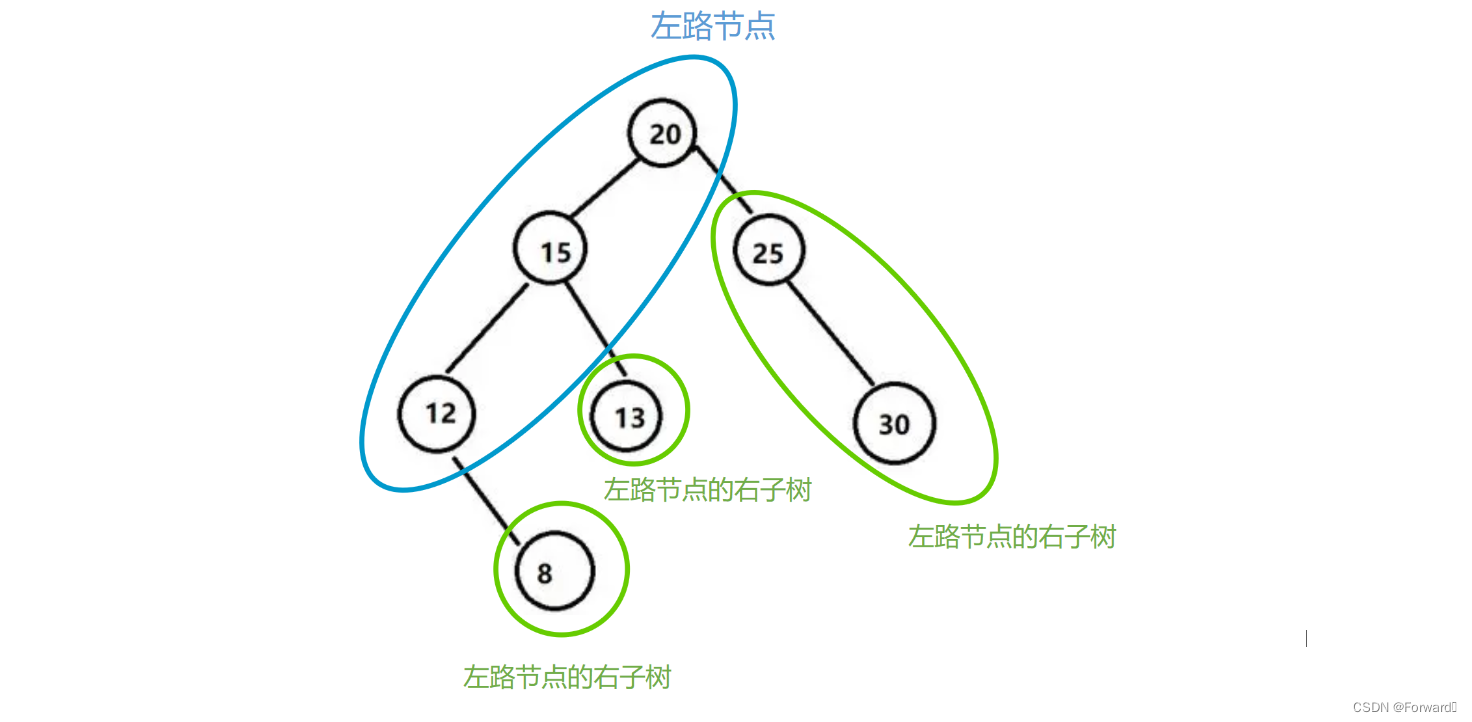
2.1 前序非递归
前序遍历的顺序是:根 -> 左子树 -> 右子树。
具体到一棵二叉树,就是自顶向下将左路节点遍历完,再自底向上遍历左路节点的右子树。如图:
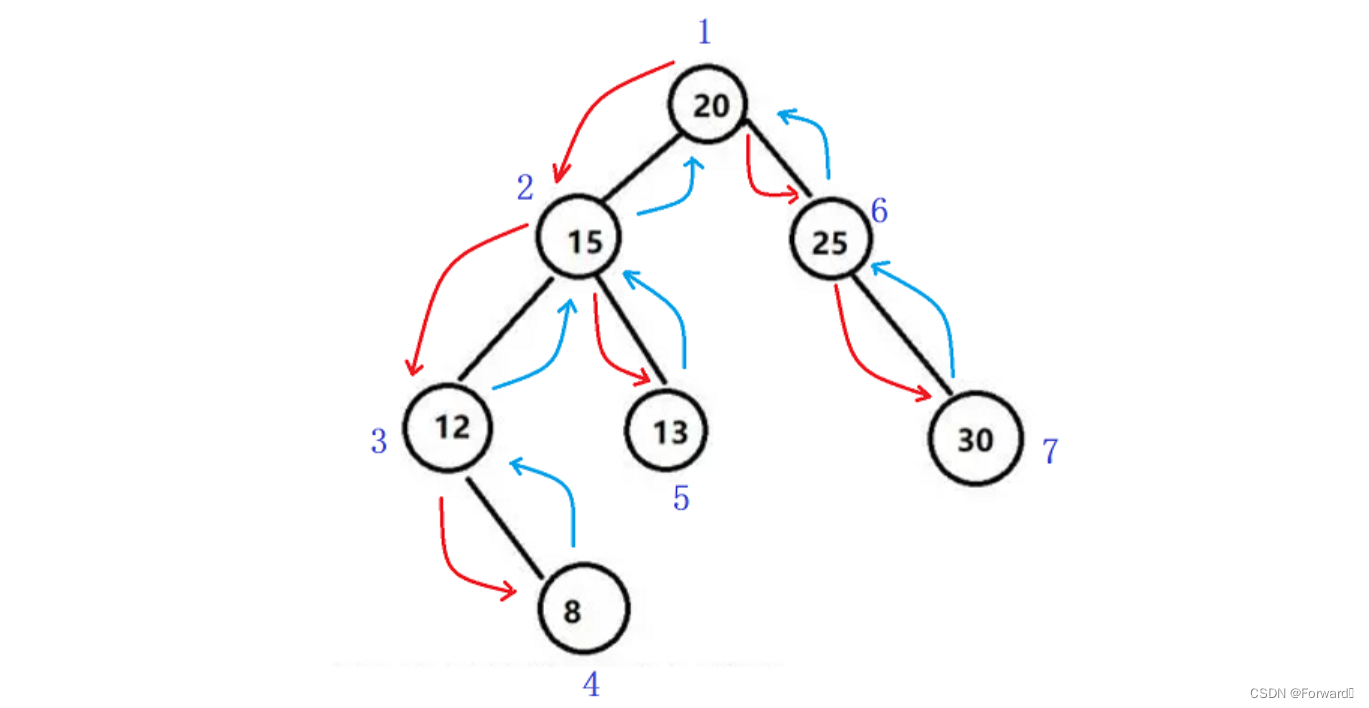
为了能够在遍历完左路节点后还能得到这个节点从而得到这个节点的右子树,我们需要利用栈来对左路节点进行存储。
实现代码:
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> ret;stack<TreeNode*> st;TreeNode* cur = root;while (cur || !st.empty()){//遍历左路节点,将左路节点的值打印的同时将节点入栈while (cur){ret.push_back(cur->val);st.push(cur);cur = cur->left;}TreeNode* tmp = st.top();st.pop();//此时cur即为左路节点的右子树//将这棵右子树看成一颗完整的二叉树,进行相同的操作cur = tmp->right;}return ret;}
};
2.2 中序非递归
中序遍历的顺序是:左子树 -> 根 -> 右子树
具体到一棵二叉树,即从左路节点的最深处开始,先遍历这个节点,再遍历这个节点的右子树,自底向上。
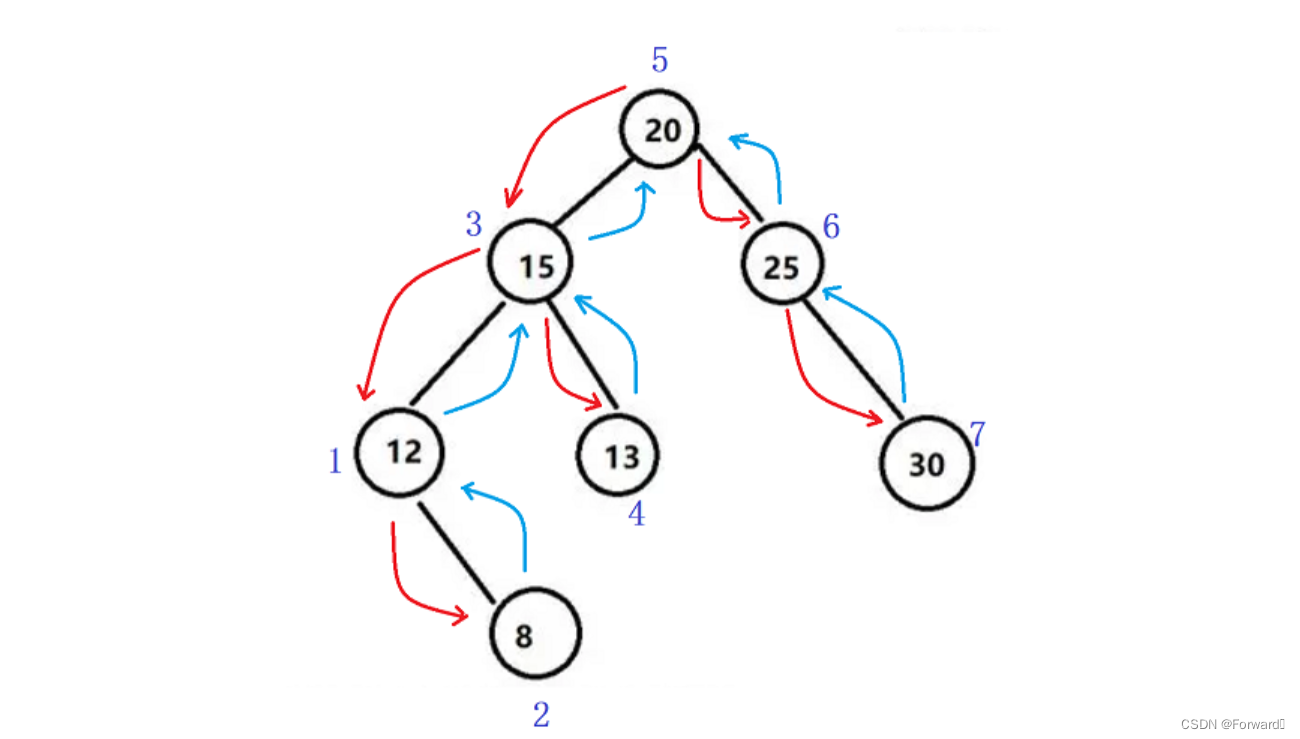
同样,为了能够找到之前的左路节点,也需要一个栈来对左路节点进行保存
实现代码:
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> ret;stack<TreeNode*> st;TreeNode* cur = root;while (cur || !st.empty()){//遍历左路节点的时候将左路节点入栈//由于左子树先于根,因此先不要打印左路节点(根)的值while (cur){st.push(cur);cur = cur->left;}//程序第一次走到这里时,tmp就是左路节点的最深处//tmp的左子树为nullptr(或已经遍历完tmp的左子树),因此打印其(根)值TreeNode* tmp = st.top();st.pop();ret.push_back(tmp->val);//遍历左路节点的右子树cur = tmp->right;}return ret;}
};
2.3 后序非递归
后序的遍历顺序为:左子树 -> 右子树 -> 根
具体到一棵二叉树,即从左路节点的最深处开始,先遍历左路节点的右子树,再遍历左路节点,自底向上。如图:
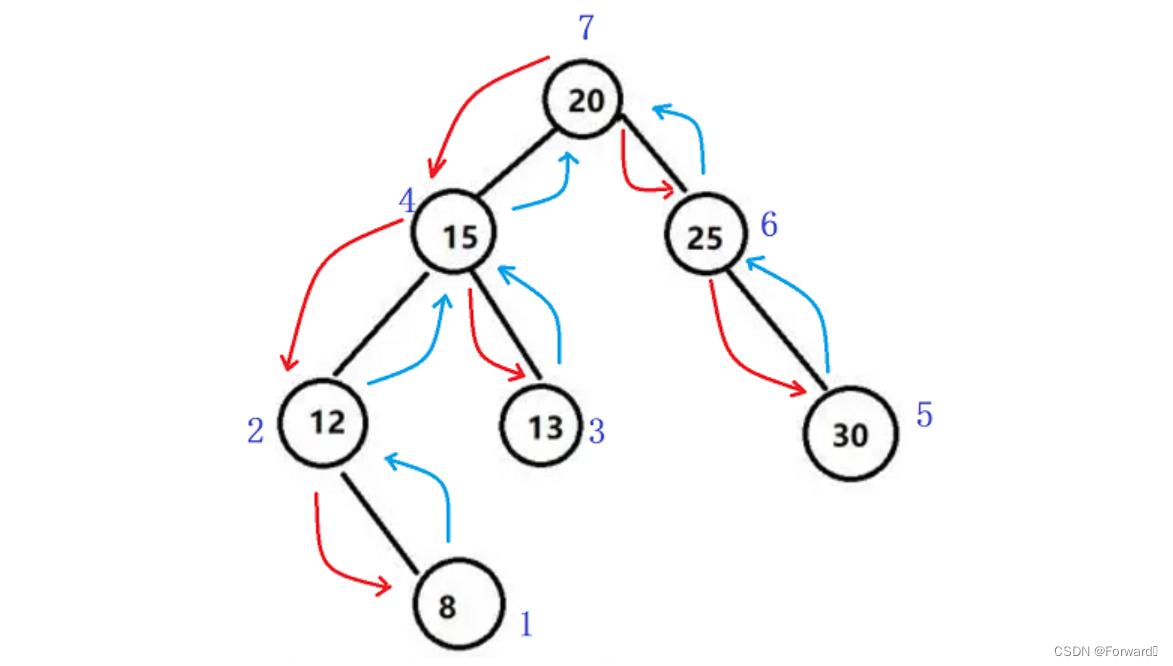
同样,也需要一个栈来保存之前的左路节点
此外,由于后序遍历的顺序为:左子树 -> 右子树 -> 根,需要遍历完根(左路节点)的左子树和右子树后才能对其值进行打印,在这个过程中,我们会经过两次根,且只能在第二次经过根时才能打印根的值,为了确保我们打印根的时机,可以利用一个指针prev来记录之前遍历的位置:如果prev停留在左路节点的右子树的根节点,就说明此时左右子树已经遍历完,可以打印根的值
实现代码:
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> ret;stack<TreeNode*> st;TreeNode* cur = root;TreeNode* prev = nullptr;while (cur || !st.empty()){//将左路节点入栈while (cur){st.push(cur);cur = cur->left;}TreeNode* tmp = st.top();//如果左路节点的右子树为空或者prev停留在右子树的根//说明根的左子树和右子树都已遍历完//打印根值(遍历根),同时跟新prev的位置if (tmp->right == nullptr || prev == tmp->right){ret.push_back(tmp->val);st.pop();prev = tmp;}else //否则,说明根的右子树没有遍历完,遍历右子树cur = tmp->right;}return ret;}
};
2. 二叉树的层序遍历
-
层序遍历又叫广度优先遍历。
-
设二叉树的根节点所在层数为1,层序遍历就是从根节点出发,首先访问第一层的节点,然后从左到右访问第二层上的节点,接着访问第三层的节点,以此类推,自上而下,自左往右逐层访问树的结点的过程就是层序遍历。
-
层序遍历借助队列的先进先出思想来实现。
-
核心思想:上一层带下一层
-
如图就是对上面那棵树的层序遍历示意图:

-
实现代码
typedef BTNode* QDataType; //队列元素类型
typedef struct QueueNode
{struct QueueNode* next;QDataType data;
}QueueNode;
typedef struct Queue //定义存放指向队头,队尾指针的结构体
{QueueNode* head; //指向队头QueueNode* tail; //指向队尾
}Queue;//层序遍历
void LevelOrder(BTNode* root)
{Queue *q = (Queue *)malloc(sizeof(Queue)); //创建队列QueueInit(q); //初始化队列//如果根节点为空,直接退出函数if (!root)return;QueuePush(q, root); //先将根节点入队入队while (!QueueEmpty(q)) //当队列不为空{BTNode* front = QueueFront(q); //接收队头元素QueuePop(q); //出队头元素printf("%c ", front->data); //访问该节点if (front->left) //如果左子树不为空QueuePush(q, front->left); //左子树入队if (front->right) //如果右子树不为空QueuePush(q, front->right); //右子树入队}printf("\n");QueueDestroy(q); //销毁队列
}
3. 二叉树遍历的应用

- 由二叉树和层序遍历的思想,我们可以构造出这棵树
- 再有前序遍历 根- > 左子树 -> 右子树 的思想,可以知道,这棵树的前序序列为:A B D H E C F G

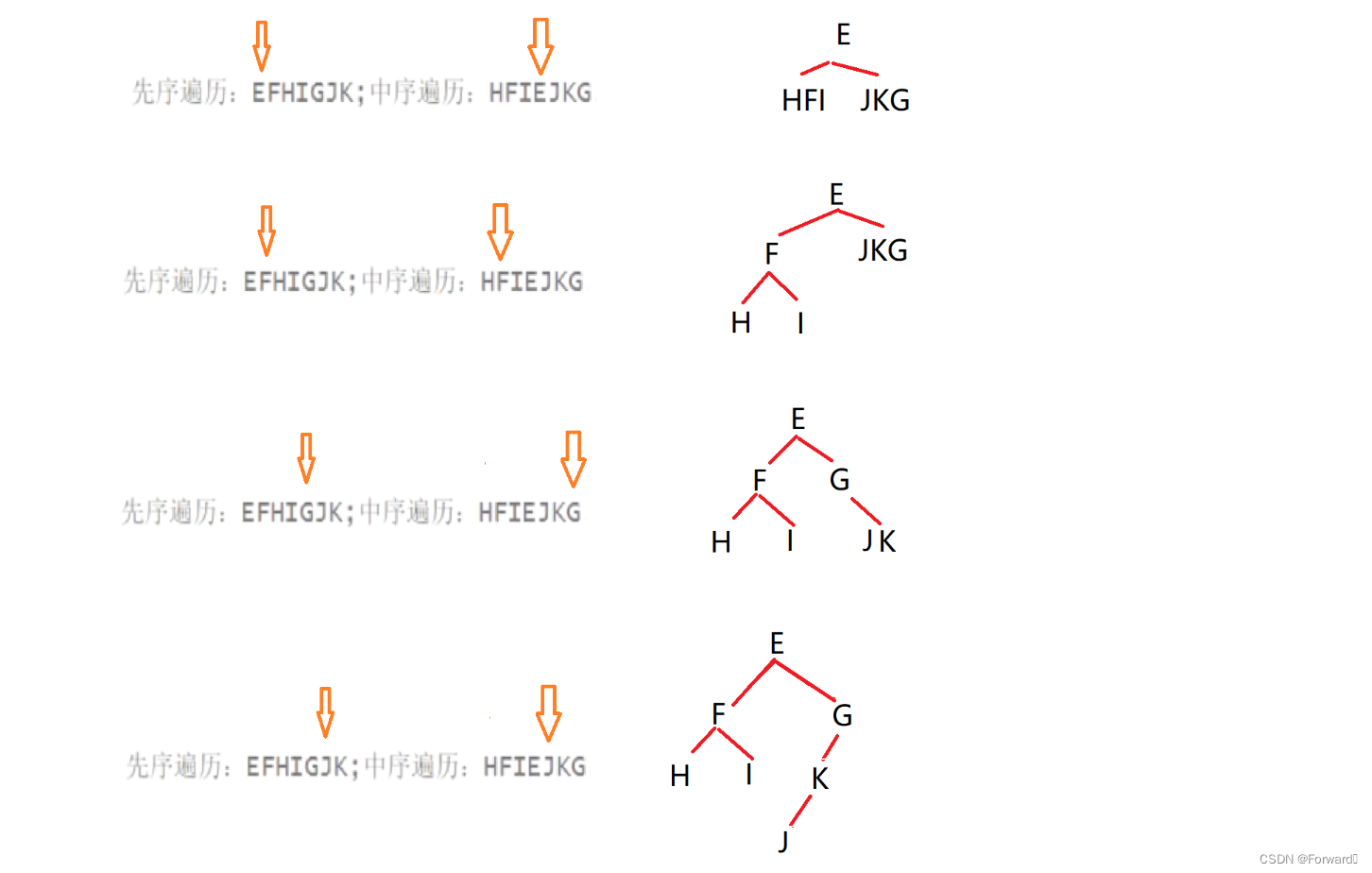
- 这道题是由二叉树的前序序列和中序序列来确定二叉树,我们知道中序遍历的思想是 左子树 -> 根 -> 右子树 ,根将左子树和右子树分割开来,那么我们就可以先用前序序列确定根,再用中序序列确定根的左右子树,这样就可以将这棵二叉树确定了,如图:
- 显然根节点为E
我们同样可以用代码,利用一棵二叉树的前序序列和中序序列来将这棵二叉树还原👉Leetcode -> 从前序与中序遍历序列构造二叉树
class Solution { public://前序序列即为根序列//在中序序列找到根后可以将序列分为左右两部分,这两部分分别就是跟的左子树序列和右子树序列TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder, int& prei, int inBegin, int inEnd){//区间长度小于1,直接返回空if (inBegin > inEnd)return nullptr;//前序序列即为根序列TreeNode* root = new TreeNode(preorder[prei++]);//在中序序列中找到根int pos = 0;while (1){if (root->val != inorder[pos])pos++;elsebreak;}//分别前往左子树和右子树进行连接root->left = _buildTree(preorder, inorder, prei, inBegin, pos - 1);root->right = _buildTree(preorder, inorder, prei, pos + 1, inEnd);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int i = 0;TreeNode* root = _buildTree(preorder, inorder, i, 0, inorder.size() - 1);return root;} };

- 这题和第二题类似,同样是先由后序遍历(左子树 -> 右子树 -> 根)确定根节点,再由中序遍历确定根的左右子树,只是用后序遍历确定根节点时要从最后开始。如图:
易得前序遍历为a b c d e
我们同样可以用代码,利用一棵二叉树的前序序列和中序序列来将这棵二叉树还原👉Leetcode -> 从中序与后序遍历序列构造二叉树
class Solution { public://思想同前序序列和中序序列确定二叉树类似TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder, int& posi, int inBegin, int inEnd){if (inBegin > inEnd)return nullptr;TreeNode* root = new TreeNode(postorder[posi--]);int pos = 0;while (1){if (root->val != inorder[pos])pos++;elsebreak;}root->right = _buildTree(inorder, postorder, posi, pos + 1, inEnd);root->left = _buildTree(inorder, postorder, posi, inBegin, pos - 1);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int i = postorder.size() - 1;TreeNode* root = _buildTree(inorder, postorder, i, 0, inorder.size() - 1);return root;} };
总结:
由于二叉树的中序遍历可以分割二叉树的左右节点,因此 前序序列 + 中序序列 / 后序序列 + 中序序列 都可以构建出一棵二叉树,而单独序列和 前序序列 + 后序序列就不行。
相关文章:

二叉树遍历(前中后序的递归/非递归遍历、层序遍历)
二叉树的遍历 1. 二叉树的前序、中序、后序遍历 前、中、后序遍历又叫深度优先遍历 注:严格来说,深度优先遍历是先访问当前节点再继续递归访问,因此,只有前序遍历是严格意义上的深度优先遍历 首先需要知道下面几点: …...
UE4升级UE5 蓝图节点变更汇总(4.26/27-5.2/5.3)
一、删除部分 Ploygon Editing删除 Polygon Editing这个在4.26、4.27中的插件,在5.1后彻底失效。 相关的蓝图,如编辑器蓝图 Generate mapping UVs等,均失效。 如需相关功能,请改成Dynamic Mesh下的方法。 GetSupportedClass删…...
【python】异常处理
前言 省略各种废话,直接快速整理知识点 try-except 基础 作用 程序不可能永远都是对的,当7除a,a由用户输入时,用户输入0就会报错。try-except就是解决这些问题。 结构 多分支自定义错误类型 上方的exception是一个错误类型…...

【xv6操作系统】Lab systems calls
一、实验前须知 阅读 xv6 文档的第 2 章和第 4 章的 4.3 节和 4.4 节以及相关源文件: 系统调用的用户空间代码在 user/user.h 和 user/usys.pl 中。 内核空间代码在 kernel/syscall.h 和 kernel/syscall.c 中。 与进程相关的代码在 kernel/proc.h 和 kernel/proc.c…...

python的scripts文件夹作用
Windows系统: Scripts文件夹通常位于Python的安装目录下,如C:\Python\Scripts。该文件夹内包含了各种有用的工具,例如pip、virtualenv等,这些工具有助于管理和配置Python环境和依赖包。 Linux系统: 在Linux系统中&…...

Discuz论坛网站报错Discuz!Database Error(0)notconnect的解决办法
运营服务器大本营有段时间了,在运营期间遇到两次Discuz!Database Error(0)notconnect报错,和你们分享遇到Discuz报错的解决办法,希望可以帮助到你。 首先网站报错(0)notconnect&…...

掌握mysql,看完这篇文章就够了
数据库 对大量数据进行存储和管理(增删改查) 客户端: 黑窗口终端navicat 熊掌软件数据库分类: 关系型数据库 通过表与表产生关联关系,每个表中都存储结构化数据,支持sql结构化查询语言MysqlOracleSQLS…...

守护Web安全:了解Web攻击与防护策略
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...

变换,动画
面试题——需求:在不知道父元素与子元素的宽高时 如何让子元素在父元素内居中? 1.定位 父相子绝 2.子元素 top:50% left:50% 3.子元素 transform: translate(-50%,-50%) .parent{height: 500px;background-color: red;position: relative;}.c…...
深度解析速卖通商品详情API:Python实战与高级技术探讨
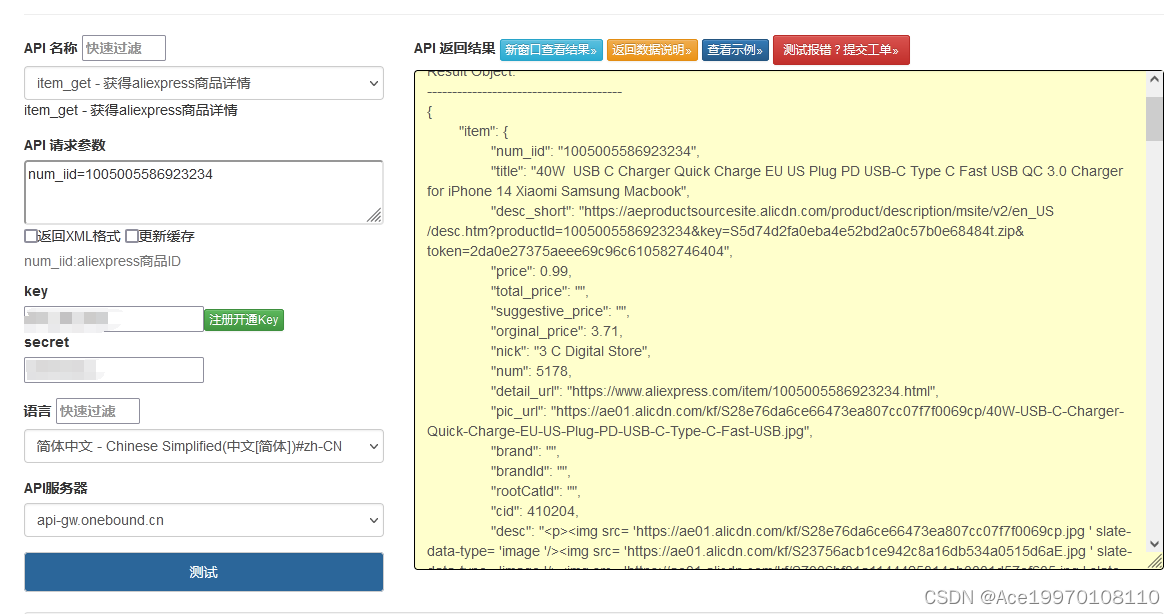
速卖通商品详情API接口实战:Python代码示例 一、准备工作 在开始之前,请确保你已经完成了以下步骤: 在速卖通开放平台注册账号并创建应用,获取API密钥。阅读速卖通商品详情API接口的文档,了解接口的使用方法和参数要…...

背包问题算法
背包问题算法 0-1背包问题二维数组一维数组 完全背包问题二维数组一维数组 多重背包问题一维数组 0-1背包问题 问题:背包的容量为9,有重量分别为[2, 4, 6, 9]的四个物品,价值分别为[3, 4, 5, 6],求背包能装的物品的最大价值是多少…...
echarts柱状图可鼠标左击出现自定义弹框,右击隐藏弹框并阻止默认右击事件
每项x轴数据对应有两条柱图和一条阴影效果是学习其它博客得到的效果,这个是学习的原文链接:echarts两个合并柱体(普通柱状图象形柱图)共享一个柱体阴影 因为这次情况比较特殊,不仅需要自定义弹框内容,而且…...
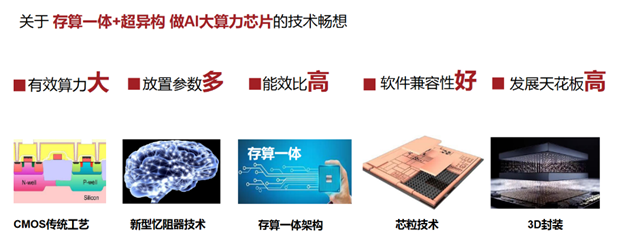
存算一体成为突破算力瓶颈的关键技术?
大模型的训练和推理需要高性能的算力支持。以ChatGPT为例,据估算,在训练方面,1746亿参数的GPT-3模型大约需要375-625台8卡DGX A100服务器训练10天左右,对应A100 GPU数量约3000-5000张。 在推理方面,如果以A100 GPU单卡…...

Pytorch_1_基本语法
一、Pytorch的基本元素操作 1.引入torch from __future__ import print_function import torch 2.创建矩阵 x torch.empty(5,3) print(x) 3.输出结果: tensor([[7.9191e34, 1.1259e24, 1.2359e-42], [4.0824e-40, 1.1379e-35, 2.5353e30], [8.…...

2024上海国际玻璃纤维及新材料展览会
2024上海国际玻璃纤维及新材料展览会 时间:2024年12月18~20日 地点:上海新国际博览中心 ◆ 》》》展会概况: 玻璃纤维是一种性能优异的无机非金属材料,比有机纤维耐温高,不燃,抗腐ÿ…...

云计算项目九:K8S安装
K8S安装 Kube-master安装 按照如下配置准备云主机 防火墙相关配置:禁用selinux,禁用swap,且在firewalld-*。上传kubernetes.zip 到跳板机 配置yum仓库(跳板机) 跳板机主机配置k8s软件源服务端 [rootjs ~]# yum -y…...
sign加密方法生成
1. 引入包的问题 2. 原因 .pycrypto、pycrytodome和crypto是一个东西,crypto在python上面的名字是pycrypto,它是一个第三方库,但是已经停止更新 3. 解决方法 --直接安装:pip install pycryptodome 3.但是,在使用的时…...

【Linux】编译器-gcc/g++使用
个人主页 : zxctscl 文章封面来自:艺术家–贤海林 如有转载请先通知 文章目录 1. 前言2. 初见gcc和g3. 程序的翻译过程3.1 预处理3.1.1 宏替换 去注释 头文件展开3.1.2 条件编译 3.2 编译3.3 汇编3.4 链接 4. 链接4.1 动态链接4.2 静态链接 1. 前言 在之…...
 函数:筛选可迭代对象元素)
Python 中的 filter() 函数:筛选可迭代对象元素
在 Python 中,filter() 函数是一个非常有用的内置函数,用于根据指定条件过滤可迭代对象中的元素。本文将深入探讨 filter() 函数的用法、工作原理以及常见应用场景,以帮助大家更好地理解和运用这个函数。 什么是 filter() 函数? …...

Java高频面试之并发篇
有需要互关的小伙伴,关注一下,有关必回关,争取今年认证早日拿到博客专家 并行和并发有什么区别? 并行是同时执行多个任务,而并发是多个任务在一段时间内交替执行。并行(Parallel)是指同时执行多个任务或操作,通过同时…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...