指数移动平均(EMA)
文章目录
- 前言
- EMA的定义
- 在深度学习中的应用
- PyTorch代码实现
- yolov5中模型的EMA实现
- 参考
前言
在深度学习中,经常会使用EMA(指数移动平均)这个方法对模型的参数做平均,以求提高测试指标并增加模型鲁棒。
实际上,_EMA可以看作是Temporal Ensembling,在模型学习过程中融合更多的历史状态,从而达到更好的优化效果。
EMA的定义
指数移动平均(Exponential Moving Average)也叫权重移动平均(Weighted Moving Average),是一种给予近期数据更高权重的平均方法。
假设有n个权重数据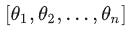 :
:
- 普通的平均数:
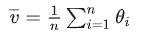
- EMA:
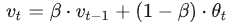
其中, vt表示前 t条的平均值 ( v0=0 ),β是加权权重值 (一般设为0.9-0.999)。
Andrew Ng在Course 2 Improving Deep Neural Networks中讲到,EMA可以近似看成过去 1/(1−β) 个时刻 v 值的平均。
普通的过去n时刻的平均是这样的: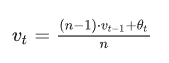
类比EMA,可以发现当 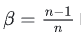 时,两式形式上相等。需要注意的是,两个平均并不是严格相等的,这里只是为了帮助理解。
时,两式形式上相等。需要注意的是,两个平均并不是严格相等的,这里只是为了帮助理解。
实际上,EMA计算时,过去 1/(1−β) 个时刻之前的数值平均会decay到 1/e 的加权比例,证明如下。
如果将这里的 vt展开,可以得到: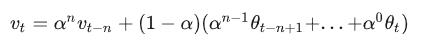
其中, 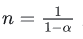 ,代入可以得到
,代入可以得到 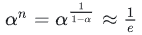 。
。
在深度学习中的应用
上面讲的是广义的ema定义和计算方法,特别的,在深度学习的优化过程中, 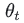 是t时刻的模型权重weights, vt是t时刻的影子权重(shadow weights)。在梯度下降的过程中,会一直维护着这个影子权重,但是这个影子权重并不会参与训练。
是t时刻的模型权重weights, vt是t时刻的影子权重(shadow weights)。在梯度下降的过程中,会一直维护着这个影子权重,但是这个影子权重并不会参与训练。
基本的假设是,模型权重在最后的n步内,会在实际的最优点处抖动,所以我们取最后n步的平均,能使得模型更加的鲁棒。
PyTorch代码实现
下面是一个简单的指数移动平均(EMA)的PyTorch实现:
import torchclass EMA():def __init__(self, alpha):self.alpha = alpha # 初始化平滑因子alphaself.average = None # 初始化平均值为空self.count = 0 # 初始化计数器为0def update(self, x):if self.average is None: # 如果平均值为空,则将其初始化为与x相同大小的全零张量self.average = torch.zeros_like(x)self.average = self.alpha * x + (1 - self.alpha) * self.average # 更新平均值self.count += 1 # 更新计数器def get(self):return self.average / (1 - self.alpha ** self.count) # 根据计数器和平滑因子计算EMA值,并返回平均值除以衰减系数的结果在这个类中,我们定义了三个方法,分别是__init__、update和get。
- __init__方法用于初始化平滑因子alpha、平均值average和计数器count
- update方法用于更新EMA值
- get方法用于获取最终的EMA值。
使用这个类时,我们可以先实例化一个EMA对象,然后在每个时间步中调用update方法来更新EMA值,最后调用get方法来获取最终的EMA值。
例如:
ema = EMA(alpha=0.5)
for value in data:ema.update(torch.tensor(value))
smoothed_data = ema.get()
在这个例子中,我们使用alpha=0.5来初始化EMA对象,然后遍历数据集data中的每个数据点,调用update方法更新EMA值。最后我们调用get方法来获取平滑后的数据。
yolov5中模型的EMA实现
如下:
class ModelEMA:""" Updated Exponential Moving Average (EMA) from https://github.com/rwightman/pytorch-image-modelsKeeps a moving average of everything in the model state_dict (parameters and buffers)For EMA details see https://www.tensorflow.org/api_docs/python/tf/train/ExponentialMovingAverage"""def __init__(self, model, decay=0.9999, tau=2000, updates=0):# Create EMAself.ema = deepcopy(de_parallel(model)).eval() # FP32 EMAself.updates = updates # number of EMA updatesself.decay = lambda x: decay * (1 - math.exp(-x / tau)) # decay exponential ramp (to help early epochs)for p in self.ema.parameters():p.requires_grad_(False)def update(self, model):# Update EMA parametersself.updates += 1d = self.decay(self.updates)msd = de_parallel(model).state_dict() # model state_dictfor k, v in self.ema.state_dict().items():if v.dtype.is_floating_point: # true for FP16 and FP32v *= dv += (1 - d) * msd[k].detach()# assert v.dtype == msd[k].dtype == torch.float32, f'{k}: EMA {v.dtype} and model {msd[k].dtype} must be FP32'def update_attr(self, model, include=(), exclude=('process_group', 'reducer')):# Update EMA attributescopy_attr(self.ema, model, include, exclude)参考
https://zhuanlan.zhihu.com/p/68748778
如果有用,请点个三连呗 点赞、关注、收藏。
你的鼓励是我最大的动力
相关文章:
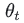
指数移动平均(EMA)
文章目录 前言EMA的定义在深度学习中的应用PyTorch代码实现yolov5中模型的EMA实现 参考 前言 在深度学习中,经常会使用EMA(指数移动平均)这个方法对模型的参数做平均,以求提高测试指标并增加模型鲁棒。实际上,_EMA可以…...

无线表格识别模型LORE转换库:ConvertLOREToONNX
引言 总有小伙伴问到阿里的无线表格识别模型是如何转换为ONNX格式的。这个说来有些惭愧,现有的ONNX模型是很久之前转换的了,转换环境已经丢失,且没有做任何笔记。 今天下定决心再次尝试转换,庆幸的是转换成功了。于是有了转换笔…...
C# 视频转图片
在 C# 中将视频转换为图像可以使用 FFmpeg 库。下面是一个示例代码来完成这个任务: using System; using System.Diagnostics;class Program {static void Main(string[] args){string inputFile "input_video.mp4"; // 输入的视频文件路径string outpu…...
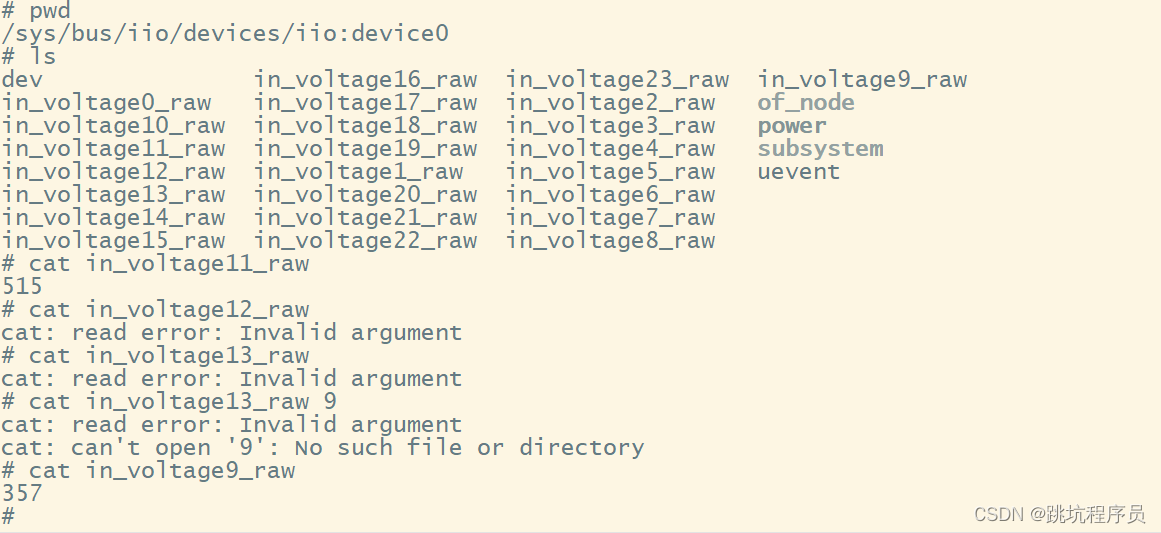
LINUX ADC使用
监测 ADC ,使用CAT 查看: LINUX ADC基本使用 &adc {pinctrl-names "default";pinctrl-0 <&adc6>;pinctrl-1 <&adc7>;pinctrl-2 <&adc8>;pinctrl-3 <&adc9>;pinctrl-4 <&adc10>;pinctrl-5 …...

Ubuntu 基本操作-嵌入式 Linux 入门
在 Ubuntu 基本操作 里面基本就分为两部分: 安装 VMware 运行 Ubuntu熟悉 Ubuntu 的各种操作、命令 如果你对 Ubuntu 比较熟悉的话,安装完 VMware 运行 Ubuntu 之后就可以来学习下一章节了。 1. 安装 VMware 运行 Ubuntu 我们首先来看看怎么去安装 V…...

Pytorch可形变卷积分类模型与可视化
E:. │ archs.py │ dataset.py │ deform_conv_v2.py │ train.py │ utils.py │ visual_net.py │ ├─grad_cam │ 2.png │ 3.png │ ├─image │ ├─1 │ │ 154.png │ │ 2.png │ │ │ ├─2 │ │ 143.png │…...

Mysql 表逻辑分区原理和应用
MySQL的表逻辑分区是一种数据库设计技术,它允许将一个表的数据分布在多个物理分区中,但在逻辑上仍然表现为一个单一的表。这种方式可以提高查询性能、简化数据管理,并有助于高效地进行大数据量的存储和访问。逻辑分区基于特定的规则ÿ…...

架构面试题汇总:网络协议34问(七)
码到三十五 : 个人主页 心中有诗画,指尖舞代码,目光览世界,步履越千山,人间尽值得 ! 网络协议是实现各种设备和应用程序之间顺畅通信的基石。无论是构建分布式系统、开发Web应用,还是进行网络通信&#x…...

lida,一个超级厉害的 Python 库!
目录 前言 什么是 lida 库? lida 库的安装 基本功能 1. 文本分词 2. 词性标注 3. 命名实体识别 高级功能 1. 情感分析 2. 关键词提取 实际应用场景 1. 文本分类 2. 情感分析 3. 实体识别 总结 前言 大家好,今天为大家分享一个超级厉害的 Python …...

K好数 C语言 蓝桥杯算法提升ALGO3 一个自然数N的K进制表示中任意的相邻的两位都不是相邻的数字
问题描述 如果一个自然数N的K进制表示中任意的相邻的两位都不是相邻的数字,那么我们就说这个数是K好数。求L位K进制数中K好数的数目。例如K 4,L 2的时候,所有K好数为11、13、20、22、30、31、33 共7个。由于这个数目很大,请你输…...
2195. 深海机器人问题(网络流,费用流,上下界可行流,网格图模型)
活动 - AcWing 深海资源考察探险队的潜艇将到达深海的海底进行科学考察。 潜艇内有多个深海机器人。 潜艇到达深海海底后,深海机器人将离开潜艇向预定目标移动。 深海机器人在移动中还必须沿途采集海底生物标本。 沿途生物标本由最先遇到它的深海机器人完成采…...

Vue/cli项目全局css使用
第一步:创建css文件 在合适的位置创建好css文件,文件可以是sass/less/stylus...第二步:响预处理器loader传递选项 //摘自官网,引入样式 // vue.config.js module.exports {css: {loaderOptions: {// 给 sass-loader 传递选项sa…...
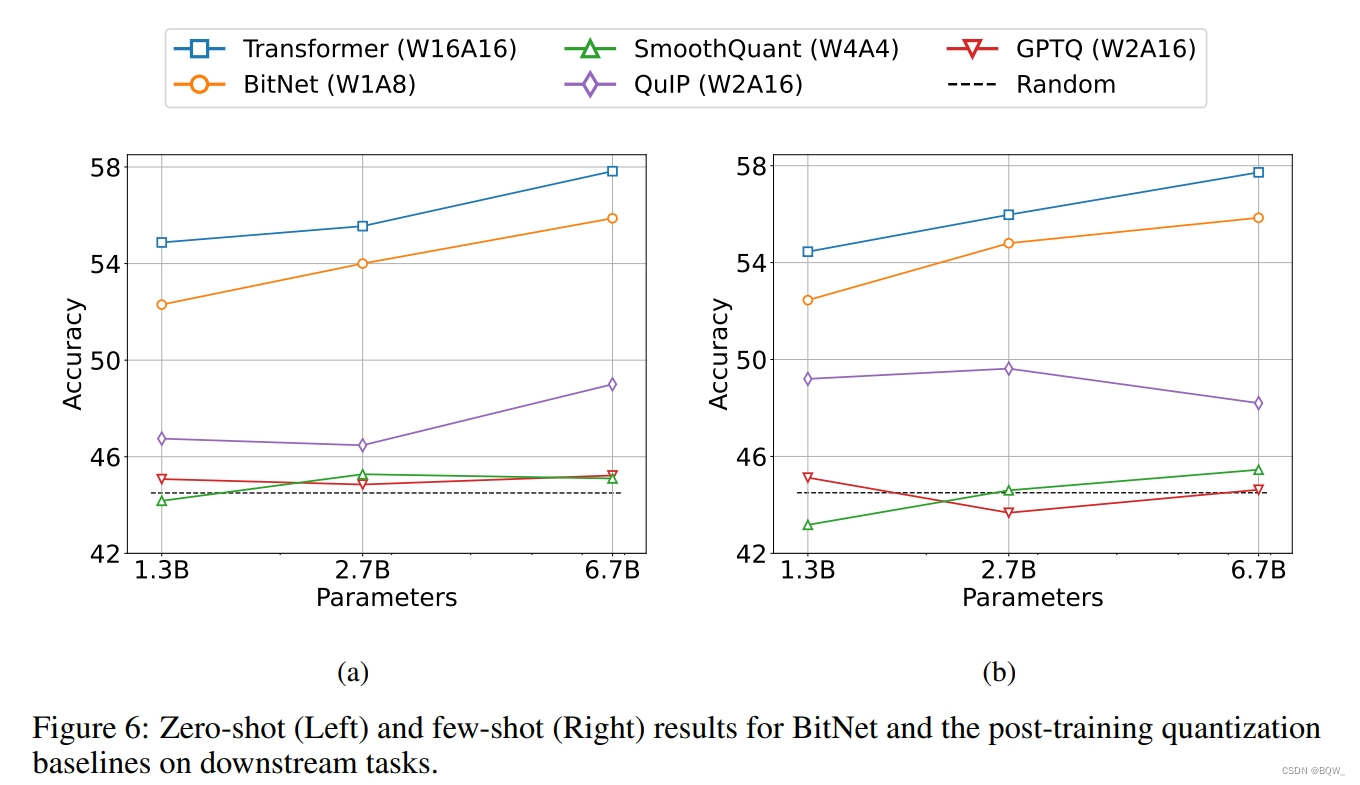
【自然语言处理】【大模型】BitNet:用1-bit Transformer训练LLM
BitNet:用1-bit Transformer训练LLM 《BitNet: Scaling 1-bit Transformers for Large Language Models》 论文地址:https://arxiv.org/pdf/2310.11453.pdf 相关博客 【自然语言处理】【大模型】BitNet:用1-bit Transformer训练LLM 【自然语言…...
安装及管理docker
文章目录 1.Docker介绍2.Docker安装3.免sudo设置4. 使用docker命令5.Images6.运行docker容器7. 管理docker容器8.创建image9.Push Image 1.Docker介绍 Docker 是一个简化在容器中管理应用程序进程的应用程序。容器让你在资源隔离的进程中运行你的应用程序。类似于虚拟机&#…...
【MySQL】表的增删改查——MySQL基本查询、数据库表的创建、表的读取、表的更新、表的删除
文章目录 MySQL表的增删查改1. Create(创建)1.1 单行插入1.2 多行插入1.3 替换 2. Retrieve(读取)2.1 select查看2.2 where条件2.3 结果排序2.4 筛选分页结果 3. Update(更新)3.1 更新单个数据3.2 更新多个…...

C/C++蓝桥杯之日期问题
问题描述:小明正在整理一批文献,这些文献中出现了很多日期,小明知道这些日期都在1960年1月1日至2059年12月31日之间,令小明头疼的是,这些日期采用的格式非常不统一,有采用年/月/日的,有采用月/日…...

【理解指针(二)】
文章目录 一、指针的运算(1)指针加整数(2)指针减指针(指针关系运算) 二、野指针(1)野指针的成因(1.1)指针未初始化(1.2)指针的越界访问…...

使用AI纠正文章
我写了一段关于哲学自学的读书笔记,处于好奇的目的,让AI帮我纠正语法和逻辑。我的原文如下: 泰勒斯第一次提出了水是万物本源的说法,对于泰勒斯为什么提出这样的观点,或者是这样的观点是怎么来的,我们无从所…...

拼多多API批量获取商品详情信息
随着电子商务的蓬勃发展,淘宝作为中国最大的在线购物平台之一,每天需要处理海量的商品上架和交易。为了提高工作效率,自动化上架商品和批量获取商品详情信息成为了许多商家和开发者的迫切需求。本文将详细介绍淘宝的API接口及其相关技术&…...
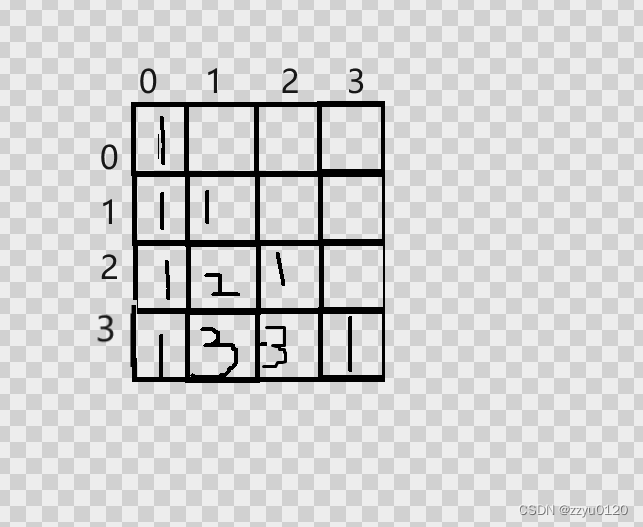
杨辉三角(C语言)
杨辉三角 一.什么是杨辉三角 一.什么是杨辉三角 每个数等于它上方两数之和。 每行数字左右对称,由1开始逐渐变大。 第n行的数字有n项。 前n行共[(1n)n]/2 个数。 … 当前行的数上一行的数上一行的前一列的数 void yanghuisanjian(int arr[][20], int n) {for (int i…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...
