C语言:深入补码计算原理
C语言:深入补码计算原理
- 有符号整数存储
- 原码、反码、补码
- 转换规则
- 数据与内存的关系
- 补码原理
有符号整数存储
原码、反码、补码
有符号整数的2进制表示方法有三种,即原码、反码和补码
三种表示方法均有符号位和数值位两部分,符号位用0表示“正”,用1表示“负”。
有符号整数最高位的一位是被当做符号位,剩余的都是数值位。
无符号整数所有的位都是数值位
转换规则
正整数:原、反、补码都相同。
负整数:
原码:直接将数值按照正负数的形式翻译成二进制得到的就是原码。
反码:将原码的符号位不变,其他位依次按位取反就可以得到反码。
补码:反码+1就得到补码。
正数:
int a = 5;
对于int(整形),内存会开辟4个字节来存放a。由于a是正数,第一位符号位为0,数值为5,转化为二进制就是101,高位补0。正数的原反补三码相同。
故:
a 的原码:
00000000 00000000 00000000 00000101
a 的反码:00000000 00000000 00000000 00000101
a 的补码:00000000 00000000 00000000 00000101
负数:
int b = -5;
由于在此b是负数,在原码中,第一位是符号位,存放1,表示负数。
反码:符号位不变,保持为1。其余位按位取反,即0变1,1变0.
补码:在反码的情况下加1。
故:
b 的原码:
10000000 00000000 00000000 00000101
b 的反码:11111111 11111111 11111111 11111010
b 的补码:11111111 11111111 11111111 11111011
而补码想要变回原码,也是相同的步骤,即先取反后加一。
数据与内存的关系
首先,我们在内存中存储的数据是以补码的形式存储的。我们用代码定义a,b为5和-5,然后观察其在内存中的值:
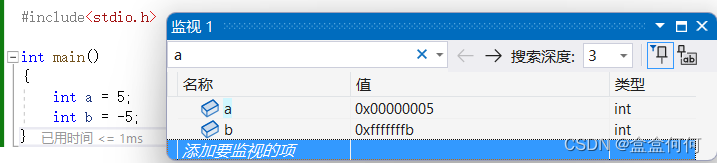
由于二进制实在难于分辨,可读性非常差,所以编译器在向程序员呈现计算机存储的值的时候,会转为16进制。我们从上图中可见,a的存储是0x00000005即16进制的5。可b的值却不是-00000005。这个fffffffb其实就是-5的补码 11111111 11111111 11111111 11111011的16进制形式,由此可以证明,内存存储有符号整数就是以补码的形式。
那为什么内存要存补码?
- 可以把符号与数值统一处理,把数字的正负放在码值中,不用额外区分。
- 可以使加法减法统一处理(CPU只有加法计算器)。
第一点其实是容易理解的,那为什么用补码可以统一加减法呢?我们以下面的代码为例:
int a = 3;
int b = 5;
int c = a - b;
在以上计算过程中,计算机会把3 - 5当作3 + (-5),然后将两个数字的补码相加。
a 的补码:
00000000 00000000 00000000 00000011
b 的补码:11111111 11111111 11111111 11111011
--------------------------------------------
两者相加:11111111 11111111 11111111 11111110
上式取反:10000000 00000000 00000000 00000001
上式加一:10000000 00000000 00000000 00000010
最后得到的值即为-2
可以看到我们确实以加法的形式,完成了减法的计算。以上代码中,计算机想要完成3 - 5,于是CPU将其转化为了3 + (-5),然后直接将补码相加,然后转回原码,得到的就是正确答案。
我们再来看到一个案例:
int a = 10;
int b = 5;
int c = a - b;
在以上计算过程中,计算机会把10 - 5当作10 + (-5),然后将两个数字的补码相加。
a 的补码:
00000000 00000000 00000000 00001010
b 的补码:11111111 11111111 11111111 11111011
--------------------------------------------
两者相加:1 00000000 00000000 00000000 00000101
此时出现了一个问题,那就是进位导致的位数溢出,由于int类型只能存储32位数据,此时超出的数据就会被丢弃。
所以计算后实际值是: 00000000 00000000 00000000 00000101也就是5,我们再次完成了计算。
可见,虽然代码是减法,但是在计算机处理的时候,只做了加法运算。这样可以减少计算机硬件的消耗,只需要在CPU内部做好加法的硬件即可。
本博客还要继续探讨,为什么计算机可以通过补码计算统一加减法。
补码原理
现在假设我们有一个十进制计算机,每个bit位可以存储0 - 9十种数据,现在我们有一个可以存储4位数据内存,接下来我们要完成一个计算:
求出
50 - 19的结果:
值得注意的是:由于我们只能存储4位数据,所以如果我们计算中发生了溢出,多出来的位要舍弃。
50的存储:0050
19的存储:0019
接下来我们进行计算:
50 - 19
=50 + (-19)
=50 + (-19) + 9999 + 1 - 10000
到这一步,我暂时停止了,因为我要重复申明刚刚的规则:计算中发生了溢出,多出来的位要舍弃。
由于计算机只能存储四位,而计算机是一步一步进行计算的,所以中间的每一个变量都要保存下来,而在保存10000时,我们的位数溢出了,要舍弃高位的1,于是上述计算变为:
=
50 + (9999 - 19) + 1 - 0000
=50 + (9999 - 19 + 1)
=50 + 9981
=10031
由于计算机只能存储四位,而在保存10031时,我们的位数溢出了,舍弃高位的1,于是上述计算变为:
=
0031
=31
而50 - 19结果就是31,整个计算过程看起来非常怪异,为什么还能得到正确结果???
首先,我们要计算的是一个减法 50 - 19,于是我把它转化为了加法50 + (-19),但是这依然改变不了它需要进行相减的本质,我们有没有办法把-19转化为一个正数x,让50 + x == 50 + (-19)?
在数学界,这就是异想天开,但是我们的数据是存在计算机中的,其实是有可能实现的,而实现它的本质,就在于丢弃溢出位数的功能。
数学角度,10000 + (-19) + 50等于10031,但是从这个只能存四位的内存的角度,10031就是31。也就是说,我们可以给一个负数加上刚好到溢出位数的数字,故意让其溢出,这样就可以50 + (10000 - 19) == 50 + (-19)了。
但是这涉及到一个问题:根本没有四位的内存可以存下10000这个数据,那就更无法在计算机中完成10000 + (-19)了。于是我们将10000拆分为两个4位以内的数字9999 和 1,让10000 + (-19)变成9999 + 1 + (-19),这就是计算机可以执行的了。这样你也许就可以看懂以上的算式了。
接下来,我们要把上面的溢出效果带入到一般的二进制计算机中:
现在我们要完成减法:5 - 3,数据都以int类型存储:
那么我们就要先将上式转化为5 + (-3),接着对-3进行一次溢出的计算:
-3的二进制:-00000000 00000000 00000000 00000011(前面有负号)
加上一个刚好溢出的整数:1 00000000 00000000 00000000 00000000
拆解出两个int可以存储的数字:11111111 11111111 11111111 11111111+1
先让-3+11111111 11111111 11111111 11111111
结果:11111111 11111111 11111111 11111100
再+1:11111111 11111111 11111111 11111101
最后我们就可以拿11111111 11111111 11111111 11111101 代替-3进行计算了。
而中途有一个过程:
先让
-3+11111111 11111111 11111111 11111111
结果:11111111 11111111 11111111 11111100
你有没有发现,这个结果11111111 11111111 11111111 11111100 刚好就是-3的每一位取反?
数学角度来说,-3 + 11111111 11111111 11111111 11111111 是要执行减法的,可是二进制中可以用每一位取反达到同样的效果,而对于计算机而言,对每一个bit位取反并不是什么难事。因此计算机的计算,就是在这一步把减法消除掉的。
其实这就是得到反码的过程,所以反码要求按位取反!
而最后一步
再+1:
11111111 11111111 11111111 11111101
也就是得到补码的过程:反码 + 1,这是为了补齐前面少的一个数字,凑出刚好溢出的数字。
整个过程都是为了让一个负数转化为一个等效的正数。而之所以要分反码补码,不能一步到位,就是因为刚好差1,内存位数不够无法存储,必须拆一个1出来分两步计算。
另外的,因为有符号整数,既可以存正数,也可以存负数,所以拿出第一位当符号位。而符号位不参与计算,因此取反的时候不包括符号位。
至此,你应该明白了为什么要用补码的机制存储,也就是利用溢出机制,凑出一个等效的正数,然后再计算。
相关文章:

C语言:深入补码计算原理
C语言:深入补码计算原理 有符号整数存储原码、反码、补码转换规则数据与内存的关系 补码原理 有符号整数存储 原码、反码、补码 有符号整数的2进制表示方法有三种,即原码、反码和补码 三种表示方法均有符号位和数值位两部分,符号位用0表示“…...

【Pytorch】新手入门:基于sklearn实现鸢尾花数据集的加载
【Pytorch】新手入门:基于sklearn实现鸢尾花数据集的加载 🌈 个人主页:高斯小哥 🔥 高质量专栏:Matplotlib之旅:零基础精通数据可视化、Python基础【高质量合集】、PyTorch零基础入门教程👈 希望…...
maven项目引入私有jar,并打包到java.jar中
私有jar存放位置 maven依赖 <dependency><groupId>com.hikvision.ga</groupId><artifactId>artemis-http-client</artifactId><version>1.1.10</version><scope>system</scope><systemPath>${project.basedir}/s…...

Django中的Cookie和Session
文章目录 cookie是什么Django中如何使用cookieCookie使用示例session是什么Django中如何使用会话sessionSession使用示例小结 HTTP协议本身是”无状态”的,在一次请求和下一次请求之间没有任何状态保持,服务器无法识别来自同一用户的连续请求。有了cooki…...
)
Git-安装与使用(快速上手图文教程)
Git-安装与使用(快速上手图文教程) - 知乎 克隆: 首先你进去你要存放代码的位置,比如将代码存放到D盘,然后在D盘中右键,点击Git Bash Here,就是说本地仓库要在D盘建立。然后出现git 命令行界面…...
VBA_NZ系列工具NZ02:VBA读取PDF使用说明
我的教程一共九套及VBA汉英手册一部,分为初级、中级、高级三大部分。是对VBA的系统讲解,从简单的入门,到数据库,到字典,到高级的网抓及类的应用。大家在学习的过程中可能会存在困惑,这么多知识点该如何组织…...
所在的位置)
如何在paddlehub库中找到paddlehub.Module()所在的位置
要在PaddleHub库中找到paddlehub.Module()的位置,您可以通过以下步骤在PaddleHub库的源代码中进行查找: 1.确定PaddleHub库的安装位置:首先,确定您安装PaddleHub库的位置。通常,PaddleHub库会被安装在Python的site-pa…...

创建旅游景点图数据库Neo4J技术验证
文章目录 创建旅游景点图数据库Neo4J技术验证写在前面基础数据建库python3源代码KG效果KG入库效率优化方案PostGreSQL建库 创建旅游景点图数据库Neo4J技术验证 写在前面 本章主要实践内容: (1)neo4j知识图谱库建库。使用导航poi中的公园、景…...

Docker一键部署WordPress
使用Docker安装WordPress相对传统安装方式更加便捷高效,因为它可以快速创建一个包含所有必要组件(Web服务器、PHP和MySQL数据库)的独立容器环境。下面是一个简化的步骤说明如何使用Docker和Docker Compose安装WordPress: 一 安装…...
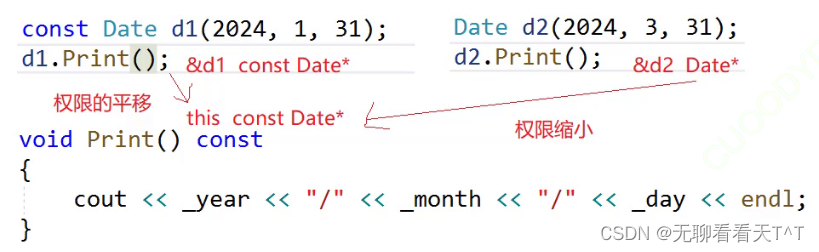
C++的类与对象(五):赋值运算符重载与日期类的实现
目录 比较两个日期对象 运算符重载 赋值运算符重载 连续赋值 日期类的实现 Date.h文件 Date.cpp文件 Test.cpp文件 const成员 取地址及const取地址操作符重载 比较两个日期对象 问题描述:内置类型可直接用运算符比较,自定义类型的对象是多个…...

【uni-app小程序开发】实现一个背景色渐变的滑动条slider
先直接附上背景色渐变的滑动条slider uni-module插件地址:https://ext.dcloud.net.cn/plugin?id16841 最近做的一个用uni-appvue2开发的微信小程序项目中要实现一个滑动进度控制条,如下图所示: 1. 滑动条需要渐变背景色 2. 滑块的背景色需…...

Claude3横空出世:颠覆GPT-4,Anthropic与亚马逊云科技共启AI新时代
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...

【AI视野·今日NLP 自然语言处理论文速览 第八十三期】Wed, 6 Mar 2024
AI视野今日CS.NLP 自然语言处理论文速览 Wed, 6 Mar 2024 Totally 74 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers MAGID: An Automated Pipeline for Generating Synthetic Multi-modal Datasets Authors Hossein Aboutalebi, …...
【AI视野·今日Robot 机器人论文速览 第八十二期】Tue, 5 Mar 2024
AI视野今日CS.Robotics 机器人学论文速览 Tue, 5 Mar 2024 Totally 63 papers 👉上期速览✈更多精彩请移步主页 Interesting: 📚双臂机器人拧瓶盖, (from 伯克利) website: https://toruowo.github.io/bimanual-twist 📚水下抓取器, (from …...

流量分析-webshell管理工具
文章目录 CSCS的工作原理CS流量特征 菜刀phpJSPASP 蚁剑冰蝎哥斯拉 对于常见的webshell管理工具有中国菜刀,蚁剑,冰蝎,哥斯拉。同时还有渗透工具cobaltstrike(CS)。 CS CobaltStrike有控制端,被控端,服务端。(相当于黑…...

备考2025年AMC8数学竞赛:吃透2000-2024年600道AMC8真题就够
我们继续来随机看五道AMC8的真题和解析,根据实践经验,对于想了解或者加AMC8美国数学竞赛的孩子来说,吃透AMC8历年真题是备考最科学、最有效的方法之一。 即使不参加AMC8竞赛,吃透了历年真题600道和背后的知识体系,那么…...
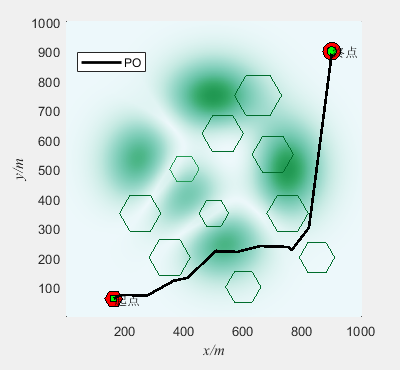
基于鹦鹉优化算法(Parrot optimizer,PO)的无人机三维路径规划(提供MATLAB代码)
一、无人机路径规划模型介绍 无人机三维路径规划是指在三维空间中为无人机规划一条合理的飞行路径,使其能够安全、高效地完成任务。路径规划是无人机自主飞行的关键技术之一,它可以通过算法和模型来确定无人机的航迹,以避开障碍物、优化飞行…...

linux Shell 命令行-02-var 变量
拓展阅读 linux Shell 命令行-00-intro 入门介绍 linux Shell 命令行-02-var 变量 linux Shell 命令行-03-array 数组 linux Shell 命令行-04-operator 操作符 linux Shell 命令行-05-test 验证是否符合条件 linux Shell 命令行-06-flow control 流程控制 linux Shell 命…...

C#MQTT编程10--MQTT项目应用--工业数据上云
1、文章回顾 这个系列文章已经完成了9个内容,由浅入深地分析了MQTT协议的报文结构,并且通过一个有效的案例让伙伴们完全理解理论并应用到实际项目中,这节继续上马一个项目应用,作为本系列的结束,奉献给伙伴们&#x…...

exceljs解析和生成excel文件
安装 npm install exceljs解析excel 通过 Workbook 的 readFile 方法可以拿到workbook对象, workbook对象包含的概念有 worksheet(工作表) --> row(行) --> cell(单元格).于是可以通过依次遍历 worksheet, row, cell来拿到单元格的数据直接通过 worksheet.getSheetValue…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
