C语言数组的维数该如何理解?
一、问题
什么叫做维,维是不是数组中数的个数呢?
二、解答
维数是数组元素的下标个数。使⽤数组的时候,如果只有⼀个下标,则称为⼀维数组,⼀维数组⼀般表示⼀种线性数据的组合。⼆维数组则是有两个下标,可以将其看做是平⾯数据的组合。三维数组有三个下标,可以看做是⽴⽅体。
对现实问题,问题整体可以由⼏个不同⽅⾯去描述,以便区分不同个体。对⼀组考试成绩,如果只由姓名来区分,就是⼀维数组;如果⽤姓名、科⽬来区分就是⼆维数组:⽤姓名、科⽬、考试时间来区分,就是三维数组….C 语⾔对数组下标的数量没有限制。
三、总结
⼀维、⼆维、三维可以表示为⼏何中的直线、平⾯、⽴体。四维及以上的数组没有办法⽤对应的⼏何⽅式描述。
相关文章:

C语言数组的维数该如何理解?
一、问题 什么叫做维,维是不是数组中数的个数呢? 二、解答 维数是数组元素的下标个数。使⽤数组的时候,如果只有⼀个下标,则称为⼀维数组,⼀维数组⼀般表示⼀种线性数据的组合。⼆维数组则是有两个下标,可…...
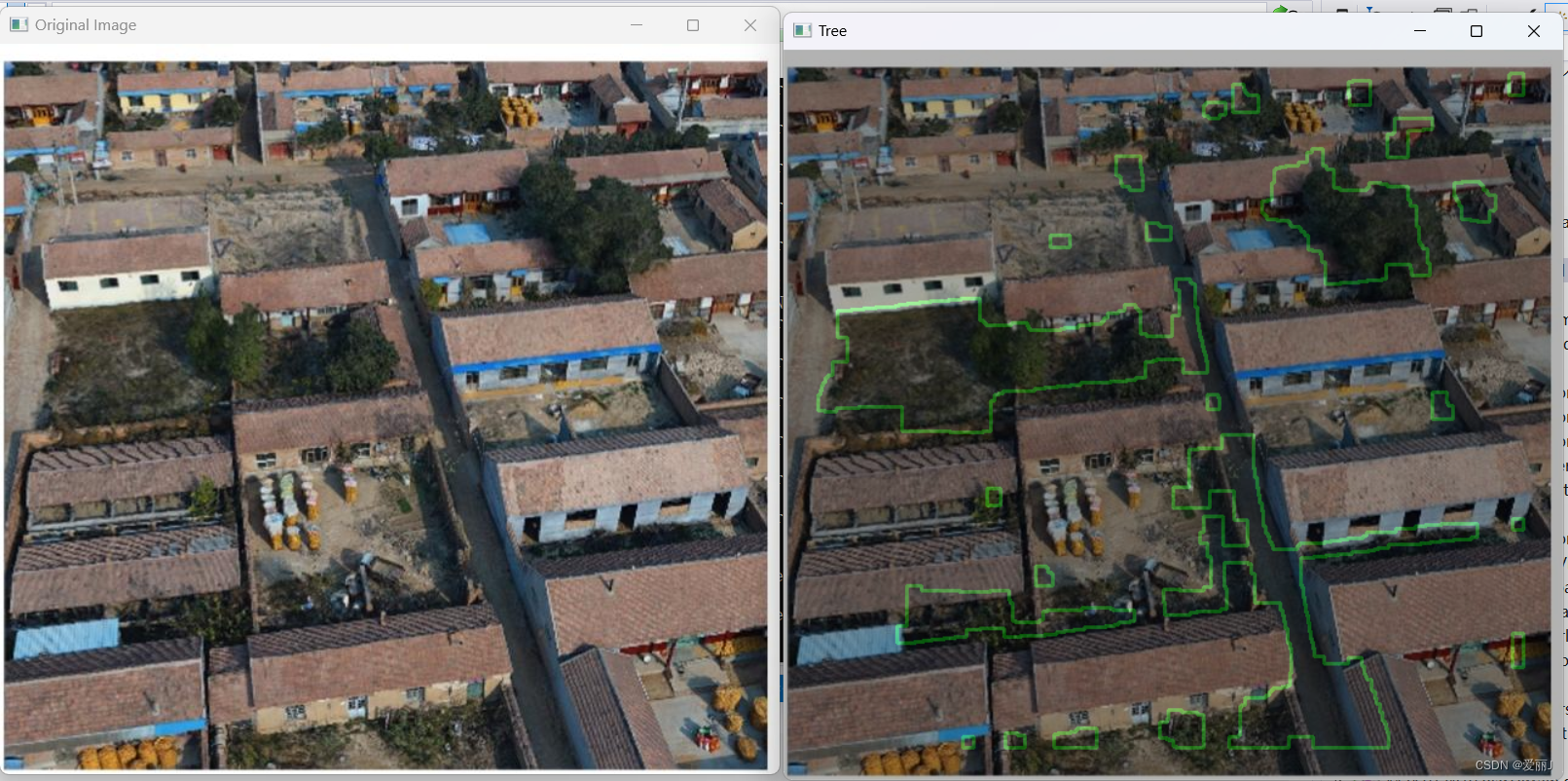
opencv解析系列 - 基于DOM提取大面积植被(如森林)
Note:简单提取,不考虑后处理(填充空洞、平滑边界等) #include <iostream> #include "opencv2/imgproc.hpp" #include "opencv2/highgui.hpp" #include <opencv2/opencv.hpp> using namespace cv…...

【Leetcode】299. 猜数字游戏
文章目录 题目思路代码结果 题目 题目链接 你在和朋友一起玩 猜数字(Bulls and Cows)游戏,该游戏规则如下: 写出一个秘密数字,并请朋友猜这个数字是多少。朋友每猜测一次,你就会给他一个包含下述信息的提…...

JWT身份验证
在实际项目中一般会使用jwt鉴权方式。 JWT知识点 jwt,全称json web token ,JSON Web令牌是一种开放的行业标准RFC 7519方法,用于在两方安全地表示声明。具体网上有许多文章介绍,这里做简单的使用。 1.数据结构 JSON Web Token…...

IOS面试题object-c 71-80
71. 简单介绍下NSURLConnection类及 sendSynchronousRequest:returningResponse:error:与– initWithRequest:delegate:两个方法的区别?NSURLConnection 主要用于网络访问,其中 sendSynchronousRequest:returningResponse:error:是同步访问数据,即当前…...

计算机mfc140.dll文件缺失的修复方法分析,一键修复mfc140.dll
电脑显示mfc140.dll文件缺失信息时,不必担心,这通常是个容易解决的小问题。接下来让我们详细探究并解决mfc140.dll文件缺失的状况。以下将详述相应的解决方案,从而帮助您轻松克服这一技术难题。通过几个简单步骤,即可恢复正常使用…...

web前端框架
目前比较火热的几门框架: React React是由Facebook(脸书)开发和创建的开源框架。React 用于开发丰富的用户界面,特别是当您需要构建单页应用程序时。它是最强大的前端框架。 弊端: 您不具备 JavaScript 的实践知识,则建议不要使用 React。同样&#x…...
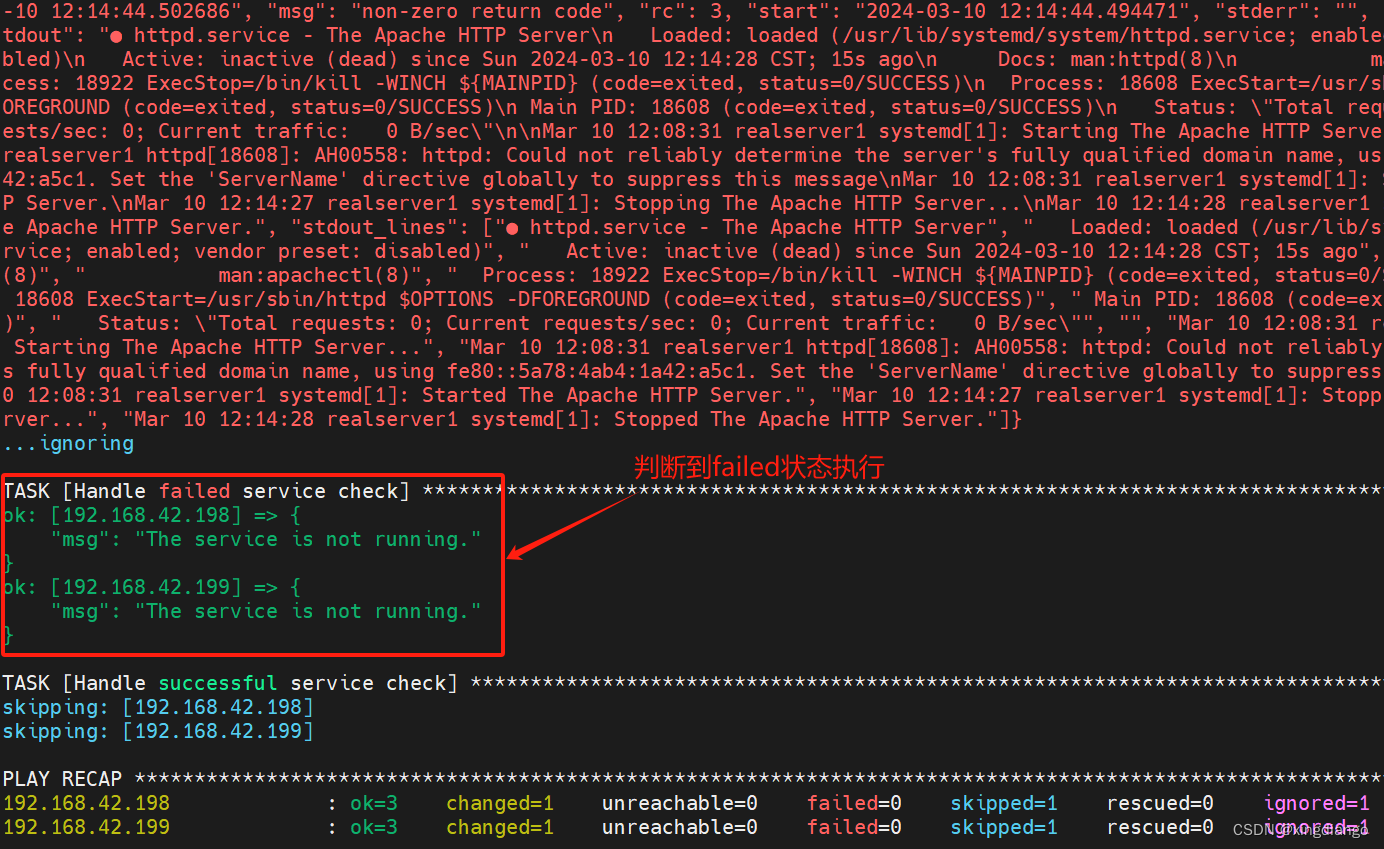
关于playbook中when条件过滤报The conditional check ‘result|failed‘ failed的问题
问题现象 在使用plabook中的when做过滤脚本如下: --- - hosts: realserversremote_user: roottasks:- name: Check if httpd service is runningcommand: systemctl status httpdregister: resultignore_errors: True- name: Handle failed service checkdebug:ms…...

【设计模式专题之抽象工厂模式】3. 家具工厂
题目描述 小明家新开了两个工厂用来生产家具,一个生产现代风格的沙发和椅子,一个生产古典风格的沙发和椅子,现在工厂收到了一笔订单,请你帮他设计一个系统,描述订单需要生产家具的信息。 输入描述 输入的第一行是一…...

架构:Apache Kafka Connect实现sqlserver数据实时同步
实现Apache Kafka Connect与SQL Server之间的实时数据同步,您可以使用Kafka Connect的JDBC Source Connector。以下是一个基本的步骤: 1. 安装Kafka Connect:确保您已经安装了Apache Kafka 和 Kafka Connect。您可以从Apache Kafka的官方网站…...
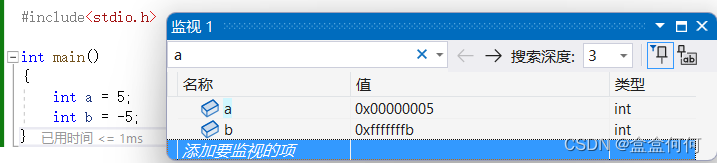
C语言:深入补码计算原理
C语言:深入补码计算原理 有符号整数存储原码、反码、补码转换规则数据与内存的关系 补码原理 有符号整数存储 原码、反码、补码 有符号整数的2进制表示方法有三种,即原码、反码和补码 三种表示方法均有符号位和数值位两部分,符号位用0表示“…...

【Pytorch】新手入门:基于sklearn实现鸢尾花数据集的加载
【Pytorch】新手入门:基于sklearn实现鸢尾花数据集的加载 🌈 个人主页:高斯小哥 🔥 高质量专栏:Matplotlib之旅:零基础精通数据可视化、Python基础【高质量合集】、PyTorch零基础入门教程👈 希望…...
maven项目引入私有jar,并打包到java.jar中
私有jar存放位置 maven依赖 <dependency><groupId>com.hikvision.ga</groupId><artifactId>artemis-http-client</artifactId><version>1.1.10</version><scope>system</scope><systemPath>${project.basedir}/s…...

Django中的Cookie和Session
文章目录 cookie是什么Django中如何使用cookieCookie使用示例session是什么Django中如何使用会话sessionSession使用示例小结 HTTP协议本身是”无状态”的,在一次请求和下一次请求之间没有任何状态保持,服务器无法识别来自同一用户的连续请求。有了cooki…...
)
Git-安装与使用(快速上手图文教程)
Git-安装与使用(快速上手图文教程) - 知乎 克隆: 首先你进去你要存放代码的位置,比如将代码存放到D盘,然后在D盘中右键,点击Git Bash Here,就是说本地仓库要在D盘建立。然后出现git 命令行界面…...
VBA_NZ系列工具NZ02:VBA读取PDF使用说明
我的教程一共九套及VBA汉英手册一部,分为初级、中级、高级三大部分。是对VBA的系统讲解,从简单的入门,到数据库,到字典,到高级的网抓及类的应用。大家在学习的过程中可能会存在困惑,这么多知识点该如何组织…...
所在的位置)
如何在paddlehub库中找到paddlehub.Module()所在的位置
要在PaddleHub库中找到paddlehub.Module()的位置,您可以通过以下步骤在PaddleHub库的源代码中进行查找: 1.确定PaddleHub库的安装位置:首先,确定您安装PaddleHub库的位置。通常,PaddleHub库会被安装在Python的site-pa…...

创建旅游景点图数据库Neo4J技术验证
文章目录 创建旅游景点图数据库Neo4J技术验证写在前面基础数据建库python3源代码KG效果KG入库效率优化方案PostGreSQL建库 创建旅游景点图数据库Neo4J技术验证 写在前面 本章主要实践内容: (1)neo4j知识图谱库建库。使用导航poi中的公园、景…...

Docker一键部署WordPress
使用Docker安装WordPress相对传统安装方式更加便捷高效,因为它可以快速创建一个包含所有必要组件(Web服务器、PHP和MySQL数据库)的独立容器环境。下面是一个简化的步骤说明如何使用Docker和Docker Compose安装WordPress: 一 安装…...
C++的类与对象(五):赋值运算符重载与日期类的实现
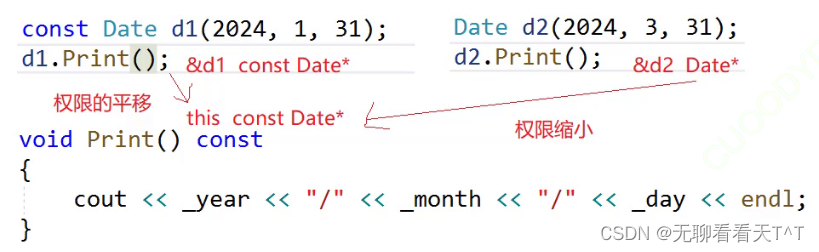
目录 比较两个日期对象 运算符重载 赋值运算符重载 连续赋值 日期类的实现 Date.h文件 Date.cpp文件 Test.cpp文件 const成员 取地址及const取地址操作符重载 比较两个日期对象 问题描述:内置类型可直接用运算符比较,自定义类型的对象是多个…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...
