高斯分布、高斯混合模型、EM算法详细介绍及其原理详解
相关文章
- K近邻算法和KD树详细介绍及其原理详解
- 朴素贝叶斯算法和拉普拉斯平滑详细介绍及其原理详解
- 决策树算法和CART决策树算法详细介绍及其原理详解
- 线性回归算法和逻辑斯谛回归算法详细介绍及其原理详解
- 硬间隔支持向量机算法、软间隔支持向量机算法、非线性支持向量机算法详细介绍及其原理详解
- 高斯分布、高斯混合模型、EM算法详细介绍及其原理详解
文章目录
- 相关文章
- 前言
- 一、高斯分布
- 二、高斯混合模型
- 三、EM算法
- 3.1 E步骤(Expectation)
- 3.2 M步骤(Maximization)
- 3.3 EM算法
- 总结
前言
今天给大家带来的主要内容包括:高斯分布,高斯混合模型,EM算法。废话不多说,下面就是本文的全部内容了!
一、高斯分布
小明是一所大学的老师,一次考试结束后,小明在统计两个班级同学的成绩:

其中,橙色的是一班的成绩,蓝色的是二班的成绩。但是,这次同学们非常调皮,都没有写上自己的名字和班级,这下给小明整不会了。他想:我能不能去猜一猜这些成绩里面,哪些是一班的,而哪些是二班的呢?

根据以往的经验,大多同学的成绩都分布在平均值左右,只有少数的同学考的非常好或者是非常不好,我们把这种概率分布叫做高斯分布:

描述高斯分布需要使用到两个参数:
- μ\muμ:描述数据的平均值,也被称为均值
- σ2\sigma^{2}σ2:描述数据的离散程度,也被称为方差

高斯分布的概率密度公式为:
P(x;μ,σ2)=12πσexp(−(x−μ)22σ2)P(x;\mu,\sigma^2)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp(-\dfrac{(x-\mu)^2}{2\sigma^2}) P(x;μ,σ2)=2πσ1exp(−2σ2(x−μ)2)
二、高斯混合模型
现在我们已经清楚了什么是高斯分布,那让我们再回到小明的例子:

因为这是两个班级的成绩,所以小明尝试使用两个高斯分布来拟合:
P(x∣γ1)=12πσ1exp(−(x−μ1)22σ12)P(x∣γ2)=12πσ2exp(−(x−μ2)22σ22)\begin{array}{c}P(x|\gamma_{1})=\dfrac{1}{\sqrt{2\pi}\sigma_1}\exp(-\dfrac{(x-\mu_1)^2}{2\sigma_1^2})\\ P(x|\gamma_{2})=\dfrac{1}{\sqrt{2\pi}\sigma_2}\exp(-\dfrac{(x-\mu_2)^2}{2\sigma_2^2})\end{array} P(x∣γ1)=2πσ11exp(−2σ12(x−μ1)2)P(x∣γ2)=2πσ21exp(−2σ22(x−μ2)2)
这样的模型也被称为高斯混合模型。 在这个模型里面:
- 如果我们知道哪些点来自一班或者是来自二班,那么我们就可以计算出来各自班级成绩的平均值和方差
- 如果我们知道各自班级成绩的平均值和方差,我们也可以大概猜出来哪些点是来自一班的,哪些点是来自二班的
这其实是一个鸡生蛋,蛋生鸡的问题:

如果我们有数据就可以来拟合分布,如果我们有了概率分布,就可以来判断数据的类别。但是,问题是我们现在什么都没有,应该怎么办呢?
三、EM算法
根据以上分析,我们现在什么数据都没有,还想对成绩进行分类,显然是有难度的。我们应该怎么办呢?既然我们没有数据,不如先做一个合适的假设来确定一部分的值。现在我们假设两个分布是这样的:

而且两个类别的先验概率是相等的。需要注意的是,以上这些都是假设,但是由于这些假设的存在,所以下式的值就是已知的量:
P(γ1)=P(γ2)=0.5P(\gamma_{1})=P(\gamma_{2})=0.5 P(γ1)=P(γ2)=0.5
3.1 E步骤(Expectation)
现在我们来评估一下每个成绩点是属于哪个班级的,对于第iii个数据xix_{i}xi来说:

根据贝叶斯定理,xix_{i}xi属于一班的概率是这样求的:
γi1=P(γi∣xi)=P(xi∣γ1)P(γ1)P(xi∣γ1)P(γ1)+P(xi∣γ2)P(γ2)\gamma_{i1}=P(\gamma_i|x_i)=\dfrac{P(x_i|\gamma_1)P(\gamma_1)}{P(x_i|\gamma_1)P(\gamma_1)+P(x_i|\gamma_2)P(\gamma_2)} γi1=P(γi∣xi)=P(xi∣γ1)P(γ1)+P(xi∣γ2)P(γ2)P(xi∣γ1)P(γ1)
上面的式子看似复杂,但是其中的每一项现在都是已知的,直接计算就可以了。现在已经得到了xix_{i}xi属于一班的概率,那么xix_{i}xi属于二班的概率就是1减去xix_{i}xi属于一班的概率:
γi2=P(γ2∣xi)=1−γi1\gamma_{i2}=P(\gamma_{2}|x_{i})=1-\gamma_{i1} γi2=P(γ2∣xi)=1−γi1
这样我们就可以给每一个点涂上对应的颜色,来表示它们可能属于的班级:

这一步被称为E步骤(Expectation),可以理解为求每一个点属于每个类别的期望值。
3.2 M步骤(Maximization)
此时,我们已经得到了每一个点属于每个班级的可能性,我们就可以重新校准两个班级的高斯分布了,也就是重新计算两个班级的平均值和方差:
-
一班:
μ1=γ11x1+γ21x1+…+γN1xNγ11+γ21+…+γN1σ12=γ11(x1−μ1)2+…+γN1(xN−μ1)2γ11+…+γN1\begin{array}{l}\mu_1=\frac{\gamma_{11}x_1+\gamma_{21}x_1+\ldots+\gamma_{N1}x_N}{\gamma_{11}+\gamma_{21}+\ldots+\gamma_{N1}}\\ \sigma_1^2=\frac{\gamma_{11}(x_1-\mu_1)^2+\ldots+\gamma_{N1}(x_N-\mu_1)^2}{\gamma_{11}+\ldots+\gamma_{N1}}\end{array} μ1=γ11+γ21+…+γN1γ11x1+γ21x1+…+γN1xNσ12=γ11+…+γN1γ11(x1−μ1)2+…+γN1(xN−μ1)2 -
二班:
μ2=γ12x1+γ22x1+…+γN2xNγ12+γ22+…+γN2σ22=γ12(x1−μ2)2+…+γN2(xN−μ2)2γ12+…+γN2\begin{array}{l}\mu_2=\frac{\gamma_{12}x_1+\gamma_{22}x_1+\ldots+\gamma_{N2}x_N}{\gamma_{12}+\gamma_{22}+\ldots+\gamma_{N2}}\\ \sigma_2^2=\frac{\gamma_{12}(x_1-\mu_2)^2+\ldots+\gamma_{N2}(x_N-\mu_2)^2}{\gamma_{12}+\ldots+\gamma_{N2}}\end{array} μ2=γ12+γ22+…+γN2γ12x1+γ22x1+…+γN2xNσ22=γ12+…+γN2γ12(x1−μ2)2+…+γN2(xN−μ2)2
同时,也可以更新两个班级的先验概率:
-
一班:
P(γ1)=γ11+…+γN1NP(\gamma_1)=\frac{\gamma_{11}+\ldots+\gamma_{N1}}{N} P(γ1)=Nγ11+…+γN1 -
二班:
P(γ2)=γ12+…+γN2NP(\gamma_2)=\frac{\gamma_{12}+\ldots+\gamma_{N2}}{N} P(γ2)=Nγ12+…+γN2
这一步被称为M步骤(Maximization),可以理解为,通过当前的数据求出最可能的分布参数。
3.3 EM算法
以上两个步骤合起来就是EM算法。当然,算法还没有结束,我们现在只是通过E和M两个步骤求出了两个班级的成绩分布的新的平均值和方差:

后面的工作就是重复E和M两个步骤:
- E步骤:根据两个班级的成绩分布更新点属于两个班级的可能性
- M步骤:更新两个班级的成绩分布的平均值和方差
一直重复以上两个步骤,直到两个成绩分布收敛不再被更新:

这样我们就得到了一个还不错的分类效果:

虽然和真实数据相比仍然有误差,不过也可以猜的八九不离十了:

这样,通过EM算法,小明的问题就可以被解决了。
总结
以上就是本文的全部内容了,学习EM算法还需要一些概率论与数理统计和高等数学的相关知识,所以读者最好提前温习一下。学习机器学习避免不了学习高等数学、线性代数、概率论与数理统计和矩阵论,所以读者一定要好好学习这几门课程!
相关文章:

高斯分布、高斯混合模型、EM算法详细介绍及其原理详解
相关文章 K近邻算法和KD树详细介绍及其原理详解朴素贝叶斯算法和拉普拉斯平滑详细介绍及其原理详解决策树算法和CART决策树算法详细介绍及其原理详解线性回归算法和逻辑斯谛回归算法详细介绍及其原理详解硬间隔支持向量机算法、软间隔支持向量机算法、非线性支持向量机算法详细…...
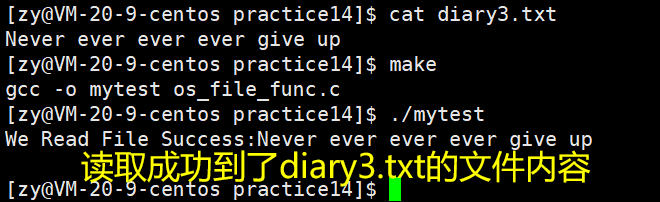
[Linux入门篇]一篇博客解决C/C++/Linux System Call文件操作接口的使用
目录 0.前言 1.C / C ->文件操作 1.1 C语言文件操作 1.1.1 C语言文件打开/关闭/写入 1.1.2 C语言文件的追加操作 1.1.3 C语言文件的读取 1.2 C语言文件操作 1.2.1 C文件打开 / 关闭 / 写入 1.2.2 C文件读取 1.2.3 文件追加 2.三个默认输入输出流 2.1 C语言中的三…...

数据结构和算法学习记录——删除有序数组中的重复项、合并两个有序数组
去重删除有序数组中的重复项题目来自:https://leetcode.cn/problems/remove-duplicates-from-sorted-array/description/题目描述给你一个 升序排列 的数组 nums ,请你原地删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数…...

FPGA实现模拟视频BT656解码 TW2867四路PAL采集拼接显示 提供工程源码和技术支持
目录1、前言2、模拟视频概述3、模拟视频颜色空间4、逐行与隔行5、BT656数据与解码BT656数据格式BT656数据解码6、TW2867芯片解读与配置TW2867芯片解读TW2867芯片配置TW2867时序分析7、设计思路与框架8、vivado工程详解9、上板调试验证10、福利:工程代码的获取1、前言…...
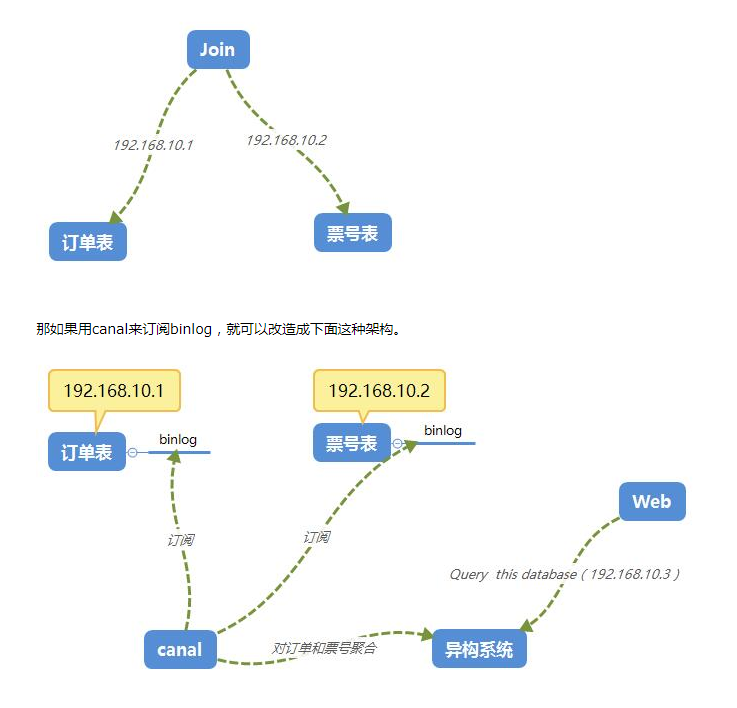
【建议收藏】超详细的Canal入门,看这篇就够了!!!
概述 canal是阿里巴巴旗下的一款开源项目,纯Java开发。基于数据库增量日志解析,提供增量数据订阅&消费,目前主要支持了MySQL(也支持mariaDB)。 背景 早期,阿里巴巴B2B公司因为存在杭州和美国双机房部…...

KubeSphere 社区双周报 | OpenFunction v1.0.0-rc.0 发布
KubeSphere 社区双周报主要整理展示新增的贡献者名单和证书、新增的讲师证书以及两周内提交过 commit 的贡献者,并对近期重要的 PR 进行解析,同时还包含了线上/线下活动和布道推广等一系列社区动态。 本次双周报涵盖时间为:2023.02.17-2023.…...

查漏补缺3月
SPI扩展序列化方式 分布式ID的相关问题 TCP的流量控制,避免浪费网络资源的滑动平均法也可以用在其他可能会出现资源浪费的情况等 讲一讲对自己这个 RPC 项目的想法,你是怎么设计这个项目的,想要实现那些功能? 你认为一个好的 RPC…...

如何使用Java实现类似Windows域登录
什么是域登录? 域登录是一种集中式身份验证和授权方法,用于访问企业内部网络和资源。在Windows环境中,域是一组计算机和用户帐户的集合,受到单个安全管理的控制。域登录允许用户在访问域资源时使用单个帐户名和密码进行身份验证&…...

生成模型与判别模型
生成模型与判别模型 一、决策函数Yf(X)或者条件概率分布P(Y|X) 监督学习的任务就是从数据中学习一个模型(也叫分类器),应用这一模型,对给定的输入X预测相应的输出Y。这个模型的一般形式为决策函数Yf(X)或者条件概率分布P(Y|X)。 …...

Kotlin lateinit 和 lazy 之间的区别 (翻译)
Kotlin 中的属性是使用var或val关键字声明的。Late init 和 lazy 都是用来初始化以后要用到的属性。 由于这两个关键字都用于声明稍后将要使用的属性,因此让我们看一下它们以及它们的区别。 Late Init 在下面的示例中,我们有一个变量 myClass࿰…...

Golang alpine Dockerfile 最小打包
最近在ubantu 上进行了 iris项目的alpine 版本打包,过程遇到了一些问题,记录一下。 golang版本 :1.18 系统:ubantu 代码结构 Dockfile内容 FROM alpine:latest MAINTAINER Si Wei<3320376695qq.com> ENV VERSION 1.1 ENV G…...
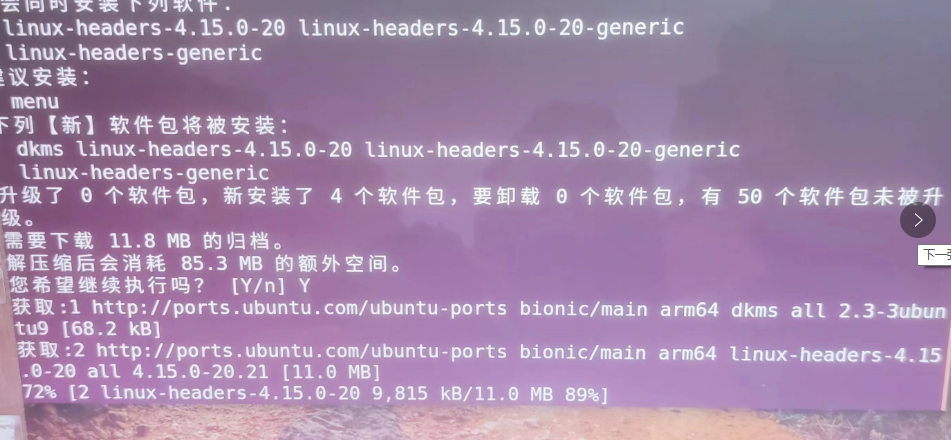
在NVIDIA JetBot Nano小车上更新WIFI驱动
前言:树莓派上的WIFI驱动类型比较多,经常有更好驱动的需求本文给出RealTek的无线WIFI模组,8821CU的驱动更新办法步骤第一 通过其他方式连接网络小车通过网线或者老的WIFI连接到网络上第二 构建驱动模块并下载驱动首先,我们需要打开一个ubuntu…...

2023年网络安全最应该看的书籍,弯道超车,拒绝看烂书
学习的方法有很多种,看书就是一种不错的方法,但为什么总有人说:“看书是学不会技术的”。 其实就是书籍没选对,看的书不好,你学不下去是很正常的。 一本好书其实不亚于一套好的视频教程,尤其是经典的好书…...

VSYNC研究
Vsync信号是SurfaceFlinger进程中核心的一块逻辑,我们主要从以下几个方面着手讲解。软件Vsync是怎么实现的,它是如何保持有效性的?systrace中看到的VSYNC信号如何解读,这些脉冲信号是在哪里打印的?为什么VSYNC-sf / VS…...

python gRPC:根据.protobuf文件生成py代码、grpc转换为http协议对外提供服务
文章目录python GRPC:根据.protobuf文件生成py代码grpcio-tools安装和使用python GRPC的官网示例grpc转换为http协议对外提供服务工作问题总结grpc-ecosystem/grpc-gateway/third_party/googleapis: warning: directory does not exist.python GRPC:根据…...
Allegro如何输出ODB文件操作指导
Allegro如何输出ODB文件操作指导 在PCB设计完成之后,需要输出生产文件用于生产加工,除了gerber文件可以用生产制造,ODB文件同样也可以用于生产,如下图 用Allegro如何输出ODB文件,具体操作如下 首先确保电脑上已经安装了ODB这个插件,版本不受限制点击File...
koa-vue的分页实现
1.引言 最近确实体会到了前端找工作的难处,不过大家还是要稳住心态,毕竟有一些前端大神说的有道理,前端发展了近20年,诞生了很多leader级别的大神,这些大神可能都没有合适的坑位,我们新手入坑自然难一些&am…...

安全开发基础 -- DAST,SAST,IAST简单介绍
安全开发基础-- DAST,SAST,IAST 简介 DAST 动态应用程序安全测试(Dynamic Application Security Testing)技术在测试或运行阶段分析应用程序的动态运行状态。它模拟黑客行为对应用程序进行动态攻击,分析应用程序的反…...
网络安全之暴力破解介绍及暴力破解Tomcat
网络安全之暴力破解介绍及应用场景一、暴力破解介绍1.1 暴力破解介绍1.2 暴力破解应用场景一、暴力破解Tomcat一、暴力破解介绍 1.1 暴力破解介绍 暴力破解字典:https://github.com/k8gege/PasswordDic 1.2 暴力破解应用场景 一、暴力破解Tomcat 登录Tomcat后台&a…...
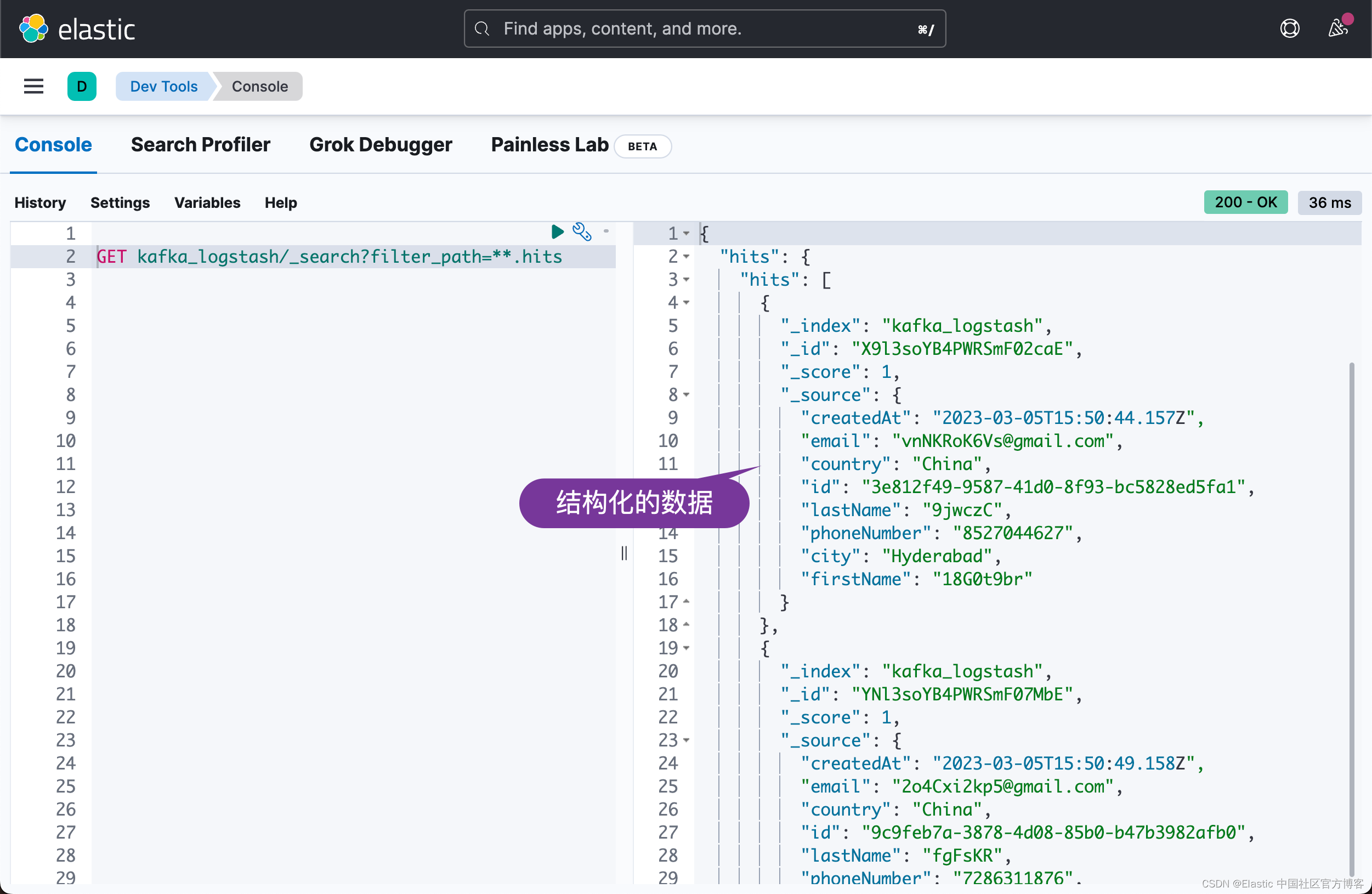
Elasticsearch:使用 Logstash 构建从 Kafka 到 Elasticsearch 的管道 - Nodejs
在我之前的文章 “Elastic:使用 Kafka 部署 Elastic Stack”,我构建了从 Beats > Kafka > Logstash > Elasticsearch 的管道。在今天的文章中,我将描述从 Nodejs > Kafka > Logstash > Elasticsearch 这样的一个数据流。在…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

Java中栈的多种实现类详解
Java中栈的多种实现类详解:Stack、LinkedList与ArrayDeque全方位对比 前言一、Stack类——Java最早的栈实现1.1 Stack类简介1.2 常用方法1.3 优缺点分析 二、LinkedList类——灵活的双端链表2.1 LinkedList类简介2.2 常用方法2.3 优缺点分析 三、ArrayDeque类——高…...
