Wilson威尔逊平滑
1、威尔逊平滑引入的动机
在曝光很少的情况下,计算出的CTR并不真实可靠,而样本数越大,CTR的比例才越准确,更能反应真实情况。
为了衡量样本数对于CTR信区间的影响,我们引入"威尔逊(Wilson)区间"的概念。Wilson区间的含义就是,就是指在一定置信度下,真实的CTR范围是多少。
2、威尔逊平滑公式

p —— 概率,即点击的概率,也就是 CTR
n —— 样本总数,即曝光数
z —— 在正态分布里,均值 + z * 标准差会有一定的置信度。例如 z 取 1.96,就有 95% 的置信度。
Wilson区间的含义就是,就是指在一定置信度下,真实的 CTR 范围是多少。
3、置信度区间z参数设置
置信度水平与区间的关系如下
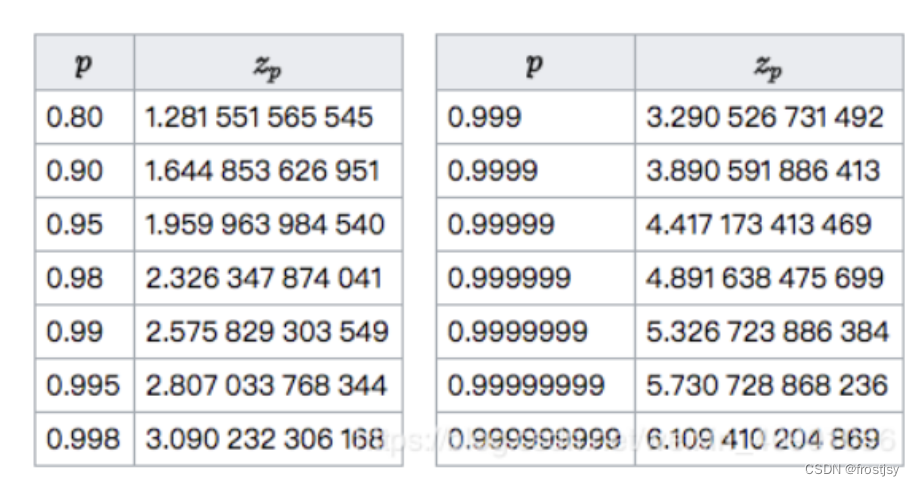
4、威尔逊几种实现代码
设置n小于多少时,认定为小样本,下面默认曝光次数小于10000时为小样本。
class WilsonCorrect(object):def evaluate(self, p, n, z=1.96, threshold=10000):score = pp = min(p, 1)if 0 < n < threshold:try:score = (p + z * z / (2 * n) - z / (2 * n) * math.sqrt(4 * n * (1 - p) * p + z * z)) / (1 + z * z / n)except:passreturn score当ctr大于某一阈值时,直接归0
import numpy as npdef walson_ctr(num_click, num_pv, z=1.96):p = num_click * 1.0 / num_pvif p > 0.9:return 0.0n = num_pvA = p + z**2 / (2*n)B = np.sqrt(p * (1-p) / n + z**2 / (4*(n**2)))C = z * BD = 1 + z**2 / nctr = (A - C) / Dreturn ctr全走wilson平滑
double walson_ctr(int num_pv, int num_click) {if (num_pv * num_click == 0 || num_pv < num_click) {return 0.f;}double score = 0.f;double z = 1.96f;int n = num_pv;double p = 1.0f * num_click / num_pv;score = (p + z*z/(2.f*n) - z*sqrt((p*(1.0f - p) + z*z /(4.f*n))/n)) / (1.f + z*z/n);return score;
}5、威尔逊实例
举个例子,有三个广告:
A:点击数 5 曝光数 10
B:点击数 50 曝光数 100
C:点击数 500 曝光数 1000
这三个广告的CTR 都是0.5 ,但是按照实际表现,从置信的角度分析,应该是C>B>A,因为C的样本数更多,可信度更高。
利用威尔逊平滑后的ctr预估值如下:
walson_ctr(5,10):0.2365895936154873
walson_ctr(50,100):0.40382982859014716
walson_ctr(500,1000):0.4690690341793595
6、参考文献
机器学习之数据处理威尔逊置信区间-CSDN博客
【推荐系统】推荐系统中一些常用的技术方法_威尔逊区间平滑-CSDN博客
相关文章:

Wilson威尔逊平滑
1、威尔逊平滑引入的动机 在曝光很少的情况下,计算出的CTR并不真实可靠,而样本数越大,CTR的比例才越准确,更能反应真实情况。 为了衡量样本数对于CTR信区间的影响,我们引入"威尔逊(Wilson࿰…...
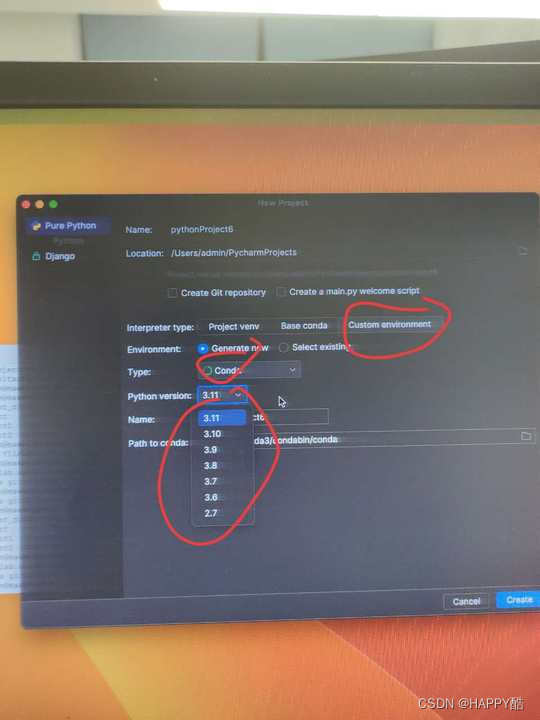
Mac测试环境搭建
1 下载pycharm 下载地址:PyCharm:JetBrains 出品的用于数据科学和 Web 开发的 Python IDE 2 安装python3.6.8 下载地址:Index of /ftp/python/3.6.8/ 安装后提示错误 换一种方式:用conda 下载地址:Free Download | …...

Jira自动化的实用工具——ScriptRunner简介及最佳实践
近日,龙智举办的DevSecOps研讨会年终专场“趋势展望与实战探讨:如何打好DevOps基础、赋能创新”在上海圆满落幕。龙智Atlassian技术与顾问咨询团队,以及清晖、JamaSoftware、CloudBees等生态伙伴的嘉宾发表了主题演讲,分享他们在D…...
App拉起微信小程序参考文章
App拉起微信小程序参考文章h5页面跳转小程序-----明文URL Scheme_weixin://dl/business/?appid*appid*&path*path*&qu-CSDN博客文章浏览阅读561次,点赞16次,收藏5次。仅需两步,就能实现h5跳转小程序,明文 URL Scheme&…...

AcWing 4956. 冶炼金属
对于这个题,V越大,除出来的数就越小,V越小,除出来的数就越大,当我们找一个最大和最小值的时候,就可以通过这个性质进行二分来求解。 可以通过求满足 [ A V ] [\frac{A}{V}] [VA] 小于等于 B B B的最小的…...

记一次面试经历
这段时间正好是金三银四的黄金时间段,正好这段时间也有很多企业有hc在招人,本文主要就是来聊聊我这段时间的面试经历吧。目前我是从北京投上海的岗位,现在有两家保底的offer。 简历投递 简历这块是基础也是必要的门槛,有没有面试…...
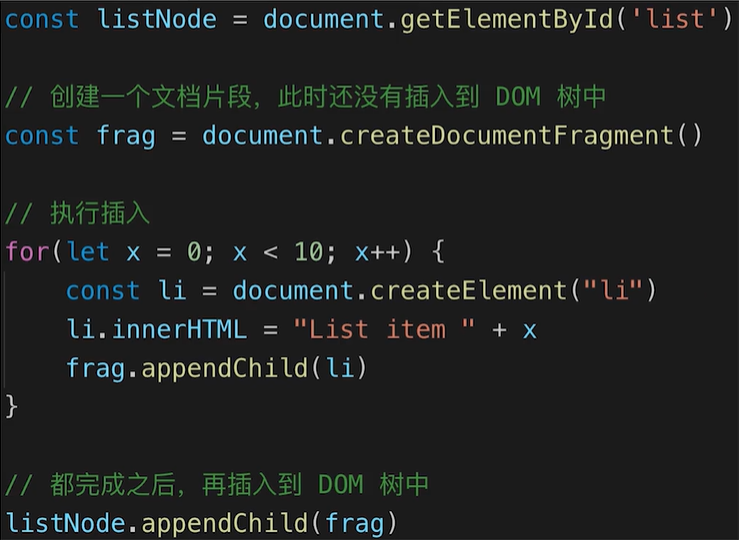
js【详解】DOM
文档对象模型(Document Object Model,简称DOM) DOM 是哪种数据结构 ? DOM 的本质是浏览器通过HTML代码解析出来的一棵 树。 操作 DOM 常用的 API 有哪些 ? 获取 DOM 节点 //方式 1:通过【id】获取…...
《互联网的世界》第六讲-去中心化和安全
互联网构建于开放互联的中立原则之上,公平接入,数据互联互通,流量被无差别对待,这意味着互联网本质上是匿名,去中心的,这与我们的现实世界完全不同。 但互联网上的主流业务却是 c/s 产销模式,试…...
nginx代理参数proxy_pass
proxy_pass参数用于配置反向代理,指定客户端请求被转发到后端服务器,后端地址可以是域名、ip端口URI 代理后端报错提示本地找不到CSS文件、JavaScript文件或图片 例如: nginx :10.1.74.109 后端服务:http://10.1.74.…...

_note_01
1.什么是跨平台 跨平台是指一个应用程序或一个编程语言,可以在不同的操作系统或平台上运行,而不需要对代码进行修改或重新编译。 跨平台应用程序或编程语言的设计和实现可以使开发者减少对特定平台的依赖,从而降低维护和开发的成本。同时&am…...

聊聊python中面向对象编程思想
面向对象编程思想 1、什么是面向过程 传统的面向过程的编程思想总结起来就八个字——自顶向下,逐步细化! → 将要实现的功能描述为一个从开始到结束按部就班的连续的“步骤” → 依次逐步完成这些步骤,如果某一个步骤的难度较大ÿ…...
MySQL-视图:视图概述、使用视图注意点、视图是否影响基本表
视图 一、视图概述二、使用视图注意点三、视图操作是否影响基本表 一、视图概述 在数据库管理系统中,视图(View)是一种虚拟表,它并不实际存储数据,而是基于一个或多个实际表的查询结果。视图提供了一种对数据库中数据…...
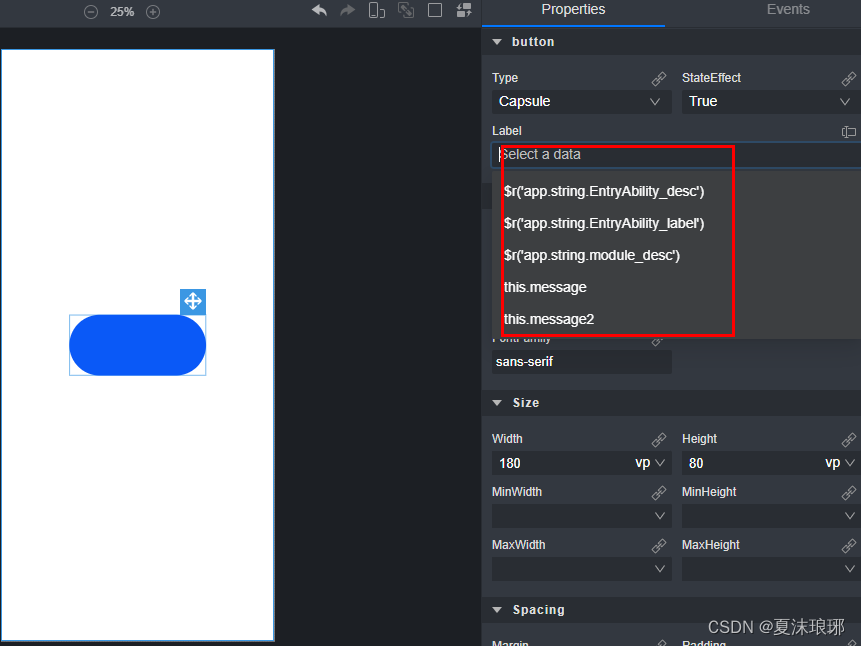
鸿蒙开发(四)-低代码开发
鸿蒙开发(四)-低代码开发 本文主要介绍下鸿蒙下的低代码开发。 鸿蒙低代码是指在鸿蒙操作系统进行应用开发时,采用简化开发流程和减少编码量的方式来提高开发效率。 1:开启低代码开发 首先我们打开DevEco Studio .然后创建工程。 如图所示ÿ…...
BUU [网鼎杯 2020 半决赛]AliceWebsite
BUU [网鼎杯 2020 半决赛]AliceWebsite 开题: hint附件是源码。在index.php中有一个毫无过滤的本地文件包含 <?php $action (isset($_GET[action]) ? $_GET[action] : home.php); if (file_exists($action)) {include $action; } else {echo "File not…...

超越 Siri 和 Alexa:探索LLM(大型语言模型)的世界
揭秘LLM:语言模型新革命,智能交互的未来趋势 近年来,虚拟助手的世界发生了重大转变。 虽然 Siri 和 Alexa 本身就是革命性的,但一种称为大型语言模型 (LLM) 的新型人工智能正在将虚拟助手的概念提升到一个全新的水平。 在这篇博文…...

Linux删除Mysql
//rpm包安装方式卸载 查包名:rpm -qa|grep -i mysql 删除命令:rpm -e –nodeps 包名//yum安装方式下载 1.查看已安装的mysql 命令:rpm -qa | grep -i mysql 2.卸载mysql 命令:yum remove mysql-community-server-5.6.36-2.el7.x86…...

CNN中常见的池化操作有哪些,作用是什么?
CNN中常见的池化操作有哪些,作用是什么? CNN中常见的池化操作只要是两种,平均值池化和最大值池化最大值池化常用于分类任务,是指在输入数据的局部区域内取最大值作为输出。最大池化的作用是降低特征图的尺寸,减少参数…...
能打印单据的软件,如进出库单据,物流快运单据,定制单据样式
能打印单据的软件,如进出库单据,物流快运单据,定制单据样式 一、前言 软件文件下载可以点击最下方官网卡片——软件下载——试用版软件下载 1、不同行业打印的单据不同 2、同一个行业打印的样式可能不同 3、有的行业已经印刷好了许多打印…...
uniapp列表进入动画
app列表入场动画 - DCloud 插件市场 列表入场动画https://ext.dcloud.net.cn/plugin?id16957...

FPGA TestBench编写学习
1 timescale 1.1 简介 timescale指令用于指定编译器在处理仿真时的时间单位和时间精度。这个指令通常在模块的顶层声明中使用,它告诉编译器和仿真器如何解释代码中的时间值。 timescale指令的语法如下: timescale <time_unit> <time_precis…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...
