机器学习100天（四十一）：041 对偶支持向量机-公式推导
《机器学习100天》完整目录：目录
机器学习 100 天，今天讲的是：对偶支持向量机-公式推导！
本节主要延续上一节的内容，推导线性支持向量机的对偶形式。本节内容包含的数学理论和推导很多，我尽量简化其中的数学部分，只做感性的介绍，便于大家在理解的同时不受数学复杂公式的阻挠。
上一节我们得到的结论，SVM的目标是：
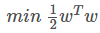
条件是：
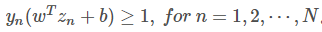
根据目标和条件，可以定义拉格朗日函数为：
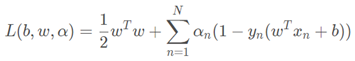
其中，等号右边第一项是目标，第二项是约束条件。 α n \alpha_n <
相关文章：
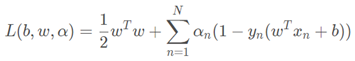
机器学习100天（四十一）：041 对偶支持向量机-公式推导
《机器学习100天》完整目录：目录 机器学习 100 天，今天讲的是：对偶支持向量机-公式推导！ 本节主要延续上一节的内容，推导线性支持向量机的对偶形式。本节内容包含的数学理论和推导很多，我尽量简化其中的数学部分，只做感性的介绍，便于大家在理解的同时不受数学复杂公式…...
函数)
C语言下的signal()函数
signal()简介 signal() 函数是 C 语言中用于处理系统信号的函数。它在 signal.h 头文件中进行声明。信号用作进程间通信，报告异常行为，例如除零，或用户的一些按键组合，例如同时按下 Ctrl 与 C 键，产生信号 SIGINT。 …...
google独立站和与企业官网的区别是什么？
google独立站和与企业官网的区别是什么？ 答案是：独立站通过谷歌SEO优化可以更好的获取自然排名的流量。 随着互联网的不断发展，企业越来越重视自身网站的建设和优化，而在企业网站建设中，很多人会犯一个常见的错误&am…...
Vue3---语法初探
目录 hello world 实现简易计时显示 反转字符串 显示隐藏 了解循环 了解双向绑定实现简易记事 设置鼠标悬停的文本 组件概念初探，进行组件代码拆分 hello world 最原始形态，找到 id 为 root 的标签，将 Vue 实例的模板放入标签之内 …...
esp8266WiFi模块通过MQTT连接华为云
esp8266WiFi模块通过MQTT连接华为云总结：一、 MQTT透传AT固件烧录二、 串口调试2.1 设置模块为STA模式2.2 连接WiFi2.3 设置MQTT的登陆用户名与密码2.4 设置MQTT的ClientID2.5 设置MQTT接入地址2.6 订阅设备属性上报的主题2.7 上传数据2.8 平台下发命令2.9 华为云物…...
苹果新卫星专利公布，苹果Find My功能知多少
根据美国商标和专利局（USPTO）公示的清单，苹果公司获得了一项新的卫星专利，可在非地面网络（Non-Terrestrial Networks，NTN）中定位用户设备（iDevice、MacBook 等）。 在专利…...
[ICLR‘22] DAB-DETR: Dynamic Anchor Boxes Are Better Queries for DETR
paper: https://arxiv.org/pdf/2201.12329.pdfcode: GitHub - IDEA-Research/DAB-DETR: [ICLR 2022] DAB-DETR: Dynamic Anchor Boxes are Better Queries for DETR将位置相关性计算显式的引入到decoder中，通过box坐标(x, y, w, h) 影响Q和K的相关性计算。特征图要有…...
双周赛99（贪心、数学、区间合并计算、换根DP）
文章目录双周赛99[6312. 最小和分割](https://leetcode.cn/problems/split-with-minimum-sum/)贪心[6311. 统计染色格子数](https://leetcode.cn/problems/count-total-number-of-colored-cells/)找规律[6313. 统计将重叠区间合并成组的方案数](https://leetcode.cn/problems/c…...
OpenText Exceed TurboX（ETX） 客户案例——弗吉尼亚理工大学
弗吉尼亚理工大学简化了高性能计算的使用。OpenText Exceed TurboX 提供高性能图形远程应用程序访问，提高工作效率 挑战 图形界面响应缓慢，影响用户使用； 对复制应用程序输出文件进行本地分析时，影响带宽和速度； 使用…...
【Python】torch.norm()用法解析
【Python】torch.norm()用法解析 文章目录【Python】torch.norm()用法解析1. 介绍1.1 p-范数1.2 Frobenius 范数1.3 核范数2. API3. 示例1. 介绍 torch.norm()是对输入的tensor求对应的范数。tensor的范数有以下三种： 1.1 p-范数 1.2 Frobenius 范数 即ÿ…...
)
C++核心编程＜内存分区模型＞(1)
C核心编程<内存分区模型>1.内存分区模型1.1内存分区模型概述1.2内存分区的意义1.3程序允许前1.3.1代码区1.3.2全局区1.3.2.1全局区的演示1.4程序运行后1.4.1栈区1.4.1.1栈区演示1.4.2堆区1.4.2.1堆区演示1.5new操作符1.5.1new操作的概述1.内存分区模型 1.1内存分区模型概…...
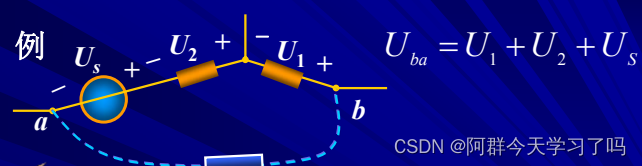
电路基础（1）电路模型和电路定律
电路中的电压、电流之间具有两种约束，一种是由电路元件决定的元件约束；另一种是元件间连接而引入的几何约束（就是拓扑约束），后者由基尔霍夫定律来表达。基尔霍夫定律是集总参数电路的基本定律。 1.电路和电路模型电源又…...
pytest 基础
pytest安装 安装 pip install -U pytest 验证安装 pytest --version 约束： 所有的测试文件名都需要满足test_ *.py格式或* _test.py格式。 测试文件中的测试类以Test_开头，并且不能带有 init 方法。 测试类中可以包含一个或多个test_开头的函数。 步骤…...
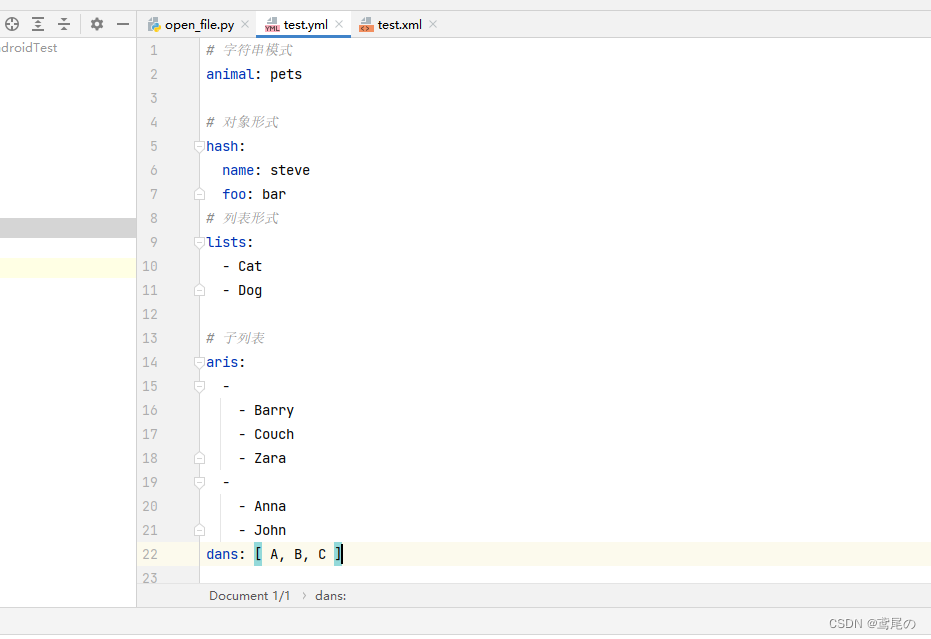
软测入门(七)python操作数据文件(Json、yaml、csv、excel、xml)
python操作文件 txt文件 read() : 读取所有readline() : 读取一行readlines() : 读取所有，且以行为单位，放入list列表中 file open(r"F:\abc.txt", "r", encoding"utf-8") # 以utf-8格式读取文件 # 读取所有 # print…...
【小程序】django学习笔记1
网页能用，不知道小程序能不能用。应该能吧。。。。。创建django程序文件包，xxx处是给该文件夹起个名django-admin startproject xxx一个project是由很多个app（小应用）组成的在文件夹目录下创建一个app，xxx处给该app起个…...
MySQL常用函数整理
MySQL常用函数整理sql函数分类一、流程控制1、判断值为null或空字符串2、IF函数3、IFNULL函数4、CASE函数(1) 相当于switch case的作用(2) 相当于if elseif的作用5、COALESCE函数二、字符串类（GBT答案）1、用于select、insert等子句中2、用于where子句中其…...
设计模式—“组件协作”
现代软件专业分工之后的第一个结果是“框架与应用程序的划分”，“组件协作”模式通过晚期绑定，来实现框架与应用程序之间的松耦合，是二者之间协作时常用的模式。 典型模式有：Template Method、Observer、Strategy 一、Template Method 动机 在软件构建过程中，对于某一…...
vue里使用driver.js实现项目功能向导指引
介绍 https://github.com/kamranahmedse/driver.js driver.js 是一个轻量级、无依赖的原生JavaScript引擎，在整个页面中驱动用户的注意力，强大的、高度可定制的原生JavaScript引擎，无外部依赖，支持所有主流浏览器。 安装 npm …...
详解JAVA类加载
目录 1.概述 2.双亲委派 3.ServiceClassLoader 4.URLClassLoader 5.加载冲突 1.概述 概念： 类加载器（Class Loader）是Java虚拟机（JVM）的一个重要组件，负责加载Java类到内存中并使其可以被JVM执行。类…...
高斯分布、高斯混合模型、EM算法详细介绍及其原理详解
相关文章 K近邻算法和KD树详细介绍及其原理详解朴素贝叶斯算法和拉普拉斯平滑详细介绍及其原理详解决策树算法和CART决策树算法详细介绍及其原理详解线性回归算法和逻辑斯谛回归算法详细介绍及其原理详解硬间隔支持向量机算法、软间隔支持向量机算法、非线性支持向量机算法详细…...
多云管理“拦路虎”：深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言：多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时，基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套：跨云网络构建数据…...
手游刚开服就被攻击怎么办？如何防御DDoS？
开服初期是手游最脆弱的阶段，极易成为DDoS攻击的目标。一旦遭遇攻击，可能导致服务器瘫痪、玩家流失，甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案，帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学（Elliptic Curve Cryptography）是基于椭圆曲线数学理论的公钥密码系统，由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA，ECC在相同安全强度下密钥更短（256位ECC ≈ 3072位RSA…...
遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...
macOS多出来了：Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台（Launchpad）多出来了：Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显，都是Google家的办公全家桶。这些应用并不是通过独立安装的…...
《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术，说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号（调制） 把信息从信号中抽取出来&am…...
OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成，核心是利用 HTTP 协议的 Range 请求头指定下载范围： 实现原理 Range 请求头：向服务器请求文件的特定字节范围（如 Range: bytes1024-） 本地文件记录：保存已…...
python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式（Python 实现） 在 Python 中，你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是，.doc 是旧的 Word 格式，而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...
2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来，实在找不到，希望有大佬教一下我。 还有就会议时间，我感觉不是图片时间，因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...
Spring Boot+Neo4j知识图谱实战：3步搭建智能关系网络！
一、引言 在数据驱动的背景下，知识图谱凭借其高效的信息组织能力，正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合，探讨知识图谱开发的实现细节，帮助读者掌握该技术栈在实际项目中的落地方法。 …...