扩散模型DDPM开源代码的剖析【对应公式与作者给的开源项目,diffusion model】
扩散模型DDPM开源代码的剖析【对应公式与作者给的开源项目,diffusion model】
- 一、简介
- 二、扩散过程:输入是x_0和时刻num_steps,输出是x_t
- 三、逆扩散过程:输入x_t,不断采样最终输出x_0
- 四、具体参考算法流程图
- 五、模型model和损失函数(最重要!)
- 1、先看损失函数
- 2、model(看解释)
- 六、损失函数的推导
一、简介
论文地址:https://proceedings.neurips.cc/paper/2020/hash/4c5bcfec8584af0d967f1ab10179ca4b-Abstract.html
项目地址:https://github.com/hojonathanho/diffusion
公式推导参考这篇博客:https://blog.csdn.net/qq_45934285/article/details/129107994?spm=1001.2014.3001.5502
本文主要对扩散模型的关键公式给出原代码帮助理解和学习。有pytorch和TensorFlow版。
原作者给的代码不太好理解,给出了pytorch的好理解一些。
二、扩散过程:输入是x_0和时刻num_steps,输出是x_t
首先值得注意的是:x_0是一个二维数组,例如这里给的是一个10000行2列的数组,即每一行代表一个点。
这里取了s_curve的x轴和z轴的坐标,用点表示看起来就像一个s型
s_curve,_ = make_s_curve(10**4,noise=0.1)
s_curve = s_curve[:,[0,2]]/10.0
dataset = torch.Tensor(s_curve).float()

扩散过程其实就是一个不断加噪的过程,其不含参。可以给出最终公式。
xt=α‾tx0x_t=\sqrt {\overline{\alpha}_ {t}}x_ {0}xt=αtx0 + 1−α‾t\sqrt {1-\overline {\alpha} }_ {t}1−αt z‾t\overline {z}_tzt
在t不断变大的时候βt\beta_tβt越来越大,αt=1−βt\alpha_t=1-\beta_tαt=1−βt越来越小。即t增大的时候上面公式的前一项系数越来越小,后一项系数越来越大不断接近一个z‾t\overline {z}_tzt的高斯分布。
代码来自diffusion_tf/diffusion_utils_2.py
def q_sample(self, x_start, t, noise=None):"""Diffuse the data (t == 0 means diffused for 1 step)"""if noise is None:noise = tf.random_normal(shape=x_start.shape)assert noise.shape == x_start.shapereturn (self._extract(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start +self._extract(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape) * noise)
pytorch:
#计算任意时刻的x采样值,基于x_0和重参数化
def q_x(x_0,t):"""可以基于x[0]得到任意时刻t的x[t]"""noise = torch.randn_like(x_0)# 创建了一个与 x_0 张量具有相同形状的名为 noise 的张量,并且该张量的值是从标准正态分布中随机采样得到的。alphas_t = alphas_bar_sqrt[t]alphas_1_m_t = one_minus_alphas_bar_sqrt[t]return (alphas_t * x_0 + alphas_1_m_t * noise)#在x[0]的基础上添加噪声
可见对于求xtx_txt的公式最难理解的就是代码如何实现z‾t\overline {z}_tzt在代码中是创建了一个与 x_0 张量具有**相同形状**的名为 noise 的张量,并且该张量的值是从标准正态分布中随机采样得到的。这个noise其元素的值是从均值为0、标准差为1的正态分布中随机采样得到的。这个张量可以被用于实现噪声注入,数据增强等操作,也可以被用于一些随机化的算法中。
值得一提的是原项目中用num_diffusion_timesteps=1000来表示t,假如num_steps=100,那么很多需要用到的参数都可以提前算出来。
三、逆扩散过程:输入x_t,不断采样最终输出x_0
最终公式是:
q(Xt−1∣XtX0)=N(Xt−1;1αt(Xt−βt(1−αˉt)Z),1−αˉt−11−αˉtβt),Z∼N(0,I)q\left(X_{t-1} \mid X_{t} X_{0}\right)=N\left(X_{t-1} ; \frac{1}{\sqrt{\alpha_t}} (X_{t}-\frac{\beta_{t}}{\sqrt{\left(1-\bar{\alpha}_{t}\right)}} Z), \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}} \beta_{t}\right), Z \sim N(0, I) q(Xt−1∣XtX0)=N(Xt−1;αt1(Xt−(1−αˉt)βtZ),1−αˉt1−αˉt−1βt),Z∼N(0,I)
在论文中方差设置为一个常数βt\beta _tβt或β~t\tilde{\beta }_tβ~t其中:
β~t=1−αˉt−11−αˉtβt\tilde{\beta }_t=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}} \beta_{t} β~t=1−αˉt1−αˉt−1βt
因此可训练的参数只存在与其均值之中。

就是这个公式,方差变为βt\beta_tβt,其中ϵθ\epsilon_\thetaϵθ是模型model
def p_sample(model,x,t,betas,one_minus_alphas_bar_sqrt):"""从x[T]采样t时刻的重构值"""t = torch.tensor([t])coeff = betas[t] / one_minus_alphas_bar_sqrt[t]eps_theta = model(x,t)mean = (1/(1-betas[t]).sqrt())*(x-(coeff*eps_theta))z = torch.randn_like(x)sigma_t = betas[t].sqrt()sample = mean + sigma_t * zreturn (sample)
代码来自diffusion_tf/diffusion_utils_2.py
def p_sample(self, denoise_fn, *, x, t, noise_fn, clip_denoised=True, return_pred_xstart: bool):"""Sample from the model"""model_mean, _, model_log_variance, pred_xstart = self.p_mean_variance(denoise_fn, x=x, t=t, clip_denoised=clip_denoised, return_pred_xstart=True)noise = noise_fn(shape=x.shape, dtype=x.dtype)assert noise.shape == x.shape# no noise when t == 0nonzero_mask = tf.reshape(1 - tf.cast(tf.equal(t, 0), tf.float32), [x.shape[0]] + [1] * (len(x.shape) - 1))sample = model_mean + nonzero_mask * tf.exp(0.5 * model_log_variance) * noiseassert sample.shape == pred_xstart.shapereturn (sample, pred_xstart) if return_pred_xstart else sample
循环恢复。
可见初始的x_t完全是一个随机噪声。torch.randn(shape)
cur_x可以看做是一个当前的采样,是一个二维数组,就是上面说的10000行2列。
然后x_seq可以看做是一个三维数组,即元素为cur_x的一个数组。
i是时刻,从n_steps的反向开始。
def p_sample_loop(model,shape,n_steps,betas,one_minus_alphas_bar_sqrt):"""从x[T]恢复x[T-1]、x[T-2]|...x[0]"""cur_x = torch.randn(shape)x_seq = [cur_x]for i in reversed(range(n_steps)):cur_x = p_sample(model,cur_x,i,betas,one_minus_alphas_bar_sqrt)x_seq.append(cur_x)return x_seq
代码来自diffusion_tf/diffusion_utils_2.py
def p_sample_loop(self, denoise_fn, *, shape, noise_fn=tf.random_normal):"""Generate samples"""assert isinstance(shape, (tuple, list))i_0 = tf.constant(self.num_timesteps - 1, dtype=tf.int32)img_0 = noise_fn(shape=shape, dtype=tf.float32)_, img_final = tf.while_loop(cond=lambda i_, _: tf.greater_equal(i_, 0),body=lambda i_, img_: [i_ - 1,self.p_sample(denoise_fn=denoise_fn, x=img_, t=tf.fill([shape[0]], i_), noise_fn=noise_fn, return_pred_xstart=False)],loop_vars=[i_0, img_0],shape_invariants=[i_0.shape, img_0.shape],back_prop=False)assert img_final.shape == shapereturn img_final
那么最终得到的x_seq就是最终从噪声恢复出的x_T到x_0序列。
恢复图像过程中利用了:
- βt\beta_tβt数组,其可以引申出很多参数(带α\alphaα的)
- num_steps即时刻。
- 一个model
参数只有model,那么我们来看model到底是什么。
四、具体参考算法流程图

五、模型model和损失函数(最重要!)
1、先看损失函数

其中x_0就是一个batch的数据,batch_size取x_0的行数,就是batch_size
值得注意的是这里t是一个列向量,那么a也是一个列向量,其与x_0相乘的时候用了,广播机制(第二列完全复制第一列)然后与x_0对应位置上的元素相乘。
def diffusion_loss_fn(model,x_0,alphas_bar_sqrt,one_minus_alphas_bar_sqrt,n_steps):"""对任意时刻t进行采样计算loss"""batch_size = x_0.shape[0] #对一个batchsize样本生成随机的时刻t 覆盖到更多不同的tt = torch.randint(0,n_steps,size=(batch_size//2,))t = torch.cat([t,n_steps-1-t],dim=0)# [batchsize]行向量t = t.unsqueeze(-1)#压缩最后的时刻1[batchsize,1]列向量 #x0的系数a = alphas_bar_sqrt[t] #eps的系数aml = one_minus_alphas_bar_sqrt[t] #生成随机噪音epse = torch.randn_like(x_0) #构造模型的输入x = x_0*a+e*aml #送入模型,得到t时刻的随机噪声预测值output = model(x,t.squeeze(-1)) #这里t又变为一维向量[batchsize] #与真实噪声一起计算误差,求平均值return (e - output).square().mean()
其调用过程见:
重要的:batch_x是dataset的一个batch_size行的数据。例如dataset是10000行,batch_size=128那么batch_x是dataset的128行。需要注意的是,如果 dataset 的大小不能被 batch_size 整除,那么最后一个批次的大小可能会小于 batch_size。即一个epoch的batch数量为dataset.size()/batch_size向上取整。
dataloader = torch.utils.data.DataLoader(dataset,batch_size=batch_size,shuffle=True)
for idx,batch_x in enumerate(dataloader):loss = diffusion_loss_fn(model,batch_x,alphas_bar_sqrt,one_minus_alphas_bar_sqrt,num_steps)
dataloader这行代码是使用 PyTorch 中的 DataLoader 函数来创建一个数据加载器对象。这个对象可以用来迭代访问输入数据,以便将其输入到神经网络中进行训练或评估。
dataset:一个包含输入数据和对应标签的数据集对象。这个对象需要实现 getitem 和 len 方法,以便能够通过索引或长度访问数据集中的数据。
batch_size:一个整数值,表示每个批次的数据量。
shuffle:一个布尔值,表示是否需要在每个 epoch 开始前随机打乱数据集中的数据。
这个函数返回的是一个数据加载器对象,可以通过迭代器的方式来访问其中的数据。例如,可以使用 for 循环来遍历整个数据集,每次迭代会返回一个批次的数据和对应的标签。这样就可以方便地将数据输入到神经网络中进行训练或评估。
for idx,batch_x in enumerate(dataloader):
这行代码是使用 enumerate 函数和 DataLoader 对象来遍历整个数据集,并按照 batch_size 的大小分成若干批次进行迭代。
具体来说,enumerate 函数用于同时返回迭代对象中的元素以及它们的索引。在这里,dataloader 对象就是要被迭代的对象,而 idx 变量则表示当前迭代的批次索引。batch_x 变量则是当前批次中的输入数据,它是一个包含 batch_size 个样本的张量对象。
需要注意的是,在使用 enumerate 函数时,可以通过设置 start 参数来指定起始索引的值,默认为 0。例如,如果设置 start=1,那么第一个迭代的索引就是 1 而不是 0
2、model(看解释)
这里给出了一个比较简单的model,论文中使用的是Unet结构的模型。具体可以参考:https://nn.labml.ai/diffusion/ddpm/unet.html
具体训练过程可以参考:https://nn.labml.ai/diffusion/ddpm/experiment.html
import torch
import torch.nn as nnclass MLPDiffusion(nn.Module):def __init__(self,n_steps,num_units=128):super(MLPDiffusion,self).__init__()self.linears = nn.ModuleList([nn.Linear(2,num_units),nn.ReLU(),nn.Linear(num_units,num_units),nn.ReLU(),nn.Linear(num_units,num_units),nn.ReLU(),nn.Linear(num_units,2),])self.step_embeddings = nn.ModuleList([nn.Embedding(n_steps,num_units),nn.Embedding(n_steps,num_units),nn.Embedding(n_steps,num_units),])
# 第6步的modeldef forward(self,x,t):
# x = x_0for idx,embedding_layer in enumerate(self.step_embeddings):t_embedding = embedding_layer(t)x = self.linears[2*idx](x)x += t_embeddingx = self.linears[2*idx+1](x)x = self.linears[-1](x)return x
首先:
batch_size = 128
dataloader = torch.utils.data.DataLoader(dataset,batch_size=batch_size,shuffle=True)
num_epoch = 4000 # 4000个散点图
plt.rc('text',color='blue')
model = MLPDiffusion(num_steps)#输出维度是2,输入是x和step
optimizer = torch.optim.Adam(model.parameters(),lr=1e-3)
然后:训练这个model
for t in range(num_epoch):for idx,batch_x in enumerate(dataloader):loss = diffusion_loss_fn(model,batch_x,alphas_bar_sqrt,one_minus_alphas_bar_sqrt,num_steps)optimizer.zero_grad()loss.backward()torch.nn.utils.clip_grad_norm_(model.parameters(),1.)optimizer.step()
该模型的参数包括多个线性层和Embedding层的权重和偏置,在代码中用nn.ModuleList保存。在优化器更新时,通过model.parameters()方法获取所有可更新的参数,包括线性层和Embedding层的权重和偏置。因此,优化器更新的参数就是这些权重和偏置。
全连接层可以对输入数据进行线性变换,并输出与变换后数据维度相同的结果。例如,对于输入向量 xxx,全连接层可以通过将其与权重矩阵 WWW 相乘,加上偏置向量 bbb,并应用某种非线性激活函数 σ\sigmaσ,来计算输出向量 yyy:
y=σ(Wx+b)y = \sigma(Wx + b)y=σ(Wx+b)
更新的是这个W和b
Embedding 的参数也是模型中需要被训练的权重矩阵,它的维度是 (vocab_size, embedding_dim),其中 vocab_size 是词汇表大小,embedding_dim 是词嵌入的维度。Embedding 的参数在训练过程中被不断地更新,以最小化模型在训练集上的损失函数。每个词都被编码成一个 embedding_dim 维的向量,这些向量将作为输入传递到后续的网络层中。Embedding 层通过学习将每个词映射到一个低维空间中的向量表示,从而使得相似的词在这个向量空间中也更加接近,提高了模型的泛化能力。
更新的是(vocab_size, embedding_dim)
optimizer.zero_grad()的作用是将模型参数的梯度清零。在每次反向传播计算梯度之前,需要先清除之前的梯度,否则之前计算的梯度会累加到当前计算中,导致梯度计算出错。因此,在每次训练之前,需要调用zero_grad()来清除梯度。
loss.backward()是PyTorch中用于计算梯度的函数。在神经网络训练中,首先需要将输入数据通过前向传递计算出预测值,然后根据预测值和真实标签计算出损失函数值。接下来,需要计算损失函数对于模型参数的梯度,以便使用优化算法对参数进行更新。==loss.backward()函数的作用就是计算损失函数对于所有需要梯度的参数的导数。==在调用该函数之前,需要将所有需要梯度计算的参数设置requires_grad=True。该函数计算得到的梯度会保存在参数的.grad属性中。通常,计算完梯度后需要对其进行裁剪,以避免梯度爆炸问题,然后使用优化器对模型参数进行更新。
torch.nn.utils.clip_grad_norm_()是PyTorch中用于梯度裁剪的函数。梯度裁剪是一种防止梯度爆炸的技术,它限制了梯度的最大范数,从而避免梯度值过大。函数的第一个参数是一个可迭代对象,通常是模型的参数列表,第二个参数是梯度的最大范数。在该代码中,model.parameters()返回模型的参数列表,1.指定了梯度的最大范数为1。因此,该函数的作用是将模型参数的梯度限制在最大范数为1的范围内。梯度裁剪通常在计算梯度后和参数更新之前进行,以保证梯度不会过大。
optimizer.step()是PyTorch中用于更新模型参数的函数。在每次梯度计算之后,需要使用优化器来更新模型的参数。优化器根据梯度和学习率等参数来计算参数更新的值,并将计算得到的值应用到模型参数中。调用optimizer.step()函数可以实现该操作。该函数会更新优化器内部的参数状态,以便下一次迭代使用。
在Python中,super() 函数是用来调用父类(超类)的一个方法。在面向对象编程中,通常使用 super() 函数来初始化父类的构造方法。在这里,super(MLPDiffusion,self).init() 调用了父类 nn.Module 的构造函数,相当于显式调用 nn.Module 的构造函数,初始化了当前类 MLPDiffusion 的基类 nn.Module。这样做是为了确保子类继承父类中的属性和方法,并且能够正确地使用它们。
for idx,embedding_layer in enumerate(self.step_embeddings):
这行代码是在遍历self.step_embeddings列表中的每个embedding层,同时记录下每个embedding层在列表中的索引idx。
在MLPDiffusion模型的forward函数中,self.step_embeddings是一个由三个Embedding层组成的ModuleList,每个Embedding层的作用是将当前时间步t转化为一个num_units维的向量。在模型的forward函数中,需要遍历这三个Embedding层,并将其输出的向量与模型的输入x相加。这样做的目的是为了将当前时间步t的信息融入到模型的计算中。因此,遍历每个Embedding层,并将其输出的向量与模型的输入x相加,是非常必要的。
x = self.linears[2*idx](x)
这行代码的作用是对模型的输入x进行线性变换,即将x通过一个全连接层(线性层)进行变换。其中,2idx表示要使用==第idx个Embedding层的输出,==而self.linears[2idx]则表示要使用与之对应的全连接层。
需要注意的是,由于self.linears是一个由多个层组成的ModuleList,而不是一个单独的层,因此需要通过下标来获取其中的某个层。2*idx表示要使用第idx个Embedding层的输出,因为每个Embedding层输出的维度都是num_units,所以输入到全连接层的维度也是num_units。这里采用的激活函数是ReLU。
第idx个Embedding层的输出是一个维度为(batch_size,num_units)的张量,表示对输入的时间步t进行了嵌入(embedding)后的结果。其中,batch_size表示输入数据的批次大小,num_units是预定义的嵌入向量的维度,这里为128。Embedding层将整数编码转换为密集向量,这些密集向量在整个模型的训练过程中逐渐学习得到,类似于单词的词向量。在本模型中,使用三个Embedding层分别嵌入了当前时间步t,前一时间步t-1和后一时间步t+1,这些嵌入向量会在全连接层中与输入向量x进行加权求和,以产生输出。
x = self.linears[-1](x)
这行代码对应的是在模型的最后一层加上一个全连接层,输出维度为2。该全连接层对前面所有层的输出进行线性变换,并输出一个维度为2的向量作为最终的预测值。
ReLU它是一个激活函数,用于在神经网络的前向传播过程中对输入进行非线性变换。ReLU函数的形式为f(x)=max(0,x)f(x) = \max(0, x)f(x)=max(0,x),可以将输入的负值部分清零,保留正值部分。在反向传播中,ReLU层的导数可以被有效地计算,因此可以通过反向传播算法对模型的其他参数进行更新。
六、损失函数的推导
我们根据负对数似然优化 ELBO(来自简森不等式)。
E[−logpθ(x0)]≤Eq[−logpθ(x0:T)q(x1:T∣x0)]=L\mathbb{E}[-\log \textcolor{lightgreen}{p_\theta}(x_0)] \le \mathbb{E}_q [ -\log \frac{\textcolor{lightgreen}{p_\theta}(x_{0:T})}{q(x_{1:T}|x_0)} ] \\ =L E[−logpθ(x0)]≤Eq[−logq(x1:T∣x0)pθ(x0:T)]=L
损失可以改写如下。
L=Eq[−logpθ(x0:T)q(x1:T∣x0)]=Eq[−logp(xT)−∑t=1Tlogpθ(xt−1∣xt)q(xt∣xt−1)]=Eq[−logp(xT)q(xT∣x0)−∑t=2Tlogpθ(xt−1∣xt)q(xt−1∣xt,x0)−logpθ(x0∣x1)]=Eq[DKL(q(xT∣x0)∥p(xT))+∑t=2TDKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))−logpθ(x0∣x1)]L = \mathbb{E}_q [ -\log \frac{\textcolor{lightgreen}{p_\theta}(x_{0:T})}{q(x_{1:T}|x_0)} ] \\ = \mathbb{E}_q [ -\log p(x_T) - \sum_{t=1}^T \log \frac{\textcolor{lightgreen}{p_\theta}(x_{t-1}|x_t)}{q(x_t|x_{t-1})} ] \\ = \mathbb{E}_q [ -\log \frac{p(x_T)}{q(x_T|x_0)} -\sum_{t=2}^T \log \frac{\textcolor{lightgreen}{p_\theta}(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)} -\log \textcolor{lightgreen}{p_\theta}(x_0|x_1)] \\ = \mathbb{E}_q [ D_{KL}(q(x_T|x_0) \Vert p(x_T)) +\sum_{t=2}^T D_{KL}(q(x_{t-1}|x_t,x_0) \Vert \textcolor{lightgreen}{p_\theta}(x_{t-1}|x_t)) -\log \textcolor{lightgreen}{p_\theta}(x_0|x_1)] L=Eq[−logq(x1:T∣x0)pθ(x0:T)]=Eq[−logp(xT)−t=1∑Tlogq(xt∣xt−1)pθ(xt−1∣xt)]=Eq[−logq(xT∣x0)p(xT)−t=2∑Tlogq(xt−1∣xt,x0)pθ(xt−1∣xt)−logpθ(x0∣x1)]=Eq[DKL(q(xT∣x0)∥p(xT))+t=2∑TDKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))−logpθ(x0∣x1)]
DKL(q(xT∣x0)∥p(xT))D_{KL}(q(x_T|x_0) \Vert p(x_T))DKL(q(xT∣x0)∥p(xT)) 是常数,因为我们保持 β1,…,βT\beta_1, \dots, \beta_Tβ1,…,βT 不变。
计算 Lt−1=DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))L_{t-1} = D_{KL}(q(x_{t-1}|x_t,x_0) \Vert \textcolor{lightgreen} {p_\theta}(x_{t-1}| x_t))Lt−1=DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))
以 x0x_0x0 为条件的前向过程后验是,
q(xt−1∣xt,x0)=N(xt−1;μ~t(xt,x0),β~tI)μ~t(xt,x0)=αˉt−1βt1−αˉtx0+αt(1−αˉt−1)1−αˉtxtβ~t=1−αˉt−11−αˉtβtq(x_{t-1}|x_t, x_0) = \mathcal{N} \Big(x_{t-1}; \tilde\mu_t(x_t, x_0), \tilde\beta_t \mathbf{I} \Big) \\ \tilde\mu_t(x_t, x_0) = \frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1 - \bar\alpha_t}x_0 + \frac{\sqrt{\alpha_t}(1 - \bar\alpha_{t-1})}{1-\bar\alpha_t}x_t \\ \tilde\beta_t = \frac{1 - \bar\alpha_{t-1}}{1 - \bar\alpha_t} \beta_t q(xt−1∣xt,x0)=N(xt−1;μ~t(xt,x0),β~tI)μ~t(xt,x0)=1−αˉtαˉt−1βtx0+1−αˉtαt(1−αˉt−1)xtβ~t=1−αˉt1−αˉt−1βt
该论文设置 Σθ(xt,t)=σt2I\textcolor{lightgreen}{\Sigma_\theta}(x_t, t) = \sigma_t^2 \mathbf{I}Σθ(xt,t)=σt2I 其中 σt2\sigma_t^2σt2 设置为常量 βt\beta_tβt 或 β~t\tilde\beta_tβ~t。
然后,
pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),σt2I)\textcolor{lightgreen}{p_\theta}(x_{t-1} | x_t) = \mathcal{N}\big(x_{t-1}; \textcolor{lightgreen}{\mu_\theta}(x_t, t), \sigma_t^2 \mathbf{I} \big)pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),σt2I)
对于给定噪声 ϵ∼N(0,I)\epsilon\sim\mathcal{N}(\mathbf{0}, \mathbf{I})ϵ∼N(0,I) 使用 q(xt∣x0)q(x_t|x_0)q(xt∣x0)
xt(x0,ϵ)=αˉtx0+1−αˉtϵx0=1αˉt(xt(x0,ϵ)−1−αˉtϵ)x_t(x_0, \epsilon) = \sqrt{\bar\alpha_t} x_0 + \sqrt{1-\bar\alpha_t}\epsilon \\ x_0 = \frac{1}{\sqrt{\bar\alpha_t}} \Big(x_t(x_0, \epsilon) - \sqrt{1-\bar\alpha_t}\epsilon\Big) xt(x0,ϵ)=αˉtx0+1−αˉtϵx0=αˉt1(xt(x0,ϵ)−1−αˉtϵ)
这给出了:
Lt−1=DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))=Eq[12σt2∥μ~(xt,x0)−μθ(xt,t)∥2]=Ex0,ϵ[12σt2∥1αt(xt(x0,ϵ)−βt1−αˉtϵ)−μθ(xt(x0,ϵ),t)∥2]L_{t-1} = D_{KL}(q(x_{t-1}|x_t,x_0) \Vert \textcolor{lightgreen}{p_\theta}(x_{t-1}|x_t)) \\ = \mathbb{E}_q \Bigg[ \frac{1}{2\sigma_t^2} \Big \Vert \tilde\mu(x_t, x_0) - \textcolor{lightgreen}{\mu_\theta}(x_t, t) \Big \Vert^2 \Bigg] \\ = \mathbb{E}_{x_0, \epsilon} \Bigg[ \frac{1}{2\sigma_t^2} \bigg\Vert \frac{1}{\sqrt{\alpha_t}} \Big( x_t(x_0, \epsilon) - \frac{\beta_t}{\sqrt{1 - \bar\alpha_t}} \epsilon \Big) - \textcolor{lightgreen}{\mu_\theta}(x_t(x_0, \epsilon), t) \bigg\Vert^2 \Bigg] \\ Lt−1=DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))=Eq[2σt21μ~(xt,x0)−μθ(xt,t)2]=Ex0,ϵ[2σt21αt1(xt(x0,ϵ)−1−αˉtβtϵ)−μθ(xt(x0,ϵ),t)2]
使用模型重新参数化以预测噪声
μθ(xt,t)=μ~(xt,1αˉt(xt−1−αˉtϵθ(xt,t)))=1αt(xt−βt1−αˉtϵθ(xt,t))\textcolor{lightgreen}{\mu_\theta}(x_t, t) = \tilde\mu \bigg(x_t, \frac{1}{\sqrt{\bar\alpha_t}} \Big(x_t - \sqrt{1-\bar\alpha_t}\textcolor{lightgreen}{\epsilon_\theta}(x_t, t) \Big) \bigg) \\ = \frac{1}{\sqrt{\alpha_t}} \Big(x_t - \frac{\beta_t}{\sqrt{1-\bar\alpha_t}}\textcolor{lightgreen}{\epsilon_\theta}(x_t, t) \Big) μθ(xt,t)=μ~(xt,αˉt1(xt−1−αˉtϵθ(xt,t)))=αt1(xt−1−αˉtβtϵθ(xt,t))
其中 ϵθ\epsilon_\thetaϵθ 是一个学习函数,它在给定 (xt,t)(x_t, t)(xt,t) 的情况下预测 ϵ\epsilonϵ。
这给出了:
Lt−1=Ex0,ϵ[βt22σt2αt(1−αˉt)∥ϵ−ϵθ(αˉtx0+1−αˉtϵ,t)∥2]L_{t-1} = \mathbb{E}_{x_0, \epsilon} \Bigg[ \frac{\beta_t^2}{2\sigma_t^2 \alpha_t (1 - \bar\alpha_t)} \Big\Vert \epsilon - \textcolor{lightgreen}{\epsilon_\theta}(\sqrt{\bar\alpha_t} x_0 + \sqrt{1-\bar\alpha_t}\epsilon, t) \Big\Vert^2 \Bigg] Lt−1=Ex0,ϵ[2σt2αt(1−αˉt)βt2ϵ−ϵθ(αˉtx0+1−αˉtϵ,t)2]
也就是说,我们正在训练预测噪声。
Simplified loss
Lsimple(θ)=Et,x0,ϵ[∥ϵ−ϵθ(αˉtx0+1−αˉtϵ,t)∥2]L_{\text{simple}}(\theta) = \mathbb{E}_{t,x_0, \epsilon} \Bigg[ \bigg\Vert \epsilon - \textcolor{lightgreen}{\epsilon_\theta}(\sqrt{\bar\alpha_t} x_0 + \sqrt{1-\bar\alpha_t}\epsilon, t) \bigg\Vert^2 \Bigg]Lsimple(θ)=Et,x0,ϵ[ϵ−ϵθ(αˉtx0+1−αˉtϵ,t)2]
这最小化 −logpθ(x0∣x1)-\log \textcolor{lightgreen}{p_\theta}(x_0|x_1)−logpθ(x0∣x1) when t=1t=1t=1 和 Lt−1L_{t-1}Lt−1 for t>1t\gt1t>1 丢弃 在 Lt−1L_{t-1}Lt−1 中加权。丢弃权重 βt22σt2αt(1−αˉt)\frac{\beta_t^2}{2\sigma_t^2 \alpha_t (1 - \bar\alpha_t)}2σt2αt(1−αˉt)βt2 增加赋予较高 ttt(具有较高噪声水平)的权重,从而提高样本质量。
如果觉得有帮助的话,记得点赞收藏支持一下哦。如果有问题请在评论区一起交流讨论。
Reference:
https://www.bilibili.com/video/BV1b541197HX/?spm_id_from=333.999.0.0
https://nn.labml.ai/diffusion/ddpm/index.html
相关文章:

扩散模型DDPM开源代码的剖析【对应公式与作者给的开源项目,diffusion model】
扩散模型DDPM开源代码的剖析【对应公式与作者给的开源项目,diffusion model】一、简介二、扩散过程:输入是x_0和时刻num_steps,输出是x_t三、逆扩散过程:输入x_t,不断采样最终输出x_0四、具体参考算法流程图五、模型mo…...

C语言 学生记录管理系统
学生记录管理系统 1--添加 2--删除 3--查询:按姓名 4--查询:按班级 5--查询:按学号 0--退出 请选择操作序号(0—5):1 请输入新学生的学号:1 请输入新学生的…...

【独家】华为OD机试 C 语言解题 - 交换字符
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 最近更新的博客使用说明本期…...

网络安全平台测试赛 easyphp(phar脏数据处理)
昨天的比赛,14.00-17.00.时间有点紧张,比赛期间没拿下来这道 😭非常痛苦,很顺畅的思路 一步步想下来,卡在最后一步末尾脏数据处理了,最后时间到了 没打通,还需多练 这里本地复现一下࿱…...

【python】XML格式文件读写详解
注:最后有面试挑战,看看自己掌握了吗 文章目录XML介绍格式XML与AJAX与HTML区别联系生成XML文件案例用SAX模块处理XML用DOM模块处理XML🌸I could be bounded in a nutshell and count myself a king of infinite space. 特别鸣谢:…...

理解js的精度问题
参考博客:js精度丢失问题-看这篇文章就够了(通俗易懂)、探寻 JavaScript 精度问题以及解决方案、JavaScript 浮点数陷阱及解法 1 为什么 JavaScript 中所有数字包括整数和小数都只有一种类型 即 Number类型,它的实现遵循 IEEE 754 标准。 符号位S&#…...

蓝桥杯 时间显示
题目 输入输出样例 示例 1 输入 46800999输出 13:00:00示例 2 输入 1618708103123输出 01:08:23评测用例规模与约定 对于所有评测用例,给定的时间为不超过 10^{18}1018 的正整数。 运行限制 最大运行时间:1s最大运行内存: 512M 基础知识 时间的转换…...

qt中设置菜单高度
如题所示,我建立一个菜单,代码如下,但是菜单项的高度太小了, { popupMenu new QMenu(this); QAction *action1 new QAction(tr(“&New1”), this); QAction *action2 new QAction(tr(“&New2”), this); QA…...

测开:前端基础-css页面布局-定位
一 、传统网页布局的三种方式 网页布局的本质–用CSS来摆放盒子,把盒子摆放到相应的位置,css提供了三种传统布局方式,分别是标准流,浮动和定位三种。 二、 定位 2.1 啥是定位 我的理解,就是要把这个元素,…...

Servlet中八个监听器介绍
一、监听对象创建的监听器 1、ServletContextListener /*** 用于监听ServletContext对象创建和销毁的监听器* since v 2.3*/public interface ServletContextListener extends EventListener {/*** 对象创建时执行此方法。该方法的参数是ServletContextEvent事件对象…...
LicenseBox Crack,对服务器的要求最低
LicenseBox Crack,对服务器的要求最低 LicenseBox是用于管理基于PHP的软件、WordPress插件或主题、主题、插件和WordPress的更新和许可的完整软件。它易于安装,对服务器的要求最低,用户友好的界面,无限脚本的使用为您的创造力打开了大门。 Li…...

css中重难点整理(vertical-align)
一、vertical-align 在学习vertical-align的时候,可能会很困惑。即使网上有一大推文章讲veitical-align,感觉看完好像懂了,等自己布局的时候用到vertical-align的时候好像对它又很陌生。这就是我在布局的时候遇到的问题。 本来vertical-align就很不好理…...

javaScript基础面试题 ---宏任务微任务
宏任务微任务一、为什么JS是单线程语言?二、JS是单线程,怎样执行异步代码?1、JS是单线程语言 2、JS代码执行流程,同步执行完,再进行事件循环(微任务、宏任务) 3、清空所有的微任务,再…...
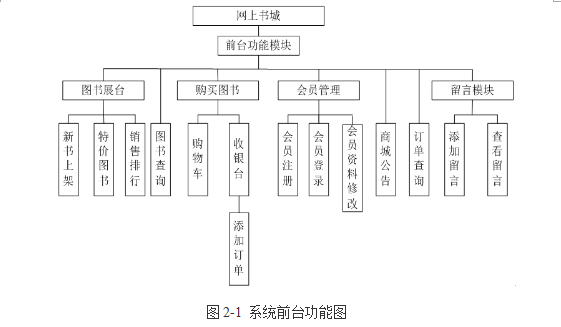
基于JSP的网上书城
技术:Java、JSP等摘要:随着科技的迅速发展,计算机技术已应用到社会的各个领域。随着计算机技术和通信技术的迅速发展,网络的规模也逐渐增大,网络的元素也随之不断增加,有的利用其通信,有的利用其…...

C#教程 05 常量
文章目录 C# 常量整数常量浮点常量字符常量字符串常量定义常量C# 常量 常量是固定值,程序执行期间不会改变。常量可以是任何基本数据类型,比如整数常量、浮点常量、字符常量或者字符串常量,还有枚举常量。 常量可以被当作常规的变量,只是它们的值在定义后不能被修改。 整数…...
)
【华为OD机试真题java、python】基站维修工程师【2022 Q4 100分】(100%通过)
代码请进行一定修改后使用,本代码保证100%通过率。本文章提供java、python两种代码 题目描述 小王是一名基站维护工程师,负责某区域的基站维护。 某地方有 n 个基站( 1<n<10 ),已知各基站之间的距离 s( 0<s<500 ), 并且基站 x 到基站 y 的距离,与基站 y …...

你是真的“C”——为冒泡排序升级赋能!
你是真的“C”——为冒泡排序升级赋能!😎前言🙌冒泡排序升级赋能之境界一!冒泡排序升级赋能之境界二!qsort库函数的运用和认识总结撒花💞😎博客昵称:博客小梦 😊最喜欢的…...

【JavaEE】基于mysql与servlet自制简易的表白墙程序
文章目录1 表白墙页面构建2 Servlet 回顾3 表白墙后端程序实现3.1 我们需要做什么?3.2 实现细节4 实现结果写在最后1 表白墙页面构建 该页面由标题、文本、三个 input 输入框与一个提交按钮构成,整体比较简单,相关样式文件和页面代码会在后面…...
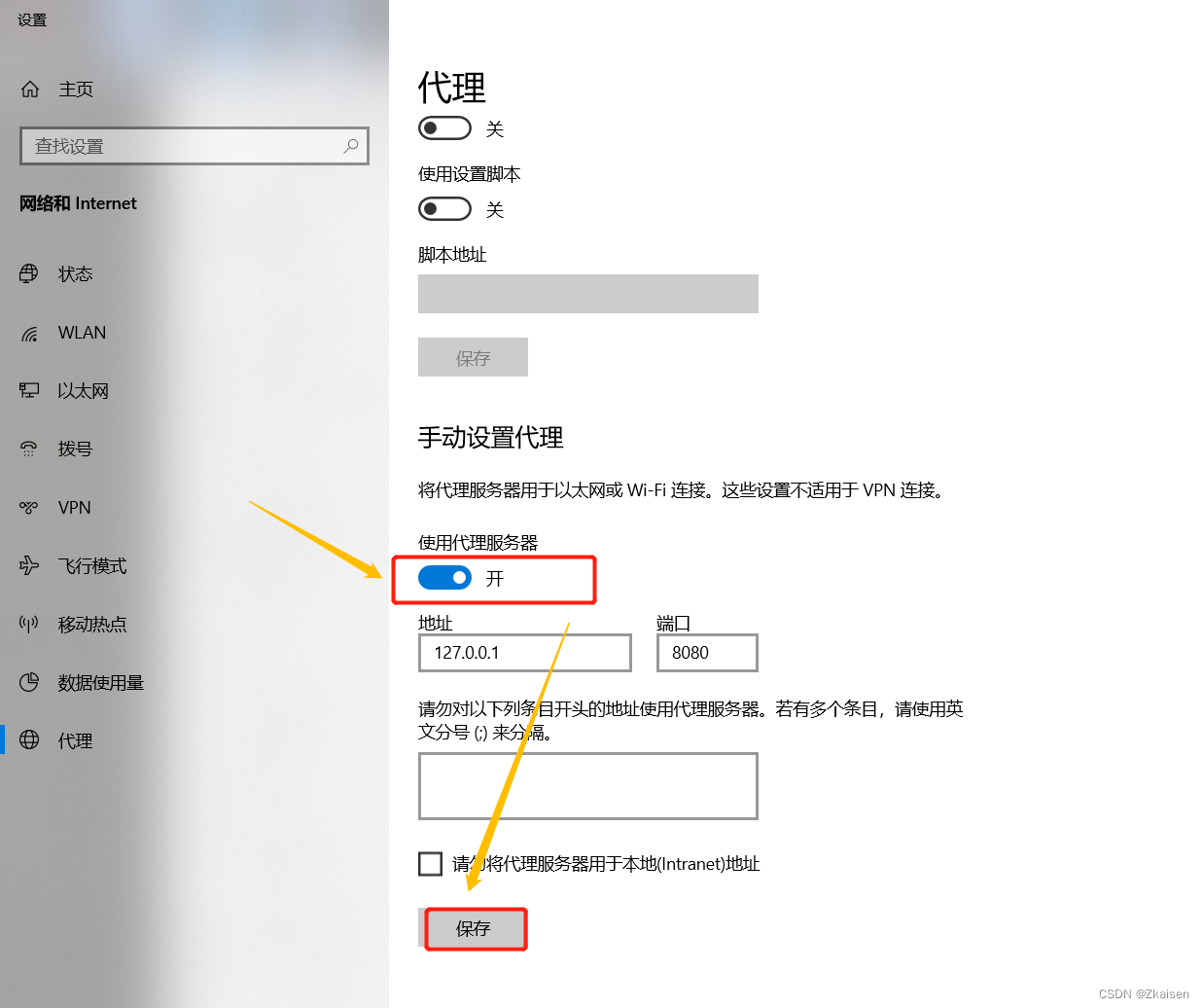
抓包技术(浏览器APP小程序PC应用)
P1 抓包工具 01. Fidder 首先第一个Fiddler它的优势,独立运行,第二个支持移动设备(是否能抓移动APP的包,)在这一块的话wireshark、httpwatch就不支持,因此在这一块就可以排除掉前连个,因为我们…...
linux笔记(10):ubuntu环境下,基于SDL2运行lvgl+ffmpeg播放mp4
文章目录1.ubuntu安装ffmpeg1.1 源码安装1.1 克隆ffmpeg源码1.2 配置编译条件,编译,安装1.2 直接安装依赖包2.下载lvgl源码2.1 测试原始代码2.2 运行lv_example_ffmpeg_2()例程2.2.1 配置 LV_USE_FFMPEG 为 12.2.2 lv_example_ffmpeg_2()替换lv_demo_wid…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...

MLP实战二:MLP 实现图像数字多分类
任务 实战(二):MLP 实现图像多分类 基于 mnist 数据集,建立 mlp 模型,实现 0-9 数字的十分类 task: 1、实现 mnist 数据载入,可视化图形数字; 2、完成数据预处理:图像数据维度转换与…...
