有趣的数学 毕达哥拉斯定理
随便找个学生,让他举出一位著名的数学家——如果他能想到的话,他往往会选择毕达哥拉斯。如果不是,也许他想到的是阿基米德。哪怕是杰出的艾萨克·牛顿,在两位古代世界的巨星面前也只能叨陪末座了。阿基米德是一位思想巨人,毕达哥拉斯或许算不上,但人们往往低估了他的贡献,他值得更多赞誉——不在于他做出了什么,而在于他推动了什么。
在公元前570年左右,毕达哥拉斯出生在爱琴海东部的希腊萨摩斯岛。他是一位哲学家和几何学家。我们对他的生活所知甚少,而且信息都来自很久之后的记述,其历史准确性存疑,但关键事件很可能是对的。公元前530年左右,他搬到古希腊殖民地克罗顿(今意大利)。他在那里创立了一个哲学宗教团体——“毕达哥拉斯学派”,他们相信宇宙是基于数字的。时至今日,其创始人的名声就来自以他的名字命名的定理。这个定理已被教授了两千多年,还进入了流行文化。

由于历史的不可考,现代人并不知道毕达哥拉斯是否真的证明了他的定理。事实上,根本不知道这是否是他的定理。它完全有可能是毕达哥拉斯的一个仆从,或某个古巴比伦或苏美尔的抄写员发现的。但人们把它归功于毕达哥拉斯,他的名字就流传下来了。无论其起源如何,这个定理和它的结果对人类历史产生了巨大的影响。它们的的确确拓展了我们的世界。
古希腊人并没有将毕达哥拉斯定理表达为现代符号意义上的等式。那是随着代数的发展才出现的。在古代,该定理以口头和几何的方式表达。亚历山大里亚的欧几里得的著作记载了它最优雅的形式,这也是它的第一个文献证据。公元前250年左右,欧几里得写下了著名的《几何原本》——有史以来最具影响力的数学教科书,成为第一位现代数学家。
欧几里得把几何学变成了逻辑:他明确地列出了自己的基本假设,并援引这些假设,为他的所有定理提供系统的证明。他建造了一座概念之塔,其基础是点、线和圆,而塔尖则恰好存在五种正多面体。
欧几里得几何“王冠上的明珠”就是我们现在所说的毕达哥拉斯定理:《几何原本》第一卷中的命题47。在托马斯·希思爵士的著名译本中,这个命题是这样写的:“在直角三角形中,直角所对的边上的正方形等于夹直角的边上的两个正方形。”
就高等数学而言,古希腊人使用的是直线和面积,而不是数字。所以毕达哥拉斯和他的古希腊后人将这个定理解释为面积相等:“用直角三角形中最长边构造的正方形面积,是由另外两边构造的正方形面积的和。”最长的一条边就是著名的“斜边”(hypotenuse),意思是“在下面拉伸”。如果你以恰当的方向画图,确实如此,如下图(左)所示。
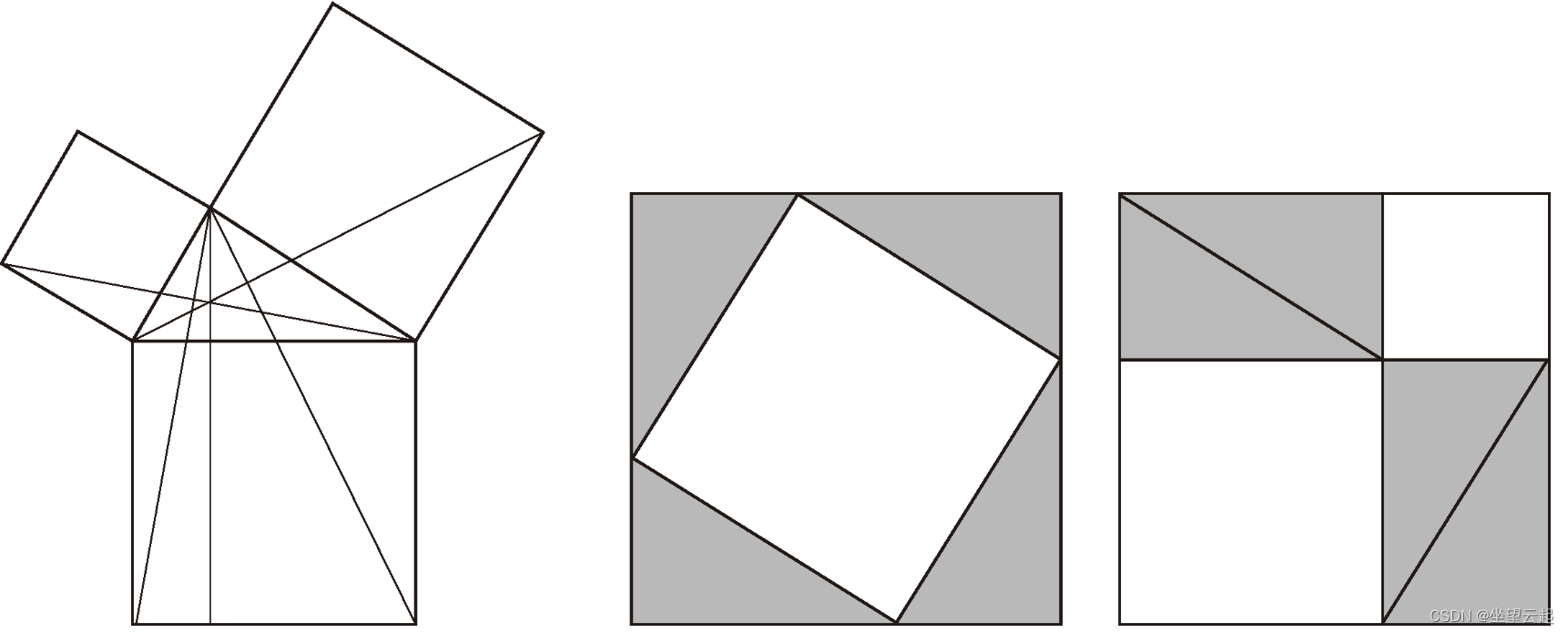
左:欧几里得证明毕达哥拉斯定理的构造线。中和右:定理的另一证明。外部正方形的面积相等,阴影三角形的面积也相等。因此,倾斜的白色正方形面积等于其他两个白色正方形面积之和。
2000年后,毕达哥拉斯定理就被重写为代数方程,毕达哥拉斯方程有许多用途和意义。最直接的是,给定另外两边,它可以让你计算斜边的长度。
我们在现实生活中遇到的许多三角形都不是直角三角形,因此方程的直接应用似乎有限。但是,任何三角形都可以分割成两个直角三角形,而任何多边形都可以分割成若干三角形。因此,直角三角形是关键:它们证明了三角形的形状与其边的长度之间存在有用的关系。从这一见解中发展出来的学科是三角学——“三角形的测量”。
直角三角形是三角学的基础,特别是它决定了基本的三角函数:正弦、余弦和正切。这些名称源于阿拉伯语,而这些函数及其许多前辈的发展史,展示了今天这个版本经历了什么样的复杂路径。
欧几里得《几何原本》中的毕达哥拉斯定理的证明,把这个定理牢牢地限定在欧氏几何的范围内。“欧氏几何”这个词一度可以直接换成“几何”,因为我们通常认为欧氏几何就是物理空间的真实几何。
但事实并非如此,后面若干年又发展出来椭圆几何(黎曼几何)、罗氏几何(双曲几何)等,都是非欧几里得几何,并且这些新的几何与欧氏几何一样逻辑自洽,遵循了除了平行公理之外的所有公理。
相关文章:
有趣的数学 毕达哥拉斯定理
随便找个学生,让他举出一位著名的数学家——如果他能想到的话,他往往会选择毕达哥拉斯。如果不是,也许他想到的是阿基米德。哪怕是杰出的艾萨克牛顿,在两位古代世界的巨星面前也只能叨陪末座了。阿基米德是一位思想巨人࿰…...

理解记忆相关
foreach循环 在 Java 中,foreach 循环(也称为增强型 for 循环)是一种简洁的语法,用于遍历数组或集合(如 List、Set、Map 等)。以下是 foreach 循环的基本用法: 遍历数组: String[] …...

零基础学习JS--基础篇--使用对象
JavaScript 的设计是一个简单的基于对象的范式。一个对象就是一系列属性的集合,一个属性包含一个名和一个值。一个属性的值可以是函数,这种情况下属性也被称为方法。除了浏览器里面预定义的那些对象之外,你也可以定义你自己的对象。本章节讲述…...
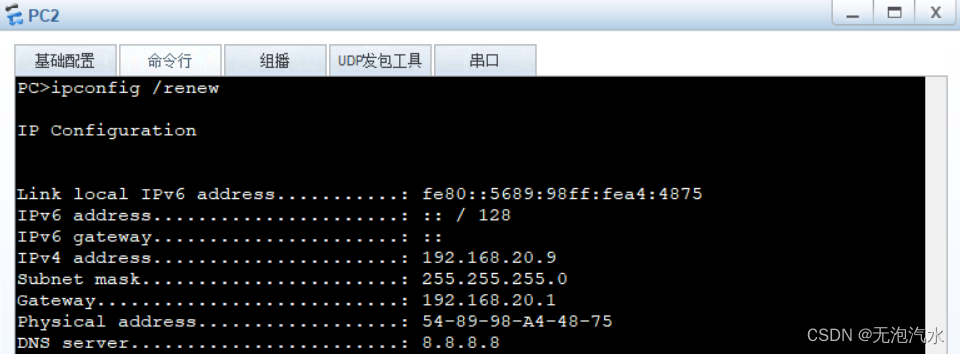
DHCP中继实验(华为)
思科设备参考:DHCP中继实验(思科) 一,技术简介 DHCP中继,可以实现在不同子网和物理网段之间处理和转发DHCP信息的功能。如果DHCP客户机与DHCP服务器在同一个物理网段,则客户机可以正确地获得动态分配的IP…...

【数据结构】初识二叉搜索树(Binary Search Tree)
文章目录 1. 二叉搜索树的概念2. 二叉搜索树的操作1.1 二叉搜索树的查找1.2 二叉搜索树的插入1.3 二叉搜索树的删除 1. 二叉搜索树的概念 二叉搜索树又称二叉排序树,它可能是一棵空树,也可能是具有以下性质的二叉树: 若它的左子树不为空&am…...

数据库系统概念(第一周)
⚽前言 🏐四个基本概念 一、数据 定义 种类 特点 二、数据库 三、数据库管理系统(DBMS) 四、 数据库系统(DBS) 🏀数据库系统和文件系统对比 文件系统的弊端 🥎数据视图 数据抽象 …...
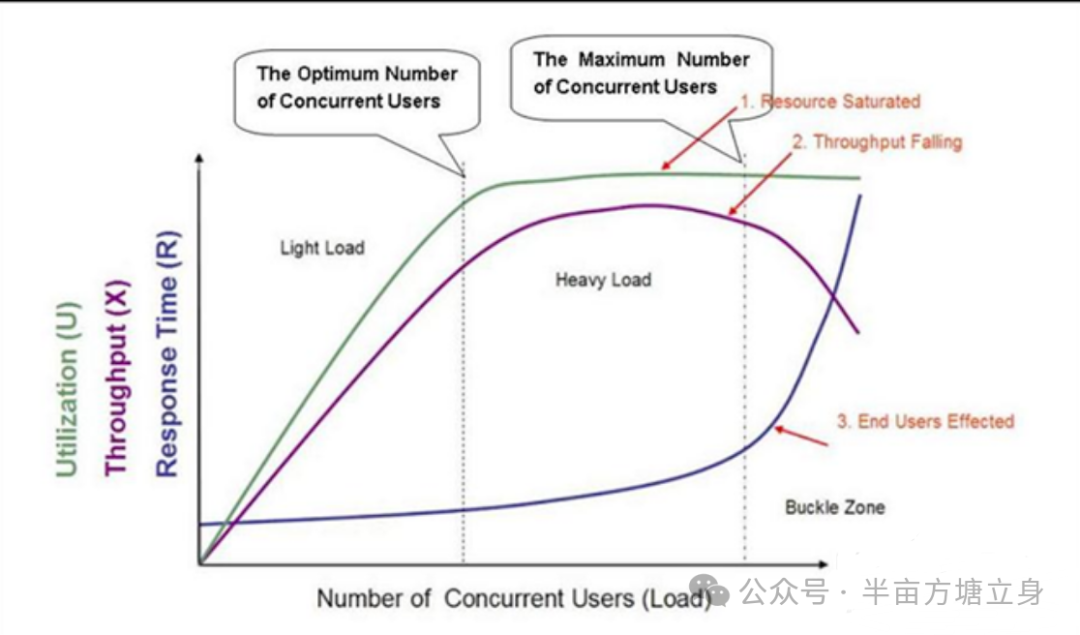
如何确定限流阈值:面试官问我,我怎么答?
在面试过程中,系统高并发是经常需要考察的,而熔断限流又是必考的,当面试官问及如何确定限流的阈值时,他们实际上是在考察你是否理解限流的本质及其在实际工作中是否有过经验。限流是一种常用的系统保护措施,用于防止过…...
)
HW干货集合 | HW面试题记录(1)
整理最近护网面试问的问题 前言 一开始会问问你在工作中负责的是什么工作(如果在职),参与过哪些项目。还有些会问问你之前有没有护网的经历,如果没有的话一般都会被定到初级(技术特牛的另说)。下面就是一…...
数据集踩的坑及解决方案汇总
数据集踩的坑及解决方案汇总 数据集各种格式构建并训练自己的数据集汇总Yolo系列SSDMask R-CNN报错 NotADirectoryError: [Errno 20] Not a directory: /Users/mia/Desktop/P-Clean/mask-RCNN/PennFudanPed2/labelme_json/.DS_StoreFaster R-CNN数据的格式转换划分数据集设定内…...

机器学习流程—数据预处理 Encoding
机器学习流程—数据预处理 Encoding 在机器学习中,我们经常会遇到分类变量,这些分量变量往往机器学习模型没有办法从中学习,往往有两种,一种是字符型,一种是数值型。通常需要对分类型变量做一些处理,常用的方法有两种:label encoding和one hot encoding。 例如,假设数…...

04-微服务 面试题
目录 1.Spring Cloud 常见的组件有哪些? 2.服务注册和发现是什么意思?(Spring Cloud 如何实现服务注册发现) 3.你们项目负载均衡如何实现的 ? 4.什么是服务雪崩,怎么解决这个问题? 5.你们服务是怎么监控的? 6.微服务限流(漏桶算法、令牌桶算法) 7.解释一下CAP…...

Qt连接所有同类部件到同一个槽函数
void MainWindow::AutoConnectSignals() {// 查找所有 QSpinBoxconst auto spinBoxes findChildren<QSpinBox*>();for (auto *spinBox : spinBoxes){connect(spinBox, static_cast<void(QSpinBox::*)(int)>(&QSpinBox::valueChanged), this, &ParameterW…...

spring boot 使用 webservice
spring boot 使用 webservice 使用 java 自带的 jax-ws 依赖 如果是jdk1.8,不需要引入任何依赖,如果大于1.8 <dependency><groupId>javax.jws</groupId><artifactId>javax.jws-api</artifactId><version>1.1</version&g…...

【嵌入式】嵌入式系统稳定性建设:最后的防线
🧑 作者简介:阿里巴巴嵌入式技术专家,深耕嵌入式人工智能领域,具备多年的嵌入式硬件产品研发管理经验。 📒 博客介绍:分享嵌入式开发领域的相关知识、经验、思考和感悟。提供嵌入式方向的学习指导、简历面…...
【算法】一类支持向量机OC-SVM
【算法】一类支持向量机OC-SVM 前言一类支持向量机OC-SVM 概念介绍示例编写数据集创建实现一类支持向量机OC-SVM完整的示例输出 前言 由于之前毕设期间主要的工具就是支持向量机,从基础的回归和分类到后来的优化,在接触到支持向量机还有一类支持向量机的…...
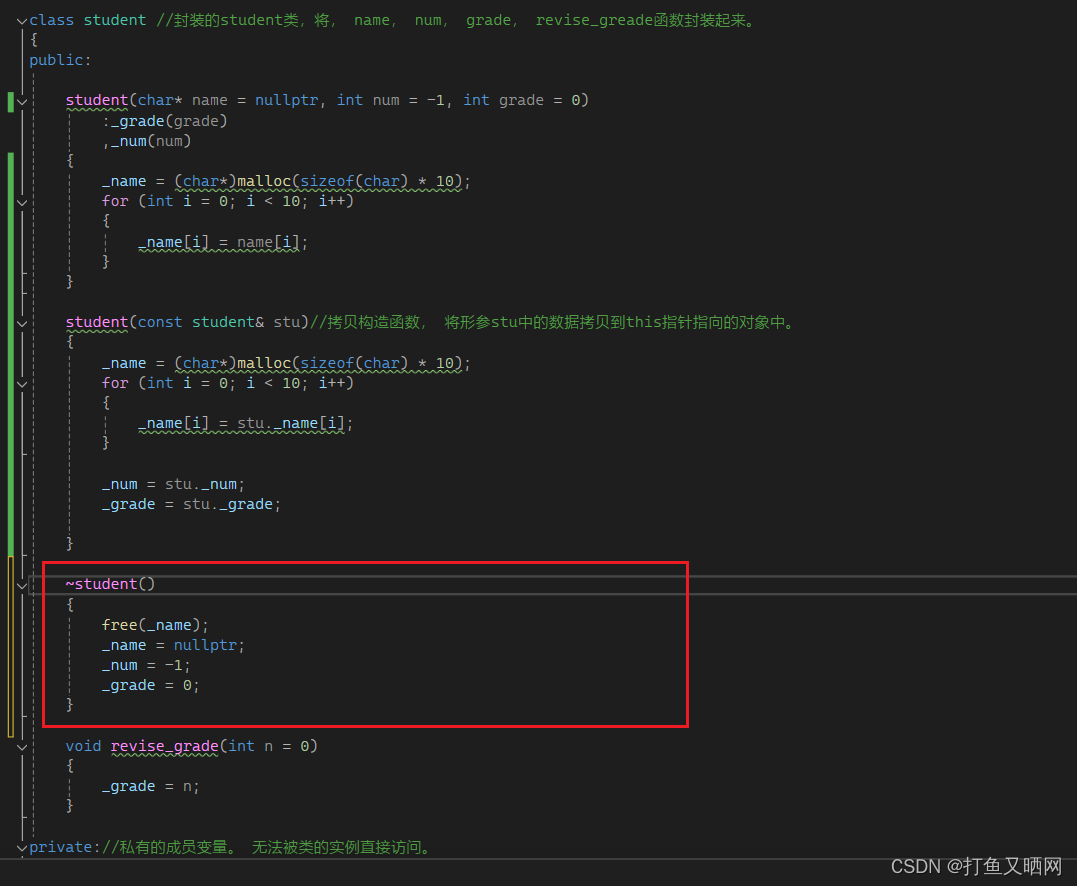
深入学习默认成员函数——c++指南
前言:类和对象是面向对象语言的重要概念。 c身为一门既面向过程,又面向对象的语言。 想要学习c, 首先同样要先了解类和对象。 本节就类和对象的几种构造函数相关内容进行深入的解析。 目录 类和对象的基本概念 封装 类域和类体 访问限定符…...

psutil, 一个超级有用的Python库
Python的psutil是一个跨平台的库,可以用于获取系统运行时的各种信息,包括CPU使用率、内存使用情况、磁盘和网络信息等。它主要用来做系统监控,性能分析,进程管理。它实现了同等命令行工具提供的功能,如ps、top、lsof、…...

[Python]`threading.local`创建线程本地数据
在Python中,threading.local是一个用于创建线程本地数据的工具。它允许每个线程拥有自己独立的变量副本,这样可以在多线程程序中避免共享变量带来的问题。 通过使用threading.local,你可以为每个线程创建一个独立的变量空间,这样…...

删除数据表
oracle从入门到总裁:https://blog.csdn.net/weixin_67859959/article/details/135209645 删除数据表属于数据库对象的操作 drop table 表名称; 删除 emp30 表 SQL> drop table emp30;表已删除。 上面这个语句运行后,就会把数据表 emp30 删除 在…...

前端自带的base64转化方法
前端html的base64使用方法window.btoa()和window.atob()_html用window.btoa();-CSDN博客...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
