数据结构·复杂度
目录
1 时间复杂度
2 大O渐进表示法
举例子(计算时间复杂度为多少)
3 空间复杂度
前言:复杂度分为时间复杂度和空间复杂度,两者是不同维度的,所以比较不会放在一起比较,但是时间复杂度和空间复杂度是用来衡量一个算法是否好坏的标准,时间复杂度用来描述算法运行的时间快慢,空间复杂度用来衡量一个算法所需要的额外空间。最初的计算机时代计算机的存储量很小,所以额外注重空间复杂度,随着发展,计算机的存储已经不是让人担心的点了,所以更为注重时间复杂度。
1 时间复杂度
时间复杂度的定义上可以认为使劲按复杂度是一个函数,定量的描述了算法所需要的时间,但是理论上来说,运行的时间是要上机测试才能测试出来的,实际测试就会花很多时间,所以有了时间复杂度这个分析方式分析算法中执行的基本操作的次数,认定为时间复杂度。
int main()
{for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){//测试语句}}for (int i = 0; i < N; i++){//测试语句}int M = 10;while (M--){//测试语句}return 0;
}这段代码的时间复杂度是?
两个嵌套的for循环,也就是执行了N^2次,再来一个for循环,执行次数为N,最后while收尾,执行次数为10,所以时间复杂度的函数为F(N) = N^2 + N + 10,随着N的增大,式子的值会大到无法想象 ,这都得益于N^2,那么整个式子的决定性因素是N^2,所以我们就认为时间复杂度是N^2。
这种估算的方法被称为大O渐进表示法,只取式子中的决定性因素。
2 大O渐进表示法
计算时间复杂度的时候我们通常采用大O渐进表示法,推导大O阶的表示方法为:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
这里其实完全可以类比高中的数学函数,y = x,x可以是2x也可以是3x,这就是为什么舍弃常数的原因,x和2x是没有区别的。
那么什么是加法常数呢?只要没有循环或者递归,我们都可以认为执行次数为O(1),哪怕是写了一万行代码。
执行程序的时候会存在最好情况 最坏情况 以及平均情况(期望值),一般计算时间复杂度的时候都是计算的最坏情况,所以像冒泡排序,运气好点,时间复杂度就是O(1),运气不好就是O(N^2)了。
举例子(计算时间复杂度为多少)
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N; k++){count++;}int M = 10;while (M--){count++;}printf("%d ", count);
}第一个for循环的执行次数为2 * N次,第二个while循环执行次数为10次,那么函数表达式就是2*N + 10,根据大O表示法,时间复杂度为O(N)。
void Fun3(int N, int M)
{int count = 0;for (int k = 0; k < M; k++){count++;}for (int k = 0; k < N; k++){count++;}printf("%d ", count);
}第一个for循环执行次数为M次,第二个for循环的执行次数为N次,那么函数表达式就是O(M + N),
那么最后结果视结果而定,如果M远大于N,那么时间复杂度就是O(M),那么N >> M同理可得。
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; k++){count++;}printf("%d", count);
}根据第一个for循环的循环条件,循环次数为100次,是常数,所以时间复杂度就是O(1)。
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; end--){int flag = 0;for (size_t i = 1; i < end; i++){if (a[i - 1] > a[i]){swap(&a[i - 1], &a[i]);flag = 1;}}if (flag == 0){break;}}
}冒泡排序严格意义上来说不是标准的O(N^2),因为它的执行次数在随着程序的执行是逐渐减少的,最开始两两比较的次数是N- 1,每趟下来,就会确定一个数据的位置,所以两两比较的次数每次都会减去1,那么if这个语句执行的次数就是N - 1 N - 2……1,利用高中的等差数列的知识,可以得到时间复杂度的函数是F(N) = (N - 1) * (N - 1 + 1) / 2,根据大O表示法,可得得出复杂度为O(N^2)。
int BinarySeatch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;//[begin,end]是查找区间while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid - 1;elsereturn mid;}return -1;
}
这是一个典型的二分查,时间复杂度为直接看是看不出来的,所以有的代码计算时间复杂度是要结合画图的:
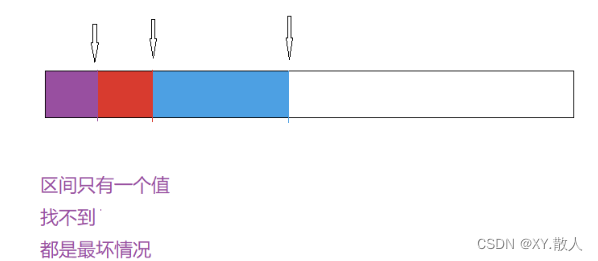
我们讨论最坏情况,二分查找的本质就是不断的缩小区间,一半一半的缩短,那么最开始有N个值,就有N/2/2/2/2/2/2……= 1,那么执行次数就是找的次数就是除以2的次数,计算方式就是
N = 2^x,x是执行的次数,我们求的就是x的值,那么利用高中的换底公式,我们可以得到
x是以2为底,N的对数,而因为对数不太好写,除非使用专业的公式编辑器,所以默认规定LogN,表示的就是以2为底,N的对数,如果有其他底数,就照常写。
long long Fac(size_t N)
{if (0 == N){return 1;}return Fac(N - 1) * N;
}
计算阶乘递归的时间复杂度,递归,会多次开辟函数栈帧,所以一次递归,就会开辟一个函数栈帧,执行次数是1,那么递归n次,总执行次数就是N,所以时间复杂度就是O(N)。
引申:
long long Fac(size_t N)
{if (0 == N)return 1;for (int i = 0; i < N; i++){//测试语句}return Fac(N - 1) * N;
}
递归函数里面加了一个for循环,时间复杂度是多少呢?
不加for循环之前,每个函数的时间复杂度是O(1),开辟了N个函数,那么复杂度就是O(N),但是现在每个函数的时间复杂度就是O(N)了,因为每个子函数里面都有一个for循环,所以N个O(N)的函数放在一起,时间复杂度就是O(N ^ 2)。
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
我们知道递归用来计算斐波那契数列是非常不划算的,因为重复计算的次数太多了,是次方级别的重复:
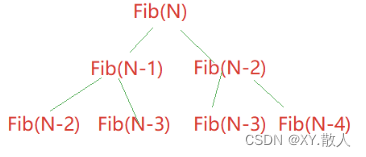
像这样,函数执行的次数是从2的0次方开始,一直到2的N次方,那么利用高中的等比数列的公式,可以得出时间复杂度为函数为F(N) = 2^N - 1,所以时间复杂度就是O(2 ^ N)。
这是非常恐怖的,所以计算斐波那契数列的话还是使用迭代吧!
3 空间复杂度
时间复杂度可以理解为语句的执行次数,空间复杂度可以理解额外开辟的空间,也是采用的大O渐进表示法。当然,空间复杂度不是多少字节,意义不大,因为当前的计算机存储足够大,所以空间复杂度表示的是变量的个数,需要注意的是:函数需要的栈空间在编译期间就已经确定好了,所以计算空间复杂度靠的是程序运行时候显示出来的额外空间。
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; end--){int flag = 0;for (size_t i = 1; i < end; i++){if (a[i - 1] > a[i]){swap(&a[i - 1], &a[i]);flag = 1;}}if (flag == 0){break;}}
}计算冒泡排序的空间复杂度:
这个函数里面有变量,但是是有限个的,如end flag i ,并没有额外开辟空间,所以空间复杂度是O(1),毕竟是没有额外申请空间的。
那么递归计算斐波那契数列的空间复杂度是多少呢?
在此之前我们先看这串代码:
void Test1()
{int a = 10;printf("%p\n", &a);
}
void Test2()
{int b = 10;printf("%p\n", &b);
}
int main()
{Test1();Test2();return 0;
}试问运行结果是不是一样的?有人就会问了,不同函数存的地址肯定不是一样的啊,一般情况是这样的,但是如果两个函数连续调用,并且函数的功能一样,对空间的需求是一样的,那么内存在栈上的空间分配就不会额外开辟空间,也就是说一个函数调用完后,另一个函数就会接着使用这块空间,所以地址是一样的。
那么类比到斐波那契数列的重复计算里面:
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
实际上上开辟的空间都是为了计算函数Fib(N)到Fib(1)的,函数的功能是一样,对空间的需求也是一样的,所以重复计算的时候就不会单独开辟空间,所以需要计算的,都用了开辟的Fib(N)到Fib(1)的空间,那么空间复杂度就是O(N)。
感谢阅读!
相关文章:

数据结构·复杂度
目录 1 时间复杂度 2 大O渐进表示法 举例子(计算时间复杂度为多少) 3 空间复杂度 前言:复杂度分为时间复杂度和空间复杂度,两者是不同维度的,所以比较不会放在一起比较,但是时间复杂度和空间复杂度是用…...

数学建模理论与实践国防科大版
目录 1.数学建模概论 2.生活中的数学建模 2.1.行走步长问题 2.2.雨中行走问题 2.3.抽奖策略 2.4.《非诚勿扰》女生的“最优选择” 3.集体决策模型 3.1.简单多数规则 3.2.Borda数规则 3.3.群体决策模型公理和阿罗定理 1.数学建模概论 1.数学模型的概念 2.数学建模的概…...
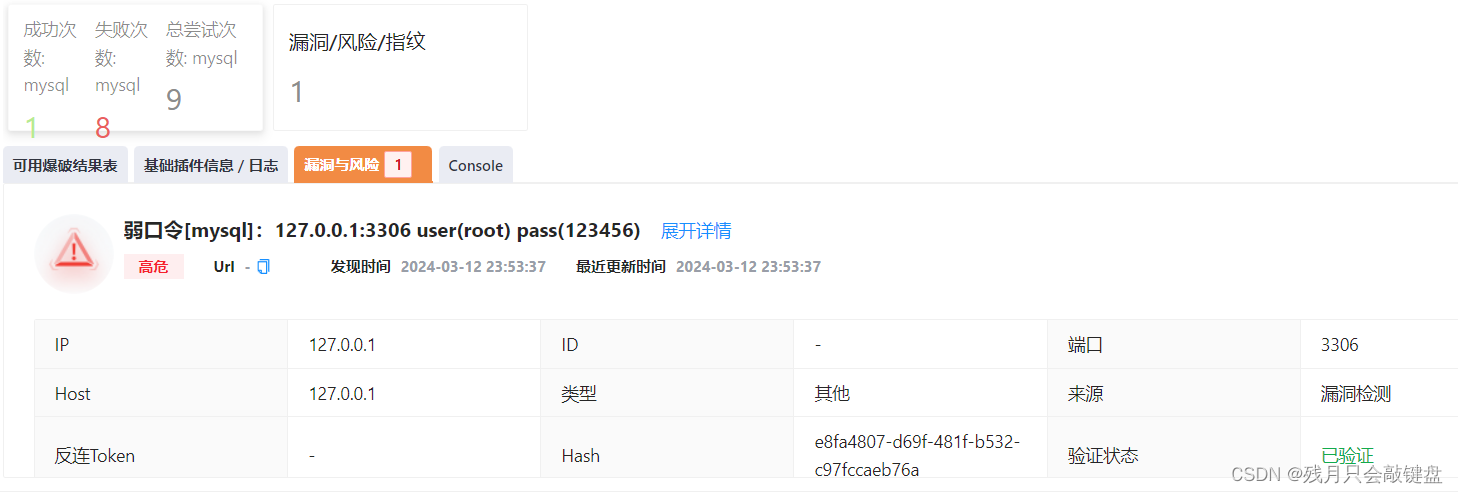
Yakit爆破模块应用
yakit介绍 一款集成了各种渗透测试功能的集成软件。(类似于burp,但我感觉他功能挺强大) 爆破模块位置 按照下面图标点击 界面就是如下。 左侧可以选择爆破的类型,各种数据库http,ssh等都支持。 爆破参数 可以选择…...
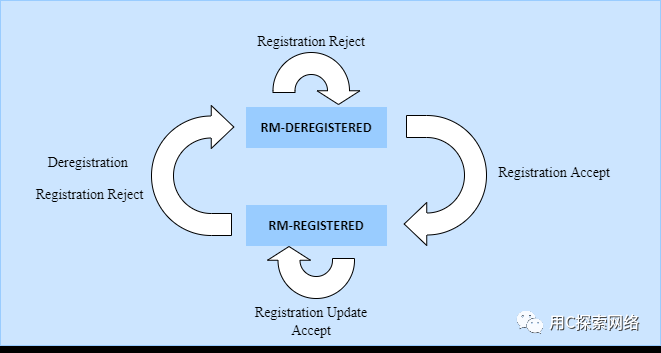
【3GPP】【核心网】【5G】NAS连接管理和UE注册管理状态(超详细)
1. NAS连接管理 NAS连接管理包括通过N1接口在UE和AMF之间建立和释放NAS信令连接的功能。NAS信令连接用于实现UE与核心网络之间的NAS信令交换。当UE接入5G网络时,首先与基站建立RRC连接,当RRC连接建立完成后,UE与基站的空口连接成功建立。随后…...

细粒度IP定位参文2(Corr-SLG):A street-level IP geolocation method (2021年)
[2]S. Ding, F. Zhao, and X. Luo, “A street-level IP geolocation method based on delay-distance correlation and multilayered common routers,” Secur. Commun. Netw., vol. 2021, no. 1, pp. 1–10, 2021. 智能设备的地理位置可以帮助提供多媒体内容提供商和5G网络中…...
Mac上使用M1或M2芯片的设备安装Node.js时遇到一些问题,比如卡顿或性能问题
对于Mac上使用M1或M2芯片的设备可能会遇到在安装Node.js时遇到一些问题,比如卡顿或性能问题。这可能是因为某些软件包或工具在M1或M2芯片上的兼容性不佳。为了解决这个问题,您可以尝试以下方法: 1. 使用Rosetta模式 对于一些尚未适配M1或M2…...

学习vue3第四节(ref以及ref相关api)
主要记录以下api:ref()、isRef()、unref()、 shallowRef()、triggerRef()、customRef() 1、ref() 定义 接受一个内部值,返回一个响应式的、可更改的 ref 对象,此对象只有一个指向其内部值的属性 .value,.value属性用于追踪并且存…...

关于电脑无法开启5G频段热点的解决方案
tips:本文是本着解决校园网开热点后限速的问题的目的,具体情况具体对待。 1.找到设备管理器 右键该选项 2.在新弹出窗口选择首选频带 3.选择首选5GHz频带 确定之后重新连接wifi,重新开启热点,大功告成。 后记:在使用2.4ghz开热点…...
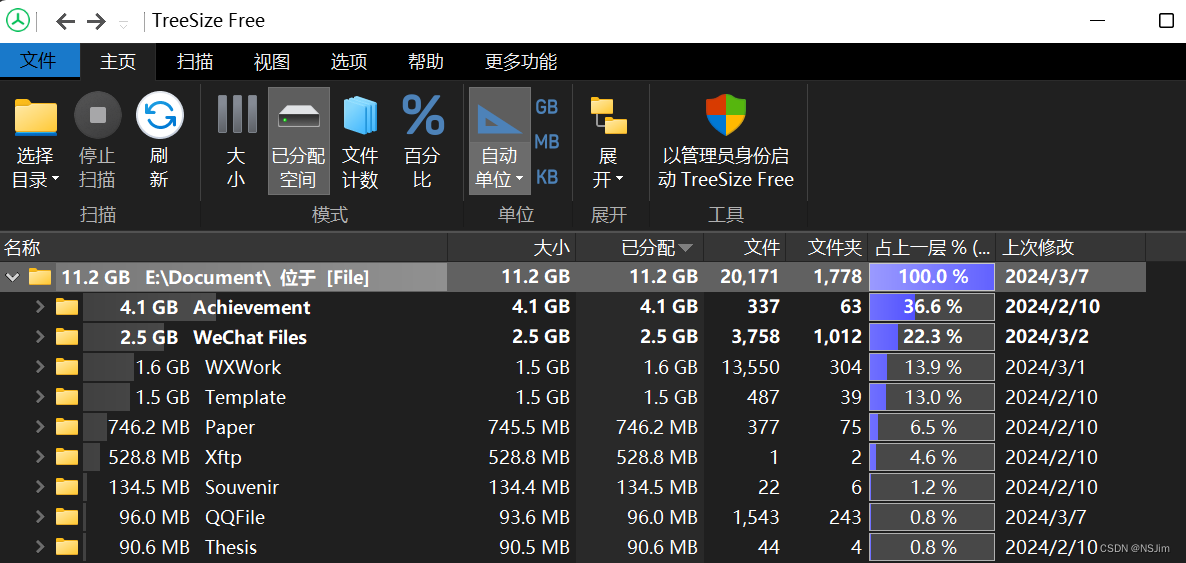
清理磁盘空间 - Win系统
清理磁盘空间 - Win系统 前言系统方案TreeSize FreeSpaceSniffer 前言 我们在使用电脑时经常会出现硬盘空间不足的情况,下文介绍如何清理磁盘空间,包含系统方案、TreeSize Free和SpaceSniffer。清理Window更新等系统文件推荐使用系统方案,清…...

科技革新的引擎-2024年AI辅助研发趋势
随着科技的飞速发展,人工智能(AI)已经在许多领域展现出了其强大的潜力和价值。特别是在研发领域,AI的辅助作用日益凸显,成为推动科技革新的重要引擎。在2024年,这种趋势将更加明显,我们可以从以…...
第四天)
【PTA】L1-021 L1-022 L1-023 L1-024 L1-025(C)第四天
目录 L1-021 重要的话说三遍 题解: L1-022 奇偶分家 题解: L1-023 输出GPLT 题解: L1-024 后天 题解: L1-025 正整数AB 题解: L1-021 重要的话说三遍 分数 5 作者 陈越 单位 浙江大学 这道超级简单的题目没…...

Stable Diffusion 如何写好提示词(Prompt)
本文收录于《AI绘画从入门到精通》专栏,专栏总目录:点这里。 大家好,我是水滴~~ 本文深入探讨了如何撰写出优质的提示词,内容涵盖多个维度:提示词的多样化分类、模型应用中的经典提示词案例、提供丰富资源的提示词参考…...

树莓派Py程序加入开机自启
创建服务文件 为你的服务创建一个 .service 文件。这个文件通常位于 /etc/systemd/system/ 目录下。例如,如果你的服务名称为 my_python_script.service: sudo nano /etc/systemd/system/my_python_script.service 在打开的编辑器中,输入以下…...

Java EasyExcel注解详解和实战案例
文章目录 前言一、导入依赖二、基础知识1. @ExcelProperty1.1 作用1.2 注解参数1.3 示例2. @ExcelIgnore2.1 作用2.2 示例3. @ExcelIgnoreUnannotated3.1 作用3.2 示例4. DateTimeFormat...
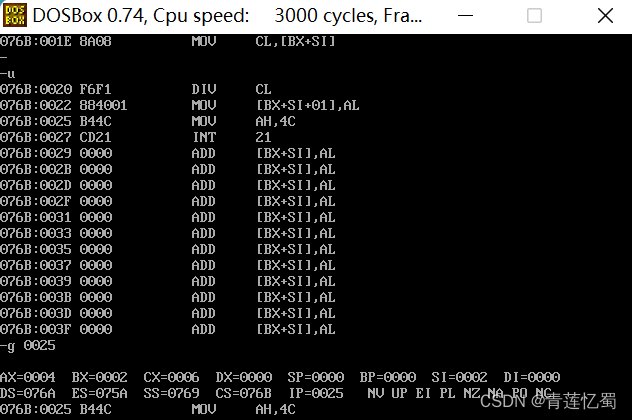
AHU 汇编 实验二
一、实验名称:实验二 不同寻址方式的灵活运用 二、实验内容:定义数组a[6],用多种寻址方式访问对应元素,实现(a[0]a[1])*(a[2]-a[3])/a[4],将结果保存在内存a[5]中,用debug查询结果。 实验过程&a…...
Spring Boot单元测试与热部署简析
1 Spring Boot的简介 Spring Boot是一个用于构建独立的、生产级别的Spring应用程序的框架。它简化了Spring应用程序的开发过程,提供了自动配置和默认配置,使得开发者只需专注于业务逻辑的实现,而不用去关注繁琐的配置问题。 Spring …...

3.12练习题解
1.台阶问题: 这道题目一看其实很容易想到可以用dp的板子去做,并且只需要用一维dp即可,其中dp的下标表示到达当前阶梯总共有多少种方法,由于结果有可能会很大所以一定要记得边记录边模,代码实现如下: #incl…...

Java中实现双向链表
一、目标 最近项目中实现双向链表,同时转为满二叉树。 二、代码 用java实现双向链表的代码如下: class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) { val x; } }public class FullBinaryTree {public TreeNode createTree(int[…...

【DevOps实战之k8s】使用Prometheus和Grafana监控K8S集群
【DevOps实战之k8s】使用Prometheus和Grafana监控K8S集群 目录 【DevOps实战之k8s】使用Prometheus和Grafana监控K8S集群系统架构Kubernetes集群指标抓取指标可视化警告PromQL示例按命名空间统计集群中的Pod数按命名空间重启Pod未就绪的PodCPU过度使用Memory过度使用健康的集群…...

【读论文】【精读】3D Gaussian Splatting for Real-Time Radiance Field Rendering
文章目录 1. What:2. Why:3. How:3.1 Real-time rendering3.2 Adaptive Control of Gaussians3.3 Differentiable 3D Gaussian splatting 4. Self-thoughts 1. What: What kind of thing is this article going to do (from the a…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...
