python】jupyter notebook导出pdf和pdf不显示中文问题
安装nbconvert
首先安装nbconvert才能将.ipynb文件转化为pdf、latex、html等。
conda install nbconvert
安装Pandoc
Pandoc官网下载地址: https://pandoc.org/installing.html
下载安装包github地址:https://github.com/jgm/pandoc/releases/tag/3.1.6.2
安装MiKTex
下载MiKTex: https://miktex.org/download,并将安装的Miktex的安装路径添加到环境变量中。
Miktex的安装路径: F:\MiKTeX\MiKTeX\miktex\bin\x64
否则会报错“nbconvert failed: xelatex not found on PATH……”
输出pdf
安装完Pandoc和MiKTex就可以输出pdf了:
jupyter nbconvert --to latex ./yourfile.ipynb
如果输出的pdf不显示中文
相关文章:

python】jupyter notebook导出pdf和pdf不显示中文问题
安装nbconvert 首先安装nbconvert才能将.ipynb文件转化为pdf、latex、html等。 conda install nbconvert安装Pandoc Pandoc官网下载地址: https://pandoc.org/installing.html 下载安装包github地址:https://github.com/jgm/pandoc/releases/tag/3.1.6.2 安装MiKTex 下载…...

通过SDKMAN安装各种版本JDK
文章目录 1. 安装SDKMAN管理器2. 通过SDK管理器安装JDK3. 参考链接 1. 安装SDKMAN管理器 安装SDKMAN的脚本为: # 1.1 安装: 如果没有权限可以考虑sudo用户执行; curl -s "https://get.sdkman.io" | bash# 1.2 安装完成后查看版本号 sdk version# 1.3 查看帮助信息 …...

软考高级:软件架构风格概念和例题
作者:明明如月学长, CSDN 博客专家,大厂高级 Java 工程师,《性能优化方法论》作者、《解锁大厂思维:剖析《阿里巴巴Java开发手册》》、《再学经典:《Effective Java》独家解析》专栏作者。 热门文章推荐&am…...

Vue3响应式编程
Vue 3 的响应式系统是其核心特性之一,它允许开发者创建响应式的数据绑定和组件状态管理。在 Vue 3 中,响应式系统得到了显著的改进,提供了更好的性能和更灵活的使用方式。 1. 响应式原理 Vue 3 使用了 Proxy 对象来实现响应式系统ÿ…...
决策树算法优化(一篇文章 理解)
目录 引言 一、决策树的基本概念 二、决策树的构建过程 1 特征选择 2 决策树生成 3 决策树剪枝 三、决策树算法的缺点 1 过拟合问题 2 对噪声敏感 3 缺乏连续变量的处理 4 倾向于选择具有较多类别的特征 四、优化策略 1 集成学习 2 连续变量处理 3 特征选择优化 …...

【C语言步行梯】自定义函数、函数递归详谈
🎯每日努力一点点,技术进步看得见 🏠专栏介绍:【C语言步行梯】专栏用于介绍C语言相关内容,每篇文章将通过图片代码片段网络相关题目的方式编写,欢迎订阅~~ 文章目录 什么是函数库函数自定义函数函数执行示例…...

小米汽车上市进入倒计时,已开启内部试驾
在十四届全国人大二次会议上,全国人大代表、小米集团创始人、董事长CEO雷军回应了小米汽车的最新消息,小米汽车预计很快就要正式上市。 小米汽车推出了两款车型:SU7和SU7 Max。这两款车型均为纯电轿车,带来了不同的配置和性能特点…...

React render方法的原理?在什么时候会被触发?
一、原理 首先,render函数在react中有两种形式: 在类组件中,指的是render方法: class Foo extends React.Component {render() {return <div> Foo </div>;} } 在函数组件中,指的是函数组件本身&#x…...

打卡学习kubernetes——了解kubernetes组成及架构
目录 1 什么是kubernetes 2 kubernetes组件 3 kubernetes架构 1 什么是kubernetes kubernetes是一个旨在自动部署、扩展和运行应用容器的开源平台。目标是构建一个生态系统,提供组件和工具以减轻在公共和私有云中运行应用程序的负担。 kubernetes是:…...

python(ogr)处理geojson为本地shp文件
前言 本次所利用的geojson数据来自https://geo.datav.aliyun.com/areas_v3/bound/410000_full.json ,如果觉得下方代码看起来不方便,可以来GitHub上来看,在这上面还有一些辅助内容便于理解 GISpjd/GIS-union-Python (github.com)https://gi…...
Docker容器化技术(使用Dockerfile制作镜像)
Docker中的镜像分层 Docker 支持通过扩展现有镜像,创建新的镜像。实际上,Docker Hub 中 99% 的镜像都是通过在 base 镜像中安装和配置需要的软件构建出来的。 1、Docker 镜像为什么分层 镜像分层最大的一个好处就是共享资源。 比如说有多个镜像都从相…...

C++ struct 结构体类型
在处理大批量数据时,一般会使用数组来实现,数组中各元素都属于同一数据类型。但在实际问题中,要处理的一组数据往往具有不同的数据类型。如一个学生的个人信息有学号(num)、姓名(name)、性别&am…...

什么是VR虚拟现实体验店|VR主题馆加盟|元宇宙文化旅游
VR虚拟现实体验店是一种提供虚拟现实技术体验的场所。在这样的店铺里,顾客可以通过专业的设备和技术,体验虚拟现实技术带来的沉浸式感觉。 通常,这些商店提供一系列VR体验,包括互动游戏、沉浸式模拟、虚拟旅游和其他VR内容。客户可…...
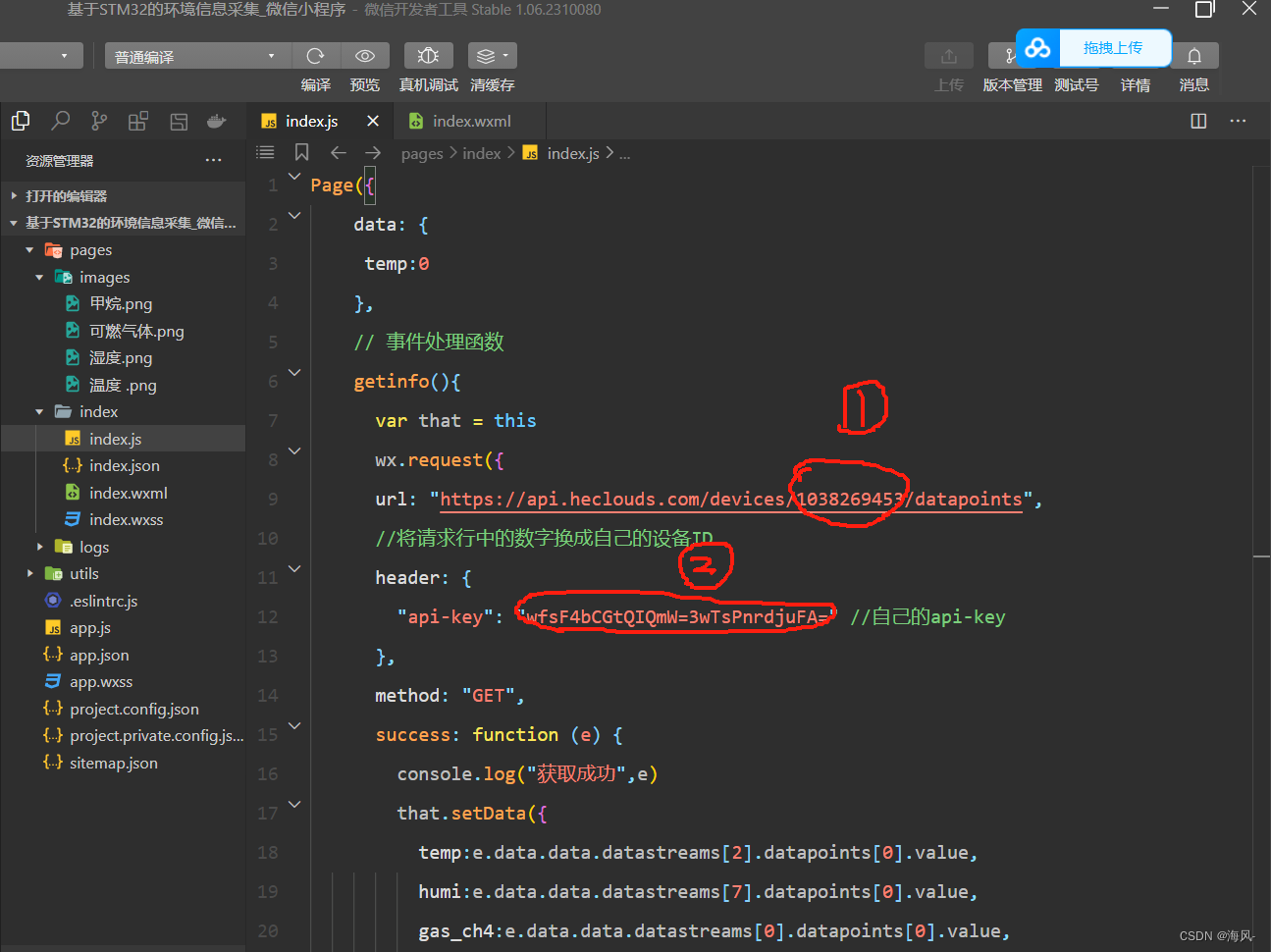
【智能家居入门1之环境信息监测】(STM32、ONENET云平台、微信小程序、HTTP协议)
作为入门本篇只实现微信小程序接收下位机上传的数据,之后会持续发布如下项目:①可以实现微信小程序控制下位机动作,真正意义上的智能家居;②将网络通讯协议换成MQTT协议再实现上述功能,此时的服务器也不再是ONENET&…...
)
AIGC安全研究简述(附资料下载)
2023 AIGC技术实践及展望资料合集(29份).zip 2023 AIGC大型语言模型(LLM)实例代码合集.zip 2023大模型与AIGC峰会(公开)PPT汇总(25份).zip AIGC的安全研究是一个复杂且重要的领域,涉及多个关键…...
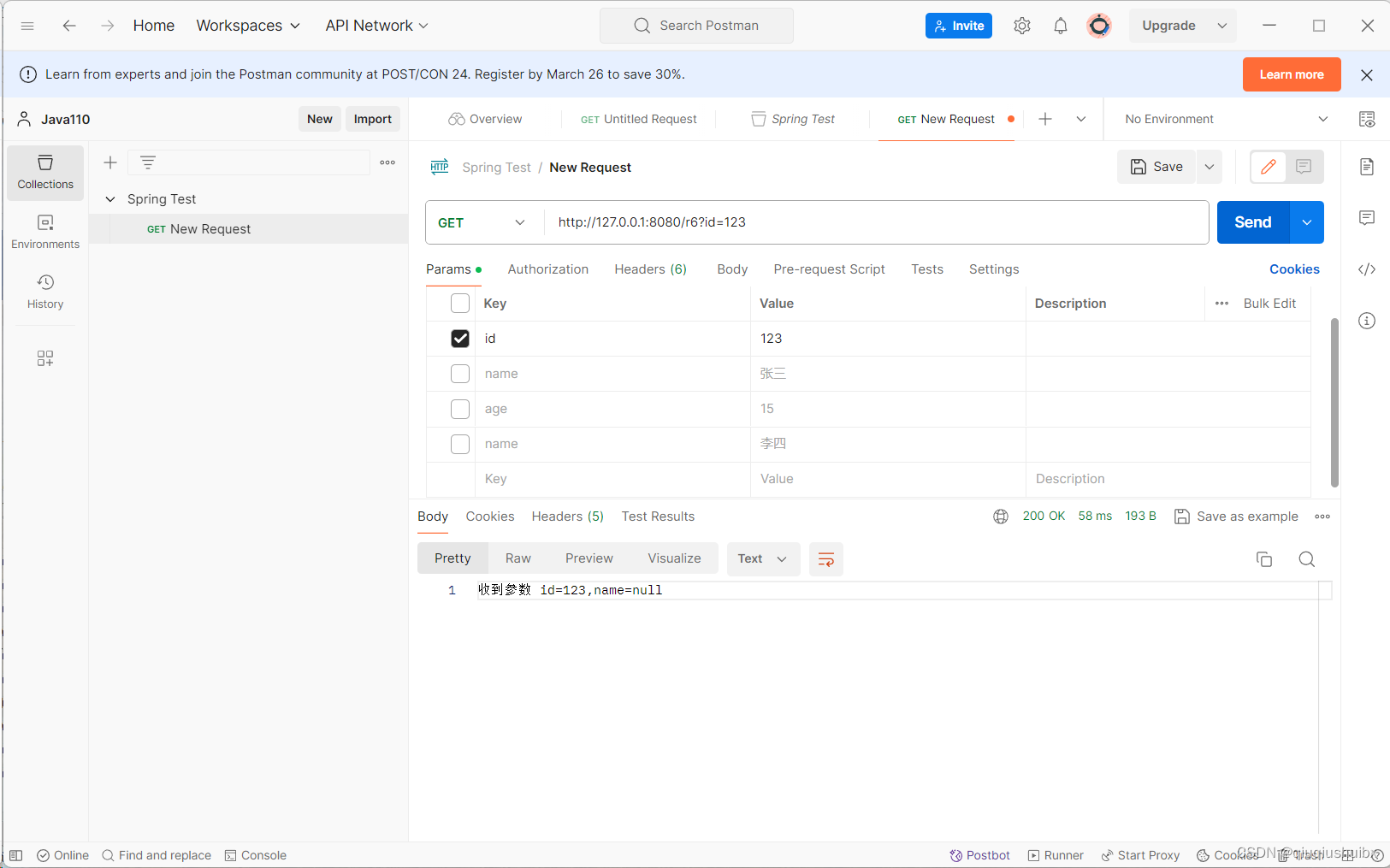
初识Spring MVC
什么是Spring MVC? 官方给的解释是 Spring Web MVC 是基于 Servlet API 构建的原始 Web 框架,从⼀开始就包含在 Spring 框架中。它的 正式名称“Spring Web MVC”来⾃其源模块的名称(Spring-webmvc),但它通常被称为"Spring MVC" 注:Severlet是…...
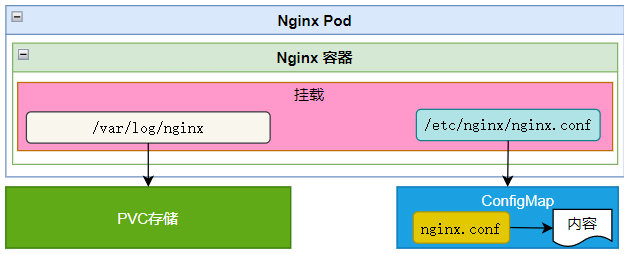
云原生之容器编排实践-ruoyi-cloud项目部署到K8S:Nginx1.25.3
背景 前面搭建好了 Kubernetes 集群与私有镜像仓库,终于要进入服务编排的实践环节了。本系列拿 ruoyi-cloud 项目进行练手,按照 MySQL , Nacos , Redis , Nginx , Gateway , Auth ,…...
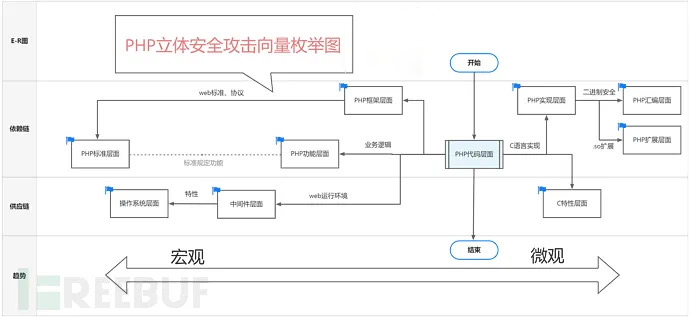
PHP立体安全攻击向量:保护应用程序的关键挑战
PHP立体安全攻击向量:保护应用程序的关键挑战 PHP作为一种广泛使用的服务器端脚本语言,拥有庞大的用户群体和丰富的生态系统。然而,随着互联网的发展,网络安全问题也变得愈发严重。本文将深入探讨PHP的立体安全攻击向量࿰…...
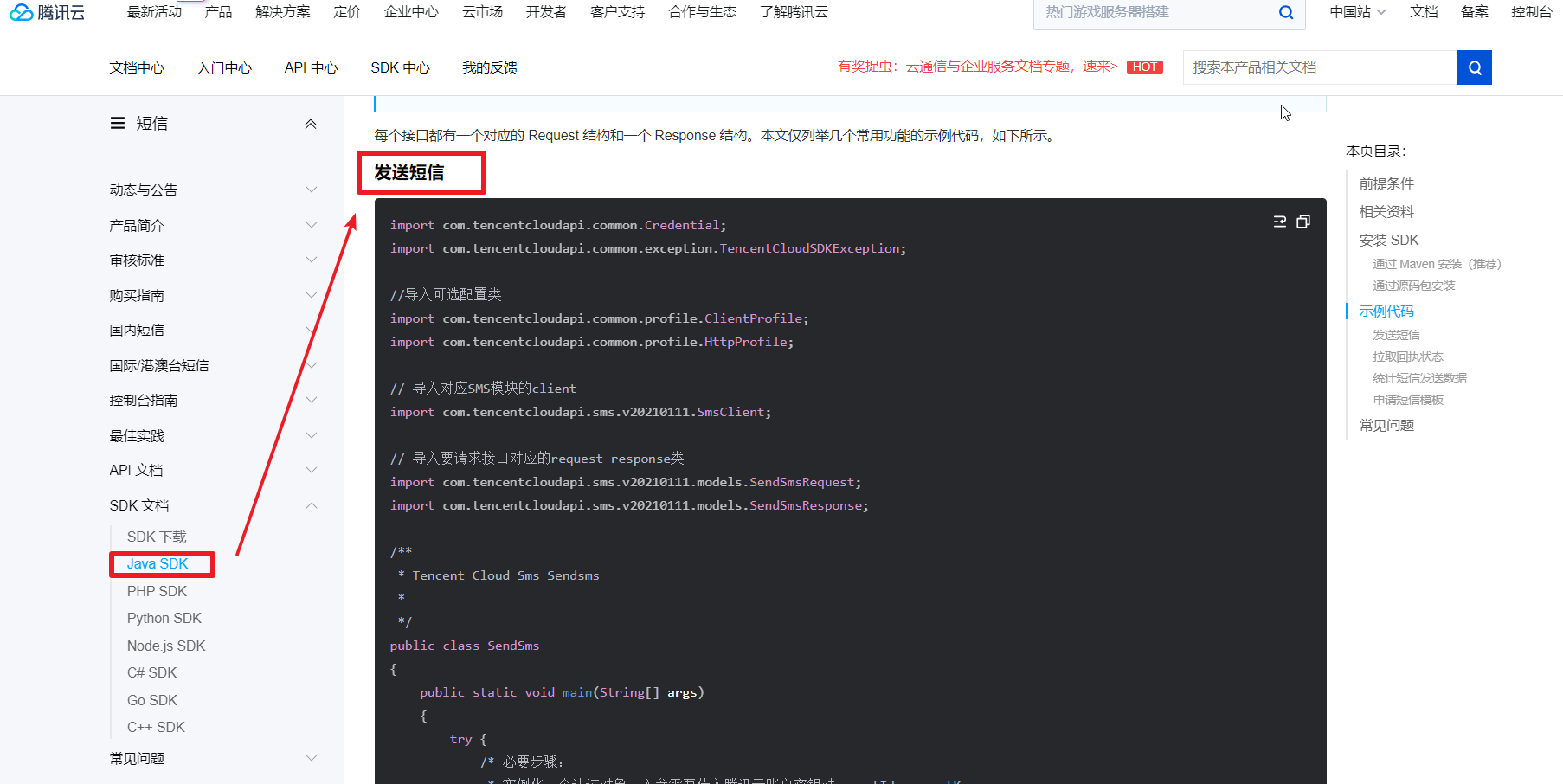
【功能大全】手机短信验证码一键注册登录流程
目录 发送验证码 注册登录 用户表设计 编辑申请腾讯云短信与密钥 找到云短信服务 开通腾讯云短信服务 编辑创建短信签名 编辑编辑创建短信正文模版编辑编辑 等待审核 测试短信编辑 SDK密钥创建 SpringBoot集成腾讯云短信 pom中导入腾讯云短…...

【Python】【Matplotlib】深入解析plt.grid()---原理、应用与注意事项
【Python】【Matplotlib】深入解析plt.grid()—原理、应用、源码与注意事项 🌈 个人主页:高斯小哥 🔥 高质量专栏:Matplotlib之旅:零基础精通数据可视化、Python基础【高质量合集】、PyTorch零基础入门教程Ǵ…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...

【大厂机试题解法笔记】矩阵匹配
题目 从一个 N * M(N ≤ M)的矩阵中选出 N 个数,任意两个数字不能在同一行或同一列,求选出来的 N 个数中第 K 大的数字的最小值是多少。 输入描述 输入矩阵要求:1 ≤ K ≤ N ≤ M ≤ 150 输入格式 N M K N*M矩阵 输…...
