算法训练day42leetcode01背包问题 416. 分割等和子集
01 背包
题目描述
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
题目分析
每一件物品其实只有两个状态,取或者不取,所以可以使用回溯法搜索出所有的情况,那么时间复杂度就是$o(2^n)$,这里的n表示物品数量。
所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化!
- 确定递推公式
再回顾一下dp[i][j]的含义:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
那么可以有两个方向推出来dp[i][j],
- 不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
- 放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
数据结构:
weight:一个向量,包含各个物品的重量。value:一个向量,包含各个物品的价值。bagweight:一个整数,代表背包的总容量。dp:一个2D向量,其中dp[i][j]表示用前i个物品填充容量为j的背包时可以达到的最大价值。
算法步骤:
- 初始化:首先,使用物品0初始化
dp数组的第一行。如果背包的容量大于等于物品0的重量,则背包可以装下物品0,所以对所有的j >= weight[0],dp[0][j]的值被设置为物品0的价值。 - 填充DP表:接下来,遍历每个物品(除了第一个已经处理过的物品),并对每个可能的背包容量进行考虑。对于每个物品
i和每个容量j:- 如果当前背包容量
j小于物品i的重量,则无法包含当前物品,因此dp[i][j]的值就是不包含当前物品时的最大价值,即dp[i-1][j]。 - 如果当前背包容量可以容纳物品
i,则需要决定是包含还是不包含当前物品以达到最大价值。这通过比较不包含当前物品(dp[i-1][j])和包含当前物品(dp[i-1][j-weight[i]] + value[i])时的价值来决定。选择这两种情况中的最大值作为dp[i][j]的值。
- 如果当前背包容量
输出:
- 通过查看
dp数组的最后一个元素dp[weight.size() - 1][bagweight],可以得到使用给定物品填充指定容量背包的最大价值。
这种动态规划方法有效地解决了0/1背包问题,通过构建一个解决方案的表格,使得可以通过较小的子问题的解来构建出整个问题的解,从而避免了冗余的计算和指数级的复杂度。
acm模式代码
#include <iostream>
#include <vector>
using namespace std;void test_2_wei_bag_problem1() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagweight = 4;// 二维数组vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));// 初始化for (int j = 0 ; j < weight[0]; j++) { // 当然这一步,如果把dp数组预先初始化为0了,这一步就可以省略,但很多同学应该没有想清楚这一点。dp[0][j] = 0;}for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];}// weight数组的大小 就是物品个数for(int i = 1; i < weight.size(); i++) { // 遍历物品for(int j = 0; j <= bagweight; j++) { // 遍历背包容量if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}}cout << dp[weight.size() - 1][bagweight] << endl;
}int main() {test_2_wei_bag_problem1();
}01背包一维
题目分析
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。
这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了。
所以一维dp数组的背包在遍历顺序上和二维其实是有很大差异的!
acm模式代码
#include <iostream>
#include <vector>void test_1_wei_bag_problem() {std::vector<int> weight = {1,3,4};std::vector<int> value = {15, 20 ,30};int bagweight = 4;//初始化std::vector<int> dp(bagweight + 1, 0);for (int i = 0; i < weight.size(); i++) {for (int j = bagweight;j >= weight[i]; j--) {dp[j] = std::max(dp[j], dp[j - weight[i]] + value[i]);}}std::cout << dp[bagweight] << std::endl;
}int main() {test_1_wei_bag_problem();
}416. 分割等和子集
题目描述
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5] 输出:true 解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5] 输出:false 解释:数组不能分割成两个元素和相等的子集。
提示:
1 <= nums.length <= 2001 <= nums[i] <= 100
acm模式代码
#include <iostream>
#include <vector>
using namespace std;class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0;for (int num : nums) {sum += num;}if (sum % 2 != 0) return false; // Early return if the sum is odd.int target = sum / 2;vector<bool> dp(target + 1, false);dp[0] = true; // Base case: zero sum is always possible.for (int num : nums) {for (int j = target; j >= num; j--) {dp[j] = dp[j] || dp[j - num];}}return dp[target];}
};int main() {Solution sol;vector<int> nums = {1, 5, 11, 5}; // Example inputbool canPart = sol.canPartition(nums);if(canPart) {cout << "Can partition: YES" << endl;} else {cout << "Can partition: NO" << endl;}return 0;
}
相关文章:

算法训练day42leetcode01背包问题 416. 分割等和子集
01 背包 题目描述 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 题目分析 每一件物品其实只有两个状态,取或者不取&…...
VulnHub - DarkHole
希望和各位大佬一起学习,如果文章内容有错请多多指正,谢谢! 个人博客链接:CH4SER的个人BLOG – Welcome To Ch4sers Blog DarkHole 靶机下载地址:DarkHole: 1 ~ VulnHub 0x01 信息收集 Nmap扫描目标主机…...

前端学习笔记 | WebAPIs(DOM+BOM)
一、作用和分类 1、基本概念 作用:使用JS去操作HTML和浏览器 分类:DOM(文档对象模型)和BOM(浏览器对象模型) html的标签JS的DOM对象 2、获取DOM对象-参数必须加引号 (1)选择匹配的第…...
C卷(JavaPythonC++Node.jsC语言))
简易内存池(100%用例)C卷(JavaPythonC++Node.jsC语言)
请实现一个简易内存池 , 根据请求命令完成内存分配和释放。 内存池支持两种操作命令,REQUEST和RELEASE,其格式为: REQUEST=请求的内存大小 表示请求分配指定大小内存,如果分配成功,返回分配到的内存首地址;如果内存不足,或指定的大小为 0 ,则输出error。 RELEASE=释放的…...

【算法与数据结构】队列的实现详解
文章目录 📝队列的概念及结构🌠 队列的顺序实现🌉初始化🌠入队🌉出队🌠获取队列首元素🌉获取队列尾部元素🌠获取队列中有效元素个数🌉 队列是否为空🌠查看队列…...

GPT-3后的下一步:大型语言模型的未来方向
摘要: 本文将概述GPT-3后的下一步:大型语言模型的未来方向,包括技术发展趋势、应用场景、挑战与机遇。 引言: GPT-3是OpenAI于2020年发布的一款大型语言模型,它在自然语言处理领域取得了突破性进展。GPT-3的出现标志…...
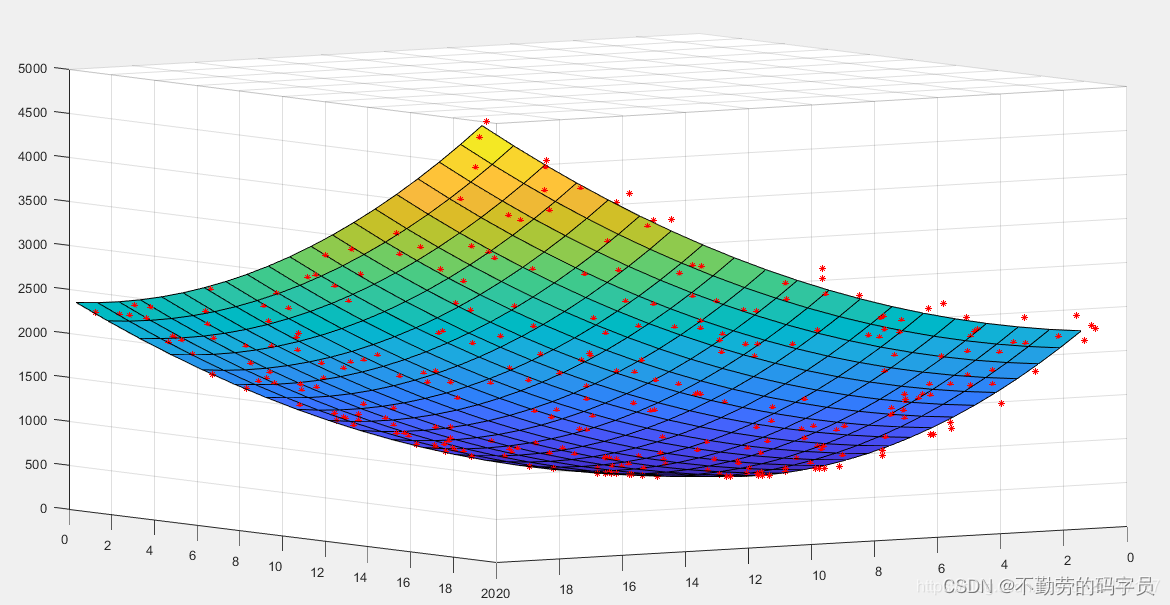
基于机器学习的曲面拟合方法
随着科技的不断发展,机器学习成为了最近最热门的技术之一,也被广泛应用于各个领域。其中,基于机器学习的曲面拟合方法也备受研究者们的关注。曲面拟合是三维模型处理中的重要技术,其目的是用一组数据点拟合出平滑的曲面࿰…...

【C++从练气到飞升】03---构造函数和析构函数
🎈个人主页:库库的里昂 ✨收录专栏:C从练气到飞升 🎉鸟欲高飞先振翅,人求上进先读书。 目录 ⛳️推荐 一、类的6个默认成员函数 二、构造函数 1. 构造函数的概念 2. 构造函数的定义 3. 构造函数的特性 三、析构函…...

mybatis转义字符
编写SQL中会用到<,>,<,> 等,但是在mybatis中不可以这么写,与xml文件的元素<>冲突,所以需要转义。整理转义字符如下: 符号原始字符转义字符大于>>大于等于>>小于<<小于等于<<和&&a…...
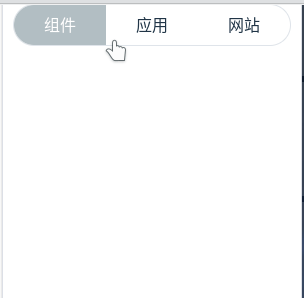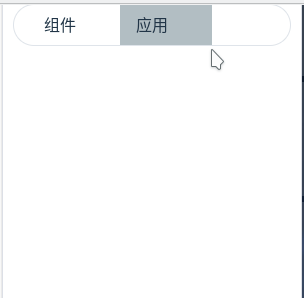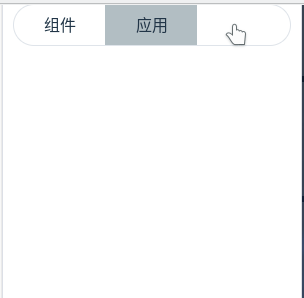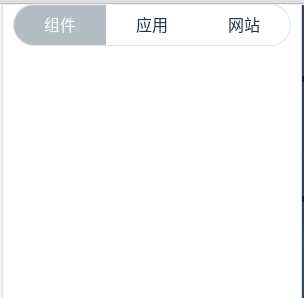
vue3 实现一个tab切换组件
一. 效果图 二. 代码 文件 WqTab.vue: <template><div ref"wqTabs" class"wq-tab"><template v-for"tab in tabs" :key"tab"><div class"tab-item" :class"{ ac: tabActive tab.key }" c…...

JSONObject在Android Main方法中无法实例化问题
目录 前言一、Main(非安卓环境)方法下运行二、安卓坏境下运行三、why? 前言 原生的json,即org.json.JSONObject; 在Android Studio中的Main方法里运行报错,但在安卓程序运行过程正常 一、Main(非安卓环境)方法下运行 static void test() {try {// 创建一个 JSON …...

京津冀协同发展:北京·光子1号金融算力中心——智能科技新高地
京津冀协同发展是党中央在新的历史条件下提出的一项重大国家战略,对于全面推进“五位一体”总体布局,以中国式现代化全面推进强国建设、民族复兴伟业,具有重大现实意义和深远历史意义。随着京津冀协同发展战略的深入推进,区域一体…...

aspnetcore使用jwt时一直提示401 authorization
测试aspnetcore使用Jwt做认证授权的时候,一直提示401 Authorization 最后发现问题所在,希望能有所帮助 1.检查注册了认证和授权中间件 缺一不可 /*认证*/app.UseAuthentication();/*授权*/app.UseAuthorization();2.检查swagger的配置项 builder.Servic…...
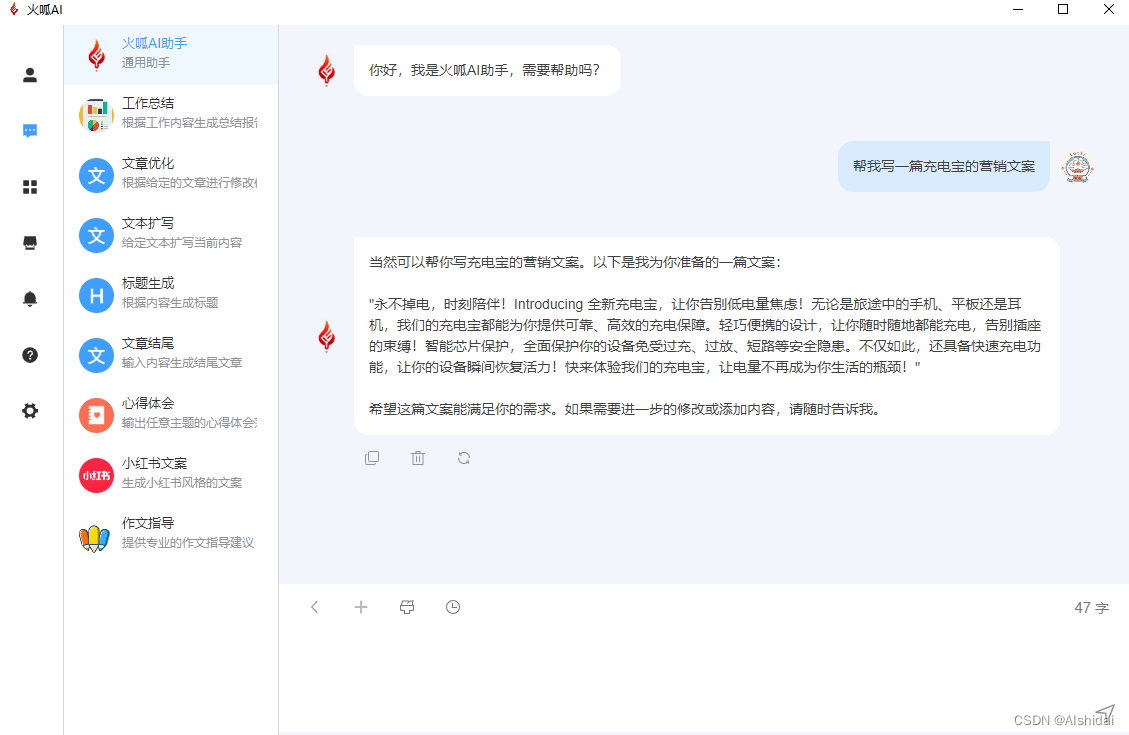
三款文案自动生成器,帮你轻松生成原创文案
文案在今天已经成为了许多企业和个人推广产品和服务的重要手段。然而,对于很多人来说,写作文案并非易事。有时候,我们可能会遇到文案灵感枯竭的情况,或者花费大量时间在寻找合适的词句上。但是,别担心!现在…...

多线程并发模拟实现与分析:基于Scapy的TCP SYN洪水攻击实验研究
简介 实现基于Python实现的多线程TCP SYN洪水攻击。该实例利用Scapy库构造并发送TCP SYN数据包,通过多线程技术模拟并发的网络攻击行为。 实现原理 SYN Flood攻击是一种经典的分布式拒绝服务(DDoS)攻击方式,利用了TCP协议握手过…...
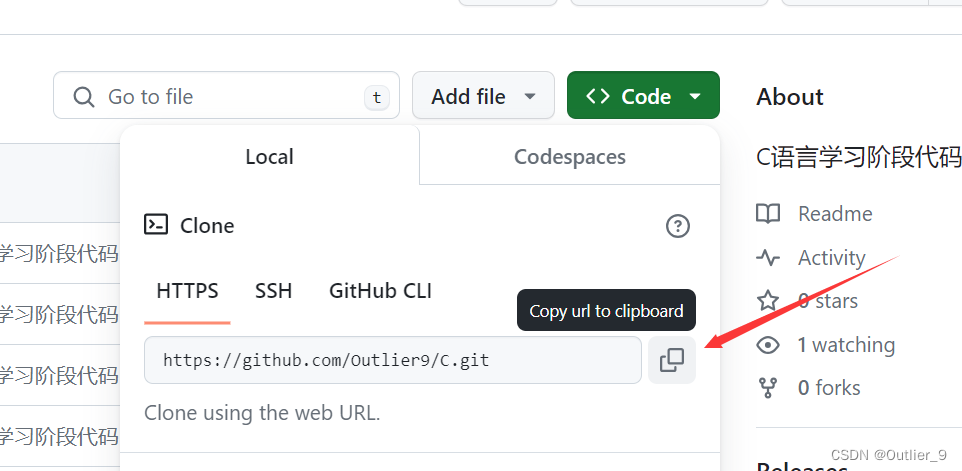
git命令行提交——github
1. 克隆仓库至本地 git clone 右键paste(github仓库地址) cd 仓库路径(进入到仓库内部准备提交文件等操作) 2. 查看main分支 git branch(列出本地仓库中的所有分支) 3. 创建新分支(可省…...
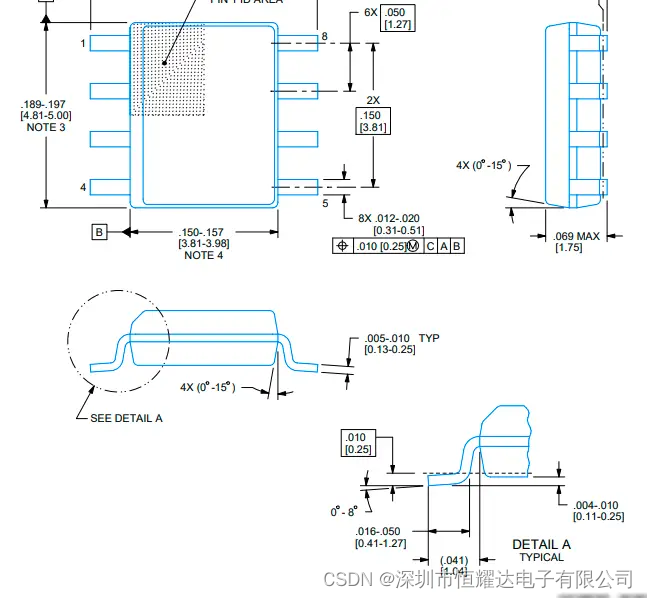
LM2903BIDR比较器芯片中文资料规格书PDF数据手册参数引脚图功能封装尺寸图
产品概述: M393B 和 LM2903B 器件是业界通用 LM393 和 LM2903 比较器系列的下一代版本。下一代 B 版本比较器具有更低的失调电压、更高的电源电压能力、更低的电源电流、更低的输入偏置电流和更低的传播延迟,并通过专用 ESD 钳位提高了 2kV ESD 性能和输…...

遍历list过程中调用remove方法
1、普通for循环遍历List删除指定元素,list.remove(index) List<String> nameList new ArrayList<>(Arrays.asList("张三", "李四", "王五", "赵六")); nameList.add("张七"); nameList.add("…...

Java解决罗马数字转整数
Java解决罗马数字转整数 01 题目 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 …...

无忧·企业文档v2.1.9新版本发布,全新升级,新变化让文档管理更无忧!
项目介绍 JVS是企业级数字化服务构建的基础脚手架,主要解决企业信息化项目交付难、实施效率低、开发成本高的问题,采用微服务配置化的方式,提供了 低代码数据分析物联网的核心能力产品,并构建了协同办公、企业常用的管理工具等&…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...
